量化投资中的聚类、贝叶斯判别及因子分析应用研究
2017-03-20郭洪涛唐灵
郭洪涛,唐灵
(江西师范大学,江西南昌330022)
一、引 言
量化投资在海外的发展已经长达几十年,由于具有投资理性客观,业绩稳定、市场规模和份额不断扩大的特性使其在投资决策方面更容易抓住阿尔法的盈利机会,在投资界逐渐成为决策的重要依据。近年来,聚类分析、判别分析、因子分析在自然科学、社会学及经济管理学科中都有广泛的应用。本文将聚类分析应用到量化投资,可根据某些指标将具有类似特性的股票聚集为一类,便于进一步详细分析及为股票的量化投资作参考,聚类之后本文将贝叶斯判别分析应用于聚类分析结果的检验。对于判别分析,该分析方法利用已知类别的样本建立判别模型,为未知类别的样本进行判别。
二、文献综述
目前,国内外对量化投资的研究日益增多,量化投资学者王力弘曾强调定量投资管理是定性思想的量化应用,强调数据,并且他总结了量化投资的四个特点:纪律性(即靠模型的运行结果预测而非主观臆断)、系统性(即从多层次、多角度、多数据等方面建立模型)、运用套利思想(全面系统地通过扫描捕捉到错误定价、错误估值带来的机会)和概率取胜。量化投资的代表人物詹姆斯·西蒙斯投资股票,曾在17年间年平均收益达到38.5%,特别在次贷危机爆发的年代还能达到回报率为85%。西蒙斯的研究方法可以用三点来概括:在公众市场上交易,首先有足够的流动性,其次用数学模型来交易。
在实际应用中,利用金融投资思维与数学统计方法相结合,借助计算机强大的数据处理分析能力,可快速处理数量模型中各因子间逻辑关系,对各个股票的历史数据同时跟踪与分析研究,扩大投资广度的同时也提高量化投资的效率。
三、理论框架和假设前提
1.聚类分析方法简单介绍
聚类分析,是一种建立分类的多元统计分析方法,是根据一批样本数据的诸多特征,按照在性质上的亲疏程度在没有先验知识的情况下进行自动分类,产生多个分类结果,即按照个体或样品(individuals,objects or subjects)的特征将它们分类,使同一类别内的个体具有尽可能高的同质性(homogeneity),而类别之间则应具有尽可能高的异质性(heterogeneity)。
本文中采用K-Means聚类,即快速聚类,它是以距离作为测度个体“亲疏程度”的指标,并以牺牲多个解为代价换得高的执行效率,其核心步骤为:
第一步:指定聚类数目K,在文中的案例分析中,先指定聚类数目为4,最终K-Means聚类输出关于它的唯一解。
第二步:确定K个初始类中心。
第三步:根据距离最近原则进行分类,依次计算每个样本点到K=4个类中心的欧氏距离,并按照距K=4个类中心点距离最近的原则分派所有样本,形成K=4个分类。
第四步:重新确定K=4个类中心,中心点的确定原则是:依次计算各类中k=4个变量的均值,并以均值点作为K个类的中心点。
第五步:判断是否已满足终止聚类分析的条件。
2.贝叶斯判别分析的简单介绍
贝叶斯(Bayes)判别思想是根据先验概率求出后验概率,并依据后验概率分布作出统计推断。
贝叶斯判别的计算步骤为:
第一:计算先验概率。
第二:计算样本似然。样本似然是指在总体Gi(i=1,2,…,k)中抽到样本X的概率或概率密度,记为 p(X|Gi)。
以两个总体为例。如果判别变量服从多元正态分布,且各总体(类别)的协差矩阵相等,则在总体G1中抽到样本X的概率密度为:

即为多元正态分布的密度函数。其中,|Σ|是协方差的行列式值,称为广义方差。中括号部分为马氏距离D12,于是有:

同理,在总体G2中抽到样本X的概率密度为:

第三:计算样本属于总体 Gi(i=1,2,…,k)的概率 p(Gi|X)。
根据贝叶斯定义,用判别函数的信息调整先验概率,有:
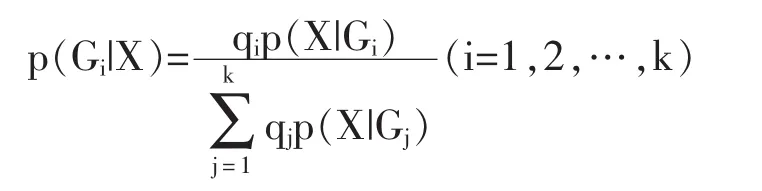

样本X应属于p(Gi|X)最大的类。
此外,要使判别分析的效果较为理想,多个类别总体下的各判别变量的均值应存在显著差异,否则给出错误判别结果的概率会较高。通常,应首先进行总体的均值检验,也就是判断各类别总体下判别变量的组间差是否显著。
SPSS采用方差分析的方法,利用F统计量,对每个判别变量逐个进行检验,同时还计算Wilk’s λ统计量。检验统计量定义为:
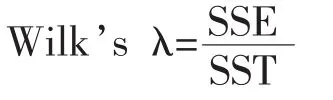
其中,SSE为组内离差平方和,SST为判别变量的总离差平方和。分子反映了组内离差,分母反映了离差。
Wilk’s λ越接近1,说明判别变量的总离差中组内差所占比例越大,各组间均值差异越小。
SPSS将给出Wilk’s λ统计量、F统计量的观测值和对应的概率p值。如果p值小于显著性水平α,则应拒绝原假设,说明各类别总体下,该判别变量的均值显著差异较小,可采用判别分析。
3.因子分析
因子分析产生的因子能够通过各种方式最终获得命名解释性。例如,通过对以上聚类分析的股票组类进行因子分析,如果得到两个因子,且一个因子是净利润同比增长率和营业总收入增长率的综合,而另一个是对净资产收益率摊薄和销售毛利率的综合,那么这种因子分析就是较为理想的。因为这两个因子均有命名可解释性,其中一个反映了一类股票的成长能力情况,可命名为成长能力因子,另一个反映了一类股票的盈利能力情况,可命名为盈利能力因子。
因子分析的核心是用较少的互相独立的因子反映原有变量的绝大部分信息。可以将这一思想用数学模型来表示。设原有p个变量x1,x2,x3,…,xp,且每个变量(或经标准化处理后)的均值为0,标准差均为1。现将每个原有变量用k(k<p)个因子 f1,f2,f3,…,fk,的线性组合来表示,即有:

四、案例分析过程
以下对生物制品板块中32只股票2016年第一季度的财务数据进行分析。
表1是生物制品板块中32只股票研究对象数据指标的处理摘要,从摘要可看出此次案例分析有效数据32个,无缺失值。

表1 案例处理摘要a
首先,设置四个财务指标分别为净资产收益率、销售毛利率、营业收入同比增长率及净利润增长率。其中,在经济学中,从概念上讲,净资产收益率和销售毛利率可用来衡量盈利能力,营业收入同比增长率及净利润增长率可用来衡量成长能力,通过SPSS进行K-Means聚类分析(用系统聚类这种聚类结果判别程度不高,并且后期聚类修正步骤繁琐,笔者用系统聚类得到三组分类方法,分为5组时贝叶斯判别得到判对率为90.6%,分为4组时判对率为93.8%,分为3组时判对率为96.9%,模型的总判对率虽然较高但是后期修正步骤繁琐,所以本文整理出K-Means聚类分析的过程及结果,得到如表2所示输出结果。

表2 聚类成员
由SPSS输出结果可知,生物板块32只股票被分成了4类,并且每类的分布比例为24∶4∶3∶1。在之前聚类分析的结果上,如图1所示,接下来采用贝叶斯判别对生物制品行业32家公司2016年第一季度的财务数据进行判别分析。
以下是判别结果的输出:
表3为贝叶斯判别函数的特征值表,由此表可知2个判别函数的相关性很高,方差的贡献率为88.2%,判别函数较为可靠。相关系数越大,说明该判别函数轴上的类别差异越明显,第一个判别函数最优。

表3 特征值a

表4 Wilks的Lambda
表4是Wilks检验结果,从统计检验角度分析哪个判别函数的判别能力是显著或不显著的,从各判别函数联合判别能力的检验入手,采用反向指标测度。检验的原假设H0:各判别函数的整体判别能力不显著,采用的Wilks’λ统计量,值越小说明整体判别能力越强,当Wilks’λ观测值小于一定显著水平α下的临界值时,则认可判别函数判别能力具有统计显著性。表5表明原假设成立的条件下,该观测值或更极端情况出现的概率,即观测p值为0.00,如果显著水平α为0.05,由于概率p值小于显著性水平α,应拒绝原假设,认为第一和第二判别函数的整体判别能力统计显著。由于第一、第二判别函数的方差贡献度分别为88.2%和11.8%,仍可以考虑略去第二判别函数。

表5 分类结果a
从以上分析可知实际有32只股票,有3只股票被误判,分别是案例号为9、16、26的股票被误判为第二类、第四类、第一类,对判为第一类的正确率为95.8%,对判为第二类、第三类正确率为100%,模型判别的总正确率为90.6%。为了进一步提高模型的总正确率,将9号迈克生物、16号钱江生化、26号上海莱士从第二类、第四类、第一类中分别调到第一类、第二类、第二类中。
为了进一步提高模型的总正确率,将19号ST生化从第二类中调到第一类中,得到第三次聚类结果,此次的聚类结果仍然是三类,各类别的比例为25∶4∶3,对前两次的聚类结果作调整,可看到聚类结果的模型贝叶斯判对的总正确率在逐步提高,由最初的90.6%提高到96.9%,现在依然对这次的聚类结果调整做贝叶斯判别,判对率进一步提高到100%。
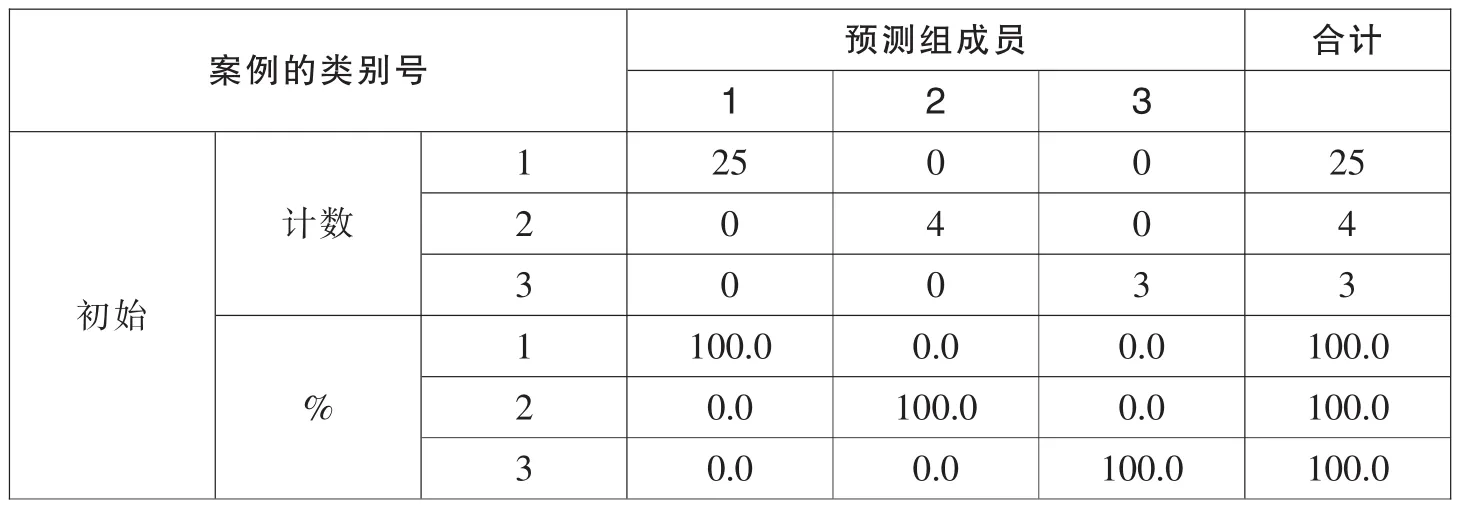
表6 分类结果a
如表6所示的案例分析结果,此次聚类结果的贝叶斯判别分析结果为:实际有32只股票,没有股票被误判,32只股票分为三类,各类别比例为25∶4∶3,对判为第一类的正确率为100%,对判为第二类正确率为100%,对判为第三类的正确率为100%,模型判别的总正确率为100%,显然此次判别效果最准确,说明这个聚类模型的结果最佳。
表7是对此次聚类结果的贝叶斯判别的案例分析结果,下面分别进行详细分析。
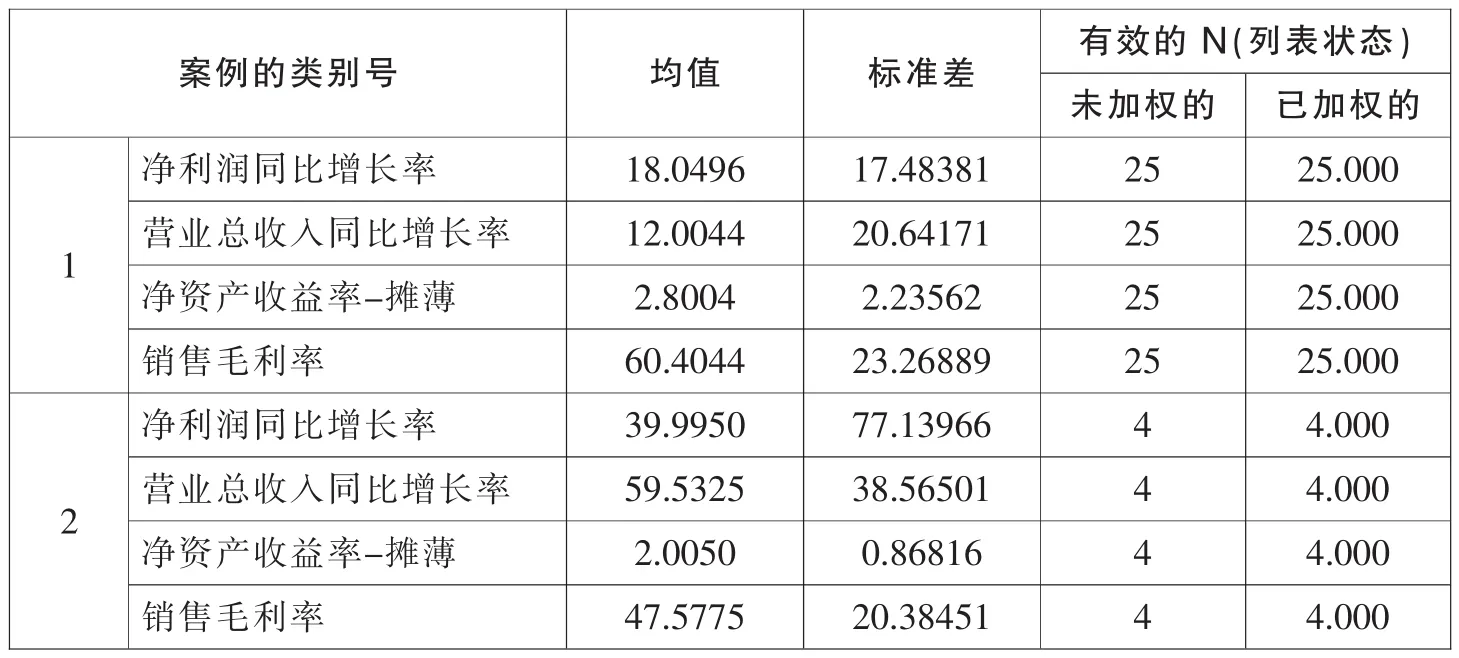
表7 组统计量

表7组统计量中给出了三类股票中净利润同比增长率、营业总收入同比增长率、净资产收益率-摊薄及销售毛利率这四项财务指标的均值和标准差。第一类股票的净资产收益率-摊薄和销售毛利率的平均值最高;第二类股票的净利润同比增长率和营业总收入同比增长率的平均值最高;第三类股票的四项财务指标均值都是最低的。
可分析得出第一类营业总收入同比增长率略低于行业平均,其余各项财务指标都高于行业平均,较其他类别而言,第一类盈利能力更强,成长能力也是行业中较强者,对于一个企业而言,成长只是表象,支撑其长期持续成长的则是其盈利能力;盈利能力低下的企业不可能实现长期、持续的高成长,即使通过股权融资短期内实现较高增长,也会因为其资金使用效率低下,仍然是价值毁灭者,所以第一类股票是生物板块中盈利能力特别突出者,适合投资者长期关注、长线投资。
第二类的净利润同比增长率和营业总收入同比增长率超强,远高于行业平均水平,即成长能力超强;成长能力超强则表示此类个股股性活跃,弹性极强,因此在上涨过程中更易激发市场人气。此外,由于此类个股具有较强的续涨能力,往往能够持续拉出阳K线,从而吸引各路资金蜂拥而来,进而聚集市场做多能量,第二类股票适合投资者短期投资。
除了同行业中超强的成长能力,第二类股票的盈利能力也没有落后。第二类股票净资产收益率-摊薄和销售毛利率接近于行业平均,盈利能力也不弱。其中,盈利能力是指企业获取利润的能力,也称为企业的资金或资本增值能力,通常表现为一定时期内企业收益数额的多少及其水平的高低。
第三类四项财务指标都低于行业平均。

表8 汇聚的组内矩阵a
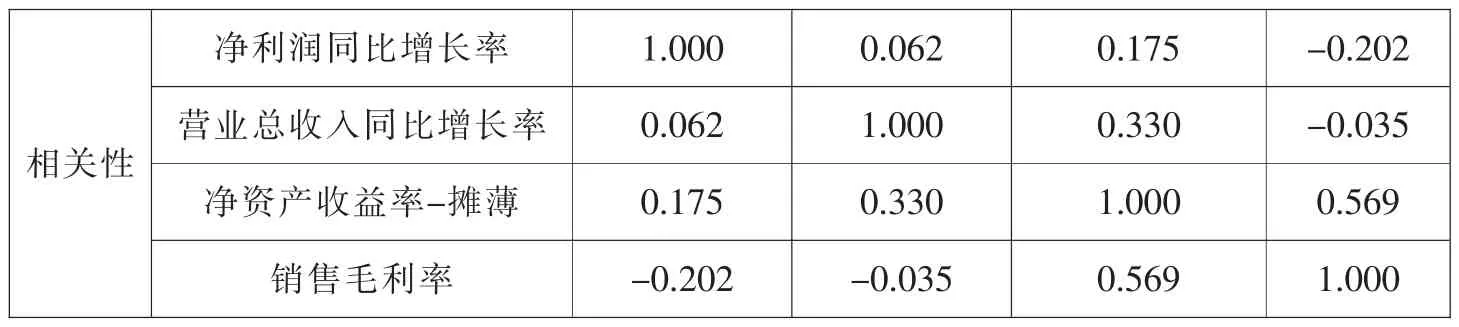
a.协方差矩阵的自由度为29。
表8汇聚的组内矩阵中第一行是合并组内的协方差阵,是依据表7中前三个矩阵计算SSCP后求和并除以自由度得到的结果,第二行是相关系数矩阵。净利润同比增长率和营业总收入同比增长率更相关,共同衡量股票的成长能力,净资产收益率-摊薄和销售毛利率更相关,共同衡量股票的盈利能力。

图1 三次聚类结果及对应的判对率

表9 检验结果
表9检验结果中给出了M、B统计量的观测值,以及对应的概率p值,为0.00.如果显著性水平α为0.05,由于概率p值小于显著性水平α,则应拒绝原假设,认为各类别总体下的判别变量协差阵存在显著差异。
综合以上案例分析结果,从图1可总结聚类结果从90.6%到100%的判对率中完成了最佳的分类,接下来从分类结果中进行各类别的特征性质分析,可以给我们的股票投资提供重要参考意见。
五、结 论
在最佳分类基础上分别对每一类分组进行因子分析,目的是探求每组类别在盈利能力及成长能力方面的特征表现,结合三类的输出结果整理如表10所示。

表10 判对率100%的最佳聚类列表
综上,我们经过聚类分析及贝叶斯判别,最后通过因子分析得出结论,生物板块中的32只股票中,盈利能力及成长能力特别突出的分别是本文中的第一类、第二类股票。
如表10所示,第一类股票适合投资者长期关注与投资。因为盈利能力是决定股票内在价值的核心因素,对于一个企业而言,支撑其长期持续成长的是其盈利能力;盈利能力低下的企业不可能实现长期、持续的高成长。
第二类股票(溢多利、博雅生物、迈克生物、钱江生化)适合投资者进行短期投资。此类个股具有较强的续涨能力,往往能够持续拉出阳K线,从而吸引各路资金蜂拥而来,进而聚集市场做多能量,因此第二类股票适合投资者短期投资。
[1] 薛薇.《统计分析方法及应用》(第三版)[M].北京:电子工业出版社,2013.1.
[2] 邓海燕.聚类分析和判别分析的区别[J].武汉学刊,2006(1),29-31.
[3] 周洪力,董景荣:上市公司投资价值的 FISHER 判别分析[J].统计与决策,2006(14):44-46.
[4] 任志娟.SPSS 中判别分析方法的正确使用[J].统计与决策,2006(2):42-45.
[5] 何晓群.《多元统计分析》(第一版)[M].北京:中国人民大学出版社,2004.
[6] 冬梅.建立我国上市公司业绩综合评价指标体系[J].证券与投资,2001(1):84-87.
[7]杜金岷.论现代证券投资组合理论的发展与局限[J]投资与证券,1999(9):157.
[8]郭志刚.社会统计分析方法——SPSS软件应用[M].北京:中国人民大学出版社,1999.
[9]王力弘.浅议量化投资发展趋势及其对中国的启示[J].中国投资,2013(S2):202-202.
