一种改进的线性分组码的全盲识别算法
2017-03-18王兰勋贾层娟郭淑婷
王兰勋,贾层娟,郭淑婷
(河北大学 电子信息工程学院,河北 保定 071002)
一种改进的线性分组码的全盲识别算法
王兰勋,贾层娟,郭淑婷
(河北大学 电子信息工程学院,河北 保定 071002)
针对线性分组码编码参数的盲识别问题,根据实际与随机序列码重概率分布间较大的差异性,提出了利用两种特征参数(码重标准差率差值、码重信息熵)分别同时识别码长和起始点的算法。根据这两种算法的不足又进一步改进,提出一种对这两种特征参数进行融合来同时识别码长和起始点的算法。在此基础上,通过建立矩阵进行化简获得生成矩阵,从而实现线性分组码的全盲识别。理论分析及实验仿真表明该方法简单易行,容错性较强,在误码率为0.025条件下对中短码识别率达到90%,误码率为0.005条件下对中长码识别率高于80%。
线性分组码;全盲识别;码重标准差率差值;特征参数融合
信道编码盲识别技术可以在所接收编码信息不全的条件下对线性分组码进行盲识别。在通信领域中,信道编码盲识别应用范围较广,它可以在卫星通信、非协作通信等领域对信息进行盲识别,因此具有重要的研究意义[1-3]。
本文针对线性分组码盲识别问题展开研究,但据已有公开发表的文献可知,目前针对线性分组码的全盲识别的研究相对较少。文献[4]利用比特频率检测法估计码长和码字同步点,只适用于较低误码环境,且容错性一般。文献[5]基于码重相似度算法识别码长和码字起始点,只适用于一种先验条件已知的情况,且容错性也一般。文献[6]利用矩阵秩信息熵及码重信息熵分别识别码长和码字起始点,但需要多次构造矩阵,比较复杂。文献[7]利用码重信息熵识别码长,虽适用于较高误码环境,但需已知同步点。文献[8]根据矩阵变换和码重分布来识别码长和起始点,但容错性一般。文献[9]利用码重分布概率方差识别码长,虽然运算量较小,但需要已知同步点。文献[10]利用码重分布距离识别码长和码字起始点,只适用于较低误码的环境。文献[11]根据解调输出的软判决序列求解有错的方程,但运算量所需较大。文献[12]利用“3倍标准差”准则和判断对偶空间归一化维数的最大值来识别码长和码字起始点,但计算量较大。
基于以上分析,上述识别方法中有些容错性一般或者只适用于较低误码环境,有些是必须在码字起始点(码字同步点)已知的条件下才能完成识别,而不能实现全盲识别。为此,本文提出利用码重标准差率差值与码重信息熵进行融合来同时识别码长和起始点的算法,该算法可以实现线性分组码的全盲识别。
1 线性分组码识别基础
定义1[13]:一个(n,k)分组码的基本单位是码字,每个码字是由k个信息位和n-k个监督位组成,如果它的信息位和监督位之间是一种线性的代数关系,则称为线性分组码。

定义3[15]:q元[n,k]线性分组码是GF(q)上的n维线性空间Vn中的一个k维子空间Vn,k,设C是一个q元[n,k]线性分组码,将C的一组基底作为行向量构成一个k×n阶矩阵G,那么G就是线性码C的生成矩阵。将具有[IkP]形式的G矩阵称为典型阵。
定理[13](n,k)线性分组码的k位信息生成的n位码字集v是n维向量空间V的子集,且v在V中的分布一定是非等概的。
2 两种特征参数识别方法
2.1 两种算法描述
对于(n,k)线性分组码而言,码组内各码元之间具有较强的完整的线性约束关系,且不同码重的码组分布是非等概的,而随机序列随机性比较大,所以不具有较强的线性约束关系,导致码重分布不平衡。根据实际序列和随机序列码重分布概率之间的差异最大这一特性,利用码重标准差率差值、码重信息熵两种特征参数来分别对线性分组码进行全盲识别。
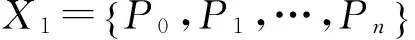
1)码重标准差率差值
定义:实际序列的码重分布概率的CV与随机序列的码重分布概率的CV的差值定义为码重标准差率差值,即
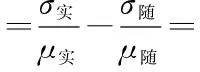

(1)
其中:σ实,σ随表示X1,X2的标准差;μ实,μ随表示X1,X2的均值;CV表示概率分布的离散程度。对于真实序列,码重分布相对集中,即CV较大;对于随机序列,码重分布相对分散,即CV较小。故当遍历到真实的码长和起始点时,真实序列的码重分布概率相对于随机序列较集中,且与随机序列的分布特性相差较大,ΔCV最大。因此当标准差率差值ΔCV最大时,识别出真实的码长和起始点。
2)码重信息熵
定义信息熵函数为
(2)
上述已介绍物理量pi(pi≠0)。经上述分析知线性分组码的码重分布不平衡,其码重分布概率与随机序列的码重分布概率之间的差异性很大,当遍历到真实的码长和起始点时,实际序列具有较强的非随机性,导致码重分布不平衡,与随机序列相差较大,因此当Hn最小时,识别出真实的码长和起始点。
2.2 识别方法的步骤
假设接收序列长度为R,则识别码长、起始点的步骤概括如下:
1)初始化待识别参数:码长为n,n取值范围是3~l,l是指最大可能码长;起始点为m,m取值范围是1~n+1。
2)将截获的实际序列以起始点m开始,按码长n划分为Ω个码字,在每种(n,m)下假设待测矩阵为XΩ×n(n,m)=(x1+(Ω-c)n,x2+(Ω-c)n,…,xn+(Ω-c)n),其中:c=Ω,Ω-1,…,1。

4)求出每种假设(n,m)下的实际序列与随机序列的码重分布概率,利用式(1)、式(2)分别求ΔCV、Hn的值,找出ΔCV最大和Hn最小时对应的(n,m)即为真实的码长和起始点。
2.3 仿真验证及分析
选取(15,5)线性分组码为研究对象,参数设置如下:码组个数为1 000组,误码率为Pe=0.02,起始点设为6。根据2.2节识别步骤,基于ΔCV、Hn两种特征参数的算法的识别仿真结果如图1和图2所示。
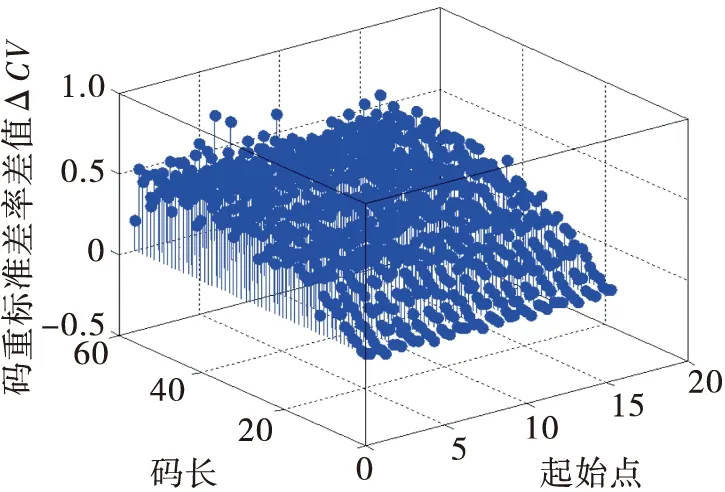
图1 基于ΔCV全盲识别仿真图

图2 基于Hn全盲识别仿真图
从图2中不易清晰地观察出4×4的最小值,所以对式(2)进行改进,对I2取负值,使得码重信息熵最大时识别出真实的码长和起始点。由图2可知0 (3) 根据2.2节识别步骤,基于Sn的仿真结果如图3所示。 图3 基于Sn全盲识别仿真图 经分析可知,码重标准差率差值ΔCV与码重信息熵Sn是衡量对象之间的差异程度,取值最大时,则实际序列和随机序列的差异性较大,此时最大值即为真实的码长和起始点。由图1、图3可知,由于ΔCV与Sn的各个值之间相差范围较小,变化不明显并且不易区分,所以不易实现全盲识别。因此,对这两种特征参数进行融合使变化范围较明显,从而实现全盲识别。 3.1 融合算法描述 通过上一章节对两种特征参数的仿真验证,由图1、图3可知,最大值都不能在仿真图中明显看出,并且它们的值的分布都形似坡状。图1较小值分布在码长为(20,40)的范围内,较大值分布在(40,60)的范围内。而图3较小值分布在码长为(40,60)的范围内,较大值分布在(20,40)的范围内。由于它们较小值与较大值分布范围正好相反,为此本文利用两种特征参数进行相乘,即ΔCV×Sn,使得较小值与较大值相乘后较大值取值变小,而最大值与最大值相乘后使得最大值更加突显,以致于差异明显增大,且仿真图中可以明显看出最大值的位置,从而实现全盲识别。由此,两种特征参数融合的公式为 D=ΔCV×Sn (4) 将式(1)和式(3)代入式(4)可得 (5) 融合特征参数即融合了概率分布的码重标准差率差值和码重信息熵,根据上述对两种特征参数的理论分析,知当D最大时识别出真实的码长和起始点。 3.2 识别方法的步骤 同上章2.2节的识别步骤,将步骤(4)中的公式换成式(5)。 3.3 仿真验证及分析 本次实验选取误码率为Pe=0.02的(15,5),Pe=0.01的(31,11)线性分组码,起始点设为6,及Pe=0.003的(63,18)线性分组码,起始点均设为14,码组个数均为1 000组,利用MATLAB进行仿真实验,识别结果如图4所示。 图4 全盲识别仿真曲线图 由图4三维图可看出,坐标位置分别在(15,6),(31,6),(63,14)处函数值D取得最大值,可知该处的坐标值即为码长和码字起始点的真实值。对于上述3种线性分组码,虽误码率不同,但都能较明显地识别出码长和起始点。经分析知,当码长和起始点为真实值时,码组内具有完整的线性约束关系,实际序列的码重分布概率是非等概的,导致码重分布不平衡,与随机序列的码重分布概率差异性最大,使得融合特征参数D值变化最大,所以D值最大时所对应的为真实的码长和起始点。经仿真验证该算法在一定的误码率条件下可以实现对码长和起始点的全盲识别,且识别效果明显。 4.1 理论描述及分析 (6) 式中:Gk×n即为线性分组码的生成矩阵。 为达到无错误码字最大化进行多次化简计算,选取出现概率最大的一组最大线性无关向量组排列成矩阵进行化简,即完成生成矩阵的识别。 4.2 仿真验证及分析 (7) 对于不同参数的线性分组码,选取(7,4),(15,5),(15,7),(31,11),(63,18)5种线性分组码为研究对象来讨论该融合识别方法的容错性能。在不同误码率下对不同码长均取1 000组码字,进行500次蒙特卡洛仿真实验,运用融合特征参数统计不同误码率下的正确识别率,识别率曲线图如图5所示。 图5 全盲识别概率曲线图 由图5可看出,(7,4)在高误码率为0.17时,识别率达到90%;(15,5)在高误码率为0.21时,识别率达到90%;(15,7)在误码率为0.035时,识别率达到90%;(31,11)在误码率为0.025时,识别率达到90%;(63,18)在误码率为0.005时,识别率高达80%以上。由图可知,对于(15,5)与(15,7)两种码字,随着误码率的增加,前者识别率高于后者,可以看出码长相同、码率不同时,低码率码字识别效果较好。因此从上述分析可以得出,随着误码率、码长和码率的逐渐增大,码组内码字之间的线性约束关系逐渐减弱,使得识别率降低,可见,该识别算法在误码率为0.005条件下,可以有效地实现中长码的全盲识别。 以(15,5)线性分组码作为研究对象,在码字种类和码组个数相同的条件下,对文献[5-6,8-9]和本文算法分别进行500次蒙特卡洛仿真实验。图6为本文算法与文献[6,8-9]码长识别率进行比较,可以看出本文算法在高误码率为0.21时的码长识别概率高达90%,而其他3种算法均没有本文算法容错性好。图7为本文算法与文献[5-6,8]码字起始点识别率进行比较,可以看出本文算法在高误码率为0.21时的码字起始点识别概率达到90%,均优于其他3种算法。因此本文提出的对码重标准差率差值和码重信息熵进行融合来识别码长和同步点的算法比以往算法更具有误码适应能力。 图6 码长识别率比较 图7 同步点识别率比较 本文根据实际与随机序列码重概率分布之间的差异性特征,提出了基于码重标准差率差值、码重信息熵2种特征参数的算法分别同时识别码长和起始点。但通过对2种特征参数的仿真验证分析,发现这2种算法难以实现线性分组码的全盲识别,进而提出了一种将码重标准差率差值与码重信息熵进行融合的全盲识别算法,可同时实现码长与码字同步点的识别。利用线性分组码的特性,建立矩阵进行模二运算化简识别生成矩阵,实现了线性分组码的全盲识别。最后,进行仿真实验,讨论并分析其容错性。结果表明,该算法简单易懂,容错性强于其他文献,在高误码率为0.025情况下能有效地识别中短码,在误码率为0.005情况下能有效地识别中长码。 [1] 闫郁翰.信道编码盲识别技术研究[D].西安:西安电子科技大学,2012. [2] 王兰勋,熊政达,孙旭丽.本原BCH码参数的盲识别方法[J].电视技术,2015,39(17):38-42. [3] 宋镜业.信道编码识别技术研究[D].西安:西安电子科技大学,2009. [4] 陈金杰,杨俊安.一种对线性分组码编码参数的盲识别方法[J].电路与系统学报,2013,18(2):248-254. [5] 王兰勋,佟婧丽,孟祥雅.一种线性分组码参数的盲识别方法[J].电视技术,2014,38(9):188-192. [6] 陈金杰,计同钟,杨俊安.高误码条件下线性分组码的盲识别[J].应用科学学报,2013,31(5):459-467. [7] 陈金杰,杨俊安.基于码重信息熵低码率线性分组码的盲识别[J].电路与系统学报,2012,17(1):41-46. [8] 朱联祥,李荔.改进的二进制循环码盲识别方法[J].计算机应用,2013,33(10):2762-2764. [9] 郑瑞瑞,汪立新.基于码重分布概率方差的循环码识别方法[J].太赫兹科学与电子信息学报,2013,11(5):792-796. [10] 王磊,胡以华,王勇,等.基于码重分布的系统循环码识别方法[J].计算机工程与应用,2012,48(7):150-153. [11] 于沛东,李静,彭华.一种利用软判决的信道编码识别新算法[J].电子学报,2013,41(2):301-306. [12] 杨晓炜,甘露.基于Walsh-Hadamard变换的线性分组码参数盲估计算法[J].电子与信息学报,2012,34(7):1642-1646. [13] 张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010. [14] 赵晓群.现代编码理论[M].武汉:华中科技大学出版社,2008. [15] 陈鲁生,沈世镒.编码理论基础[M].北京:高等教育出版社,2005. 王兰勋(1956— ),教授,主要从事数字通信与信息编码方面研究; 贾层娟(1988— ),女,硕士生,主研信道编码盲识别; 郭淑婷(1992— ),女,硕士生,主研调制识别。 责任编辑:闫雯雯 Improved blind recognition method of linear block code parameters WANG Lanxun, JIA Cengjuan, GUO Shuting (CollegeofElectronicandInformationalEngineering,HebeiUniversity,HebeiBaoding071002,China) In view of the problem of the blind recognition of linear block code parameters, the code length and synchronization point are simultaneous identified by the recognition method based on the two characteristic parameter(standard error rate difference of code weight and information entropy of code weight)that is proposed by the difference of code weight distribution probability between the actual sequence and random sequence. According to the deficiency of these two algorithms, then a new method of fusion of two characteristic parameters is put forward that code length and synchronization point can be simultaneous identified. And through establishing matrix and simplifying Matrix, and identify the generator matrix to achieve a blind identification linear block codes.Theoretical analysis and simulation experience show that the recognition method is simple and has better error-tolerance, and the recognition method 90% with middle and short code length can be recognized when BER is 0.025 and has better performance more than 80% about slightly long code in 0.005BER. linear block code;blind recognition;standard error rate difference of code weight;characteristic parameter fusion 王兰勋,贾层娟,郭淑婷.一种改进的线性分组码的全盲识别算法[J].电视技术,2017,41(2):77-82. WANG L X, JIA C J, GUO S T. Improved blind recognition method of linear block code parameters [J]. Video engineering,2017,41(2):77-82. TP391 A 10.16280/j.videoe.2017.02.016 河北省自然科学基金项目(F2014201168) 2016-04-28
3 融合两种特征参数识别方法

4 生成矩阵的识别
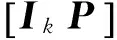

5 比较分析容错性



6 结论
