基于FrFT的差分跳频通信LFM干扰抑制算法*

李喆，李潇，钱博

（1.中国运载火箭技术研究院，北京100076；2.沈阳理工大学，沈阳110159）

基于FrFT的差分跳频通信LFM干扰抑制算法*

李喆1，李潇1，钱博2

（1.中国运载火箭技术研究院，北京100076；2.沈阳理工大学，沈阳110159）

针对差分跳频通信系统抗LFM干扰能力不足的问题，利用差分跳频信号和LFM干扰信号调频斜率参数的不同，通过估计采样信号中LFM干扰信号的调频斜率K和旋转阶次α参数，结合分段、参数估计和均值处理提高估计精度，进一步在采样信号的分数阶时频域二维参数平面（α，μ）中利用LFM干扰信号频带外的平面均值替代LFM信号成分，实现对差分跳频通信中LFM干扰信号的抑制。仿真结果表明，该算法可有效抑制差分跳频信号中LFM干扰信号，提高信噪比约11 dB。

差分跳频，FrFT，干扰抑制，LFM

0 引言

跳频（Frequency Hopping，FH）通信系统的信号频率随时间变化，不易被截获，具有较强的抗干扰性，被广泛应用于保密通信领域［1］。在各类跳频通信系统中，差分跳频（Differential Frequency Hopping，DFH）通信系统利用相邻跳信号频率变化传输数据，跳速更高、抗干扰性更强，可有效抵抗窄带干扰和跟踪干扰［2］。

线性调频（Linear Frequency Modulation，LFM）信号［3］具有宽带非平稳特性，对差分跳频通信系统的影响较大。

国内外针对LFM信号干扰抑制方法主要有基于短时傅里叶变换（Short-time Fourier Transform，STFT）［4］、WVD（Wigner-Ville Distribution）变换［5］、小波变换［6］和分数阶傅里叶变换［7-8］（FractionalFourier Transform，FrFT）等方法，其核心机理是先通过估计LFM干扰信号参数后进行消除。但STFT变换的能量积聚性较差，且分辨率较低；Wigner变换对LFM信号具有良好能量积聚性，但算法复杂、计算量较大；小波变换适合抑制具有突发特征的脉冲式干扰，同样算法复杂、计算量大；FrFT变换将信号能量在旋转角度α和调频斜率μ构成的二维参数平面上进行分析以识别LFM信号，但设置合理的阈值门限是难点。

为降低LFM干扰信号对差分跳频通信系统的影响，本文提出一种基于FrFT的LFM干扰抑制算法，通过对接收信号进行不同阶次的FrFT变换，提取最优阶次并识别LFM干扰信号，进一步在二维参数平面（α，μ）上进行干扰信号陷波，从而实现LFM干扰抑制。

1 差分跳频通信脆弱性和LFM信号特性分析

1.1 差分跳频通信脆弱性分析

差分跳频通信系统利用相邻跳的频率变化传输数据，信号频率随时间跳变。单跳差分跳频信号表达式如下式：

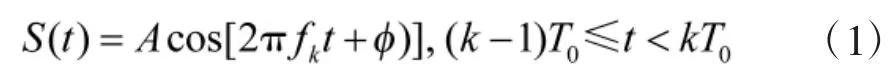
其中，A为信号振幅；fk为当前跳频率；φ为初始相位；T0为每跳驻留时间。

差分跳频信号每跳频率fk由上一跳频率fk-1和当前传输信息数据Xk根据G函数规则产生，可表示为：

其中，G（.）为G函数产生规则。

在差分跳频接收端采用加窗FFT宽带接收，计算跳频带宽内各个跳频频点的能量值，利用软判决维特比译码器，根据相邻时刻连续两跳信号频率fk-1和fk，由G函数的逆变换，恢复出发送的信息符号流Xk，即

其中，G-1（.）表示G函数的逆变换，即要求G函数必须具有可逆性。将得到的信息符号流Xk再通过符号-比特转换器得到传输的信息数据。

由式（1）～式（3）可知，差分跳频通信技术集调制、解调和跳频图案于一体。由于传输信息数据具有随机性，因而差分跳频信号的跳频图案也具有随机性；单跳差分跳频信号载波上不调制数据，使得信号功率集中，带宽较窄，可实现较高跳速；通过增加G函数规则中每跳频点的扇出系数，可有效提高传输数据率。

可见，差分跳频通信系统具有的高跳速和跳频图案随机特性利于其抵抗跟踪干扰和窄带干扰。但由于在接收端需要进行FFT宽带接收，因而抗宽带干扰能力相对较弱。

1.2 LFM信号特性分析

LFM信号可表示为：

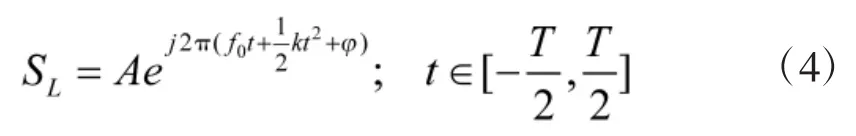
其中，A为信号幅度；f0为初始频率；k为调频斜率；φ为初始相位。

LFM信号的包络为一个矩形函数，时宽为T，带宽B=KT，时宽带宽乘积D=kT2，瞬时频率随时间呈现线性变化关系：

由上式可以看出在时频平面上，线性调频信号表现为一条斜率为k的直线。

LFM信号广泛运用于各种体制的雷达当中。它具有大时宽带宽积，采用这种信号的雷达可以同时获得远的作用距离和距离分辨力。

由于LFM信号带宽较宽，对差分跳频信号有很大的干扰，可能会产生覆盖式干扰，影响通信质量，甚至阻断差分跳频通信过程。

2 基于FrFT的LFM干扰抑制算法

2.1 FrFT变换

分数傅立叶变换FrFT是傅立叶变换的一种广义形式，作为传统傅里叶变换的完善、丰富和发展，在光学、信号处理、图像处理、声纳、雷达及通信等领域得到了广泛应用。

差分跳频信号S（t）的FrFT变换是信号在时间轴逆时针旋转角度α后在分数阶时频域二维参数平面（α，μ）上的投影，可表示为：

式中，FrFT的变换核ka（t，u）可表示为：

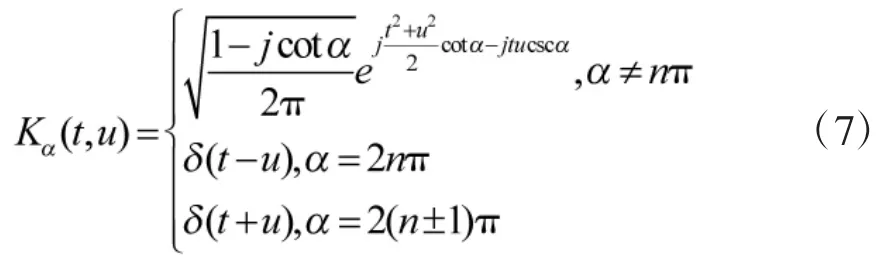
式中，δ（t）为冲击函数，n∈z。

若α=0即是传统没有变换的时域信号，α=π则是S（t）的传统傅立叶变换。在传统傅立叶变换中基函数为正弦函数，在经典分数傅立叶变换中，基函数具有Chirp信号的表现形式。差分跳频信号可视为调频斜率为1的特殊LFM信号［9］。LFM信号的FrFT变换为［10］

若取f0=ucsca，k=-cota，p=2a/π=-2arc cotk/π，则可得到在p阶FrFT变换域中集中LFM能量的脉冲峰值，其表达式如下：

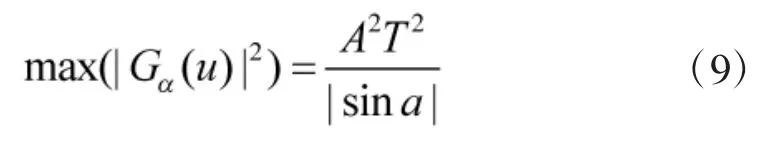
可见，在特定的k和α参数条件下，利用式（9）中的脉冲峰值可以识别出LFM干扰信号，进一步可将其在差分跳频干扰信号中消除，从而实现抑制。但对于通信方而言，无法预知调频斜率k和旋转阶次α，对LFM干扰信号的识别和干扰消除造成了困难。

文献［11］提出了线性调频信号调频斜率K和旋转阶次α的估价方法，其核心步骤为：首先，将采样信号进行延时共轭相乘，并进行FFT处理，得到峰值点频率，从而推出调频斜率K，进而求出粗略的旋转阶次α0；进一步以α0为中心，在±Δα范围内进行谱峰最大值搜索，从而得到精确的α值，进行LFM信号提取。本文对文献［11］算法进行改进，通过将采样信号进行分段、参数估计和均值处理，提高线性调频信号调频斜率K和旋转阶次α的估计精度。

2.2 LFM干扰抑制

通过对差分跳频信号和LFM信号的FrFT变换理论分析可见，差分跳频信号的调频斜率与LFM信号不同，通过估计采样信号中LFM干扰信号的调频斜率K和旋转阶次α参数，进一步从采样信号的分数阶时频域二维参数平面（α，μ）中将LFM干扰信号频带外的平面均值替代LFM信号成分，实现LFM干扰抑制。

基于FrFT的LFM干扰抑制算法处理流程如图1所示。

算法处理步骤如下：

Step1：首先对接收数据进行加窗处理，并进行分段延时共轭相乘；

Step2：对共轭相乘结果进行FFT处理，统计峰值能量；

Step3：加窗数据进行FrFT变换；

Step4：粗估计调频斜率K和旋转阶次α0；

Step5：以α0为中心，在±Δα范围内进行谱峰最大值搜索，并进行均值处理精估计α参数；

Step6：利用估计得到的α参数，检测接收数据中是否存在LFM干扰信号，存在则程序继续，否则跳转到Step10；

Step7：提取分数阶傅里叶变换后LFM干扰信号能量；

Step8：计算分数阶时频域二维参数平面（α，μ）中不包含LFM干扰信号的均值；

Step9：消除接收数据分数阶傅里叶变换后LFM干扰信号成分；

Step10：消除干扰后信号FrFT变换；

Step11：差分跳频接收处理；

Step12：程序结束。

3 仿真分析

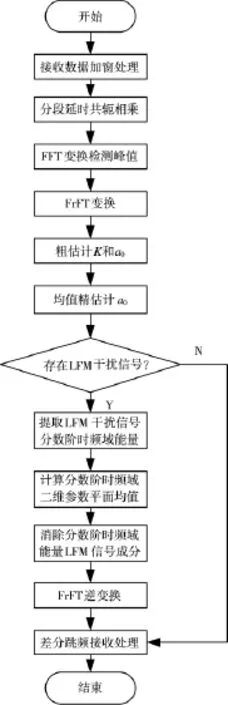
图1 基于FrFT的LFM干扰抑制算法流程

为验证基于FrFT的差分跳频通信LFM干扰抑制算法的有效性，在软件条件下对算法功能和性能进行仿真验证。仿真产生差分跳频信号参数为：信号幅度为1 V，跳频带宽2 MHz～25 MHz，跳频频点数64，采样频率100 MHz，跳速892 Hops/s，跳驻留时间为1.12 ms。LFM信号参数为：信号幅度为V；调频斜率为20 KHz；初始相位为0。在信噪比为5dB，干信比为1 dB～15 dB的条件下，进行算法有效性验证。

图2 接收信号在5 dB下的时域波形

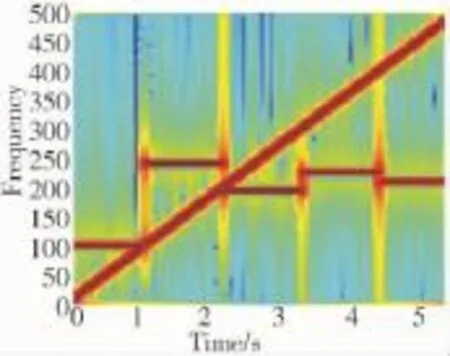
图3 接收信号在5 dB下的时频分析结果

图2和图3分别是混合信号在环境噪声为5 dB高斯白噪条件下的时域波形和时频域分布结果。

从图2和图3可见，DFH通信信号在时域上与LFM干扰信号重叠，频域上LFM干扰信号覆盖差分跳频通信信号带宽。

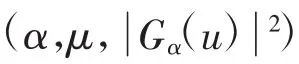
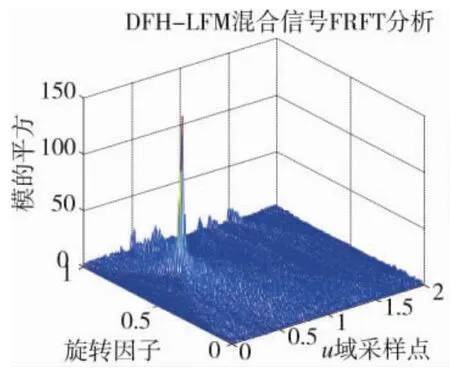
图4 接收信号在5 dB下的FrFT三维投影结果

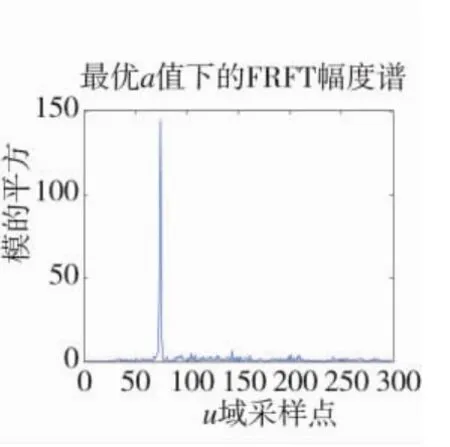
图5 接收信号在最优阶次下的FrFT结果

将图6抑制LFM干扰信号后的分数阶时频域变换结果进行FrFT逆变换，得到结果如图7所示。

从图7可见，抑制LFM干扰信号后的接收信号与原始DFH信号相比存在一定的误差，这是由于在进行LFM抑制时损失了一部分频率的能量值。

图6 抑制LFM干扰后的FrFT结果

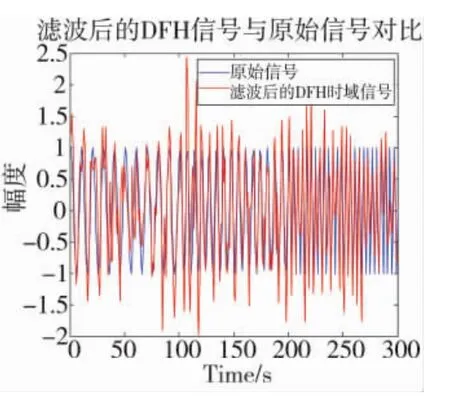
图7 抑制LFM干扰后逆FrFT变换结果

在不同干信比条件下，抑制LFM干扰后信号与DFH通信信号在2 MHz～25 MHz范围内的最小均方误差如图8所示。

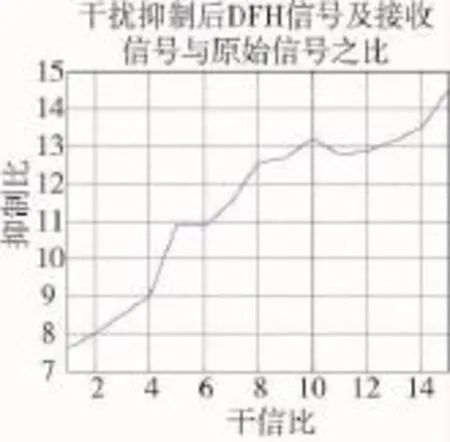
图8 不同干信比对LFM信号的抑制能力

从图8可见，随着干信比的增大，本文算法抑制LFM干扰信号的能力有所增强，这是由于即使LFM信号增大干扰功率，经过FrFT的消除后，对差分跳频信号的干扰也被基本消除。在2 MHz～25 MHz范围内可有效提高LFM干扰信号抑制比约11 dB。

通过仿真分析可见，基于FrFT的差分跳频通信LFM干扰抑制算法可有效消除接收信号中的LFM干扰信号成分，提高接收信噪比。

4 结论

本文针对差分跳频通信抗LFM干扰能力较差的问题，利用差分跳频信号和LFM干扰信号不同参数下FrFT变换特性的不同，通过估计LFM干扰信号旋转阶次，提取LFM干扰信号在分数阶时频域二维参数平面（α，μ）的投影，进一步将其在接收信号的分数阶时频域二维参数平面中消除，实现对差分跳频通信中LFM干扰信号的抑制。利用本文算法可有效提高差分跳频接收处理信噪比，具有一定的实际应用价值。

［1］全厚德，李苏阳.一种跳频抗干扰方案的设计及其性能分析［J］.海军工程大学学报，2013，25（4）：68-73.

［2］滕振宇，冯永新.差分跳频通信抗干扰效能分析［J］.火力与指挥控制，2012，37（1）：11-15.

［3］宋军，刘渝，刘云飞.LFM信号参数估计的插值FrFT修正算法［J］.信号处理，2012，28（1）：112-117.

［4］MILLIOZ F，MARTIN N.Circularity of the STFT and spectral kur-tosis for time-frequency segmentation in Gaussian environment［C］//New Brunswick，IEEE Transactions on Signal Processing，2011，59（2）：515-524.

［5］林炎，张友益.超级WVD对多分量LFM信号参数的估计［J］.现代雷达，2014，36（1）：47-51.

［6］LANDRY R J R，MOUYON P，LEKAIM D.Interference mitigation in spread spectrum systems by wavelet coefficients thresholding［J］.Kyiv，Euro Trans Telecomm，2008，9（2）：191-202.

［7］付霖宇，张鑫，程永茂.基于分数阶傅里叶变换的线性调频连续波信号检测［J］.科学技术与工程，2014，14（5）：93-95.

［8］臧顺全，王竹霞.基于分数傅里叶变换的信号检测方法［J］.科学技术与工程，2010，10（3）：651-655.

［9］程乃平，席有猷，郝建华.基于分数阶傅里叶变换的LFM干扰抑制算法［J］.装备学院学报，2014，25（1）：73-77.

［10］申丽然，郭黎利，尹清波.基于分数阶傅里叶变换的直扩通信快速线性调频干扰抑制［J］.科学技术与工程，2014，14（1）：59-65，71.

［11］郭波，宋李彬，周贵良.分数阶傅里叶滤波在欺骗干扰中的应用研究［J］.电子学报，2012，40（7）：1328-1332.

A Method of LFM Interference Suppression for DFH Communication Based on FrFT

LI Zhe1，LI Xiao1，QIAN Bo2
（1.China Academy of Launch Vehicle Technology，Beijing 100076，China；2.Shenyang Ligong University，Shenyang 110159，China）

Direct to the poor ability of DFH Communication System to anti LFM interference. Using the different slope parameters of FM between the DFH signals and LFM signals，the frequency modulation slope K and the rotating order α of LFM interference signal are estimated.The estimation accuracy is improved by combining with the section and mean treatment.Furthermore，the LFM signal components in the fractional frequency domain dimensional parameter plane（α，μ）are replaced by using the mean plane outside the LFM interference signal frequency band.The LFM interference signal is suppressed in DFH communication.The simulation results show that the algorithm can effectively mitigate LFM interference in DFH communication to improve the SNR about 11 dB.

differential frequency hopping，FrFT，Interference mitigation，linear frequency modulation

TP914.4

A

1002-0640（2017）02-0025-04

2016-01-05

2016-02-17

国家自然科学基金（61301256）；辽宁省教育厅科学研究基金（L2015462）；沈阳理工大学辽宁省信息网络与信息对抗技术重点实验室开放基金资助项目

李喆（1986-），男，山东菏泽人，硕士，工程师。研究方向：信息网络技术、信息对抗技术。