一类非线性系统的自适应模糊反推近似滑模控制*

汪涛，胡剑波，李飞，郑磊

（空军工程大学装备管理与安全工程学院，西安710038）

一类非线性系统的自适应模糊反推近似滑模控制*

汪涛，胡剑波，李飞，郑磊

（空军工程大学装备管理与安全工程学院，西安710038）

针对一类含有未知非线性函数项和外界干扰的不确定纯反馈非线性系统，提出了一种自适应模糊反推近似滑模变结构控制方法。采用中值定理和隐函数定理使未知非仿射输入函数拥有显式的控制输入，利用模糊系统逼近未知非线性函数，动态面控制技术解决了反推设计中出现的“微分爆炸”问题。所提出的自适应近似滑模控制方案削弱了传统滑模控制中的抖振现象。从理论上证明了所设计的控制器能够保证闭环系统所有信号半全局一致终结有界。仿真算例验证了算法的有效性。

纯反馈非线性系统，动态面控制，反推设计，模糊系统，近似滑模

0 引言

自20世纪70年代以来，非线性系统控制理论取得了大量的研究成果。然而，大多数研究成果都是严反馈非线性系统领域［1-3］的，由于非仿射系统的控制作用包含在非仿射函数中，这种非仿射特性使得控制器的设计变得十分困难［4］，因而取得的成果相对较少。实际工程实践当中，很多系统都具有非仿射特性［5-7］。因此，纯反馈非线性系统控制受到了越来越多的关注。

针对具有非仿射特性的这类非线性系统，常用的控制方法是利用近似线性化、泰勒级数、逆系统等方法。但这些方法往往只能保证控制系统的局部稳定，无法实现系统的大范围控制。针对这一问题，很多学者做了大量的研究，见文献［8-14］。

受前面文献的启发，本文针对一类含有未知非线性函数项和外界干扰的不确定纯反馈非线性系统，利用隐函数定理与中值定理将非仿射型系统转换为仿射型系统，利用模糊系统的万能逼近能力逼近系统未知非线性部分并取消不确定干扰上界先验已知的条件，采用自适应反推设计策略设计控制器，采用动态面技术解决反推设计过程中出现的“微分爆炸”问题，近似函数的引入使得控制信号更为平滑、连续。稳定性分析表明，本文所提出的控制方案在保证闭环系统所有信号有界的同时，可以通过参数选取实现对参考指令信号任意精度的跟踪。

1 问题描述及准备

考虑如下一类不确定纯反馈非线性系统

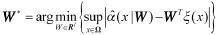
控制目标：在满足假设1～3的条件时，设计自适应模糊反推近似滑模控制器使得不确定纯反馈非线性系统（1）存在未知非线性函数和不确定外界干扰时，闭环系统所有信号半全局一致终结有界，且输出y能够稳定跟踪参考指令信号yr。

2 控制器设计

采用反推控制方法，控制器设计分为n步，控制器设计可以分为两个阶段：第1阶段（Step1～Step n-1）：利用模糊系统的万能逼近能力，结合动态面控制和反推设计方法，处理未知非线性函数项；第2阶段（Step n）：结合滑模控制方法，使系统对于匹配不确定性具有鲁棒性，采用近似函数代替开关函数有效地消除控制抖振。具体设计步骤如下：

Step1：定义系统的跟踪误差，即第1阶子系统误差为e1=x1-yr。e1的导数为

Stepi（2≤i≤n-1）：定义系统的第i（i=2，…，n-1）阶子系统误差为ei=xi-βi-1。ei的导数为

βi-1为第i-1阶子系统虚拟控制αi-1通过一阶滤波器后的输出，则有

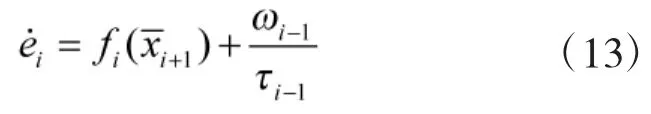
根据隐函数定理与中值定理可得

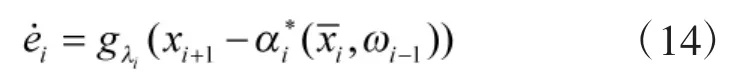
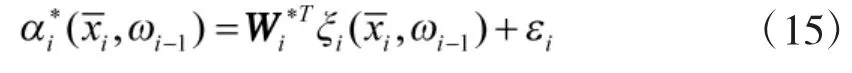
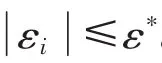
选取第i阶子系统的虚拟控制律

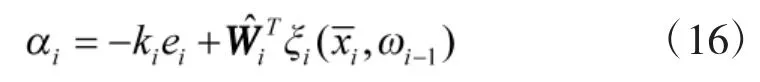
其中，ki＞0为待设计参数。i为最优权值向量的自适应估计值。

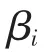
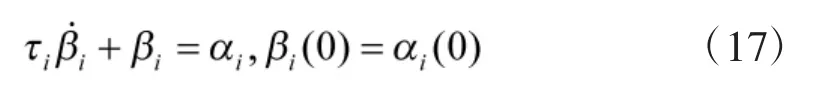
其中，i为滤波器时间常数。

Stepn：定义系统的第n阶子系统误差为en=xnβn-1。en的导数为

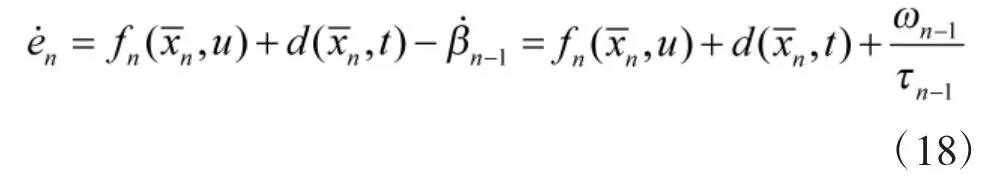
由中值定理知

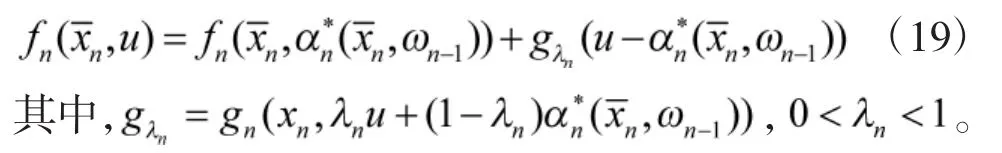
将式（19）代入式（18），可得

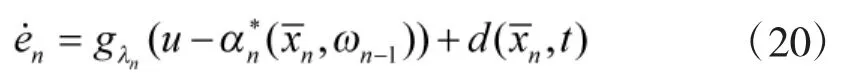
由于铁路货车轴承为双列圆锥滚子轴承，而双列圆锥滚子轴承结构复杂、故障特征频率难以精确计算，且早期微弱故障往往又淹没于系统噪声而难于提取，加之各种频率成分交加使得频率成分更加复杂，因此采用传统方法进行故障精密诊断十分困难，直接对其进行频谱分析往往不能成功，所以可借助共振解调技术对采集的振动信号进行分析与处理。

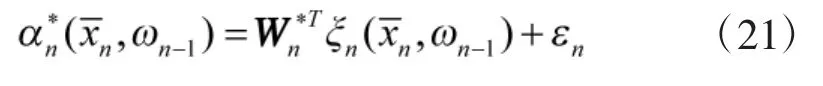
为了增强系统鲁棒性，补偿系统不确定外界干扰对系统跟踪控制效果的影响，采用滑模变结构控制方法设计第n阶子系统控制律。选取滑模面s=en，则可以设计系统最终控制律为

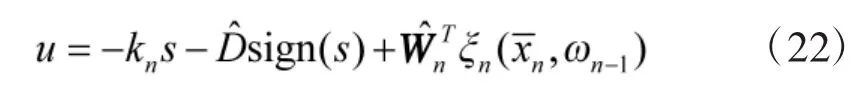
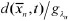
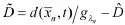
为抑制控制输入存在的抖振现象，采用如下连续可导函数近似控制律中的符号函数：

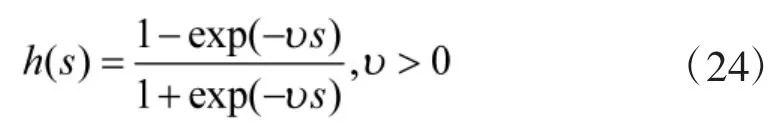
可以得到连续且可导的近似滑模变结构控制律

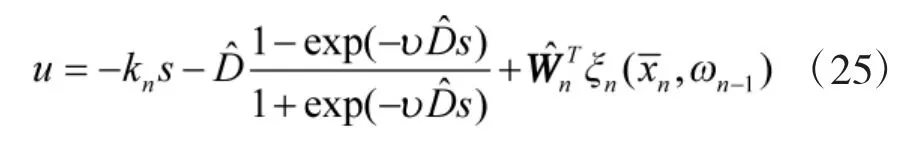
3 稳定性分析

证明：对于闭环系统（1），选取Lyapunov函数

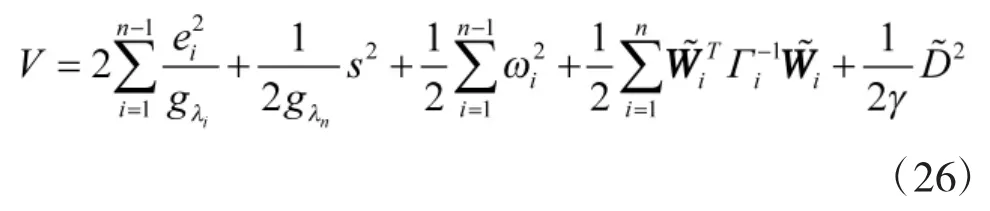
对V求导，可得

第i+1阶子系统误差为

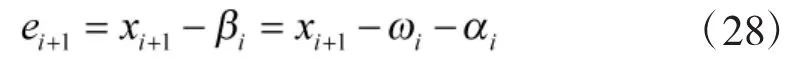
由式（7）、式（8）和式（28），可得

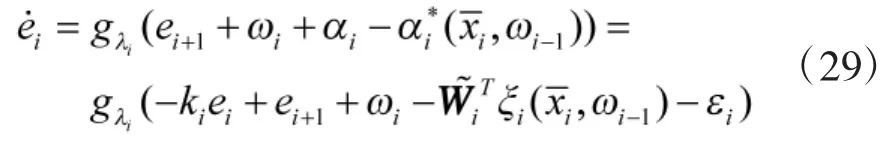
对s求导，可得

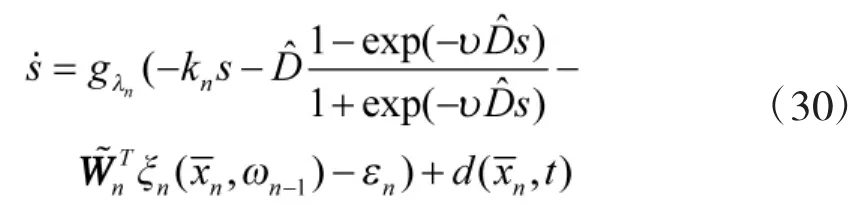
将式（30）代入式（28）对ωi求导，可得

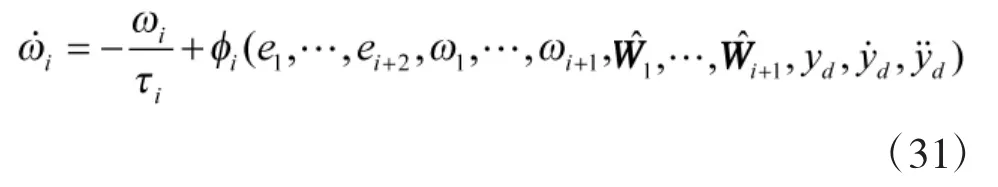
由界化不等式和假设3，可知

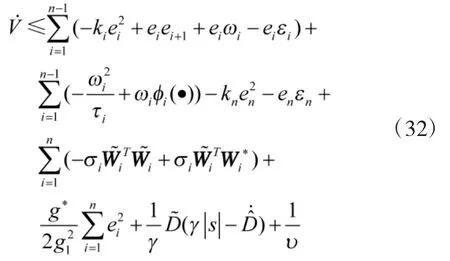
将自适应律（23）代入式（32）可得

根据Young不等式可得

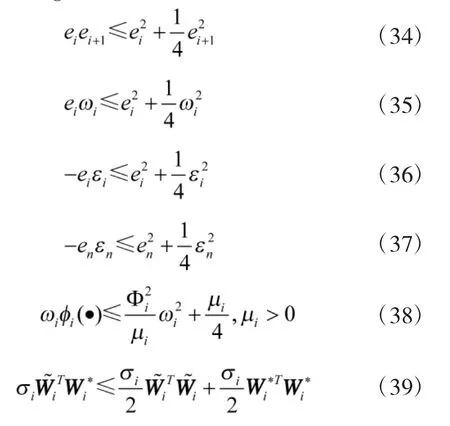
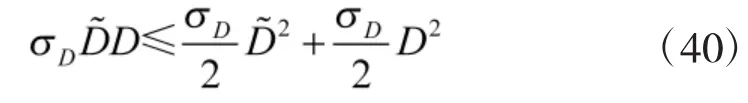
将式（34）～式（40）代入式（33），可得

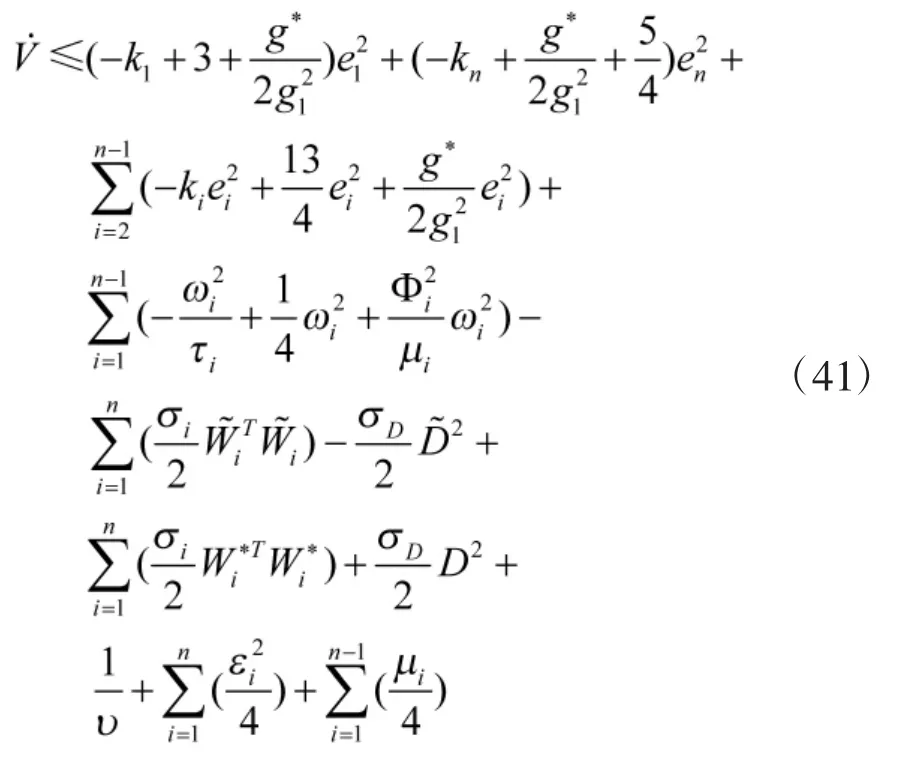
若设计参数满足

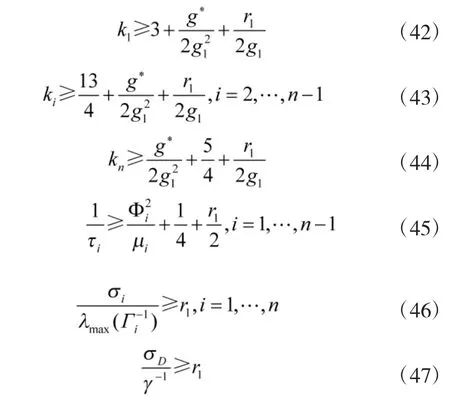
其中，r1＞0。则有

其中，r2为有界常数。

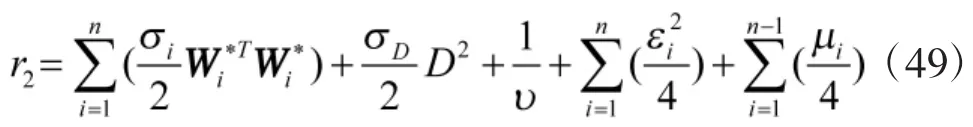
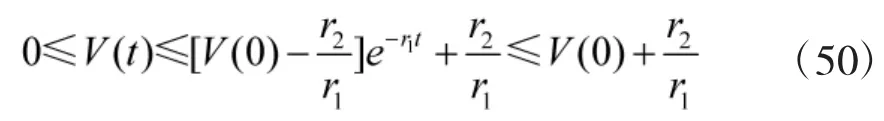
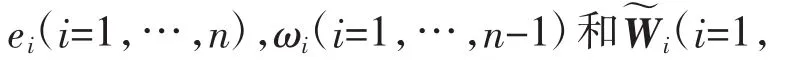
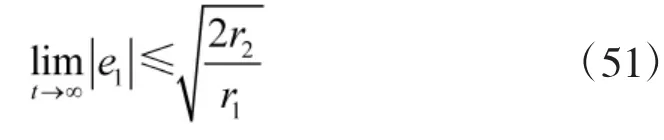
证毕。

4 仿真实例

考虑如下三阶非仿射纯反馈非线性系统：

仿真结果如图1～图6所示。图1为系统输出y跟踪参考指令信号yr轨迹变化曲线，可以看出，在自适应反推近似滑模控制律作用下，系统输出能够实现对参考指令信号的稳定跟踪，并且跟踪误差能够控制在较小范围内。图2～图4分别为模糊系统对系统中未知非线性函数α1、α2、α3的逼近效果，逼近效果可以通过模糊器参数进行调整，图5为基于lyapunov稳定性理论设计的自适应参数Dˆ的变化曲线，可以看出，闭环系统所有状态有界。

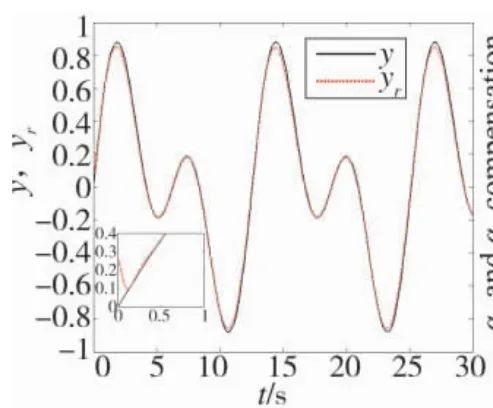
图1 系统输出跟踪参考指令信号轨迹

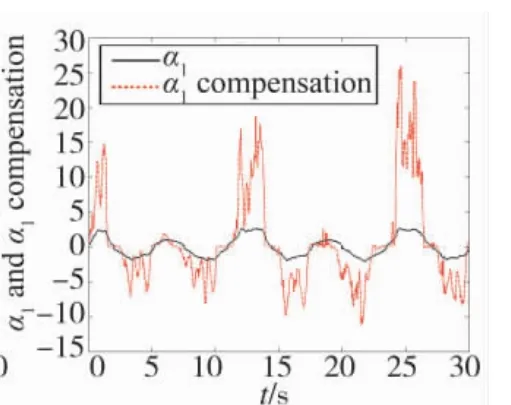
图2 函数α1模糊逼近效果

图6为采用近似变结构控制策略下的控制输入信号曲线，若采用传统不连续的滑模变结构控制方案（22）。其控制输入信号曲线如图7所示。对比分析可知，近似滑模变结构控制方法能够有效削弱传统滑模不连续控制器所产生的抖振现象。

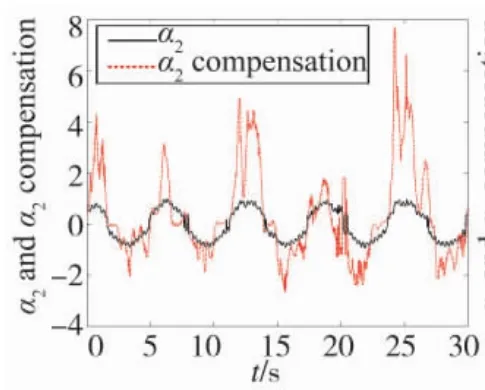
图3 函数α2模糊逼近效果

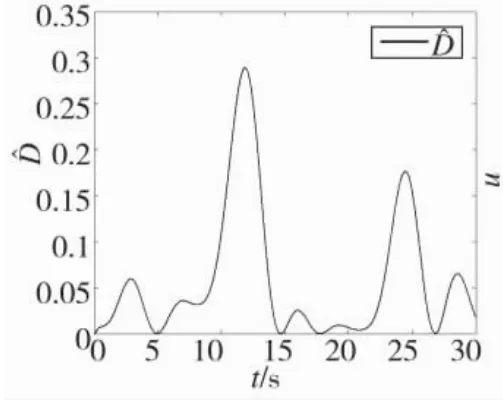
图5 自适应参数

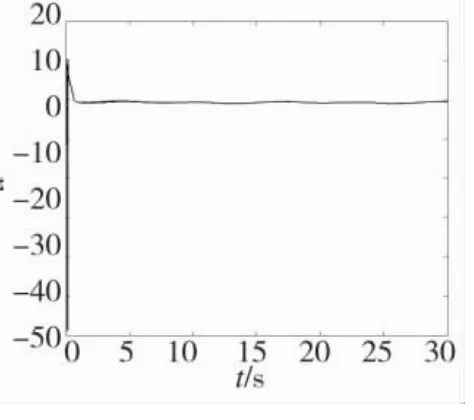
图4 函数α3模糊逼近效果

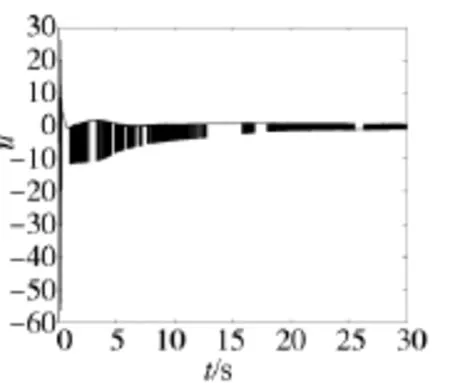
图7 控制输入信号（不连续控制器）

5 结论

本文研究了一类n阶不确定非仿射纯反馈非线性系统自适应反推滑模控制问题，利用中值定理和隐函数定理将相应子系统转化为类仿射系统。利用模糊系统的万能逼近能力逼近系统未知非线性部分，采用自适应反推设计方案设计控制器，使控制器的设计系统化，动态面控制技术解决了反推控制器计算复杂性的问题和非仿射纯反馈非线性系统中可能存在的控制器循环结构问题。近似滑模控制使得控制信号更为平滑、连续，削弱了传统滑模控制中的抖振现象，取消了不确定干扰上界先验已知的条件。应用Lyapunov稳定性理论对所设计的闭环控制系统稳定性进行了分析，证明了系统所有信号半全局一致终结有界，可以通过参数选取实现对参考指令信号任意精度的跟踪。

［1］CALIFANO C，BATTILOTTI S.Dynamic feedback lineariza-tion of two input nonlinear systems［J］.IFAC Proceedings Volumes，2005，38（1）：447-452.

［2］FIDAN B，GAZI V.Target tracking using adaptive gain backstepping control［J］.IFAC Proceedings Volumes，2010，43（10）：83-88.

［3］QIAO F，ZHU Q，WINFIELD A F T，et al.Adaptive sliding mode control for MIMO nonlinear systems based on fuzzy logic scheme［J］.International Journal of Automation and Computing，2004，1（1）：51-62.

［4］刘树光，孙秀霞，董文瀚，等.一类纯反馈非线性系统的简化自适应神经网络动态面控制［J］.控制与决策，2012，27（2）：266-270.

［5］丁青青，王树民，郭静波.HVDC非仿射非线性系统的定电流定电压控制［J］.清华大学学报（自然科学版），2004，44（10）：1325-1328.

［6］WANG H，CHEN B，LIU X，et al.Robust adaptive fuzzy tracking control for pure-feedback stochastic nonlinear systems with input constraints［J］.IEEE transactions on cybernetics，2013，43（6）：2093-2104.

［7］WANG H，CHEN B，LIN C，et al.Observer-based adaptive neural control for a class of nonlinear pure-feedback systems［J］.Neurocomputing，2016（171）：1517-1523.

［8］李平，金福江.未知仿射非线性系统的执行器容错控制设计［J］.控制工程，2014，21（1），107-110.

［9］胡云安，程春华，邹强，等.非仿射纯反馈系统的间接自适应神经网络控制［J］.控制理论与应用，2014，31（4），467-424.

［10］刘勇华.一类纯反馈非线性系统的反推控制［J］.控制理论与应用，2014，31（6）：261-264.

［11］WANG M，LIU X P，SHI P.Adaptive neural control of pure-feedback nonlinear time-delay systems via dynamic surface technique［J］.IEEE Transactions on Systems，Man and Cybernetics-Part B：Cybernetics，2011，41（6）：1627-1692.

［12］WANG C，HILL D J，GE S S et al.An ISS-modular approach for adaptive neural control of pure-feedback systems［J］.Automatica，2006，42（5）：129-191.

［13］SUN G，WANG D，LI X Q，et al.A DSC approach to adaptive neural network tracking control for pure-feedback nonlinear systems［J］.Applied Mathematics and Computation，2013，219（11）：6224-6235.

［14］ZHANG T P，GE S S.Adaptive dynamic surface control of nonlinear systems with unknown dead in pure feedback form［J］.Automatica，2008，44（7）：1355-1903.

Adaptive Fuzzy Backstepping Approximate Sliding Mode Control for A Class of Nonlinear Systems

WANG Tao，HU Jian-bo，LI Fei，ZHENG Lei
（School of Materiel Management and Safety Engineering，Air Force Engineering University，Xi’an 710038，China）

An adaptive fuzzy backstepping approximate sliding mode variable structure control approach is presented for a class of pure-feedback nonlinear systems with uncertainties and external interference.By using implicit function theorem and mean value theorem，unknown non-affine input functions can be transformed to partially affine forms，the fuzzy system is used to approximate the unknown nonlinearities in systems，the problem of explosion of complexity in traditional backstepping design is eliminated by utilizing dynamic surface control.By using adaptive approximate sliding mode control，the earthquake shaking phenomenon in traditional sliding mode control is decreased.At last，the proposed controller ensures the semi-global uniformly ultimately boundedness for all the closed loop signals.A numerical example is presented to demonstrate the effectiveness of the proposed algorithm.

pure-feedback nonlinear systems，dynamic surface control，backstepping，fuzzy system，approximate sliding mode

TP 273

A

1002-0640（2017）02-0034-05

2016-01-05

2016-02-27

国家重点实验室基金资助项目（ICT1401）

汪涛（1992-），男，四川峨眉人，硕士。研究方向：变结构控制理论与应用、信息系统工程。