考虑动态充电负荷需求与多因素影响的电动汽车充电负荷模型

柯慧敏，邵军军，石进永



考虑动态充电负荷需求与多因素影响的电动汽车充电负荷模型

柯慧敏1,2，邵军军1,2，石进永1,2

(1. 南瑞集团公司，江苏 南京 211116；2. 国电南瑞科技股份有限公司，江苏 南京 211116)

考虑不确定充电负荷需求，分析多种重要影响因素对充电负荷的作用机制。提出一种基于电动汽车动态充电负荷需求，分别考虑峰谷电价、天气条件、出行目的影响的电动汽车充电负荷模型。以南京市电动汽车充电负荷为例，进行蒙特卡洛分析，仿真结果表明：峰谷电价机制下，谷荷有大幅提高，峰荷有所下降且峰荷出现时间向后推延；良好天气条件下的负荷整体水平高于恶劣天气情况，而恶劣天气的充电负荷波动强于良好天气；通勤模式下的整体负荷水平高于非通勤出行，且负荷水平随典型通勤时间波动。

动态充电负荷；峰谷电价；天气；出行目的

0 引言

准确估算电动汽车充电负荷是大规模发展电动汽车与电动汽车充电设施的基础[3]，对电动汽车充电负荷的优化控制也起重要支撑作用。不同于传统电力负荷，电动汽车充电负荷具有极强的波动性，但从电动汽车集群而言，又遵循某种规律性[4]。波动性主要是由用户个体充电的不确定性带来的，电动汽车充电负荷易受峰谷电价、天气条件、出行目的等多种相关随机因素的影响，任何一种因素的变化都会造成负荷的巨大波动。规律性主要表现在规模化电动汽车的充电行为从整体上符合一定变化趋势。因此，必须充分考虑充电负荷的不确定性与规律性才能准确分析电动汽车负荷的变化规律。目前绝大多数研究在分析电动汽车充电负荷特性时，多数都是基于规律性对电动汽车充电行为进行概率模拟[5-10]，极少考虑动态充电负荷需求，在分析电动汽车充电负荷影响因素时，也忽略了外部随机因素对用户用车行为的影响。

本文对用户充电行为的不确定性进行建模，以南京市2020年的电动汽车预测保有量为例，分析多种电动汽车充电负荷随机因素的影响，建立考虑动态充电负荷需求的电动汽车充电负荷模型，分析电动汽车充电负荷在不同因素下的变化规律。

1 不确定充电行为建模及充电负荷计算方法

1.1 不确定充电行为建模方法

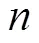
1.2 考虑动态充电负荷需求的充电负荷计算方法

假设电动汽车具有普通燃油汽车相似的驾驶特性，应用蒙特卡洛法建立充电负荷模型[13]，具体步骤如下：

1)基于大量车辆行驶数据，对电动汽车驾驶行为进行建模，如日行驶里程、开始行驶时刻、结束行驶时刻等，生成用户驾驶行为随机数。

冰臼的成因在中国地质科学院地质研究所韩同林教授出版的《发现冰臼》一书中有详细的论述，它是指古冰川融水沿冰川裂隙自上而下似滴水穿石的方式冲蚀基岩产生的，形成的机制参见图2[3]。

2 动态充电负荷模型的建立

对建模过程作如下规定：

(1) 电池每次充电都充满才停止；

(2) 充电过程始终为恒功率充电。

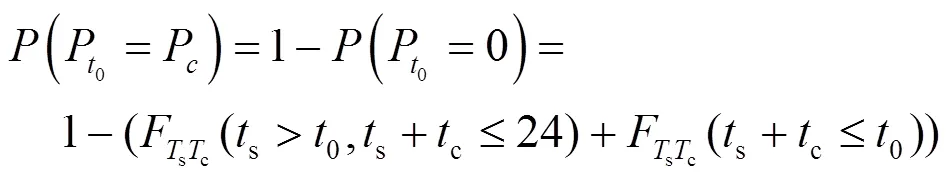
则考虑充电开始时刻与充电时长的充电功率即为所有电动汽车充电功率的时序分布，故考虑时序分布的充电功率的表达式为

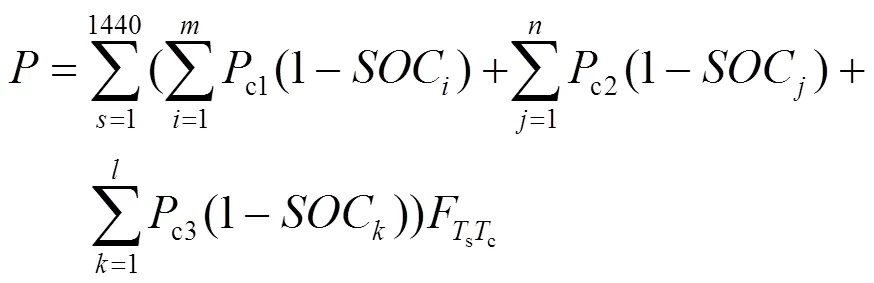
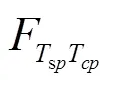
3 多种因素对动态充电负荷模型的影响

3.1 峰谷电价的影响

峰谷电价是电网公司为合理优化居民用电结构而实施的一项良性互动的价格鼓励机制。受峰谷电价影响的车主可以分为两类：第一类用户更看重谷电价带来的经济实惠，能够积极响应电力部门削峰填谷的需求，调整原始充电时间；第二类用户更在意自身用电与用车的舒适度，对峰谷电价不敏感，此类用户仍会根据实际需求无序充电。采用简化型两段式峰谷电价模型如公式(4)所示。

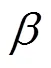
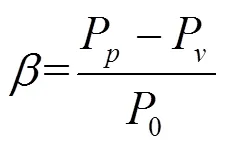
3.2 天气因素的影响

3.3 出行目的的影响

随着我国交通网络的进一步拓展，不同区域间的人口流动性变大，人们的出行目的也日渐多样化。从图1可看出，1994年通勤出行总量占全年出行量的近70%，2010年非通勤出行量首次超过通勤出行，成为汽车出行目标首位。但不能忽视的是，通勤出行仍然是人们出行目标不可缺少的一部分。故假设2020年，通勤出行量占全年总出行量的55%，非通勤出行占总出行量的45%。而由文献[15]及分析可知，通勤出行属于刚性出行，其出行需求不易改变，而非通勤出行的随机性较强，无明显规律，而出行目的主要影响的是私家车主的充电起始时间及选择何种充电方式，其次是出租车。故假设在通勤模式下，私家车常规充电与随机充电比例为4：1，出租车随机充电比例增加10%；而在非通勤模式下，私家车与公交车充电比例均降至80%，其中私家车常规充电与随机充电比例为3：2，出租车随机充电比例增加20%。

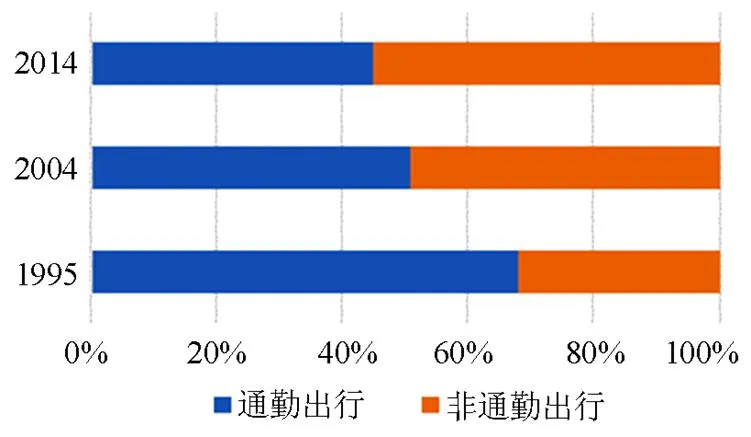
图1 汽车用户出行分布图

4 算例分析

采用上述模型对不同影响因素下南京市2020年电动汽车充电负荷进行测算，并分别对各因素的影响作用进行分析。

4.1 参数设置

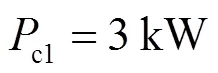
4.2 预测结果

根据前述分别考虑峰谷电价、天气条件和出行目的三种影响因素的动态充电负荷模型，以及相关计算参数的设置，采用蒙特卡洛模拟方法得到南京市2020年电动汽车充电负荷预测曲线如图2所示。

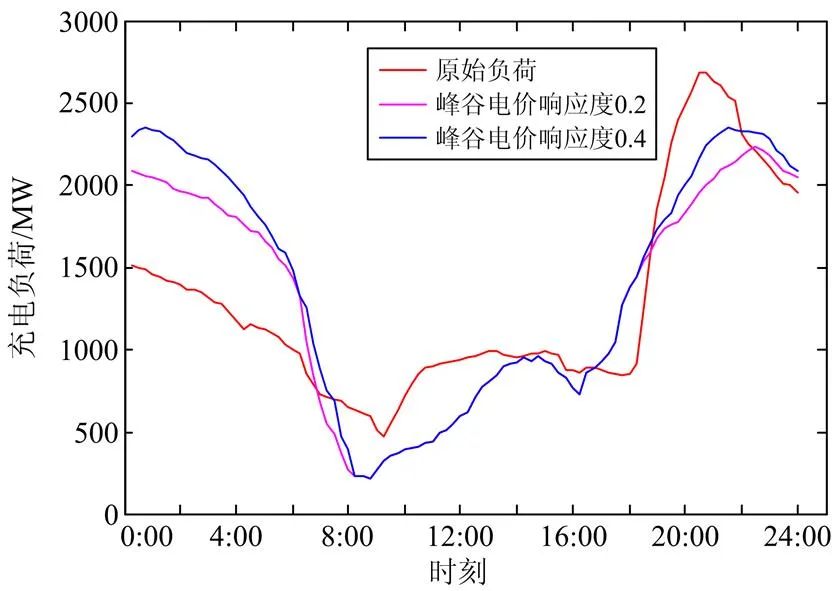
图2 峰谷电价政策下充电负荷预测曲线

4.3 结果分析

1) 由图2可以看出，峰谷电价机制下谷荷大幅提高，平期负荷略微下降，峰荷下降，且峰负荷出现时间向后推延。另外，用户响应度直接影响峰荷与谷荷的波动范围，用户响应度过低时，负荷变化不明显，随着响应度适度提高，整体负荷曲线趋于平缓。

2) 由图3可知，天气情况对电动汽车充电负荷的影响主要表现为幅值：天气情况较好时，凌晨0:00—6:00的充电负荷始终维持在1800 MW左右，遭遇恶劣气候时，负荷迅速跌落至1000 MW；此外，恶劣气候的负荷波动强于良好天气，峰谷值差异较大；另外，从18:00开始，良好天气下的充电负荷幅值是恶劣天气下的1.2倍，因此，良好天气下的充电负荷的负荷整体水平高于恶劣天气情况，而恶劣天气的充电负荷波动强于良好天气。

图3不同天气条件下充电负荷预测曲线

Fig. 3Charging load prediction curve under different weather conditions

3) 由图4可知，由于车主的出行目的不同，其充电负荷呈现不同特性。通勤模式下，充电负荷高峰时间段集中在0:00—6:00与18:00—21:00，在0:00与20:00呈现两次用电高峰，分别是1800 MW与2600 MW。相比通勤出行，非通勤模式下的充电负荷水平整体下降，峰值用电负荷仅相当于通勤模式下峰值负荷的80%，峰值负荷约为2000 MW；且全天负荷曲线相对平缓，仅在正午左右出现短时用电突增，而全天充电负荷高峰时间集中在0:00—6:00与20:00—23:00。由此可见，相比非通勤模式，通勤模式下的充电负荷日波动性更强，负荷水平更高，对电网的冲击也更大。

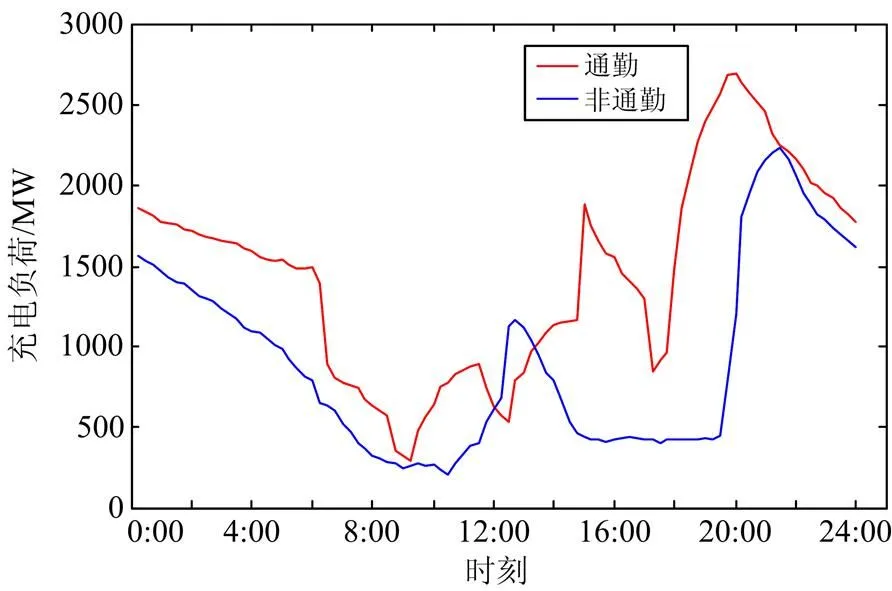
图4 不同出行目的下充电负荷预测曲线

5 结论

电动汽车充电负荷是一种变化快、分布规律不明显、波动幅度大的随机负荷，若在不清楚其变化特性的前提下接入，会给电网运行带来安全隐患。传统负荷建模方法忽略了充电负荷影响因素，将充电过程大致简化为理想过程，不能反映真实负荷变化规律。与常规充电负荷模型相比，考虑影响因素模型更能有针对性地分析具体因素的影响，仿真结果表明：峰谷电价机制下，负荷曲线的峰谷特性发生显著变化，谷荷上升，峰荷下降，这说明恰当的峰谷电价确实能够有效引导用户错峰充电，但平期负荷略有下降，需要谨防移峰风险；在不同天气条件下，晴好天气下的负荷水平略高于恶劣天气，主要表现在峰荷水平；在不同出行目的因素下，通勤出行下的负荷水平整体高于非通勤出行，且通勤负荷波动性更强，变化周期与典型通勤时间对应。

[1] 王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述[J]. 中国电机工程学报, 2013, 33(1): 1-10.

WANG Xifan, SHAO Chengcheng, WANG Xiuli, et al. Survey of electric vehicle charging load and dispatch control strategies[J]. Proceedings of the CSEE, 2013, 33(1): 1-10.

[2] Green II R C, WANG L F, ALAM M. The impact of plug–in hybrid electric vehicles on distribution network: a review and outlook[J]. Renewable and Sustainable Energy Reviews. 2011, 15(1): 544-553.

[3] 胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4): 1-11.

HU Zechun, SONG Yonghua, XU Zhiwei, et al. Impacts and utilization of electric vehicles integration into power systems[J]. Proceedings of the CSEE, 2012, 32(4): 1-11.

[4] 杨冰, 王丽芳, 廖承林. 大规模电动汽车充电需求及影响因素[J]. 电工技术学报, 2013, 28(2): 22-27.

YANG Bing, WANG Lifang, LIAO Chenglin. Research on power-charging demand of large-scale electric vehicles and its impacting factors[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 22-27.

[5] AYLOR J, MAITRA A, ALEXANDER M, et al. Evaluation of the impact of plug-in electric vehicle loading on distribution system operations[C] // Power &Energy Society General Meeting. Calgary, Alberta: Energy Development and Power Generation Committee, 2009.

[6] ROTERING N, ILIC M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1021-1029.

[7] 陈静鹏, 艾芊, 肖斐. 基于用户出行需求的电动电动汽车充电站规划[J]. 电力自动化设备, 2016, 36(6): 34-39.

CHEN Jingpeng, AI Qian, XIAO Fei. EV charging station planning based on travel demand[J]. Electric Power Automation Equipment, 2016, 36(6): 34-39.

[8] 贾龙, 胡泽春, 宋永华. 考虑不同类型充电需求的城市内电动汽车充电设施综合规划[J]. 电网技术, 2016, 40(9): 2579-2587.

JIA Long, HU Zechun, SONG Yonghua. An integrated planning of electric vehicle charging facilities for urban area considering different types of charging demands[J]. Power System Technology, 2016, 40(9): 2579-2587.

[9] 罗浩成, 胡泽春, 张洪财. 环境温度对电动汽车充电负荷的影响分析[J]. 电力建设, 2015, 36(7): 69-74.

LUO Haocheng, HU Zechun, ZHANG Hongcai.Effect analysis of ambient temperature on electric vehicle charging load[J].Electric Power Construction, 2015, 36(7): 69-74.

[10] 陈丽丹, 聂涌泉, 钟庆. 基于出行链的电动汽车充电负荷预测模型[J]. 电工技术学报, 2015, 30(4): 216-225.

CHEN Lidan, NIE Yongquan, ZHONG Qing. A model for electric vehicle charging load forecasting based on trip chains[J].Transactions of China Electrotechnical Society, 2015, 30(4): 216-225.

[11] 杨冰, 王丽芳, 廖承林, 等. 不确定充电习惯对电动汽车充电负荷需求及充电负荷调节的影响[J].电工技术学报, 2015, 30(4): 226-232.

YANG Bing, WANG Lifang, LIAO Chenglin, et al.Effects of uncertainty charging habits on electric vehicles’ charging load demand and the charging load regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 226-232.

[12] 杨少兵, 吴命利, 姜久春, 等. 电动汽车充电站负荷建模方法[J]. 电网技术, 2013, 37(5): 1190-1195.

YANG Shaobing, WU Mingli, JIANG Jiuchun, et al. An approach for load modeling of electric vehicle charging station[J].Power System Technology, 2013, 37(5): 1190-1195.

[13] 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42.

LUO Zhuowei, HU Zechun, SONG Yonghua, et al. Study on plug-in electric vehicles charging load calculating[J].Automation of Electric Power Systems, 2011, 35(14): 36-42.

[14] 南京汽车拥有量突140万辆[EB/OL]. [2014-03-11]. http://www.xici.net/d200121762.htm,

[15] 南京上半年净增汽车17万辆[EB/OL]. [2014-07-16]. http://jsnws.jschina.com.cn/system/2014/07/16/021403956.shtml.

Electric vehicle charging load model considering dynamic charging load demand and multi factors

KE Huimin1,2, SHAO Junjun1, 2,SHI Jinyong1, 2

(1. NARI Group Corporation, Nanjing 211116, China; 2. NARI Technology Development Co., Ltd., Nanjing 211116, China)

Considering the uncertainty of charging load demand, this paper analyzes the effect mechanism of several important factors on charging load. This paper presents an electric vehicle charging load model based on the dynamic load demand of electric vehicle, which takes into account the influence of Peak-Valley price, weather conditions and travel destination. Taking the electric vehicle charging load in Nanjing city as an example of Monte Carlo analysis. The simulation results show that, under the Peak-Valley price mechanism, the valley load is greatly improved, the peak load is decreased and the peak load time is delayed; and under the condition of good weather, the overall load level is higher than that of bad weather, but the fluctuation of charging load in bad weather is greater than that of the good weather; and the overall load level of commuting mode is higher than that of non-commuting mode, and the load level fluctuates with typical commuting time.

dynamic charging load; peak-valley price; weather conditions; travel purpose

2017-08-20

柯慧敏(1990—)，女，硕士，助理工程师，研究方向为电动汽车充换电技术；E-mail: kehuimin@sgepri.sgcc.com.cn邵军军(1991—)，男，通信作者，硕士，研究方向为电动汽车与电网互动；E-mail: 1551428581@qq.com石进永(1987—)，男，本科，助理工程师，研究方向为电动汽车充电技术。E-mail: shijinyong@sgepri.sgcc.com.cn

江苏省科技厅项目(BE2015004-1)