基于Lyapunov函数的三电平SAPF控制策略
2017-03-17于佳琪李勇曹一家于晶荣徐勇
于佳琪+李勇+曹一家+于晶荣+徐勇

摘 要:提出了一种基于Lyapunov函数的三相中点箝位型三电平并联有源电力滤波器(Neutral-Point Clamped Shunt Active Power Filter,NPC-SAPF)的控制策略.建立了NPC-SAPF的数学模型并在此基础上构建包含输出电流和直流电压误差项的能量函数;进一步推导出关于控制增益的特征方程,并绘制出其三维函数图,结合Lyapunov大范围渐进稳定条件和系统极点位置得到控制增益选取范围,在此区间选取合适的控制参数,保证系统在不同负载类型下动态和稳态性能.针对NPC特有的中点电位平衡问题,采用连接直流电压中点与配电变压器中点并引入中性点电位误差反馈控制的方法实现中点电位平衡.对电压源型和电流源型这两类非线性负载的动态和稳态性能进行了仿真和实验,结果表明:该控制策略对电流型和电压型非线性负载均取得较好的谐波补偿效果.
关键词:三电平;并联有源电力滤波器;Lyapunov函数法;电能质量
中图分类号:TM615;TP273 文献标志码:A
Lyapunov-function-based Control Strategy for Three-level SAPF
YU Jiaqi1, LI Yong1, CAO Yijia1, YU Jingrong2, XU Yong1
(1.College of Electrical and Information Engineering, Hunan University, Changsha 410082, China;
2. School of Information Science and Engineering, Central South University, Changsha 410083,China)
Abstract:A Lyapunov-function-based control strategy for NPC-SAPF was proposed. The mathematical model of NPC-APF was built, and Lyapunov energy function including the tracking error of compensation currents and DC voltage was also constructed. Characteristic equation including control permanents was derived and plotted. Linear range of control permanents were also obtained after the overall consideration of system globally asymptotically stable conditions and pole location. Error feedback control technique was then utilized to keep neutral point potential balanced. In order to verify the compensation performance of the proposed current control scheme, nonlinear loads including diode bridge rectifier with an inductive load and a capacitive load was simulated and tested. Simulation and experimental results show that the proposed control strategy is effective in the nonlinear loads of both current-source type and voltage-source type.
Key words: three-level technology; shunt active power filter; Lyapunov functions; power quality
并聯有源电力滤波器(Shunt Active Power Filter, SAPF)是用于抑制谐波、提高电能质量的有效手段之一[1-2].其中,三相中点箝位型并联有源电力滤波器(Neutral-Point Clamped, NPC-SAPF)与两电平APF相比具有系统容量大、补偿效果好、经济成本低等优点,受到了研究者的青睐.
然而由于NPC-SAPF系统是一个高阶强耦合的非线性系统,采用非线性控制器会取得更好的稳定性和指令跟踪控制效果.近年来,许多学者将非线性理论应用于APF控制系统的设计中[3-5].文献[3]提出基于滑模控制的混合型APF,该控制策略虽能获得较好的补偿效果,但其存在高频抖动的现象.文献[4]提出自适应无源性控制方法,补偿效果较好,但无源性控制易受参数及外界扰动影响.文献[5]针对速度、负载力矩变动的直流电机驱动装置提出基于神经网络的APF控制方法,取得一定效果,但控制器设计相对复杂.基于Lyapunov稳定性理论的函数构造法作为非线性理论的基本方法,已应用于两电平APF控制,但在三电平NPC-SAPF上尚无应用[6-9].文献[6]提出一种基于Lyapunov的单相APF电流控制方法,其控制增益选取是通过数学构造得到输出电流和直流电压的稳定范围,进而确定控制增益的极值.文献[7]采用同样的方法应用于三相两电平APF中.文献[9]提出将Lyapunov方法应用于混合型APF中,其控制增益取值需通过在线优化的方法得到,这增加了系统响应时间,影响了系统的动态性能.
由于三电平APF状态变量多,采用数学构造的方法确定控制参数过程复杂、计算难度大.本文根据NPC-SAPF的数学模型推导出关于控制增益的特征方程,并绘制出其三维函数图,结合系统动态和稳态性能得到控制增益选取范围,从而保证了系统在不同负载类型下的动态和稳态性能.最后通过仿真和实验验证了采用Lyapunov函数法的NPC-SAPF补偿电流源型和电压源型非线性负载的有效性.
1 系统模型
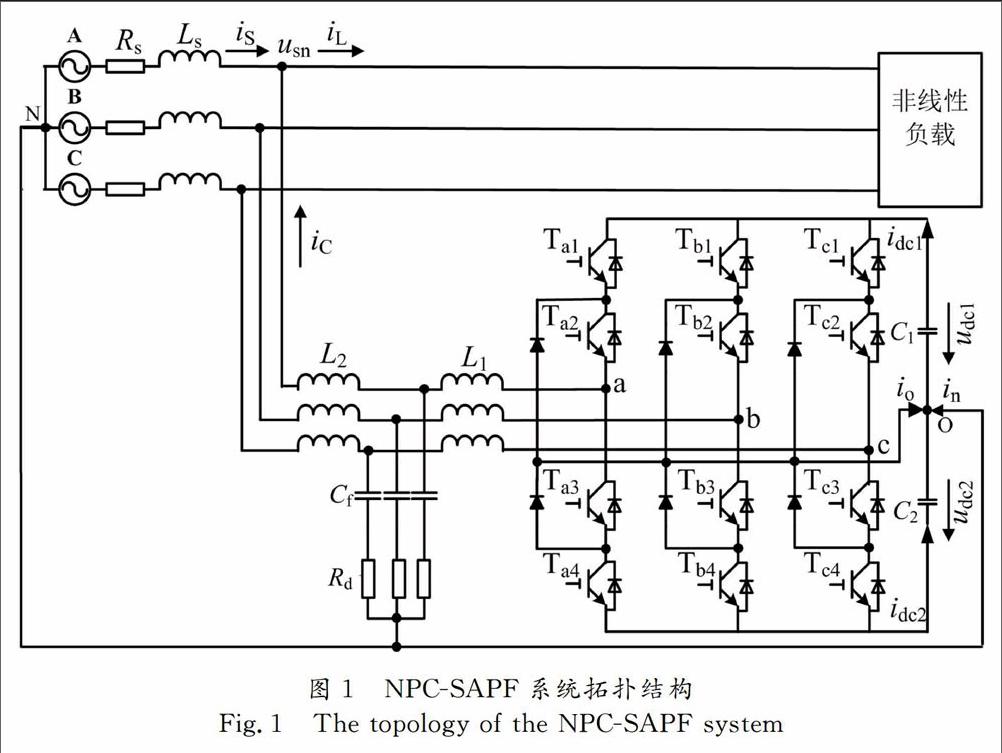
NPC-SAPF系统拓扑结构如图1所示,它是由电网电源、非线性负载、中点箝位型并联有源电力滤波器组成.
图1中,usn为公共耦合点电压;Ls和Rs分别为电网等效电感和电阻;L1,L2,Cf,Rd分别为输出滤波器逆变器侧电感、网侧电感、滤波电容及阻尼电阻;C1和C2为直流侧裂解电容,udc1和udc2为裂解电容上的电压;iS,iL,iC分别为电网电流、负载电流和输出电流.
由于每相桥臂功率器件的开关函数互补,且只有2个IGBT同时处于导通状态,定义开关函数Sx1和Sx2(x= a, b,c)为:
Sx1=1,Tx1和Tx2导通
0,Tx2和Tx3导通或Tx3和Tx4导通
Sx2=1,Tx3和Tx4导通
0,Tx1和Tx2导通或Tx2和Tx3导通 (1)
图1中的LCL滤波器等效为电感L,其中L=L1+L2.根据图中电压电流方向、基尔霍夫定律、和Park变换推导出NPC-SAPF在d-q旋转坐标系下以开关函数Sy1和Sy2(y= d, q)为控制输入的数学模型为:
dicddt=1L(usnd-Sd1udc1+Sd2udc2-Rficd+ωLicq)dicqdt=1L(usnq-Sd1udc1+Sd2udc2-Rficq-ωLicd)dudc1dt=1Cd(Sd1icd+Sq1icq)dudc2dt=-1Cd(Sd2icd+Sq2icq)(2)
式中:ω为电网电压角频率;L为输出滤波器的等效电感;Rf为电感的内阻;Cd为直流侧裂解电容值C1=C2=Cd;usnd,usnq,icd,icq分別为电网电压和输出电流的d轴和q轴分量.
2 控制策略
2.1 基于Lyapunov函数的控制器设计
根据Lyapunov稳定性理论和系统数学模型(式(2)),设能量函数F(x, t)为:
F(x,t)=12Lx21+12Lx22+12Cdx23+12Cdx24 (3)
其中状态变量x1,x2,x3,x4定义为:
x1=icd-i*cd,x2=icq-i*cq
x3=udc1-u*dc1,x4=udc2-u*dc2(4)
式中:i*cd和i*cq为在d-q坐标系下的参考电流,是采用滑动离散傅立叶变换(Slide-DFT)从iLabc中分离出来的;u*dc1和 u*dc2为直流侧裂解电容的参考电压,其值均为400 V.
当系统工作在稳态时,直流电压和输出电流均为对应的参考值:udc1= udc2 = u*dc=400 V,icd= i*cd,icq= i*cq;设稳态下的开关函数为Sd1,Sd2,Sq1,Sq2.结合式(2),可得稳态数学模型为:
Sd1-Sd2=1u*dc(usnd-Rfi*cd+ωLi*cq-Ldi*cddt)Sq1-Sq2=1u*dc(usnq-Rfi*cq-ωLi*cd-Ldi*cqdt)du*dc1dt=1Cd(Sd1i*cd+Sq1i*cq)du*dc2dt=-1Cd(Sd2i*cd+Sq2i*cq)(5)
本文采用SPWM载波层叠调制,为保持开关函数的对称性,稳态开关函数选择为:
Sd1=0.5(Sd1-Sd2)Sd2=-0.5(Sd1-Sd2)Sq1=0.5(Sq1-Sq2)Sq2=-0.5(Sq1-Sq2) (6)
结合式(2),(5),(6)和4个状态变量,可得NPC-SAPF最终的状态方程为:
dx1dt=1L(-Sd1(x3+u*dc1)+Sd2(x4+u*dc2)-
Rfx1+ωLx2)+u*dc1L(Sd1-Sd2)dx2dt=1L(-Sq1(x3+u*dc1)+Sq2(x4+u*dc2)-
Rfx2-ωLx1)+u*dc1L(Sq1-Sq2)dx3dt=1Cd(Sd1(x1+i*cd)+Sq1(x2+i*cq)-
Sd1i*cd-Sq1i*cq)dx4dt=-1Cd(Sd2(x1+i*cd)+Sq2(x2+i*cq)-
Sd2i*cd-Sq2i*cq)(7)
则能量函数F(x, t)的导数为:
dF(x,t)dt=-Rf(x21+x22)+
(Sd1-Sd1)(x3i*cd-x1u*dc)+
(Sd2-Sd2)(x1u*dc-x4i*cd)+
(Sq1-Sq1)(x3i*cq-x2u*dc)+
(Sq2-Sq2)(x2u*dc-x4i*cq)(8)
显然,式(8)中的第一项总是为负,为保证F(x, t)的导数一直负定,选取开关函数:
Sd1=Sd1+α(x3i*cd-x1u*dc)Sd2=Sd2+α(x1u*dc-x4i*cd)Sq1=Sq1+β(x3i*cq-x2u*dc)Sq2=Sq2+β(x2u*dc-x4i*cq)(9)
式中:α和β分别为d轴和q轴的控制增益,其值均小于0,为保持dq轴控制上的对称性,令α=β.
2.2 控制参数选取办法
由系统状态方程可推导出其雅克比矩阵Y:
Y=
-Rf+2αu*dcLωdl+αi*dc-Ld2-αi*cdu*dcL
-ω-Rf+2αu*2dcLq1+αi*cqu*dc-Lq2-αi*cqu*dcL
d1-αi*cdu*dcCdq1-αi*cqu*dcCdα(i*2cd+i*2cq)Cd0
d2+αi*cdu*dc-Cdq2+αi*cqu*dc-Cd0α(i*2cd+i*2cq)Cd
系统特征方程为:f(s, α) = |sI - Y|.α的取值需要满足2个条件:1)为了保证能量导数负定,则需要α<0;2)为保证系统稳定,则其特征根均在s的左半平面.本文为了简化计算,将特征根的取值限定在s平面的负实轴上.图2为f(s, α)的三维图,可以看出α的取值需要在图2所示的线段AB上,在保证系统稳定性的前提下需兼顾系统的动态性能,当极
点沿线段AB越靠近s平面原点,系统的动态性能越好.综合考虑系统稳态补偿效果及动态性能,经过多次仿真确定本文α=-0.015.
2.3 中点电压平衡控制策略
NPC逆变器的中点电位平衡方法通常在调制层面修改开关状态实现,基于空间矢量调制的平衡方法往往引入大量的开关矢量,增加输出电流谐波含量,同时占用大量数字处理器的数据空间[10];基于载波调制的平衡方法侧重考虑优化调制波,满足电压平衡的同时却增加了输出电流的谐波畸变率[11].本文提出一种简单有效的中点电位平衡方法:通过连接直流电压中点与配电变压器中点并引入中性点电位差值反馈控制.该方法通过修改控制环而非调制策略,实现方便,同时保证了电压平衡和电流质量.根据图1中O点基尔霍夫电流定律得:
d(udc1-udc2)dt=1Cd(idc1-idc2)=1Cd(io+in)d(udc1-udc2)dt-1Cdin=
1Cd[(Sa2-Sa1)ica+(Sb2-Sb1)icb+(Sc2-Sc1)icc](10)
式(10)表明,可以将裂解电容电压误差调节量叠加到电流内环上实现中点电压平衡,具体见图3.
3 仿真研究
為了验证所提控制策略的有效性,采用Matlab/Simulink软件建立了NPC-SAPF系统仿真模型,仿真采用电流源型和电压源型非线性负载.系统主要仿真参数如表1所示,电流源型和电压源型非线性负载相关参数如表2所示.
3.1 中点电位控制策略验证
为验证所采用中点电位控制策略降低了电网电流中额外的高频谐波,对文献[11]和所提控制策略进行了仿真,仿真结果分别如图4和图5所示.
从图4和5可以看出,本文所提中点电位平衡方法的电网电流谐波含量更少,电网电流波形更加光滑,产生的高频谐波更少,电网电流THD也有所降低.
3.2 稳态时补偿效果仿真
3.2.1 电流源型非线性负载补偿仿真
负载为电流源型非线性负载的仿真波形如图6所示.负载电流和补偿后电网电流的频谱分析如图7所示.由图7可见,补偿前a相负载电流总谐波畸
变率为28.18%,补偿后a相电网电流总谐波畸变率为3.82%.仿真结果说明该控制策略对电流源型非线性负载有很好的补偿效果.
3.2.2 电压源型非线性负载补偿仿真
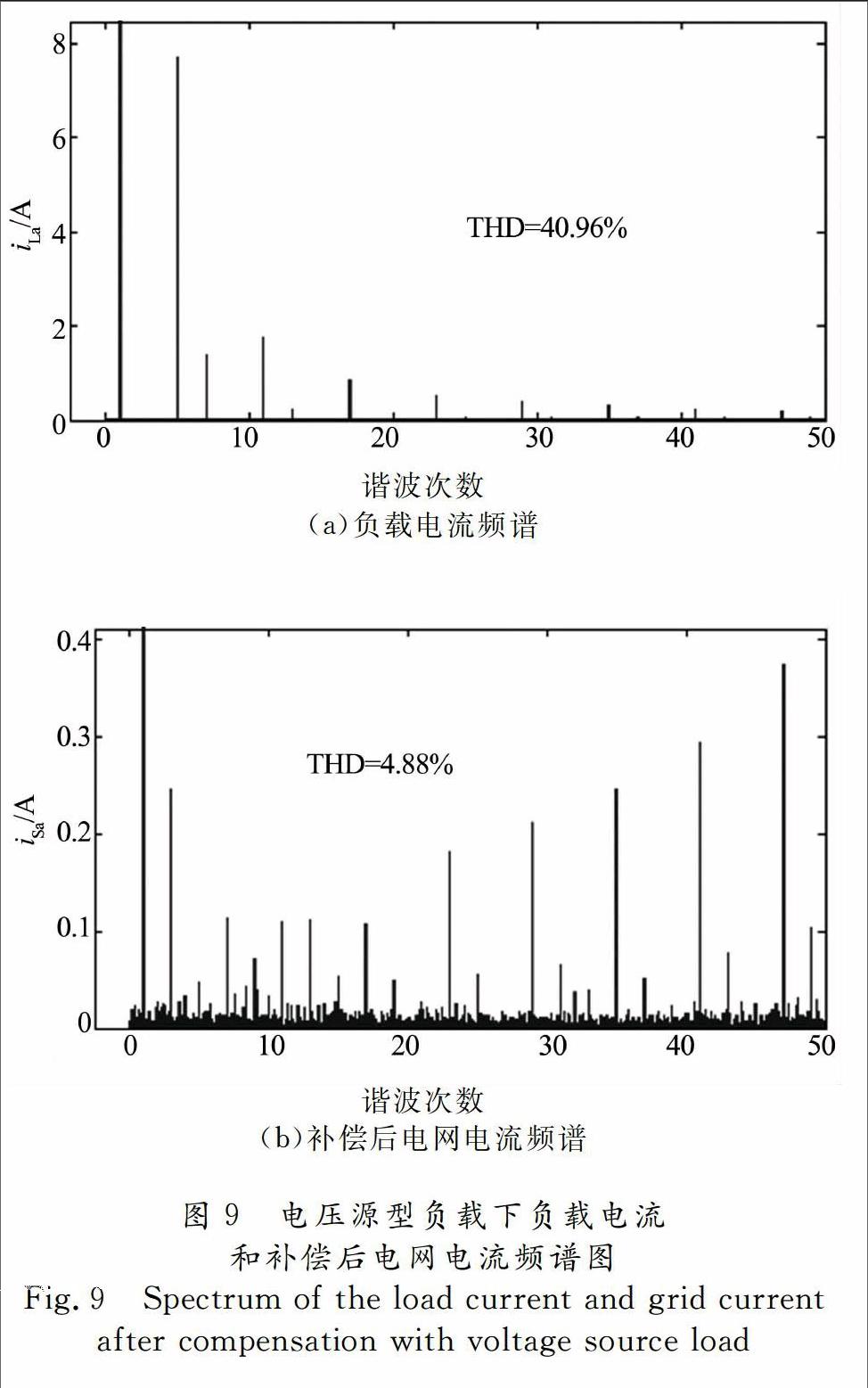
负载为电压源型非线性负载的仿真波形如图8所示.负载电流和补偿后电网电流的频谱分析如图9所示.由图9可见,补偿前a相负载电流总谐波畸变率为40.96%,补偿后a相电网电流总谐波畸变率为4.88%.由仿真结果可知,该控制策略对电压源型非线性负载同样具有较高的补偿精度.
3.3 负载变化时补偿效果仿真
3.3.1 电流源型非线性负载变化时补偿效果
为考察系统的动态性能,在0.3 s时电流源型负载中的Rdc由50 Ω变到25 Ω.图10为负载变化时APF的补偿情况,包括电网电流、负载电流、输出电流和电容电压波形.由图10可以看出,约1个周波后到达到新的稳态补偿,其间直流侧电容电压波动小于2 V,说明针对电流源型非线性负载,系统具有较好的动态跟踪特性.
3.3.2 电压源型非线性负载变化时补偿效果
在0.3 s时,将电压源型非线性负载的Rdc由50 Ω变到25 Ω.图11为负载变化时APF的补偿情况,由上到下分别是电网电流、负载电流、输出电流和电容电压波形.由图11可以看出,约1个周期后达到新的稳态补偿,其间直流侧电容电压波动小于2 V,说明针对电压源型非线性负载,系统同样具有较好的动态跟踪特性.
4 实验结果
为进一步验证所提控制策略的正确性和有效性,搭建了一台6.6 kVA NPC-SAPF样机,电流传感器采用 LA100-P型莱姆电流传感器,控制芯片采用DSP TMS320F28335,负载为三相不控整流桥加阻感和阻容型负载,相关参数如表1和表2所示.由于实验室示波器通道有限,实验结果仅包含a相.
4.1 稳态时补偿效果
图12为稳态时补偿电流源型和电压源型负载的实验结果.从图12(a)和图12(c)可以看出,补偿前负载电流波形与仿真一样,补偿后的电网电流波形呈理想正弦波状态,说明补偿精度很高.从图12(b)和图12(d)可以看出,两个裂解的直流电压稳定在参考值400 V.实验结果与仿真结果一致,表明了基于Lyapunov函数法的NPC-SAPF能有效治理电流源型和电压源型非线性负载产生的谐波.
4.2 负载变化时补偿效果
图13为电流源型和电压源型非线性负载变化时的实验结果.由图13(a)和图13(c)可知,电网电流在1个周期后达到了新的稳态;由图13(b)和图13(d)可知,直流电压波动平稳.实验结果表明本文所提控制策略对电流源型和电压源型非线性负载均有较好的动态跟踪特性.
5 结 论
本文提出基于Lyapunov函数法的三相中点箝位式有源电力滤波器控制策略.在NPC-SAPF数学模型的基础上,构建含输出电流和直流电压误差项的能量函数,结合系统动态和稳态性能确定控制参数选取范围,保证控制过程的收敛性和补偿性能;针对NPC特有的中点电位平衡问题,采用连接直流电压中点与配电变压器中点并引入中性点电位误差反馈控制的方法实现中点电位平衡.所提控制策略可以使系统在电流源型和电压源型非线性负载的情况下达到全局渐近稳定,同时获得较好的补偿效果.
参考文献
[1] 荣飞,罗安,涂春鸣.谐波电流检测新方法及在有源电力滤波器中的应用[J].湖南大学学报:自然科学版,2008,35(10):36-40.
RONG Fei, LUO An, TU Chunming. A new harmonic current detection algorithm and its application in active power filter[J].Journal of Hunan University: Natural Sciences, 2008,35(10):36-40. (In Chinese)
[2] 于晶荣,曹一家,关维德,等.基于FBD法的有源电力滤波器参考电流检测新方法[J].湖南大学学报:自然科学版, 2011, 38(2) : 45-50.
YU Jingrong, CAO Yijia, GUAN Weide, et al. A new reference current detecting algorithm based on FBD method for active power filter[J].Journal of Hunan University: Natural Sciences, 2011,38(2):45-50. (In Chinese)
[3] 郭伟峰, 武健, 徐殿国. 新型滑模控制的并联混合有源电力滤波器[J]. 中国电机工程学报, 2009, 29(27): 29-35.
GUO Weifeng, WU Jian, XU Dianguo. Hybrid shunt active power filter based on novel sliding mode control[J]. Proceedings of the CSEE, 2009, 29(27): 29-35.(In Chinese)
[4] 薛花, 姜建国. 并联型有源电力滤波器的自适应无源性控制方法研究[J]. 中国电机工程学报, 2007, 27(25): 114-118.
XUE Hua, JANG Jianguo. Study on adaptive passivity-based control strategies of shunt active filters[J]. Proceedings of the CSEE, 2007, 27(25): 114-118.(In Chinese)
[5] 吕征宇,钱照明, GREEN T C.并联有源电力滤波器的神经网络预测控制[J].中国电机工程学报,1999,19(12):22-26.
LV Zhengyu, QIAN Zhaoming, GREEN T C. A predicted control scheme of shunt active power filter with artificial neural network[J]. Proceedings of the CSEE,1999,19(12):22-26. (In Chinese)
[6] HASAN K, SMAN K. A new control strategy for single-phase shunt active power filters using a Lyapunov function[J]. IEEE Transactions on Industrial Electronics, 2006,53(1):305-312.
[7] 魏艷迪,张勇,程新功.基于李雅普诺夫函数的三相有源电力滤波器控制策略[J].电力自动化设备,2012,32(1):107-111.
WEI Yandi,ZHANG Yong,CHENG Xingong.Control strategy for three-phase APF based on Lyapunov function[J]. Electric Power Automation Equipment,2012, 32(1):107-111. (In Chinese)
[8] 侯世英,曾建兴,孙韬,等.基于李亚普诺夫稳定性分析的APF新型控制策略[J].电力自动化设备,2010, 30(10):33-37.
HOU Shiying, ZENG Jianxing, SUN Tao,et al. APF control strategy based on Lyapunov stability analysis[J]. Electric Power Automation Equipment,2010, 30(10): 33-37. (In Chinese)
[9] 韩伟,王大志,李云路,等.基于Lyapunov函数的混合型有源电力滤波器控制策略[J].控制理论与应用, 2014, 31(9):1174-1181.
HAN Wei,WANG Dazhi,LI Yunlu,et al. Lyapunov-function-based control strategy for hybrid active power filter[J]. Control Theory & Applications, 2014,31(9): 1174-1181. (In Chinese)
[10]CHOI U, LEE K. Simple neutral-point voltage control for three-level inverters using a discontinuous pulse width modulation[J]. IEEE Transactions on Energy Conversion,2013, 28(2):434-443.
[11]POU J, ZARAGOZA J, CEBALLOS S. A carrier-based PWM strategy with zero-sequence voltage injection for a three-level neutral-point-clamped converter[J]. IEEE Transactions on Power Electronics, 2012, 27(2):642-651.
