基于FIMD和小波变换电缆双端行波测距新方法

房俊龙，刘春涛，朱博文，魏新，张佳丽，李冬梅

（东北农业大学电气与信息学院，哈尔滨 150030）

基于FIMD和小波变换电缆双端行波测距新方法

房俊龙，刘春涛，朱博文，魏新，张佳丽，李冬梅

（东北农业大学电气与信息学院，哈尔滨 150030）

针对电力电缆故障定位误差较大问题，提出基于FIMD和小波变换模极大值导数双端行波测距新方法。利用PSCAD仿真软件建立电力电缆模型，变换各测量点电流突变量相模，分解变换后模分量FIMD。利用小波变换对分解所得IMF1分量求取模极大值导数，找出暂态信号奇异点。根据首个暂态行波奇异点，确定初始行波到达线路两端时间，计算故障距离。结果表明，该方法测定电缆故障距离精度高、具有应用可行性。

FIMD；小波变换；模极大值；行波测距；PSCAD

为满足用户供电需求及城市布局合理规划，电缆在城市供电系统中应用广泛。电力系统运行故障可能导致电力系统崩溃，影响正常供电。快速准确检测电力电缆故障点位置，及时消除故障，避免输电线路中电缆损坏，对电力系统安全稳定运行具有重要意义。

电力电缆故障测距主要采用行波法、脉冲法和阻抗法。行波法定位速度快、测距精度高且不受过渡电阻及线路参数影响，发展前景较好[1]，行波法分为单端行波测距法[2]和双端行波测距法[3]。束洪春等利用故障特征频带和TT变换对电缆单端行波测距，实现故障定位[4]但电缆行波色散较重，产生折射波和反射波影响行波时间测定；计算波速复杂，单端行波测距产生误差，测距精度降低。陈玉林等基于时频分量相关分析对电缆双端行波测距[5]，该方法受外界干扰影响小，可提取不同尺度下中心频率，完成故障测距，但易受线路参数影响，波速提取产生误差，测距精度降低。

为解决电力电缆传播过程中因线路参数、系统不稳定因素制约，电缆线路中行波波速测量难问题。本文利用快速本征模态分解算法（Fast intrinsic mode decomposition,FIMD）[6]，分解暂态行波信号，得到固有模态分量（Intrinsic mode decomposition, IMF）和残余量，提取分解IMF分量中IMF1分量（First intrinsic mode decomposition），由于IMF1具有较好完整性和较高能量，作为小波变换[7-8]特征信号，求取模极大值导数，快速检测暂态行波信号到达电缆双端时刻，实现电缆故障测距。通过故障点计算，提取故障点暂态行波到达电缆双端时间，结合故障时间与故障距离比例关系，确定电缆故障点。验证试验表明，结果可靠性强，可提高测距精度，具有应用前景。

1 电力电缆模型

建立电力电缆模型，采用电磁暂态仿真软件PSCAD/EMTDC[9-11]，线路参数采用Bergeron模型，35 kV双端输电线路网络见图1。

图1 电缆线路网络Fig.1Source impedances in the system

2 FIMD算法和信号奇异性检测

2.1 快速本征模态分解

快速本征模态分解是对非平稳信号实现实时分析自适应分解算法。为消除模态混叠现象，将原始信号快速分解成固有模态分量，结果唯一。该算法运行效率高、收敛性能好，对信号具有较强自适应分解能力和计算速率。计算步骤如下：

①假设分析信号为f(t)，计算被分析信号所有极值点R(t)，如公式（1）所示，式中t表示采样时刻，m表示分析信号极值点个数。

式中，t0、tj、tm-1分别表示第0、j、m-1个极值点所对应采样时刻。

②利用线性转换连接所有极值点作残余量r（t），如式（2）所示。

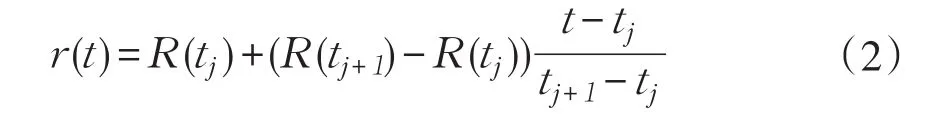
式中tj+1为第j+1个极值点对应采样时刻，0＜j＜m-1。

③从原始信号中去除残余量得到固有模态函数，修正固有模态函数，过程如下：

a.将当前IMF分量第i个极值点E(ti)作控制点，第i个控制点Pi坐标定义为

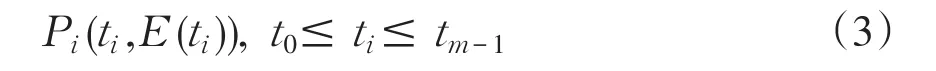
式中，ti为第i个极值点对应采样时刻。

b.定义第i个向量积为αi=Pi-1Pi×PiPi+1，依照相邻两向量积计算控制点中值。将控制点中值用三次样条连接作修正后残余量，利用原始信号减去修正后残余量即得到修正后IMF分量。

c.迭代上述过程，直到残余量极值点满足少于3个时结束分解计算。

④通过以上计算可将被分析信号f(t)分解成多个唯一IMF分量和1个残余分量。

2.2 小波变换检测信号奇异性

小波变换模极大值检测信号奇异性可快速识别奇异点，小波变换具有空间局部性，可“聚焦”信号局部特征结构。奇异点作为暂态信号重要特征，其奇异点与小波变换模极大值导数对应，用于检测电缆行波信号故障点。

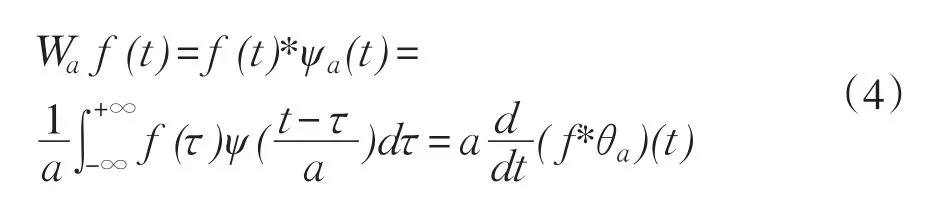
可见小波函数Waf(t)与函数f(t)及平滑函数θ(t)一阶导数乘积成正比，即变换一阶导数是电力系统[12-13]信号奇异点。因此，小波变换模极大值一阶导数可准确反映故障暂态信号信息。通过小波变换后不同尺度上综合表现反映暂态信号突变，检测暂态信号奇异点，确定行波信号到达电缆双端故障时间。

电力电缆故障信号表现为突变、非平稳信号，需对特定尺度上信号运用小波变换，时频分析，提取具有紧支撑性、正则性及带通滤波性能瞬时信号，准确检测电缆故障中奇异点，提高测距精度。因此，本文选择的小波基为Daubechies3小波。

2.3 基于FIMD和小波变换结合行波波头检测

由于电流互感器采集的三相电流间存在互耦，需通过相模变换解耦。本文采用凯伦贝尔（Karenbauer）变换对三相电流解耦，选取故障后1/4周期行波信号解耦；设置系统中相角为15°，故障开始时间为0.1 s，故障持续时间为0.01 s，采样步长设置为0.1 μs，即采样频率10 MHz，设定过渡电阻Rg60 Ω，线路总长100 km，系统阻抗和线路参数见表1、2。以M端为例，运用MATLAB处理分析采集数据，选用解耦后α模电流分量FIMD分解，得到2个IMF分量和1个残余量，如图2所示。

表1 系统阻抗Table 1System impedances (Ω)

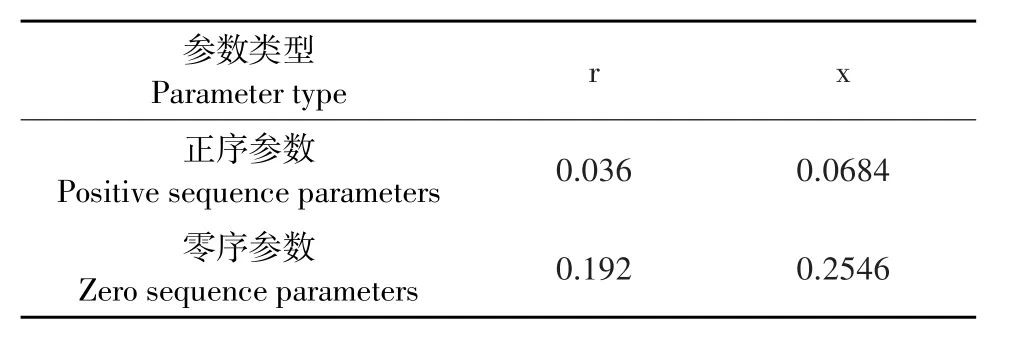
表2 电缆线路参数Table 2Cable line parameters(Ω·km-1)

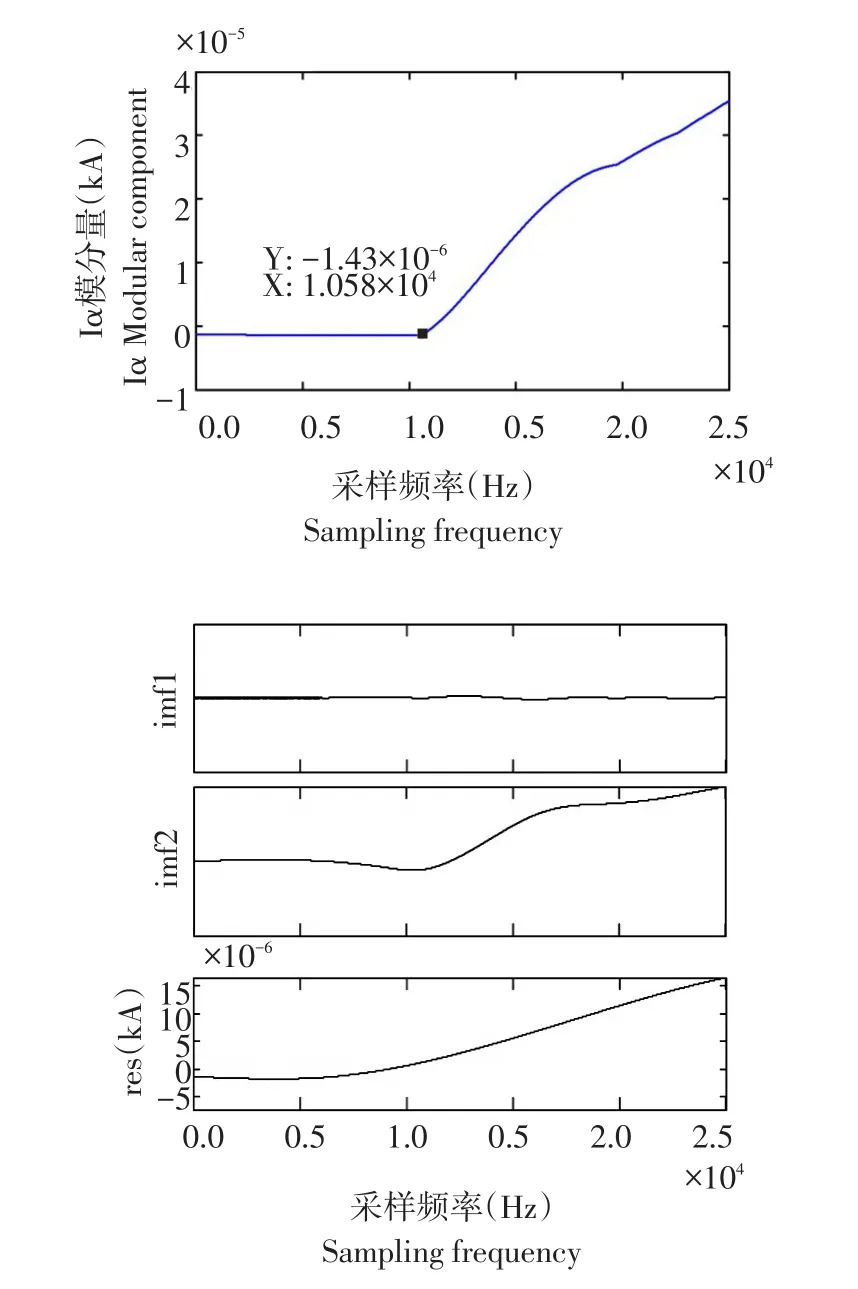
图2 α模电流及FIMD结果Fig.2α-mode current and the FIMD results

由图2可知，故障初始行波信号在1.058×104个采样点处开始突变，IMF1分量是初始行波分量，频率和能量最大，但随行波信号在线路中传输，能量减小，故选取IMF1电流分量作为求取小波变换模极大值首选。利用db3小波基，对IMF1电流分量4层分解，提取d3信号，由于d3信号与原信号相关性较强，以d3信号作为平滑函数，对其求一阶导数，检测故障信号奇异点。

IMF1小波变换一阶导数曲线见图3，可见1.058×104个采样点处开始突变，与初始行波信号到达时间一致。因此，IMF1电流分量经小波变换得一阶导数曲线首个奇异点，对应时刻即为故障行波到达时刻，说明两种算法结合可快速查找奇异点。

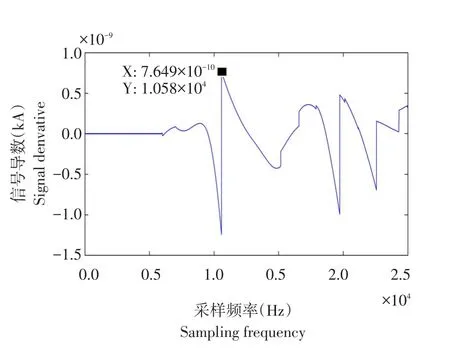
图3 IMF1小波变换一阶导数曲线Fig.3First order derivative curve of wavelet transform of IMF1

3 电缆线路双端行波测距算法分析

3.1 双端行波测距原理

双端行波测距算法利用故障点产生故障行波到达电缆线路两端时间，捕捉行波第一个波头，即可实现测距，不必对线路中反射波和折射波分析和考虑，且初始波波幅相对较大，便于区分，简化计算；对故障点和系统中波阻抗不连续点反射波，可精确实现故障测距，但须保证电缆双端时间同步性[14-15]。

虽然双端行波测距可解决单端行波测距问题，提高测距精度，保证测距准确性，但对故障时间精度要求很高，需双端时间同步并区分和识别故障点反射波与对端母线反射波，测距成本较高。

本文采用行波故障测距改进传统双端行波测距算法，无需检测故障点和输电线路中其他波阻抗产生的不连续点反射波，即可准确检测故障距离，不必测取线路故障中暂态电压或者电流行波信号到达线路两端时间及故障线路中波速可计算故障点；本文采用测距算法以传统行波测距为基础加以改进。改进的双端行波测距算法利用暂态行波到达线路两端第一个波头时间差测定故障点。由于故障点到达测量点距离只与行波传播时间有关，仅测量行波在线路中传播时间，即可确定故障点位置。双端测距主要原理见图4。

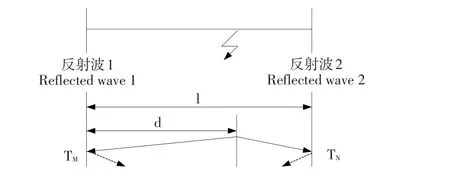
图4 双端行波测距原理Fig.4Schematic of double ended raveling wave fault location

本文采样时间与频率对应，测得采样频率是到达线路两端故障时间，利用故障时间计算故障距离，即故障点测距计算公式如下：

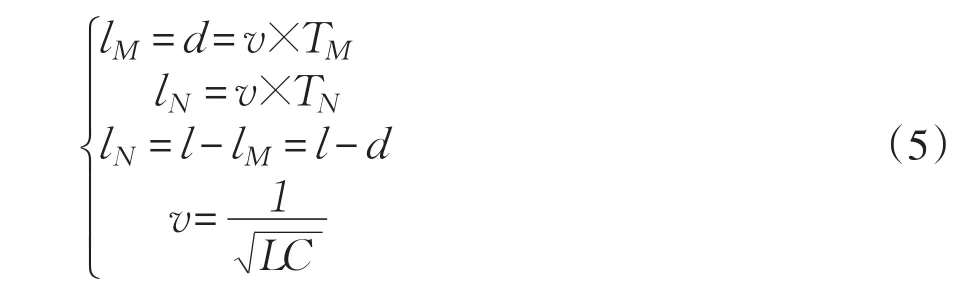
式中，TM、TN分别表示故障点到达M、N端故障时间，lM、lN分别表示故障点距M、N端距离，v是电缆在线路中传输速度，L、C分别表示电缆线路中电容和电感。

由上式（5）化简可得：

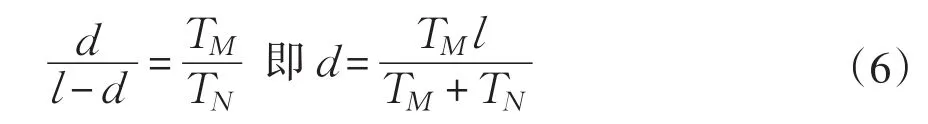
3.2 双端行波测距影响因素分析

电力电缆双端测距算法中，干扰因素影响测距，电缆线路发生故障后，瞬间产生1个突变暂态信号，用简单时频域分析法无法分析、判断这类信号。干扰因素影响故障行波信号采集，导致故障测距精度低。对测取电流信号FIMD分解，取IMF1分量，利用db3小波基小波变换，求得行波分量模极大值一阶导数。对故障开始时间设置为0.1 s，故障持续时间设置为0.05 s，其他不变，根据不同采样参数设定过渡电阻及故障距离。以单相接地短路故障对电缆测距产生影响因素说明，结果见图5。

由图5可知，随过渡电阻增大，故障电流幅值呈减小趋势，行波波头趋平滑，波头奇异性不明显；但不同过渡电阻，行波波头上升时间相同，行波波头起始点突变不变。行波测距受线路中其他因素影响小，只与自身因素有关。通过FIMD分解提取IMF1分量，运用小波分析去噪及重构信号，仍可获取有用暂态信息对故障点测距。

不同故障距离条件下α模电流分量及导数见图6，距离故障点越近，奇异点奇异性越强；但随故障距离增大，行波突变信号越弱，线路中故障点越远，可使线路中电流幅值更小，加其他信号干扰，故障点信号易被淹没。但对暂态信号采集影响小，即突出FIMD和小波变换模极大值结合优势。

综上所述，在电力电缆发生单相接地故障时，不同过渡电阻及不同故障位置，对电力电缆故障行波信息影响较小，只要检测出故障后暂态行波信息，结合FIMD和小波模极大值，即可检测出暂态行波故障奇异点，识别故障点位置。

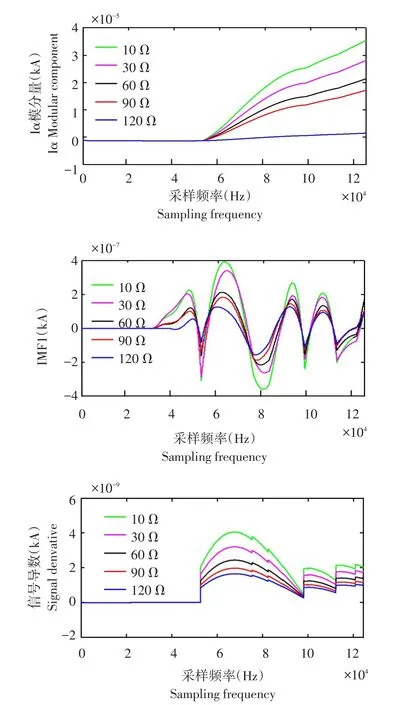
图5 不同过渡电阻下α模电流分量IMF1及导数Fig.5Component,IMF1 and derivative of the modelcurrent of different grounding resistance

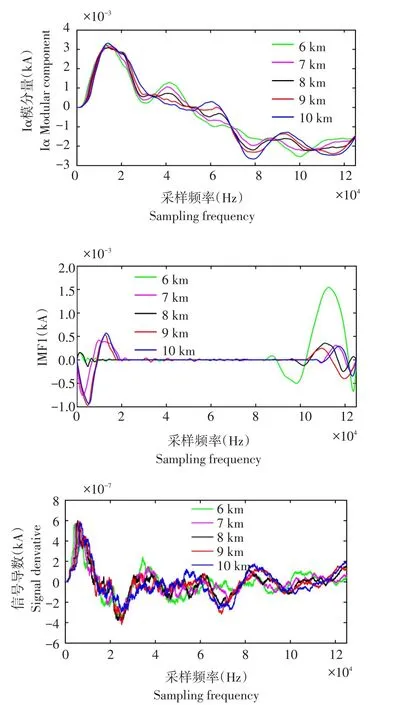
图6 不同故障距离下α模电流分量及导数Fig.6Component and derivative of α-mode current at different fault distance

3.3 双端行波测距仿真分析

为检测改进波测距算法，取解耦后1/4周期波形，设定故障距离为65 km，对故障后M、N端电流行波相模变换，运用FIMD提取IMF1分量，利用小波变换，提取不同故障条件下模极大值奇异点，对提取IMF1分量一阶求导数，结果见图7、8。

由图7、8可见，利用IMF1分量和小波模极大值导数，测得故障点到达M端初始行波时间为7.792×10-5μs，到达N端初始行波时间为4.210×10-5μs，利用公式（6）计算故障距离为64.9225 km，测量距离与设定故障距离65 km故障误差比为0.12%，误差在允许范围内。可见，利用FIMD分解的IMF1分量及小波变换模极大值导数可实现故障测距，及时检测故障点，提高故障测距效率。

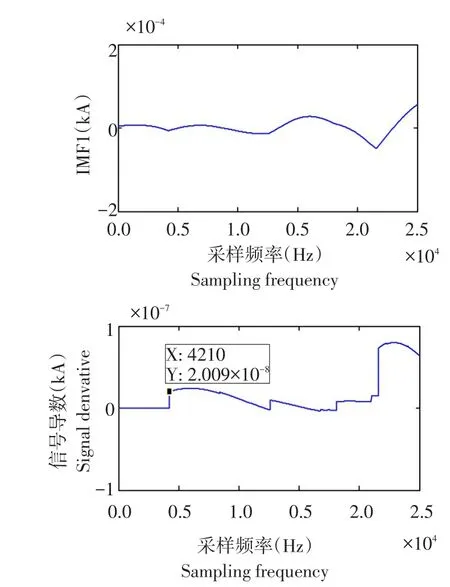
图7 M端IMF1电流分量及信号导数Fig.7Current component and signal derivative of M at IMF1

4 试验验证及对比分析

4.1 试验方案设计

为验证本算法稳定性和有效性，设计电缆双端行波故障定位装置试验，试验接线如图9所示。

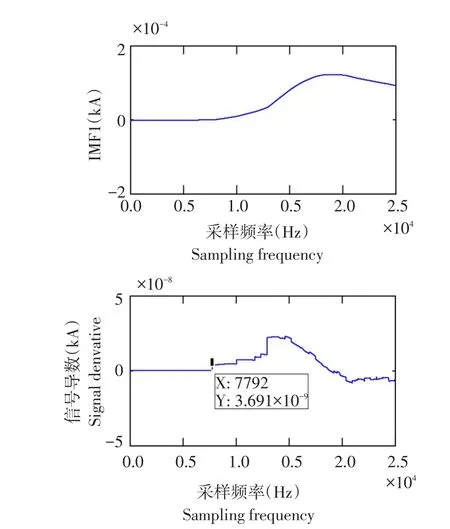
图8 N端IMF1电流分量及信号导数Fig.8Current component and signal derivative of N at IMF1

选用KHC911L型开合式电流互感器，型号参数为100-600A/5A，A/D转换芯片采用美国TI公司生产16位高性能模数转换芯片ADS8364，GPS为Trimble公司生产并行12通道跟踪、嵌入式GPS接收机，采用电流互感器校验仪，测量范围5A/1A～6300A/1A。

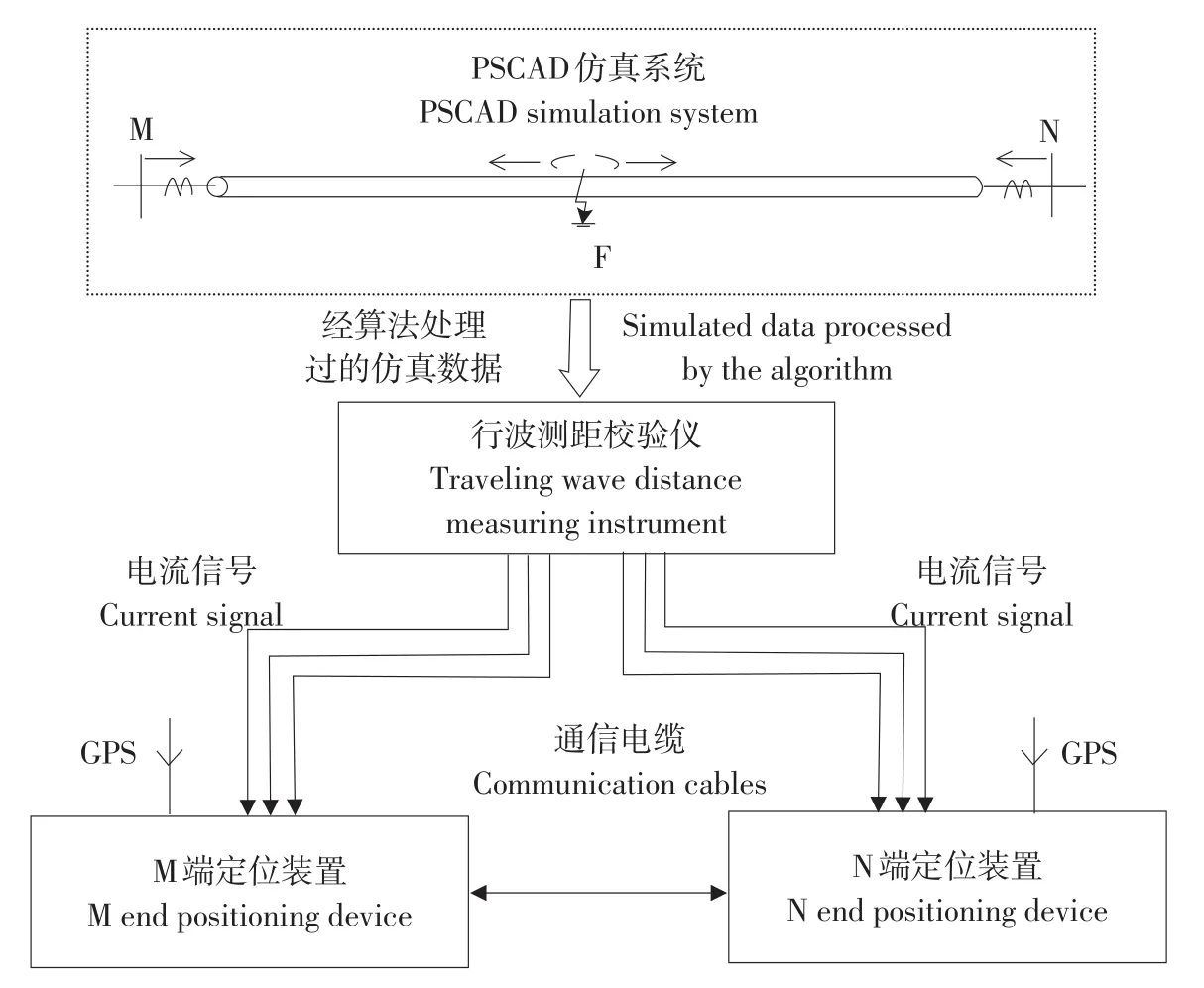
图9 电缆线路双端行波故障定位装置试验Fig.9Test of double-ended traveling wave fault location device on cable line

本试验电缆双端安装型号为KHC 911L型开合式电流互感器，采集电缆线路电流信号，对采集电流信号经前置处理器放大、整流及滤波处理，处理后数模转换，通过电缆两端GPS数据传输，发送到型号为ADS8364A/D转换器中，将转换后信号传输到核心系统装置DSP中，即TMS320F2812数据处理芯片（美国TI公司生产），通过串口电路将数据发送给上位机，对比分析采集电流信号，将故障点通过ADR-D2910GPRS型号网络模块发送，由于GPRS模块上安装GSM卡，具有信息群发功能，便于故障点维修，提高供电可靠性。

结合本文建立仿真模型及试验，利用行波测距校验仪不同按键设置不同故障距离和故障类型，通过PSCAD仿真模型计算获取电缆线路两端三相电流行波数据，将数据传输到行波测距校验仪中保存。在电缆故障测距中，其中A、B、C分别表示电缆线路三相，G为接地；对于单相接地故障、三相短路故障以及三相短路接地故障，采用α模、0模和β模电流分量分别测量，当线路发生两相短路或者两相接地短路故障时，若0模分量为两相故障，对其他两模分量混杂程度较小，而其他两模量因故障点电弧燃烧不稳定，α模和β模电流分量衰减较快，奇异点不明显，因此采用0模分量测距。以单相接地故障为例，得到M、N端暂态电流信号电流互感器校验仪产生波形图，结果见图10。

通过设定行波测距校验仪，选择不同故障类型产生暂态电流行波数据并输出相应电流信号，用于电缆双端行波故障定位装置试验。行波校验仪转化得到GPS测距时间，不同故障类型下计算故障距离结果见表3。

由表3可知，采用改进的双端测距算法相对误差＜0.7%，不同故障类型测距中精度随故障距离增加而提高，克服单端测距中折射波和反射波影响；试验结果和仿真结果基本一致，不同故障类型对测量精度影响较小，该算法不受电缆线路中波速影响，故采用本算法对电缆线路故障测距可行。

4.2 结果对比分析

双端行波测距与单端行波测距相比，双端行波测距可靠性和精确度更高（见表4）。以单相接地短路故障为例，其他参数保持不变，测距结果表明，两种算法均可测出故障点，但双端行波测距误差明显低于单端行波测距，可验证行波法电缆故障测距有效性。

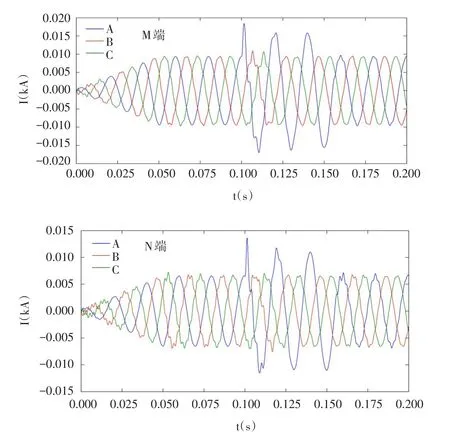
图10 M、N端暂态电流信号试验波形Fig.10M,N side transient current signal test waveform

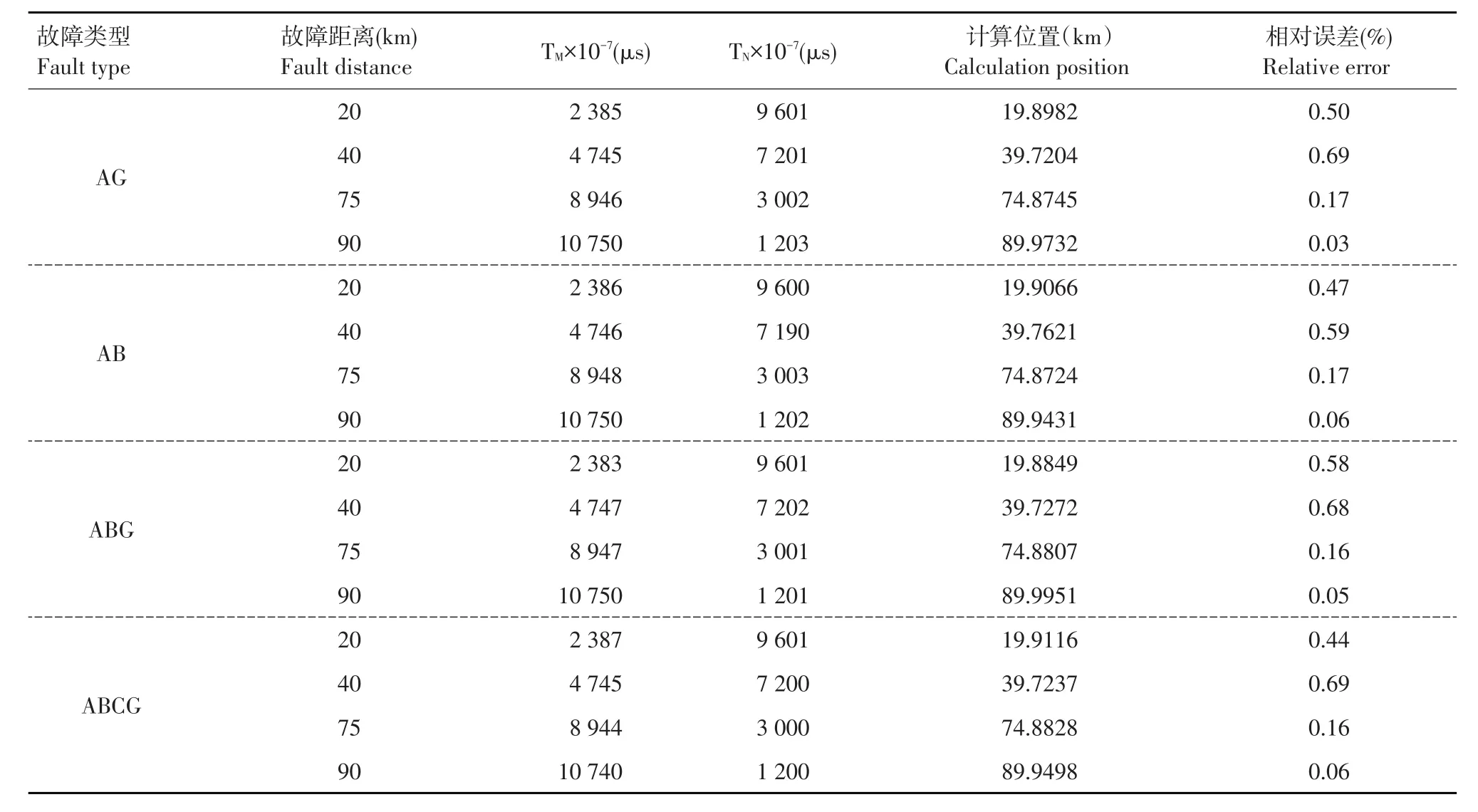
表3 不同故障类型故障测距Table 3Different fault types of fault location

表4 不同测距算法试验结果比较Table 4Comparison of simulation results of different ranging algorithms

5 结论

针对电力电缆线路行波测距精确度问题，本文提出基于FIMD和小波变换电力电缆双端行波测距新方法，结合本算法和试验验证，结论如下：

a.将FIMD算法和小波变换模极大值导数结合用于暂态行波波头奇异性检测，可快速准确检测故障初始行波到达电缆双端时间，提高故障检测效率。

b.改进双端行波测距法与电缆线路传播速度无关，可消除波速造成误差，不受线路参数影响，更具实用价值。

c.本试验方法可确定故障行波到达测量端准确时间及故障点位置，简单易行，测距精度高。

[1]郑州,吕艳萍,王杰,等.基于小波变换双端行波测距新方法[J].电网技术,2010,34(1):203-207.

[2]曹晶,曾祥军,杨毅,等.单-多端行波组合架空线配电网单相接地故障定位方法[J].电测与仪表,2015,52(16):32-37.

[3]周湶,卢毅,廖瑞金,等.基于小波包提取算法和相关分析电缆双端行波测距[J].电力系统保护与控制,2012,40(1):1-4.

[4]束洪春,田鑫萃,董俊,等.利用故障特征频带和TT变换电缆单端行波测距[J].中国电机工程学报,2013,33(22):103-112.

[5]陈玉林,陈允平,龚庆武.基于时频分量相关分析高压电缆双端行波测距[J].电力自动化设备,2008,28(12):16-20.

[6]范新桥,朱永利.基于双端行波原理多端输电线路故障定位新方法[J].电网技术,2013,37(1):261-269.

[7]徐淑琴,雷兴元,刘宇佳,等.基于时间序列与小波分析耦合模型区域降雨量预测研究[J].东北农业大学学报,2015,46(11):63-69.

[8]柴玉华,王蓉,高延英.基于小波变换图像融合算法实现[J].东北农业大学学报,2005,36(5):628-631.

[9]杨关春,陈平,高鹏.基于PSCAD单芯低压电缆故障暂态仿真建模[J].山东大学学报,2013,27(2):50-53.

[10]鹿洪刚,覃剑,陈祥训.35kV电力电缆在线故障测距仿真研究[J].电网技术,2008,32(24):81-87.

[11]邢海瀛,袁汉川,邓春,等.基于分布参数电力电缆故障定位新型算法研究[J].电力系统保护与控制,2011,39(14):16-20.

[12]Li S B,Zhao Y L,Li J C et al,Fault line selection method considering grounding fault angle for distribution network[J].Journal of Northeast Agricultural University:English Edition,2015,22(1): 58-65.

[13]Fang J L,Xing Y,Fu Y,et al,Rural power system load forecast based on principal component[J].Journal of Northeast Agricultural University:English Edition,2015,22(2):67-72.

[14]向强铭,王茜,陈靖秋,等.基于奇异值分解理论双端行波故障测距研究[J].电力系统保护与控制,2014,42(12):14-18.

[15]陈德超,李鸿,韩聪.基于谐波电力电缆单相接地故障在线测距方法研究[J].电力学报,2014,29(3):193-196.

New two-terminal cable traveling wave fault location method based on

FIMD and wavelet transform

FANG Junlong,LIU Chuntao,ZHU Bowen,WEI Xin,

ZHANG Jiali,LI Dongmei(School of Electrical and Information,Northeast Agricultural University,Harbin 150030,China)

In view of the poor accuracy in present power cable fault location methods,a novel fault location method based on the principle of two-terminal traveling wave was applied to fault location for power cable,the fault location based on fast intrinsic mode decomposition and wavelet transform modulus maxima derivative.Firstly,PSCAD was applied to establish the simulation model of power cable,Phase-to-phase transformation of the measurement point current was carried out,the current component of the measuring point was decomposed by fast intrinsic mode decomposition(FIMD).secondly,the wavelet transform was applied to extract the modulus maxima of the first intrinsic mode decomposition(IMF1)component,and the first derivative was obtained by the modulus maxima,found the singularity of the transient signal.finally,the time of the initial traveling wave arrived at the double-ended of the line,according to the first transient traveling wave,and calculated the fault distance.Result of PSCAD based on test show that the proposed method was of high location accuracy and feasibility.

FIMD;wavelet transform;modulus maximum;traveling wave;PSCAD

TM773

A

1005-9369（2017）01-0065-08

2016-07-08

国家科技支撑计划项目子课题（2014BAD06B04-1-09）

房俊龙（1971-），男，教授，博士生导师，研究方向为电力系统自动化。Email:junlongfang@126.com

时间2017-1-9 15:46:09[URL]http://www.cnki.net/kcms/detail/23.1391.S.20170109.1546.018.html

房俊龙,刘春涛,朱博文,等.基于FIMD和小波变换电缆双端行波测距新方法[J].东北农业大学学报,2017,48(1):65-72.

Fang Junlong,Liu Chuntao,Zhu Bowen,et al.New two-terminal cable traveling wave fault location method based on FIMD and wavelet transform[J].Journal of Northeast Agricultural University,2017,48(1):65-72.(in Chinese with English abstract)