光伏电池输出特性及其最大功率跟踪研究

李 勇，程汉湘，陈杏灿，余 音

(1.广东工业大学自动化学院，广东 广州 510006； 2.中国移动通信集团广东有限公司广州分公司，广东 广州 510000； 3.广东电网有限责任公司东莞供电局，广东 东莞 523008)

光伏电池输出特性及其最大功率跟踪研究

李 勇1，程汉湘1，陈杏灿2，余 音3

(1.广东工业大学自动化学院，广东 广州 510006； 2.中国移动通信集团广东有限公司广州分公司，广东 广州 510000； 3.广东电网有限责任公司东莞供电局，广东 东莞 523008)

介绍了光伏电池工程实用数学模型，分析了光伏电池在任意温度和光照强度下的U-I、U-P输出特性。对扰动观察法进行改进并建立了最大功率跟踪模型(MPPT)，与Buck-Boost电路结合使用通过PWM来获得控制信号以此来改变光伏电池的输出电压，能很好地实现光伏发电系统最大功率点的跟踪。最后运用Matlab的Simulink 搭建了光伏电池仿真模型。仿真结果得出：虽然当光照强度稳定时，温度越高最大输出功率越小，当温度恒定时，光照强度越大最大输出功率越大；但当温度和光照强度同时变化时，起主要影响因素的依然是光照强度。仿真验证了改进扰动观察法比电导增量法更快速而精准地将输出功率稳定在一个固定值，为整个光伏及微网系统进一步研究提供参考价值。

数学模型；输出特性；扰动观察法；MPPT；Buck-Boost

0 引 言

随着不可再生能源的消耗，全球均在面临着能源危机，而太阳能依靠其清洁、可再生以及分布广泛等特点成为如今第二位快速发展的能源系统[1]。更高效地利用光伏电池所吸收的能量，提高光伏电池对能量的转换效率，降低光伏发电产品的制造成本是光伏发电系统得到广泛应用的首要问题[2，3]。因此最大功率点的提出与跟踪成为光伏发电的首要问题[4]。

文献[5]介绍了基于恒定电压法(CVT)的最大功率点跟踪，该方法优点在于成本低、控制简单、易于实现、系统不易出现振荡、可靠性高。但缺点在于误差大、控制精度差、忽略了温度的影响。文献[6]采用了扰动观察法，此方法为自寻优过程，算法简单易于实现。然而在实际应用中光照强度和温度是按一定规律改变的，当变化的速度较快时很容易产生误跟踪。文献[7]采用了电导增量法，虽然弥补了上面两种方法的不足，但这种控制方法粗略地认为光伏电池输出电压也就是负载两端电压，而且其步长为固定的增量，在寻优的过程中需要花费较长的时间，影响光伏电池的工作效率。为了提高最大功率跟踪的快速性和准确性，文章在传统的扰动观察法的基础上加以改进，增加了Buck-Boost电路，并采用适当调整占空比步长搜寻最大功率点。

1 光伏电池的基本原理

光伏电池工程应用等效电路图如图1所示[8]。

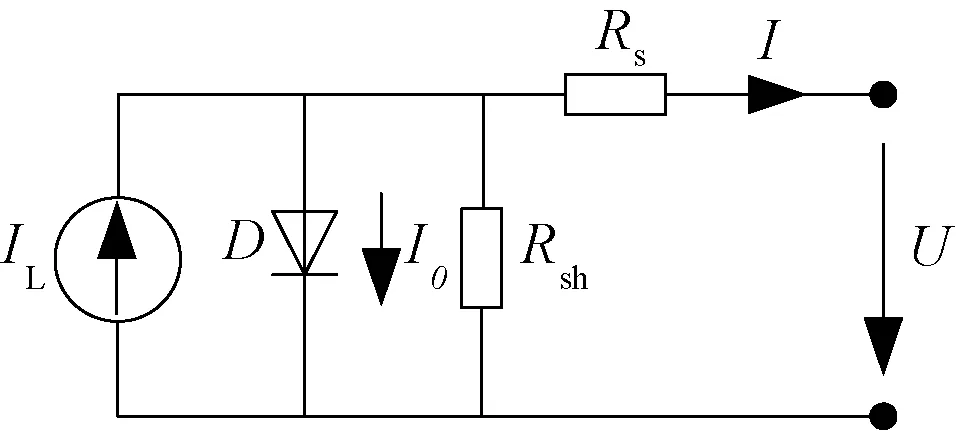
图1 光伏电池等效电路Fig.1 The equivalent circuit of the photovoltaic cell

由上图1，采用KVL可以得到光伏电池物理原理的一般表达为式(1)：

(1)

式中：IL为光电流，A；T为绝对温度，K；I0为反向饱和电流，A；A二极管因子；q为电子电荷，1.6×10-19C；Rs为串联电阻，很小(一般为几Ω)；K为波耳兹曼常数，1.38×10-23C；Rsh为并联电阻，很大(一般为几kΩ)；

由于上述参数大部分都与光照强度和电池温度有关，而光照强度和温度均是随机改变的，所以在一段时间内很难确定这些参数的具体值。因此在工程中一般不采用式(1)进行光伏电池的设计。所以在此问题上，文章采用简单的数学模型得出光伏电池的输出特性，在该模型中只需已知某些很容易测得的参数，就可以建立出精准的数学模型，并且模型应用很广泛，灵活性也很强。

2 光伏电池输出特性模型的建立

2.1 标准测试条件下的U-I特性

则式(1)可以简化为

(2)

(3)

最大功率点时：I=Im，U=Um，开路状态时：I=0，U=Uoc；代入(3)式得

(4)

由(4)式可解得：

(5)

将式(5)代入(2)、(3)式可知只需要利用上述4个基本参变量就可以建立的光伏电池U-I特性方程，并得出U-I输出特性曲线。

2.2 任意温度和光照强度下的U-I、U-P特性

在光伏发电系统的实际应用中，光伏电池的输出特性是随在一天时间里的光照强度和环境温度按照一定规律变化而变化，所以Um、Im、Uoc、Isc也会随之发生改变。通过给定适当的补偿系数以及随机采集某时刻的光照强度和电池温度可以得出以上4个参数随任意光照强度S和电池温度T变化而变化的关系式如下：

(6)

(7)

(8)

(9)

式中：Sref为标准光照强度参考值，Sref=1 000 W/m2；Tref为标准电池温度参考值，Tref=25 ℃；S为实际光强；T为实际温度；ΔS=S-Sref，ΔT=T-Tref；补偿系数a、b、c为固定常数。

采用上述方法得到的工程数学模型并不需要物理模型中复杂的变量参数，只需知道最大功率电压、电流，开路电压、短路电流和任意光照强度、电池温度即可拟合出光伏电池的数学模型，并且可以建模仿真出其U-I、U-P特性曲线。

在 Matlab仿真环境中搭建了光伏电池的工程数学仿真模型如图 2 所示，电池基本参数为：Um=34.8 V，Im=7.47 A，Uoc=44 V，Ise=8.09 A，仿真时补偿系数设置为a=0.002 5 ℃，b=0.000 5 W/m2，c=0.002 88 ℃[9]。其中模块输入变量为温度T光照强度S；通过采集不同时刻的光照强度和温度来分析研究光伏电池的基本输出特性。

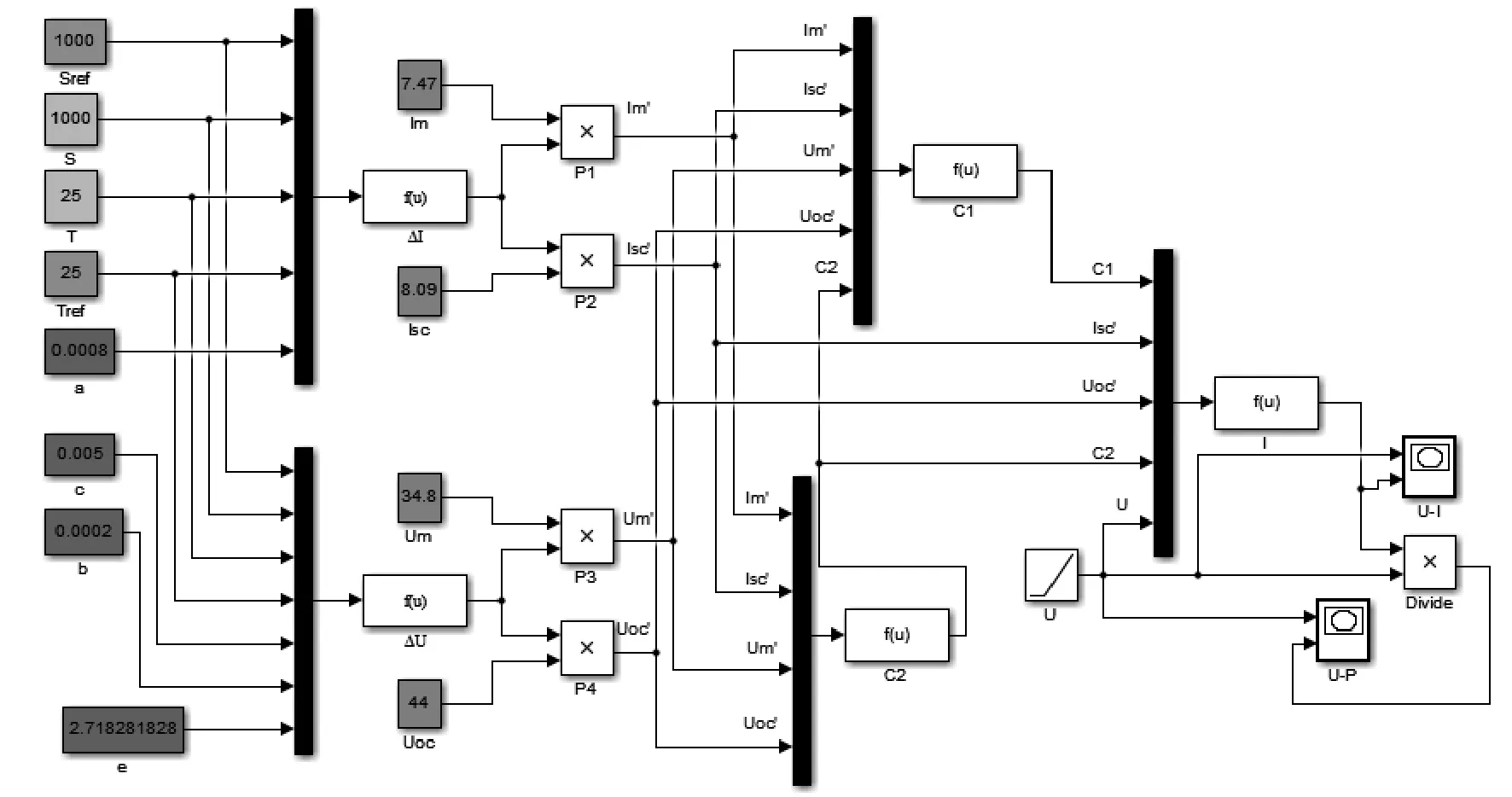
图2 光伏电池的工程数学模型Fig.2 Engineering mathematics model of photovoltaic cells

设定光照强度的额定参考值Sref=1 000 W/m2，温度Tref=25 ℃，并保持恒定不变。改变任意光照强度S和任意电池温度T来分析研究光伏电池的输出特性曲线。

保持温度T为 25 ℃时 , 使得光照强度分别为 600 W/m2、700 W/m2、800 W/m2、900 W/m2、1 000 W/m2时的光伏电池输出U-I、U-P特性曲线分别如下图 3、图 4 所示。

图3 不同光照下的 U-I曲线Fig.3 U-I curves under different illumination

图4 不同光照下的 U-P曲线Fig.4 U-P curves under different light

由图3输出U-I特性曲线可知，当固定电池温度恒等于额定值时，光伏电池输出的电流会随着光照强度慢慢增强而增大。当电压大于45 V时电压基本不随电流改变，可近似为恒压源。当电压小于20 V时电流基本不变化，可近似为恒流源。由图4输出U-P特性曲线可知，当固定电池温度恒等于额定值时，光伏电池的输出功率也会随着光照强度的增强而随之增大。由图4中数条U-P特性曲线可以看出，光伏电池输出最大功率点对应的电压基本固定在一个值，左右偏差很小。这也说明当温度恒定不变时，光照强度的改变对最大功率点对应输出电压影响很小，这也为最大功率点跟踪提供了依据。

保持光照强度S为1 000 W/ m2时，使得温度分别为 15 ℃、25 ℃、35 ℃时的光伏电池输出U-I、U-P特性曲线分别如图 5、图 6 所示。

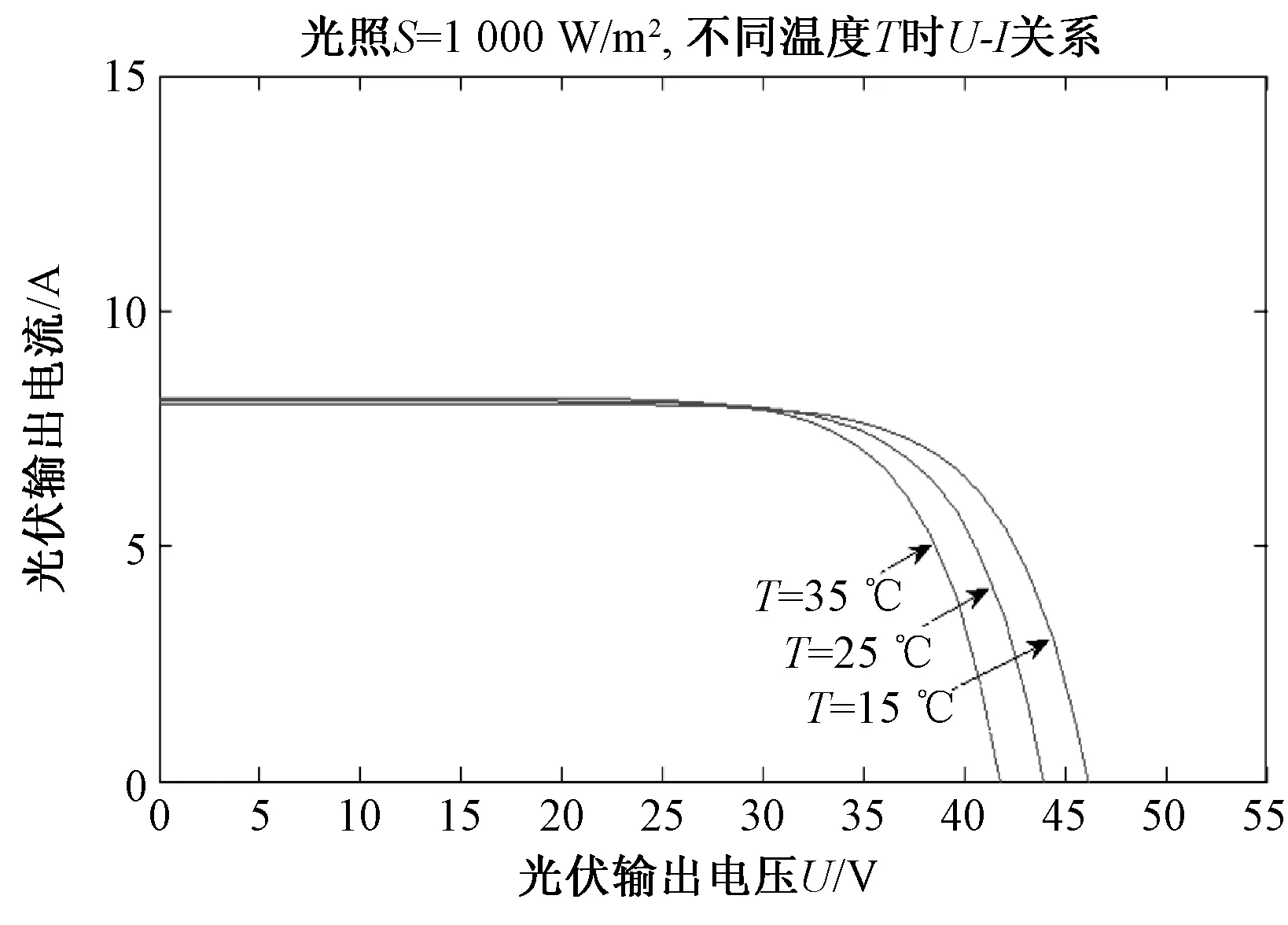
图5 不同温度下的 U-I曲线Fig.5 U-I curves under different temperature

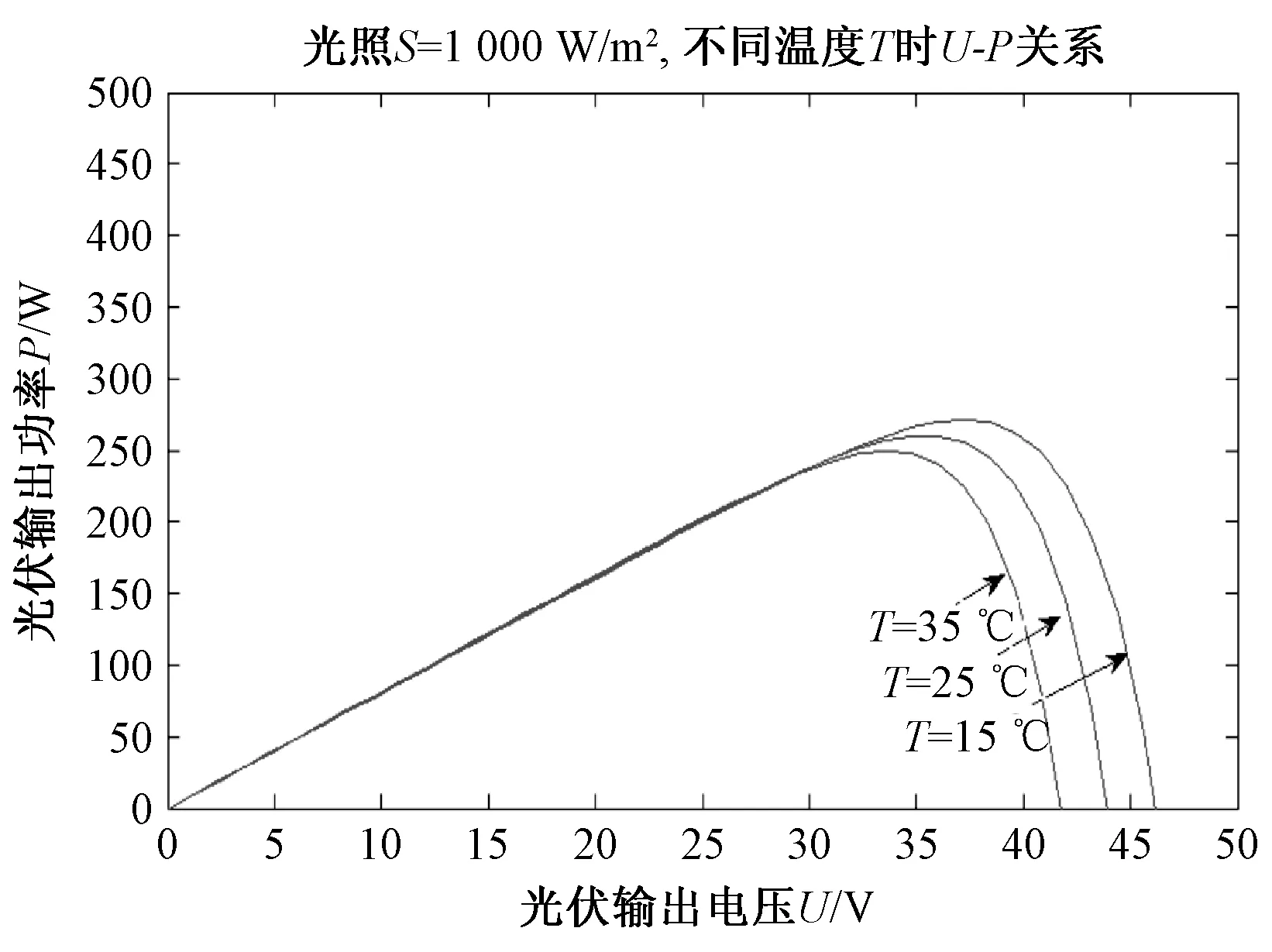
图6 不同温度下的U-P曲线Fig.6 U-P curves under different temperature

由图5所示U-I特性曲线可知，当光照强度恒定不变时，光伏电池输出电压与电池温度成反比关系，而短路电流基本不变，因此最大功率P=UI减小。由图6所示的U-P特性曲线可知，当光照强度恒定不变时，最大功率点对应的电压因温度的改变而有点影响，当电压小于35 V时，光伏电池输出功率与电池温度也成反比关系，温度越高，其输出功率越小，对应输出电压也越小。

光伏电池的U-I、U-P输出特性随温度、光照强度的改变而非线性变化，所以其输出的最大功率点是随时变化的[10]。并且在一天内每个时间点的最大功率点都有差异，每条U-P特性曲线的最大功率点只有一个。

3 最大功率点跟踪(MPPT)

为了能更高效地利用光伏电池所吸收的能量，提高光伏电池对能量的转换效率，就必须时刻都保持在最大功率输出，因此在光伏电池的设计时就必须进行最大功率跟踪[11](MPPT-Maximum Power Point Tracking)，最大功率的跟踪的本质问题实际上就是功率点的自寻优过程[12]。

3.1 改进扰动观察法的最大功率点跟踪

扰动观察法和电导增量法是目前最为常用的跟踪方法，扰动观察法认为负载输出端电压与光伏电池输出功率的变化直接相关[13]，而且然而在实际应用中光照强度和温度是按一定规律改变的，当变化的速度较快时很容易产生误跟踪。而电导增量法则将光伏电池输出的最大功率点对应电压近似认为是负载两端点压，而且其步长为固定的增量，在寻优的过程中需要花费较长的时间，影响光伏电池的工作效率。而光伏系统的最终目的是使得用户最终得到的用电功率最大，也就是负载端功率最大，在输出电流不变的情况下对应着负载端电压也就最大，而负载端电压则有光伏电池输出电压得到[14]。本文利用 Buck-Boost 电路调整负载端输出电压，由跟踪得到的光伏电池输出最大功率点得出对应的光伏电池输出电压Um，然后根据Uo=Um/(1-D)，得出负载输出端电压Uo，也即是负载端最大功率输出时对应的电压。其中D=ton/(ton+toff)=ton/T为占空比。电路原理图如图7所示。

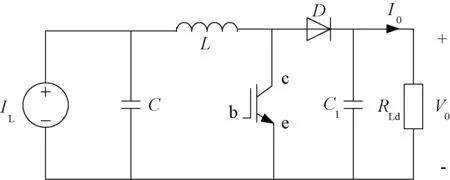
图7 Buck-Boost电路原理图Fig.7 Buck - Boost circuit principle diagram

在不同时刻采用适当调整步长可以更快更稳定的跟踪到光伏电池的输出最大功率点。其中ΔD为占空比D的增量，ΔD1为粗调，设为 0.01，ΔD2为细调，设为 0.001。扰动观察法的MPPT跟踪原理图如图8所示，变步长寻优流程图如图9所示。

图8 MPPT跟踪原理图Fig.8 MPPT tracking principle diagram

图9 变步长寻优流程图Fig.9 Variable step size optimization flow chart

3.2 仿真分析

控制系统计算保持最大功率输出时负载的期望电压，从而求出 Boost 电路进行电压调整达到期望的占空比，再通过锯齿波发生器以及一个比较器生成控制脉冲，从而实现对整个系统的控制。光伏发电系统仿真图如图10所示，图中 MPPT为最大功率点跟踪模块。

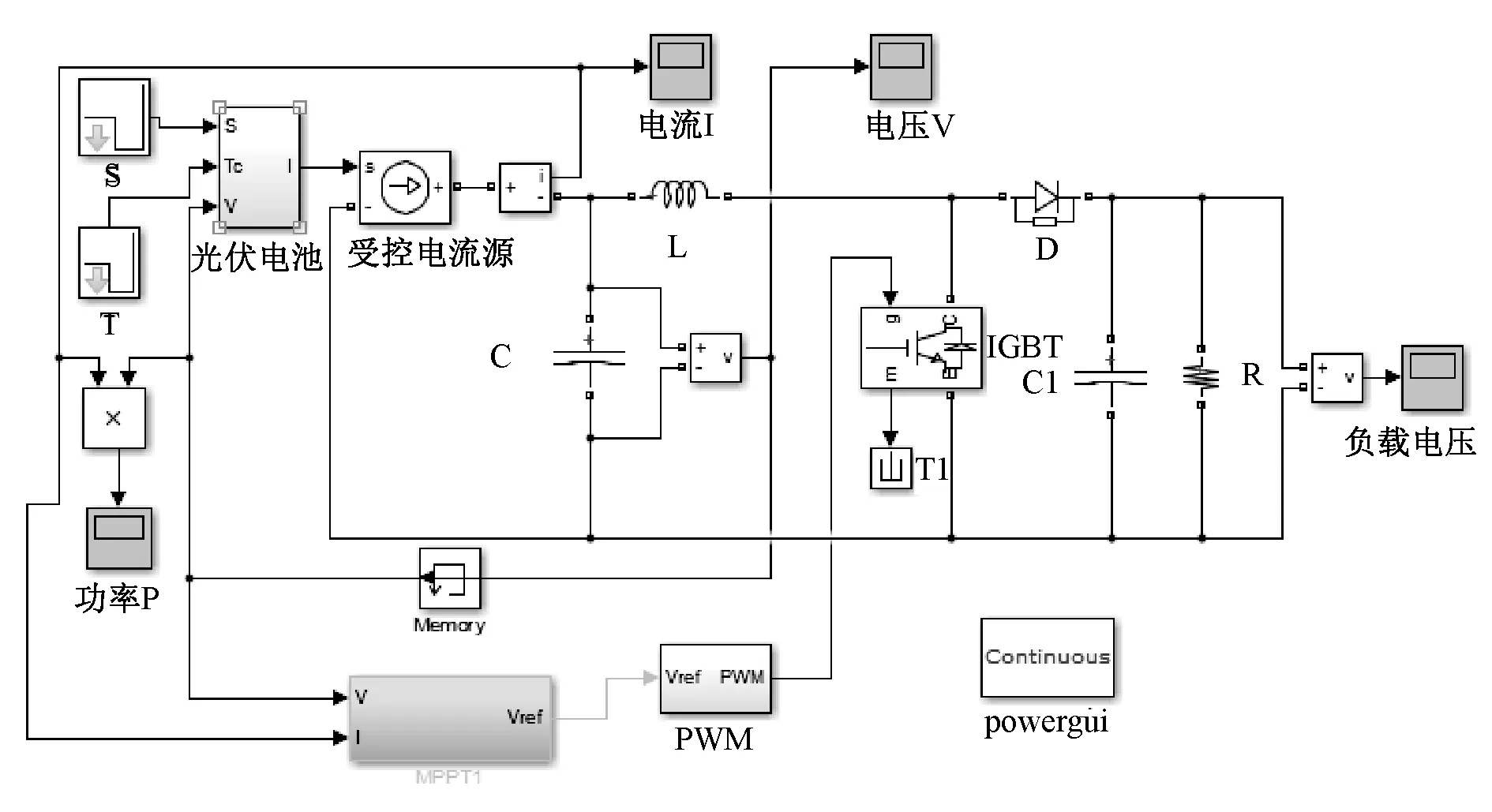
图10 光伏发电工程应用仿真图Fig.10 Photovoltaic engineering simulation diagram

仿真模型中Boost电路参数L=10 mH，C=100 μF，标准参考光照强度Sref=1000 W/m2，环境温度Tref=25 ℃，仿真时为了贴近实际环境变化的真实性，在不同时刻同时改变光照强度和环境温度。为了验证光伏发电系统能否快速地稳定在最大功率点工作状态，分别对光照强度和温度在短时间内改变三次。仿真后得出经过改进扰动观察法控制的各输出最大功率如图11所示。为了体现出改进扰动观察法的优越性，同时还仿真了由电导增量法控制的输出功率，如图12所示。

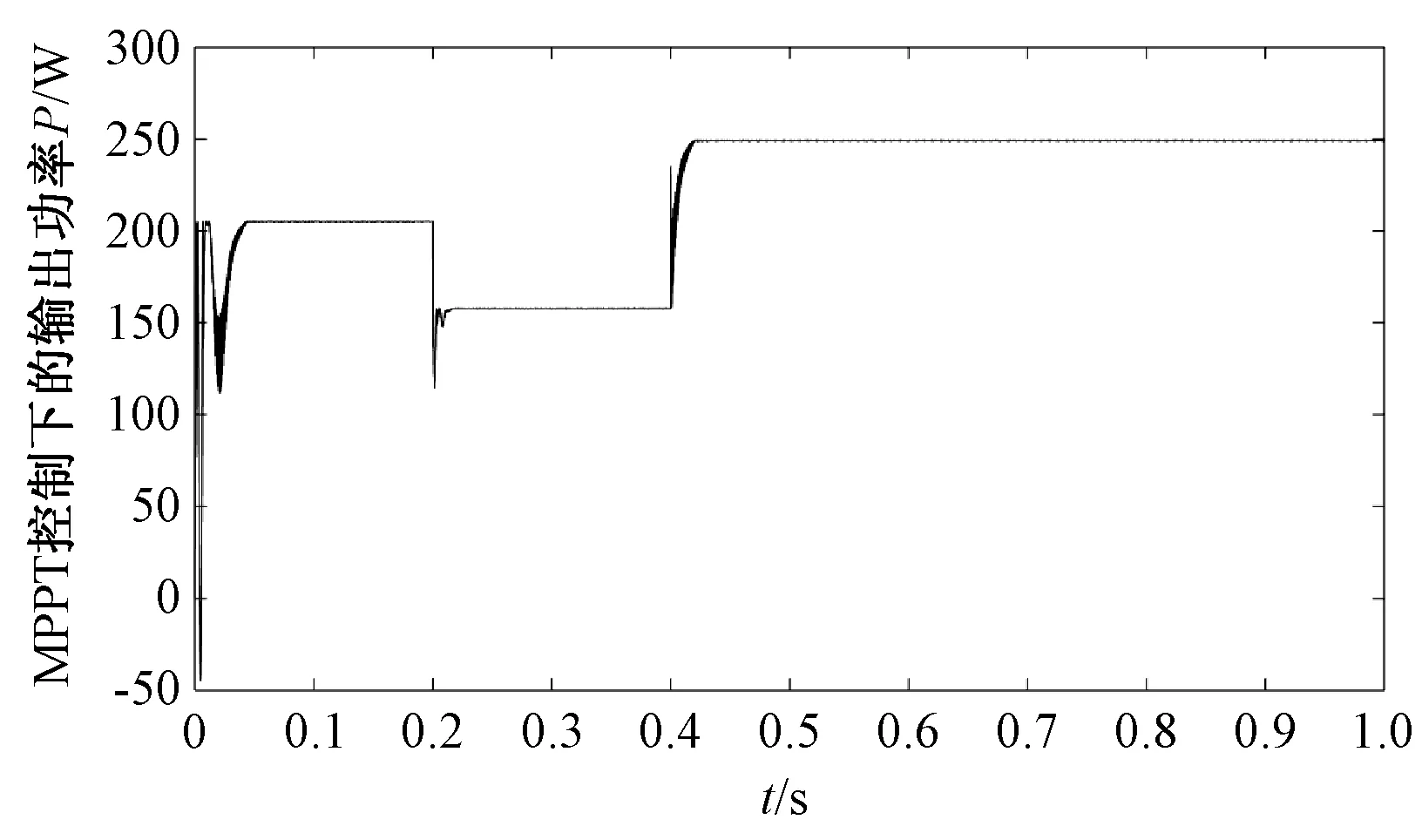
图11 改进扰动观察法控制输出的功率Fig.11 Improve the disturbance observation control output power

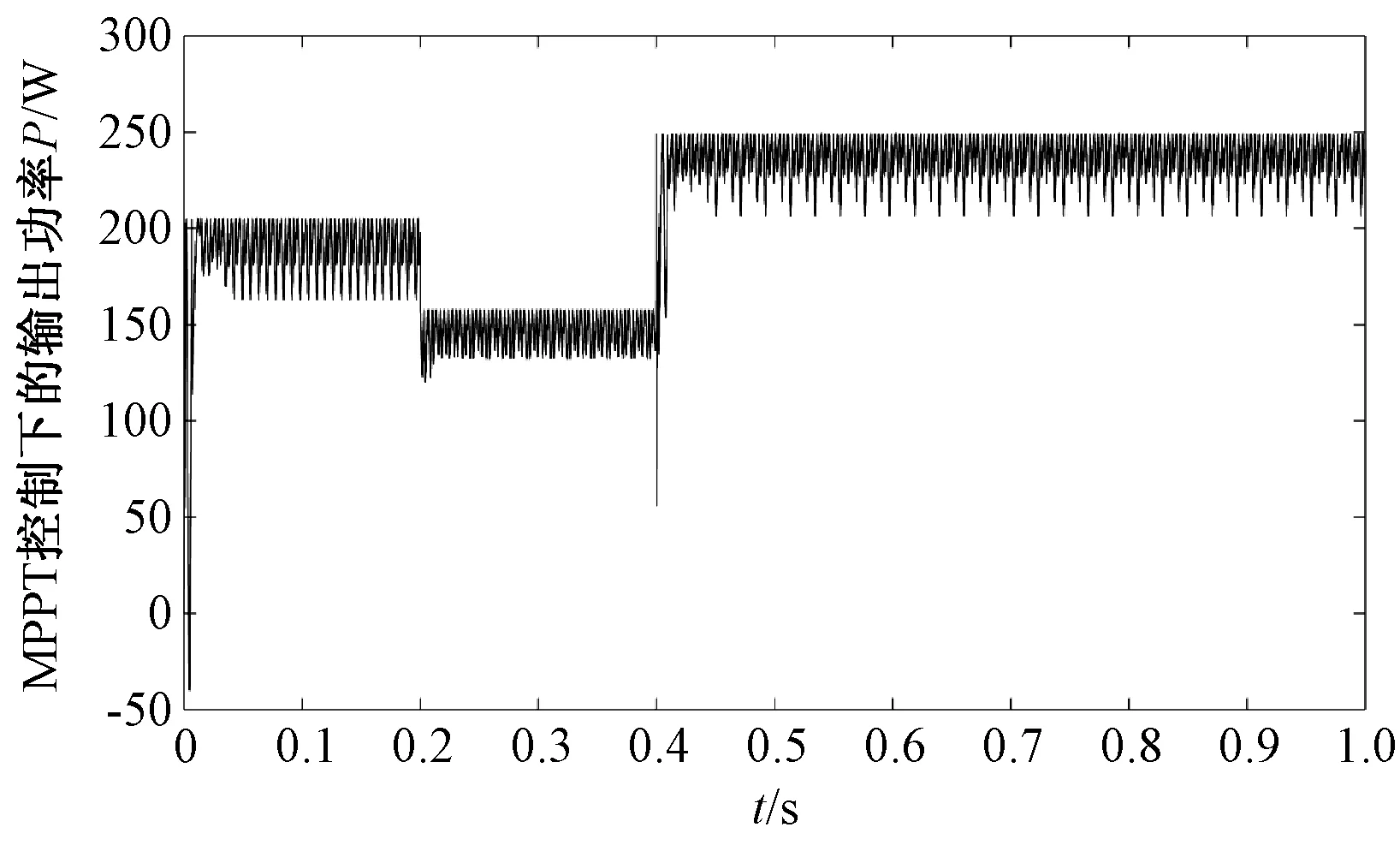
图12 电导增量法控制的输出功率Fig.12 Incremental conductance method to control the output power

由图11可以看出，由于 Boost 电路中含有电容、电感等元件，开始期间需要对其进行充电，因此在运行开始时会产生一些冲击，输出电压不稳定，震荡比较严重，随着光强和温度的稳定使得光伏输出特性各变量趋于稳定运行。初始条件下最大功率输出为210 W，到了0.2 s，虽然温度降低到了15 ℃，但由于光照强度也对应降低到600 W/m2，最大输出功率也随之降到了150 W，并快速地稳定在该值，当运行到0.4 s时，温度升高到35 ℃，但光照强度也升高到1 000 W/m2，最大输出功率也随之升到了250 W，并快速稳定在该最大值运行。

从上述仿真结果可知，虽然由上节U-P特性曲线得出，温度与最大输出功率成反比，但前提是当光照强度恒定不变的情况下才满足。当温度和光照强度同时随时间变化时，其主要影响因素的还是光照强度，光照强度越高输出功率越大，光照强度越低输出功率也就越小。图12为电导增量法控制的输出功率，与图11比可以看出本文提出的改进扰动观察法较电导增量法更快速而精准地将输出功率稳定在一个固定值。

4 结 论

(1) 本文采用工程实用的数学模型来分析研究光伏电池的两个输出特性，通过改变所得数学模型中的一些参变量和固定补偿系数即可得出光伏电池的基本输出特性。

(2) 利用 Matlab 的 Simulink 搭建了光伏电池仿真模型，为了贴合实际光伏电池运行工况，在对应时间内同时改变光照强度和电池温度。光伏电池的U-I、U-P输出特性随温度、光照强度的改变而非线性变化，所以其输出的最大功率点也是随时变化的，并且在一天的任何时间点的最大功率点都有差异，每条U-P特性曲线的最大功率点只有一个。虽然当光照强度稳定时，温度与最大输出功率成反比，但当温度和光照强度同时变化时，起主要影响因数的依然是光照强度，光照强度越高输出功率越大，光照强度越低输出功率也就越小。

(3) 在 Matlab 中建立了具有 MPPT 功能带负载的 Buck-Boost 电路，从仿真结果分析研究可以看出改进扰动观察法比电导增量法更快速而精准地将输出功率稳定在一个固定值，能够很好地进行最大功率点跟踪控制，使得光伏电池工作在最佳状态。此外，模型为光伏和微网系统的进一步研究提供一定的参考。本文不足之处在于仿真时光照强度和温度对应变化，随机性不够高，所以控制算法还有待于提高并加以推广。

[1] 吴海涛，孔娟，夏东伟．基于MATLAB/Simulink的光伏电池建模与仿真[J]．青岛大学学报,2006，21 ( 4): 74-77．

[2] AZZOPARDI B, MUTALE J, KIRSCHEN D, et al. Cost boundaries for future PV solar cell modules sustainable energy technologies [J]. Proceedings of the IEEE Internation Conference on Sustainable Energy Technologies，2008，24 (3): 589-594.

[3] YAZDANI A，DASH P P. A control methodology and characterization of dynamics for a photovoltaic system interfaced with a distribution network[J]. IEEE Transactions on Power Delivery, 2009，24(3):1538-1551.

[4] 田勤曼. 光伏发电系统中最大功率跟踪控制方法的研究 [D]. 天津: 天津大学，2008.

[5] 张忠政，程晓舫. 太阳电池最大功率恒压跟踪研究 [J]．中国电机工程学报，2014，34 (26): 4521-4527.

[6] 张建坡, 张红艳, 马朝晖. 光伏系统变步长最大功率跟踪策略仿真研究 [J]．可再生能源，2009，27 (5): 10-14.

[7] 茆美琴，余世杰，苏建徽. 带有 MPPT 功能的光伏阵列 Matlab 通用仿真模型 [J]. 系统仿真学报， 2005，17 (5): 1248-1251.

[8] 廖志凌，阮新波. 任意光强和温度下的硅太阳电池非线性工程简化数学模型 [J]. 太阳能学报，2009，30 (4): 430-435．

[9] 彭湃，程汉湘，陈杏灿，等.太阳能光伏电池工程用数学模型的研究 [J]. 广东电力，2015，29 (10): 26-29.

[10] 张建成，李倩，周春霞，等. 基于混沌搜索的MAPSO-BPNN在光伏功率预测中的应用研究 [J]. 华北电力大学学报(自然科学版), 2014, 41 (4): 15-21.

[11] 王岩. 光伏发电系统MPPT控制方法的研究 [D]. 北京: 华北电力大学，2007.

[12] 李涛，霍修坤，张道忠，等. 改进扰动观察法的光伏阵列最大功率点跟踪算法 [J]. 微型机与应用， 2013，10(12): 73-76.

[13] 周佳林，郭前岗，周西峰. 光伏系统最大功率跟踪方法的研究及其仿真[J]. 微型机与应用，2011，7(5): 91-93.

[14] 王云亮. 基于DFLC的光伏发电MPPT控制策略的研究 [D]. 天津: 天津理工大学，2011.

Study on Output Characteristic of Photovoltaic Cell and Its Maximum Power Tracking

LI Yong1, CHENG Hanxiang1, CHEN Xingcan2, YU Yin3

(1. Faculty of Automation, Guangdong University of Technology,Guangzhou 510006,China；2. China Mobile Communications Group Guangdong CO., LTD., Guangzhou Branch, Guangzhou 510000,China； 3. Guangdong Power Grid CO., LTD., Dongguan Power Supply Bureau, Dongguan 523008,China)

This paper introduces the practical mathematical model of photovoltaic cell engineering, and analyzes theU-IandU-Poutput characteristic of photovoltaic cells at any temperature and light intensity. Disturbance and observation method is improved and the model of maximum power point tracking (MPPT) is established. By combining with Buck-Boost circuit, control signal can be obtained by PWM thus output voltage of photovoltaic cell will be changed, which makes it possible to achieve the tracking of maximum power point of photovoltaic power generation system. Finally simulation model of photovoltaic cell is established by Matlab and Simulink. The results showed that the higher the temperature is, the smaller the output power will be when the light intensity keeps constant and the output power is proportional to light intensity when the temperature is stable. If the temperature and the light intensity vary at the same time, it is the light intensity that plays a more important role. The improved disturbance and observation method can stabilize the output power at a certain value more quickly and accurately when being compared with incremental conductance method. And the simulation has verified the above conclusion. All of these are of great reference value to the study of photovoltaic system and micro-grid system.

mathematical model; output characteristic; disturbance and observation method; MPPT; Buck-Boost

10.3969/j.ISSN.1007-2691.2017.01.11

2016-05-03.

广东省自然科学基金资助项目(S2011010004950).

TM615

A

1007-2691(2017)01-0070-06

李勇(1991-)，男，硕士研究生，研究方向为电力系统综合自动化；程汉湘(1957-)，男，教授，研究方向为电力系统综合自动化；陈杏灿(1990-)，男，研究方向为电力系统综合自动化；余音(1989-)，女，研究方向为电力系统综合自动化。