一种改进的电力系统静态安全预防控制方法

孙 聪，张 尚，王 涛，顾雪平，仲悟之

(1. 华北电力大学 电气与电子工程学院，河北 保定 071003；2. 中国电力科学研究院，北京 100192)

一种改进的电力系统静态安全预防控制方法

孙 聪1，张 尚1，王 涛1，顾雪平1，仲悟之2

(1. 华北电力大学 电气与电子工程学院，河北 保定 071003；2. 中国电力科学研究院，北京 100192)

针对传统的电力系统静态安全预防控制计算复杂、求解有效性低的问题，提出一种简单、有效的优化求解方法。首先，以机组出力调整量最小为目标，建立预防控制的优化模型；为减小模型规模及计算量，基于主导事件剔除其中的无效约束；为加速搜索最优解，利用基尔霍夫电流定律缩小可行域范围；最后利用基于加权惩罚因子的改进外点法对模型进行求解。IEEE-39节点标准系统及其修改系统算例结果验证了所提方法的有效性。

静态安全；预防控制；主导事件；基尔霍夫定律；外点法

0 引 言

电力系统的静态安全分析仅考虑事故后稳态运行情况安全性，它研究系统中的元件开断引起支路有功潮流及母线电压越限[1]。若有预想事故的发生使得当前运行状态发生线路潮流越限或电压越限，则当前状态处于“正常不安全状态”；否则为“正常安全状态”。对于正常不安全状态，由于系统存在安全隐患，需要对其进行预防控制使之尽量达到“正常安全状态”[2]。因此电力系统静态安全预防控制对于提高电力系统安全水平，确保电力系统安全稳定运行具有重大意义。

电力系统静态安全预防控制方法有很多，大体可分为两类：一是基于灵敏度分析法，二是基于非线性规划方法[3]。灵敏度分析方法简单，无需迭代，调整变量小，便于实施。文献[3,4]提出了一种基于反向等量配对的灵敏度分析方法，该方法同时考虑正、负灵敏度的机组，避免由于机组调整顺序的牵制而一味调整正灵敏度的机组，从而导致平衡机弥补功率缺额而越限。文献[5]提出了一种计及交叉权重的反向等量配对灵敏分析方法，该方法在针对某一越限线路调整机组时，考虑对其它重载线路的调整策略，以避免系统不同线路的反复越限。虽然灵敏度分析方法不断改善，但无法分析多种约束问题，而且对于复杂的电力系统来说也不能完全避免系统的反复越限问题。非线性规划方法，约束考虑全面，调整策略安全性好，但求解复杂。因此很多学者在规划算法上进行了大量研究，文献[6]为加快求解规划速度，提出了一种新型内点算法，该方法给出一种最优中心点搜索模型，从而加快算法收敛速度。为加快收敛速度，提高收敛精度，文献[7]将求解离散变量方便的粒子群算法和优化速度快的内点法结合，解决了非线性规划问题容易陷进死区及内点法难以处理离散问题的缺点。文献[8, 9]为降低求解规模，将灵敏度分析方法用于非线性规划模型中以降低模型变量数目。文献[10]提出基于补偿法建立等效模型，以避免对预想事故态的潮流求解。但对于复杂大型电力系统，补偿法的求解依然计算量很大。文献[11-12]针对静态安全预防控制模型规模大的问题，提出伞约束的概念，认为非伞约束对于规划模型求解是无效的，通过伞约束求解模型来大大减少安全控制模型约束数目，该方法虽然新颖，但筛选伞约束计算太大，得不偿失。

考虑到非线性规划法预防控制的安全性、完整性，本文以非线性规划模型为基础，对该模型的变量约束、线路潮流约束进行改进，并提出了考虑发电机调整量最小的目标函数。由于当前运行状态处于不安全正常状态，而所要寻找的是一个安全正常运行状态，因此采用改进的外点法，从而节约了对初始可行点的寻找时间。所提方法显著地减小了模型规模，简化了求解流程，从而快速、有效地得到发电机组最优控制策略。

1 静态安全预防控制数学模型

1.1 目标函数

由于静态安全预防控制的目的是将不安全正常状态调整到安全正常状态，在这种正常状态下的调整，没有必要切负荷。因此本文只考虑调整机组出力，在考虑一定经济性的基础上，提高系统的安全水平，具体模型如下：

(1)

式中：PG0为当前状态下发电机组出力向量；Pg为待求的正常安全状态运行点。模型是以当前发电机出力PG0与最优发电机出力Pg的向量2-范数作为目标函数，可以尽可能小的减小发电机出力调整，减小调整成本。

1.2 等式约束

本文基于直流潮流模型，只考虑发电机组有功出力调整，等式约束为有功功率平衡约束。模型如下：

(2)

式中：Pgi为发电机i的出力；PDi为节点j的负荷；S和H分别为系统发电机个数、系统总的节点个数。令节点1到S-1为PV节点，节点S为平衡节点，节点S+1到H为PQ节点。

本文提出的基于直流潮流的控制模型在调整中不考虑平衡节点的调整，只要有功功率平衡并且平衡机组出力不越限即可。因此，在求最优运行点时，除平衡机组外的其它发电机组的出力之和可以在一定范围内浮动。有功功率平衡约束可转化为

(3)

式中：Pb，max为平衡节点发电机最大出力限值；PGimax为机组i最大出力限值。

1.3 不等式约束

1.3.1 发电机组出力约束

系统中发电机出力约束如下所示：

(4)

式中：Pg、Pg，min、Pg，max分别为发电机组出力向量、出力向量下限以及出力向量上限。

考虑到机组的出力能力，式(4)中发电机组出力有一个松弛的范围；对于一个发电节点，若考虑基于基尔霍夫电流定律的机组、负荷以及线路分流情况，发电机组的出力范围还可进一步缩小。假设发电节点i接有负荷及线路如下图(1)所示，且线路中线路l1的潮流上限最小。若节点负荷与线路l1的潮流上限之差大于0，如图1(a)，则发电机的最小出力应大于此差值，否则，在线路l2断路时，线路l1将会出现潮流越限。若节点i发电机出力与负荷之差大于0，如图1(b)，则发电机出力应小于节点负荷与线路l1潮流上限之和，否则，在线路l2断路时，线路l1将会出现潮流越限。因此，发电机出力约束可转化为

(5)

式中：PL，max,l为与节点i相连的线路l的传输容量。

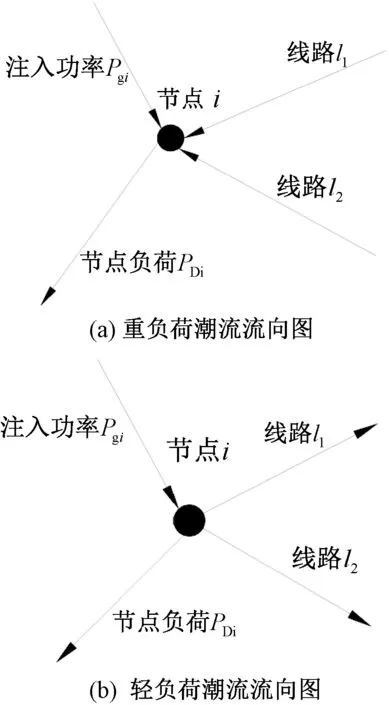
图1 潮流流向图Fig.1 The power flow diagram

1.3.2 线路潮流约束

基于直流潮流模型的线路潮流约束可以表示如下[12]：

(6)

式中：PL，max为支路传输容量向量；G(k)为基态或预想事故状态k下，节点-支路关联矩阵(k=0,1,2,…,m)[13,14]；Gg(k)为G(k)中与发电机对应的列。

由于G只与系统结构参数有关，因此对于系统状态无论是基态还是预想事故态只要改变G就可直接求解相应状态下的潮流，避免了复杂的潮流计算。

1.4 预防控制数学模型

基于上述内容可得电力系统静态安全预防控制模型如下：

(7)

2 预防控制模型的求解方法

2.1 基于主导筛选机制的约束缩减

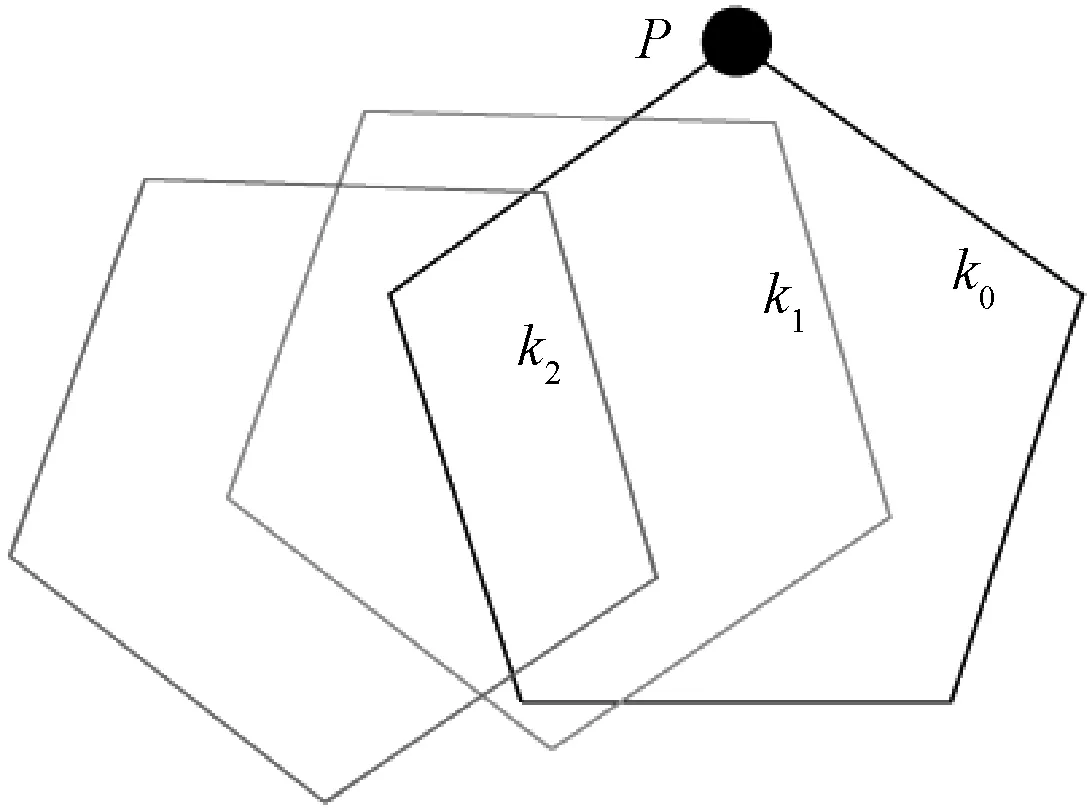
图2 主导事件原理图Fig.2 The principle diagram of dominated events

随着系统规模的增大，控制模型规模也逐渐增大。这主要由于系统线路的增多造成预想事故增多，但实际有些预想事故是不必考虑在内的。因此，本文借鉴主导事件筛选机制[15]，将被主导预想事故删除以缩减支路约束规模。主导事件筛选原理如下：

设在预想事故k下，支路l潮流越限量为

(8)

主导事件筛选理论是指，若预想事故k的每个输电元件越限量都大于预想事故z中相应输电元件的越限量，则预想事故k主导预想事故z，数学模型为

(9)

若两个预想事件对应的所有输电元件越限量相同，则两个事件相互被主导，考虑调整的安全性，将两个预想事故都保留。

基于主导事件筛选预想事故的物理机制可用图2描述，图中k0表示基态下运行模式集合，最优运行运行模式位于顶点P；k1、k2表示预想事故下运行模式集合。若发生预想事故k1、k2，且k2事故的越限量都大于k1事故的越限量，则需要将最优运行点P调至k2运行模式集合区域内以恢复系统安全状态，因此预想事故k1的线路约束无效，则称预想事故k2主导预想事故k1。

2.2 控制模型的求解

对于式(7)，非线性规划模型的求取，若以当前运行点作为初始点寻优则可避免对初始点的求取，但考虑到当前运行点在可行域的外部，因此本文采用外点法求解所提预防控制模型。

2.2.1 传统外点法模型

对于一个一般非线性规划模型：

(10)

可以采用外点法[16]进行求解：

(11)

式中：M为惩罚因子，其收敛标准为‖Xk-Xk-1‖≤e，e为一个极小的正数；R为可行域。

2.2.2 改进外点法模型

传统外点法存在两个缺点：一是无约束极小值模型，没有对控制量加以限制，有可能导致所求发电机出力越限[17]；二是外点法在求解结果时，若要搜索到满足约束的最优解需要迭代很多次，为减少计算量，需要设定一个收敛值e，但这样会使得最终求解结果始终无限接近可行域但不能进入可行域，所求运行点依然为不安全点，如图3所示。针对缺点一，本文通过保留控制量约束，将无约束极小值问题转为约束极小值问题，以避免控制变量越限；针对缺点二，通过微校正线路容量以缩小可行域范围，保证最终所求点为正常安全运行点。如图4所示，在未微校正线路容量时，当前运行点通过外点法求解，最终在原可行域的边界处搜索到最优运行点A，显然此最优点仍然不是安全运行点；通过微校正线路容量后，搜索到最优运行点为B，此时B点已到达安全域成为安全运行点。对于校正系数的确定，可以通过收敛值e确定。

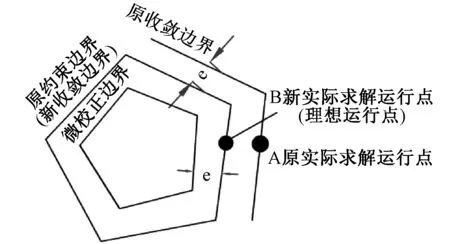
图4 校正可行域示意图Fig.4 The correction feasible region diagram

此外，对线路约束赋予线路重要度权重，可以避免为减小不重要线路越限量而过多调整发电机出力。线路重要度指标为[18]

Mj=Jj×fj

(12)

式中：Jj为线路j介数[19]，fj为线路j电气距离。

综上，基于传统外点法的改进模型如下所示。

(13)

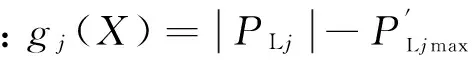
图5 控制模型流程图Fig.5 The procedure flow charts of control model

3 算例分析

本文通过对IEEE 39节点标准系统以及其修改系统进行仿真，验证所提方法的有效性，算例中预想事件仅考虑支路断线故障。本文取初始输入参数e=0.01，M=0.5，c=9。

3.1 IEEE 39节点标准系统

IEEE 39节点系统包括39个节点，46条支路，10台发电机以及21个负荷，系统结构如图6所示。

图6 IEEE 39节点系统结构图Fig.6 The system structure diagram of IEEE-39 bus

(1)线路重要度结果如下表所示

表1为IEEE 39节点系统依据线路重要度指标所求得的46条线路权重。

(2)基于主导事件的预想事故筛选结果

基于主导事件的筛选结果如表2所示，本文考虑N-1线路开断预想事故，筛选前共有46个预想事故，而对于每个预想事故又有46条线路潮流约束，因此筛选前基于预想事故的不等式约束有2 116个。而在筛选后，预想事故缩减为7个，则基于预想事故的不等式约束变为322个，不等式约束减少了1 794个，可见基于主导事件的预想事故筛选模型大大减小了模型规模。

表1 线路重要度算例结果

表2 预想事故筛选结果

(3)模型有效性验证

针对本文所提模型及求解方法，进行优化控制，得到优化前后线路潮流分布如表3所示。

表3 优化前后线路越限情况

从表中可以看出，优化后并不是所有线路都满足N-1扫描，优化率只占76%。这是由于利用本文所提模型仅对越限线路逐一进行优化，结果显示线路13仅通过发电机调整无法满足全部N-1扫描。原因是由于线路13的传输容量为480 MW为其相邻传输线路容量(1 800 MW)的27%，这种悬殊的传输容量是导致无解的根本原因。

为证明本文在优化调度时，考虑线路重要度的优越性，下面求解不考虑线路重要度的预防控制模型。优化后两种情况的线路越限水平相当，但发电调度优化结果相差悬殊，如表4所示。从表中可以看出考虑线路重要度的预防控制模型发电调度量更小些，因为此种控制策略考虑局部重要线路最优，而非盲目寻全局最优解。以发电机35为例，其最大发电机出力为687 MW，但线路36(22-23)的传输容量为600 MW，若不考虑线路重要度优化，35机组(G5)出力498.052 0 MW，调整量为151.948 0 MW；但若考虑线路重要度优化，35机组出力687 MW，调整量为37 MW，虽然此种优化会导致线路36越限，但从表1中可以看出，线路36的重要度仅为0.005 4，远远落后于其它重要线路，显示了所提模型的优越性。

表4 考虑线路重要度的优化前后线路越限情况

(4)精度校验

本文考虑到静态安全预防控制的时效要求，基于直流潮流建立控制模型，但在实际电网基于交流潮流运行，因此需要对优化后的发电机出力用于交流系统中进行潮流校验，校验结果如表5所示，从表5中可以看出直流校验结果与交流校验结果大体近似，因此，直流校验结果满足交流系统正常安全运行要求。

表5 优化结果交直流校验

3.2 IEEE 39节点修改系统

从对IEEE 39 节点标准系统进行控制，结果测得3、13、38线路仅依靠发电机调度无法避免N-1扫描越限。因此，本文将以上三条线路分别提高线路容量50%、30%、40%，使得存在可行域。对修改后IEEE 39节点系统，利用所提模型进行控制，得到预想事故筛选结果如表6所示，发电机优化结果如表7所示。

表6 预想事故筛选结果

从表6可以看出，提高线路3、13、38的容量后，预想事故缩减为6个，则基于预想事故的不等式约束变为276个，不等式约束减少了1 840个，可见提高线路容量，进一步减小了模型规模。

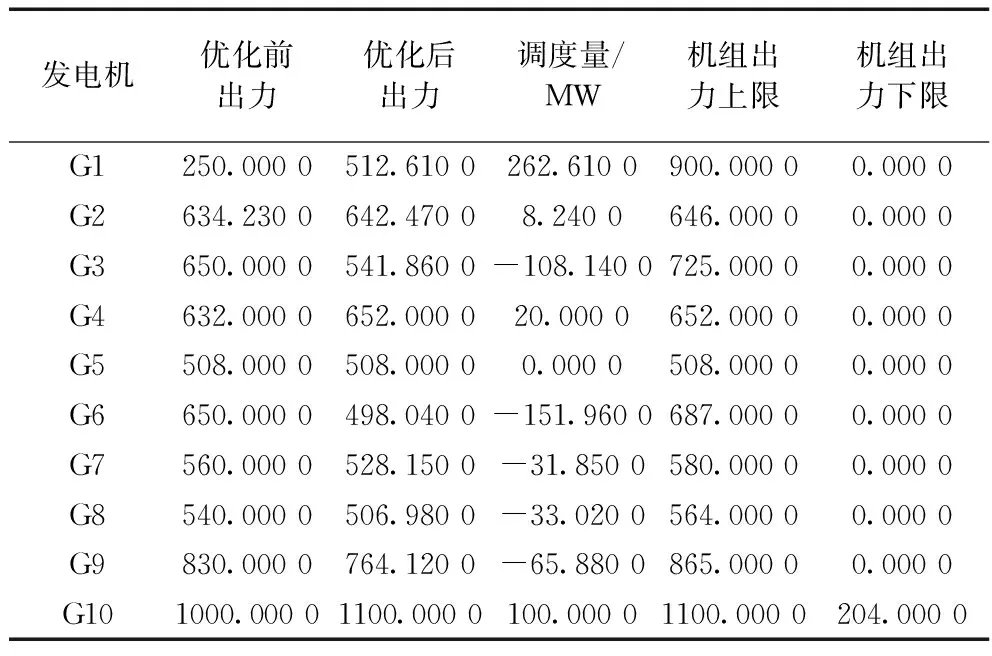
表7 优化前后发电机出力对比表对比

从表7可以看出，发电机优化前后出力在合理范围内且满足功率平衡，因此，优化合理。同时，采用交流潮流校验优化前后线路潮流越限情况，从表8中可以看出，系统运行状态可以调整到安全运行状态。

表8 优化前后线路潮流越限量对比

4 结 论

本文提出了一种简单有效的电力系统静态安全预防控制方法。基于直流潮流支路约束等效模型，建立静态安全预防控制模型；根据基尔霍夫电流定律，缩小发电机出力可行域范围以加速搜索最优解；采用改进外点法进行求解以避免搜索初始点而降低求解效率；考虑线路重要度及发电调整量，对不存在正常安全可行域的系统，优先考虑重要越限线路的调整以避免发电机盲目调整。对IEEE 39节点系统进行仿真校验，通过对比优化前后线路越限量，验证了所提方法的有效性；对于不存在可行域的情况，通过对比两种优化策略的发电力出力变化，验证了所提方法的优越性。

[1] 丁平，李亚楼，徐得超，等．电力系统快速静态安全分析的改进算法[J]．中国电机工程学报，2010，30(31)：77-82．

[2] 吴际舜．电力系统静态安全分析[M]．上海：上海交大出版社，1985．

[3] 李海涛，孙闻，赵兵，等．基于交流灵敏度的在线安全控制策略[J]．电力系统及其自动化学报，2012，1(24)：32-36．

[4] 程临燕，张保会，郝治国，等．基于综合灵敏度分析的快速控制算法研究[J]．电力自动化设备，2009，4(29)：46-49．

[5] 刘文颖，徐鹏，梁才，等．一种计及交叉权重的有功校正控制算法[J]．电工技术学报，2014，29(8)：281-288．

[6] 杨林峰，简金宝，韩道兰，等．基于最优中心参数的多中心校正内点最优潮流算法[J]．中国电机工程学报，2012，32(4)：136-144．

[7] 吴小珊，张步涵，袁小明，等．求解含风电场的电力系统机组组合问题的改进量子离散粒子群优化方法[J]．中国电机工程学报，2013，33(4)：45-52．

[8] 刘水平，刘明波，谢敏．基于轨迹灵敏度的电力系统模型预测切负荷控制方法[J]．中国电机工程学报，2010，30(34)：28-35．

[9] 孙景强，房大中，锺德成，等．暂态稳定约束下的最优潮流[J]．中国电机工程学报，2005，12(25)：12-17．

[10] 阳育德，冯彦维，韦化．基于补偿法的预防性静态安全控制[J]．电力自动化设备，2015，35(12)：47-54．

[11] ARDAKANI A, BOUFFARD F．Identification of umbrella constraints in dc-based security-constrained optimal power flow[J]．IEEE Transactions Power Syst，2013，28(4)：3924-3934．

[12] ARDAKANI A, BOUFFARD F．Acceleration of umbrella discovery in general scheduling problems[J]．IEEE Transactions Power Syst，2015，30(4)：3924-3934.

[13] 陈思捷，陈启鑫，夏清．静态安全距离：概念，模型和意义[J]．中国电机工程学报，2015，35(3)：600-608．

[14] CHEN S J，CHEN Q X，XIA Q，et al．Steady-state security assessment method based on distance to security region boundaries[J]．IET Generation， Transmission & Distribution，2013，3(7)：288-297．

[15] CAPITANESCU F，GLAVIC M，ERNST D，et al．Contingency filtering techniques for preventive security-constrained optima power flow[J]．IEEE Transactions on Power Systems，2007，4(22)：1690-1697．

[16] 黄文涛，邓长虹，汪志强，等．基于外点罚函数法的实时低频切泵策略[J]．中国电机工程学报，2013，16(33)：104-111．[17] VERONICA B，IGOR G，BYONG K．Exterior-point method for support vector machines[J]．IEEE Transactions on Neural Networks and Learning Systems，2014，25(7)：1390-1393．

[18] 胡健，杨宣访，周清锋，等．基于无功-相角静态安全域的预想事故自动选择[J]．华北电力大学学报(自然科学版)，2014，41(5)：31-34．

[19] 严弈遥，罗禹贡，朱陶，等．融合电网和交通网信息的电动车辆最优充电路径推荐策略[J]．中国电机工程学报，2015，35(2)：310-318．

An Improved Method of Static Security Preventive Control in Power Systems

SUN Cong1, ZHANG Shang1, WANG Tao1, GU Xueping1, ZHONG Wuzhi2

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China; 2. China Electric Power Research Institute, Beijing 100192, China)

This paper proposes a simple and effective optimal solution method to deal with problems such as complex calculation and low efficiency of the solution of static security preventive control in power system. First of all, the optimal model of preventive control is established. The objective function is the minimum adjustment of the output of generating units. In order to reduce the model size and the amount of calculation, the dominant events method is employed to eliminate invalid constraints. In addition, by using the Kirchhoff’s current law, the feasible region scope is narrowed to accelerate the search of optimal solution. Finally, the improved external point method based on weighted penalty factor is adopted to solve the proposed model. Simulations are made on IEEE-39 bus system and its modified version. The results show that the proposed method is effective for static security preventive control.

static security; preventive control; dominant events; the Kirchhoff’s current law; external point method

10.3969/j.ISSN.1007-2691.2017.01.04

2016-05-03.

国家自然科学基金资助项目(51277076)；中央高校基本科研业务费专项资金资助项目(2015XS109).

TM711

A

1007-2691(2017)01-0024-07

孙 聪(1992-)，女，硕士研究生，研究方向为电力系统安全防御与恢复控制；张尚(1991-)，女，博士研究生，研究方向为电力系统安全防御与恢复控制；王 涛(1976-)，男，副教授，研究方向为电力系统安全防御与恢复控制、复杂网络理论及其应用；顾雪平(1964-)，男，教授，博士生导师，研究方向为电力系统安全防御与恢复控制、电力系统安全稳定评估与控制、智能技术在电力系统中的应用；仲悟之(1979-)，男，高级工程师，研究方向为电力系统仿真与分析研究。