非理想条件下分布式MIMO雷达目标检测
2017-03-16陈明建龙国庆黄中瑞
陈明建,龙国庆,黄中瑞
(合肥电子工程学院,合肥 230037)
【信息科学与控制工程】
非理想条件下分布式MIMO雷达目标检测
陈明建,龙国庆,黄中瑞
(合肥电子工程学院,合肥 230037)
针对任意波形相关、任意阵列配置情况下分布式MIMO雷达目标检测问题,提出了一种基于Cholesky分解的MIMO雷达检测器;首先分析了分布式MIMO雷达回波的相关性,并给出了任意阵列配置时MIMO雷达检测算法;同时,为了解决发射波形相关矩阵出现奇异性导致无法获得检测统计量的问题,提出了基于Cholesky分解的分布式MIMO雷达检测方法,给出了统一框架下的检测统计量表达式,推导了虚警概率和检测概率的近似解析式;研究得出:在低信噪比情况下,相关性越大,检测性能越好;在高信噪比时,相关性越小,检测性能越优;最后数值仿真验证了理论分析的有效性和正确性。
分布式MIMO雷达;相关波形;目标散射系数;检测统计量;似然比检测
多输入多输出(MIMO)通信系统利用各种分集技术,如空间分集、波形分集、极化分集以及频率分集等显著地降低了信道衰落对信噪比的影响,提高了信道容量。受此启发,人们将MIMO的概念拓展到雷达领域,相继提出了MIMO雷达的概念[1-4]。MIMO雷达是利用多个发射天线同步地发射分集的波形,同时使用多个接收天线接收回波信号,并集中处理接收信号的一种新型雷达。根据天线配置的远近,MIMO雷达主要分为两种类型:集中式MIMO雷达[5-6]和分布式MIMO雷达[7-8]。集中式MIMO雷达是在传统相控阵雷达的基础上引入了发射波形分集的思想,通过形成虚拟孔径提高雷达性能[9-10]。分布式MIMO雷达收发阵元间距足够大,以此获得空间分集提高雷达性能。与集中式MIMO雷达相比,分布式MIMO雷达更加充分体现了分集的思想,通过分集增益提高雷达系统目标检测性能和参数估计能力[11-13]。
目标检测是分布式MIMO雷达研究的一个重要方面[14-15],在理想情况下通过发射多个正交波形和收发阵元大间距配置获得空间分集增益,从而提高分布式MIMO雷达检测性能。文献[7]研究了施威林目标模型下分布式MIMO雷达的检测问题,在Neyman-Pearson准则下,推导了各种不同空间配置下分布式MIMO雷达的最优检测器。与传统相控阵雷达相比,在高信噪比条件下具有更优的检测性能。但文中假定要求收发阵元具有很大的间距,不同分集通道目标散射系数彼此相互独立。然而在实际应用中MIMO空间配置并不完全满足要求,同时发射波形也可能部分相关[16],即使MIMO雷达发射的是具有低旁瓣的正交波形集,由于目标引起的时延、多普勒频率也会影响接收端回波的正交性。针对这个问题,文献[17]研究了相关路径下MIMO雷达检测性能,利用特征函数与概率密度函数的关系,推导了一般MIMO模型的检测统计量,得到了恒虚警时检测概率的解析式。文献[18-19]研究了分集路径不完全独立时基于似然比检测的MIMO雷达检测方法,分析了分集路径相关性对检测性能的影响,但未考虑波形相关对MIMO雷达检测性能的影响。文献[20]研究了发射非正交波形时MIMO雷达的分集增益不大于散射点数目和收发天线数目的最小值,给出了检测统计量表达式。文献[21]研究了各类施威林目标任意波形时的MIMO雷达检测性能,假设分集路线完全独立,没有考虑分集路径相关对检测性能影响。
针对上述问题,本文研究任意波形相关和任意阵列配置情况下MIMO雷达目标检测方法。首先给出了一般分布式MIMO雷达信号模型,分析发射正交波形、任意阵列配置时MIMO 雷达检测方法;接着,分析了发射任意相关波形MIMO 雷达检测方法,提出了利用Cholesky分解方法解决了二元假设中数据协方差病态问题,得到了检测统计量,推导了检测概率与虚警概率的近似解析表达式。最后数值仿真验证了理论分析的有效性和正确性。
1 MIMO雷达信号模型
考虑远场扩展目标和分布式MIMO雷达配置如图1所示,忽略目标和雷达阵元的高度。

图1 分布式MIMO雷达空间配置示意图

为简化分析,不考虑目标的运动速度,则第n个阵元接收目标回波信号为M个发射信号的线性叠加,可表示为
(1)
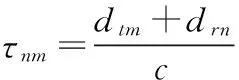
假设MIMO中各接收通道与发射信号匹配滤波后的输出为

(2)
其中

(3)
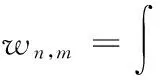
(4)
wn,m经过匹配滤波后的通道噪声,其均值为零,且协方差满足



(5)
若将所有接收阵元的匹配输出矢量写成向量形式为
(6)


2 回波的相关性分析
由于收发阵元采取大间距配置和发射波形分集,分布式MIMO雷达目标表现为空间散射多样性和发射波形多样性,从而目标回波序列之间的相关性分为空间相关性和波形相关性。空间相关性反映了对于不同收发阵元的散射系数的关系;波形的相关性反映了对于不同发射阵元的相关性以及同一发射阵元信号的自相关和互相关特性。
3.1 散射系数的相关性
由文献[7]可知,任意通道的散射系数可表示为
(8)
其中∑(x,y)位于矩形内点(x0+x,y0+y)上的散射体的复散射增益,散射系数αn,m的协方差为
(9)
其中
(10)
利用积分等式:
(11)
其中sinc(x)表示归一化的辛克函数。根据式(11)则式(9)可简化为
(12)
为了考察任意两个分集路径之间的相关性,定义分集路径散射系数αn,m、αn′,m′之间相关系数为
(13)

(14)
由式(10和式(14)可知散射系数相关性与MIMO雷达天线配置、目标位置、目标尺寸及载波频率均有关。由于ρ(n,m,n′,m′)为二维sinc函数,因此可以根据sinc函数的特点分析散射系数的相关性,下面分3种情况讨论其相关性。



3.2 发射信号的相关性
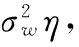
2) 假定分布式MIMO满足空间分集要求,即散射系数完全独立Rc=IMN,当发射波形为非正交波形时,此时匹配滤波器输出后的目标回波α′=ηα,满足α′~CN(0,ηηH),等效分布式MIMO雷达阵元配置不满足空间分集要求,减少了独立的通道数,降低了空间分集效果。
4 分布式MIMO雷达检测器
理想情况下分布式MIMO雷达收发阵元采取大间隔配置,利用空间分集和波形分集提高雷达性能。然而在实际工程应用中,MIMO雷达的阵元配置可能并不完全满足空间分集要求,此时目标散射系数并非完全独立,存在部分相关性,同时发射波形也并非完全正交,即使MIMO雷达发射的是具有低旁瓣的正交波形集,由于目标引起的时延、多普勒频率也会影响接收端回波的正交性。下面具体分析任意阵元配置和任意波形相关时MIMO目标检测方法。
4.1 任意阵元配置时MIMO目标检测
当分布式MIMO雷达收发阵元间距任意配置时,阵元间距可能不满足空间分集要求,此时分集通道不再是相互独立的,而是存在部分相关性。为了讨论非理想情况下MIMO雷达检测性能,首先考虑发射波形相互正交、分集通道存在部分相关时MIMO检测器设计。然后再分析任意发射波形、任意阵元配置时MIMO雷达检测方法。
假定H0表示目标不存在,H1表示目标存在。根据以上分析,x可表示为
(15)
在H0或H1假设条件下回波信号的协方差矩阵分别为
(16)

i=0,1
(17)
假设已知目标和噪声电平,根据Neyman-Pearson 准则,在给定虚警概率的条件下,最优检测器可以通过似然比得到,即
(18)
由于似然比中的常数最终可以并入检测门限中,因此可以舍弃无关常数项k0,可得如下检测统计量
(19)
根据矩阵求逆引理可得
(20)

(21)


(22)
此时,检测统计量变为
(23)
命题1:若矩阵A为半正定矩阵,则BABH为半正定矩阵。
证明:由矩阵理论可知,A为半正定矩阵的充要条件是存在矩阵C,满足A=CCH。因此BABH=BCCHBH=BC(BC)H,因此BABH为半正定矩阵。证毕。
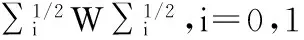
(24)


(25)

(26)

根据命题2,任意阵列配置时分布式MIMO雷达虚警概率和检测概率分别为
(27)
其中QΓ(γ,Λ0)、QΓ(γ,Λ1)分别表示在两种假设条件下不完全伽马分布的累积分布函数。
为简化研究问题,定义MIMO雷达分集路径相关系数为
(28)

4.2 任意波形相关时MIMO目标检测
假定矩阵η的秩为K,1≤K≤MN,对矩阵η进行Cholesky分解可得η=AAH,其中A∈CMN×K为列满秩矩阵。同理可得Rα=BBH
定义x=Ax1,其中x1为K×1维复高斯随机矢量,均值为零,协方差矩阵为
(29)
(30)
其中ξ=E/M。
根据矩阵求逆引理公式(A+BCD)-1=A-1-A-1B(DA-1B+C-1)-1DA-1,可得
(ξAHRαA+IK)-1=IK-AHB(SNRBHAAHB+I)-1BHA
(31)
将式(31)代入式(30),并化简可得检测统计量为
T(x)=x1AHB(ξBHAAHB+I)-1BHAx1=
xHB(ξBHAAHB+I)-1BHx
(32)
利用矩阵等式变换
B(I+AB)-1=(I+BA)-1B
(33)
根据式(32)、式(33)可得
T(x)=xH(ξBBHAAH+I)-1BBHx=
xH(ξRαη+I)-1Rαx=xHUx
(33)
其中U=(ξRαη+I)-1Rα。
接下来讨论几种特殊情况时,任意配置、任意波形时分布式MIMO雷达目标检测的充分统计量情况:
1) 若发射波形集相互正交,即η=IMN,U=W,此时式(21)、(34)等价;
2) 若发射波形集相关,MIMO雷达阵元配置完全满足空间分集要求,即η≠IMN、Rα=IMN,此时式(34)可简化为T(x)=xH(ξη+I)-1x;
3) 若发射波形集相互正交,且MIMO雷达阵元配置完全满足空间分集要求,即η=IMN、Rα=IMN,此时式(21)、(34)均可简化为T(x)=‖x‖2,该检测统计量与文献[2]结果相吻合。
由于匹配接收矢量x服从零均值复高斯分布,而任意波形相关、任意阵列配置时分布式MIMO雷达的检测统计量可简化为式(34),即检测统计量为加权的卡方分布,因此可利用命题2的结论,可近似求解检测概率和虚警概率的解析式。
4 仿真实验与结果分析
在理论分析的基础上,本节通过计算机数值仿真考察验证分集路径存在相关时,分布式MIMO雷达检测性能。仿真条件:M=2,N=4,为简化分析,假定所有分集路径的路径损耗均相等,虚警概率Pfa=10-8。
仿真1:不同阵元间距和分集路径相关时的检测性能
图2表示不同阵元间距时MIMO雷达检测性能;图3表示不同相关系数时MIMO雷达检测性能。
由于不同阵元间距会影响MIMO雷达的分集路径的相关性,图2给出了不同阵元间距时分布式MIMO雷达检测概率随信噪比的变化曲线。图2中共考察6种不同情况下检测器的性能。其中4种情况分别是阵元间距为50λ、100λ、150λ、200λ,另外两种情况是理想的分布式MIMO雷达(分集路径是不相关的或独立)和传统相控阵雷达(分集路径是全相关)。

图2 不同阵元间距时检测概率与信噪比关系曲线
由图2可知:由于阵元间距不同,分布式MIMO雷达的分集路径相关性存在差别,间距越大,相关程度越小;在低SNR情况下,分集路径的相关度越大,检测性能越好;而在高SNR情况下,分集路径的相关度越小,检测性能越好;在一定的检测概率情况下,如Pd≥0.8时,理想分布式MIMO 雷达要优于相关分集路径情况下的检测性能,这也是分布式MIMO雷达相比传统雷达性能更加优越的关键所在。
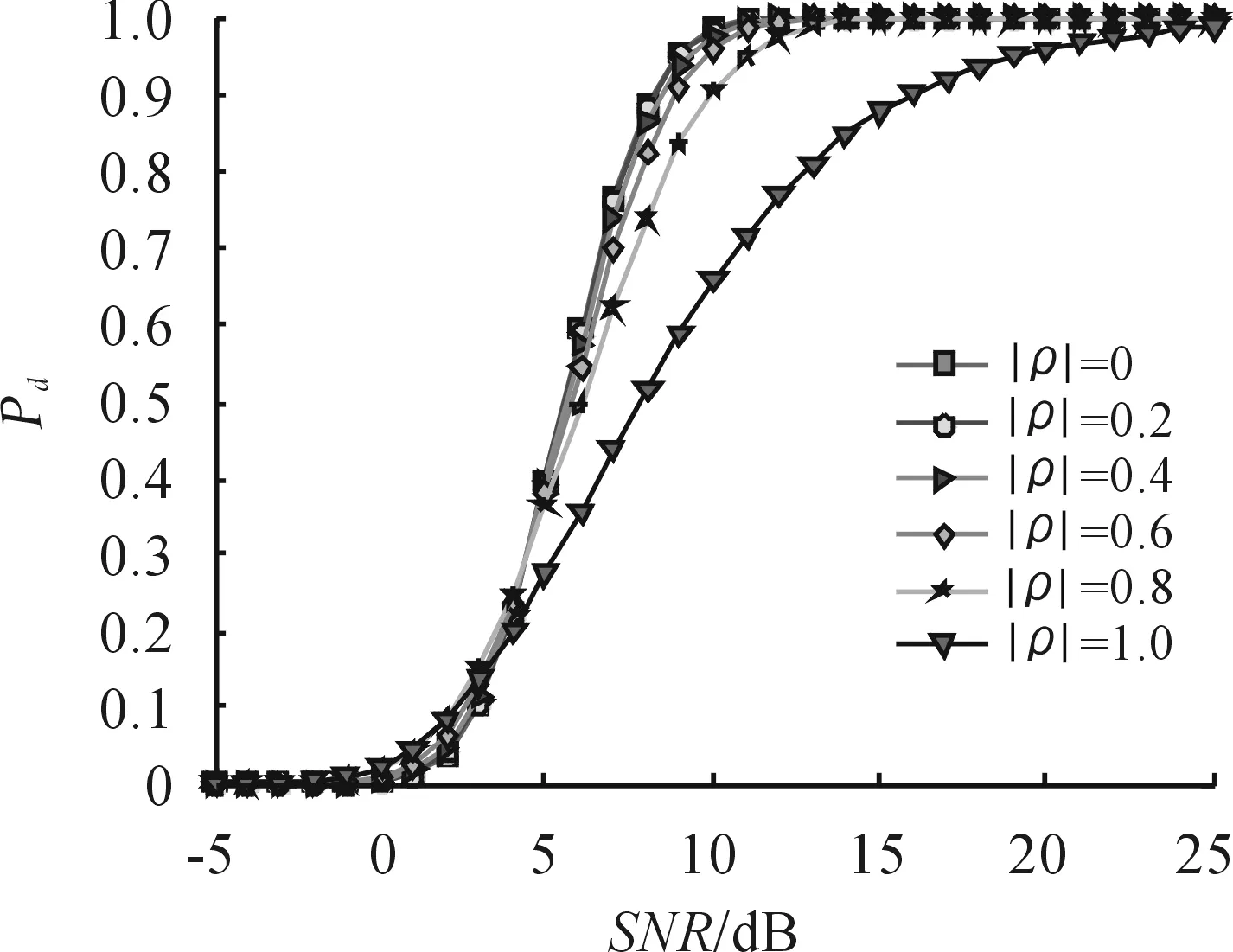
图3 不同相关性时检测概率与信噪比关系曲线

仿真2:任意波形相关时检测性能

考虑波形的峰值旁瓣比一定程度上反映了波形的相关性,且发射波形的正交性和分布式阵元布置共同保证了独立的分集路径,因此波形的相关性不仅会影响相干处理增益,还会影响MIMO雷达空间分集增益。

图4 任意波形相关时MIMO雷达检测概率与信噪比关系曲线

图5 分集路径与波形均相关时MIMO雷达检测概率与SNR关系曲线
由图4、图5可知:在低SNR情况下,发射波形集相关性越大,检测性能越好;而在高SNR情况下,波形集相关性越小,检测性能越好。结论是:在低信噪比条件下,相干处理增益占优,而在高信噪比条件下空间分集占优。
5 结论
1) 本文研究了非理想情况下分布式MIMO雷达检测方法和性能,推导了任意波形相关和任意阵列配置时检测器的充分统计量服从加权卡方分布,得到了检测概率与虚警概率的近似解析表达式。
2) 波形和分集路径相关性均会降低分布式MIMO的空间分集能力,在低信噪比时,这种相关性能够改善空间分集MIMO雷达的检测性能,而在高信噪比时,相关性使得空间分集MIMO雷达的检测性能下降。相关性越强,检测性能越差。
[1] FISHER E,HAIMOVICH A M,BLUM R S,et al.MIMO Radar:an Idea Whose Time Has Come[C]//Radar Conference,2004.Proceddings of the IEEE,2004:71-78.
[2] FISHER E,HAIMOVICH A M,BLUM RS,et al.Performance of MIMO Radar Systems:Advantages of Angular Diversity[C]//Proceeding of.38th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA USA,November,2004:305-309.
[3] BLISS D.W.and FORSYTHE K.W.Multiple-Input Multiple-Output(MIMO) Radar and Imaging:Degrees of Freedom and Resolution[C]//Proceeding 37th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA USA,November,2003:54-59.
[4] FORSYTHE K,BLISS D,and FAWCETT G.Multiple-Input Multiple-Output(MIMO) Radar:Performance Issues[C]//proceeding of.38th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA USA,November,2004:310-315.
[5] LI J,STOICA P.MIMO Radar with Colocated Antennas[J].IEEE Signal Processing,2007,24(5):106-114.
[6] LI J,STOICA P.MIMO Radar Signal Processing[M].New York:Wiley,2008.
[7] FISHLER E,HAIMOVICH A M,BLUM R S,et al.Spatial Diversity in Radars - Models and Detection Performance[J].IEEE Transactions on Signal Processing,2006,54(3):823-838.
[8] HAIMOVICH A M,Blum R S,CIMINI L J.MIMO Radar with Widely Separated Antennas[J].IEEE Signal Processing Magazine,2008,25(1):116-129.
[9] BEKKERMAN I,TABRIKIAN Target Detection and Localization using MIMO Radars and Sonars[J].IEEE Transactions on Signal Processing,2006,54(10):3873-3883.
[10]XU H,WANG J,YUAN J,et al.Colocated MIMO Radar Transmit Beamspace Design for Randomly Present Target Detection[J].IEEE Signal Processing Letters,2015,22(7):828-832.
[11]ZHANG W T,LOU S T,LI X J,et al.Tracking Multiple Targets in MIMO Radar Via Adaptive Asymmetric Joint Diagonalization[J].IEEE Transactions on Signal Processing,2016,64(11):2880-2893.
[12]AITTOMAKI T,KOIVUNEN V.Radar Waveform Sidelobe Level Optimality and Sampling[J].IEEE Signal Processing Letters,2016,23(3):1-1.
[13]SHI J,HU G,LEI T.DOA Estimation Algorithms for Low-angle Targets with MIMO Radar[J].Electronics Letters,2016,52(8):652-654.
[14]LIU H W,ZHOU S H,SU H T,et al.Detection Performance of Spatial-Frequency Diversity MIMO Radar[J].IEEE Transactions on Aerospace & Electronic Systems,2014,50(4):3137-3155.
[15]WANG B,CUI G,Yi W,et al.Adaptive Bayesian Detection using Polarimetric MIMO Radar in Spatially Heterogeneous Clutter[J].IEEE Signal Processing Letters,2013,20(20):547-550.
[16]ZHOU S H,LIU H.Space-Partition Based Target Detection for Distributed MIMO Radar[J].IEEE Transactions on Aerospace & Electronic Systems,2013,49(4):2717-2729.
[17]PETILLOT Y,CHAORAN D,THOMPSON J.Predicted Detection Performance of MIMO Radar[J].IEEE Signal Processing Letters,2008(15):83-86.
[18]AITTOMAKI T,KOIVUNEN V.Exploiting Correlation in MIMO Radar With Angular Diversity[C]//Proceedings of 43rd Asilomar Conference on Signals,Systems and Computers (ACSSC),2009:1191-1195.
[19]AITTOMAKI T,KOIVUNEN V.Target Detection and Positioning in Correlated Scattering Using Widely Distributed MIMO Radar[C]//Proceedings of International Radar Conference,European 2010:403-406.
[20]HE Q,BLUM R S.Diversity Gain for MIMO Radar Employing Nonorthogonal Waveforms[C]//IEEE International Symposium on Communications,Control and Signal Processing.,2010:1-6.
[21]AITTOMAKI T,KOIVUNEN V.Performance of MIMO Radar With Angular Diversity Under Swerling Scattering Models[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(1):101-114.
[22]CHEN H W,LIU Y X,YANG Z C,et al.Correlation Characteristics of Channels in MIMO Radar[J].Acta Electronica Sinica,2011,20(1):175-178.
[23]BODENHAM D A,ADAMS N M.A Comparison of Efficient Approximations for a Weighted Sum of Chi-squared Random Variables[J].Statistics and Computing,2016,26(4):917-928.
(责任编辑 杨继森)
New Detection Method for MIMO Radar Under Non-Ideal Conditions
CHEN Ming-jian, LONG Guo-qing, HUANG Zhong-rui
(Electronic Engineering Institute, Hefei 230037, China)
This paper studied the problem of target detection for the distributed multiple-input multiple-output (MIMO) radars under arbitrary waveform correlation and antenna spacing. Based on the Cholesky decomposition, a new detection method under the Neyman-Pearson criterion for distributed MIMO radar was proposed. Firstly, we analyzed the correlation between the distributed MIMO radar echo, and proposed maximum likelihood MIMO detection algorithm with arbitrary array configuration. Then, in order to solve the problem of the singular correlation matrix of the transmitted waveforms, Cholesky decomposition method was applied. The uniform model of sufficient statistics was presented for distributed MIMO radars under non-ideal conditions. An approximate closed form formula was derived to calculate the theoretical probability of detection with a given probability of false alarm for the distributed MIMO radar. Through simulation we can draw conclusions that the detection performance in high SNR deteriorates with the increased the correlation of spatial diversity channels and transmitted wave forms, but the detection performance in low SNR improves with the increased the correlation. Finally, the numerical simulation verifies the validity and correctness of the theoretical analysis.
distributed MIMO radar; related waveform; target scattering coefficient; test statistics; test statistic likelihood ratio detection
2016-09-20;
2016-10-12
安徽省自然科学基金项目(1608085QF140)
陈明建(1983—),男,讲师,主要从事雷达信号处理研究。
10.11809/scbgxb2017.02.018
陈明建,龙国庆,黄中瑞.非理想条件下分布式MIMO雷达目标检测[J].兵器装备工程学报,2017(2):75-81.
format:CHEN Ming-jian, LONG Guo-qing, HUANG Zhong-rui.New Detection Method for MIMO Radar Under Non-Ideal Conditions[J].Journal of Ordnance Equipment Engineering,2017(2):75-81.
TN95
A
2096-2304(2017)02-0075-07
