反步自适应控制
2017-03-16路晖,胡健,仇杨
路 晖,胡 健,仇 杨
(南京理工大学 机械工程学院,南京 210094)
【信息科学与控制工程】
反步自适应控制
路 晖,胡 健,仇 杨
(南京理工大学 机械工程学院,南京 210094)
为了克服齿隙对传动性能的影响,选取死区模型表达齿隙传动效应,依据自适应控制理论提出反步自适应齿隙补偿策略;齿隙模型中主、从动轮结合处存在阻尼系数和刚性系数等未知参数,对其进行了在线估计,并推导设计出每个参数的自适应律;利用Lyapunov稳定性理论,采用反步积分方法,通过逐步递推选取Lyapunov函数,设计了基于状态反馈的自适应控制器;理论分析以及对反步积分自适应补偿控制方法与传统PID控制方法对比仿真表明:该方法有效地消除了齿隙对伺服性能的干扰,提高了系统的跟踪精度和鲁棒性。
伺服系统;自适应控制;反步积分;齿隙补偿

1 问题描述
要消除齿隙非线性的不利影响必须进行有效的齿隙非线性补偿,要实现这一目的则需要建立有效的齿隙非线性模型。机械传动中齿隙示意图如图1。

图1 机械传动齿隙示意图

(1)


(2)
z=θe-iθs
2 系统模型


则τ(t)=kx3+cx4,它可表示系统受齿隙非线性影响的不同阶段轮齿间的传递力矩。选取x1,x2,x3,x4作为状态变量,系统的状态方程可表述为
(3)

在实际应用中,啮合齿数在0~2之间的交替变换以及温度、润滑、材料磨损等条件的变化都会导致齿隙及参数k、c发生变化,从而引起轮齿传递力矩变化。在控制系统设计中,必须考虑轮齿间传递力矩变化造成的危害。
3 反步积分控制器设计
3.1 控制器原理

3.2 控制器设计
根据反步法原理,设计步骤如下:
1) 设计虚拟控制量η1,定义系统输出误差e1为
e1=yd-x1
(4)
由式(3)中第1个关系式可知,为使系统输出逼近期望输出yd,可将x2作为虚拟控制量,令其期望值为η1,因此当设计η1如下式所示时,可使得e1能够渐近稳定地趋于零。
(5)
式(5)中k1>0为设计参数。
2) 设计虚拟控制量η2,设速度误差信号e2为
(6)

β=-a1x2+a3i[(k-1)x3+cx4]
(7)
(8)
(9)
由式(3)中第2个关系式可知,为使系统速度信号逼近期望值,可将a3ix3作为虚拟控制量,令其期望值为η2,若存在稳定的自适应律,则当设计η2如下式所示时,可使得e1及e2能够渐近稳定地趋于零。
(10)
式(10)中k2>0为设计参数。

e3=η2-a3ix3
(11)
由式(3)中第3和第4个关系式可知,选取I作为系统真实控制量,并设计控制输入I以及参数自适应律如式(12)所示时,可使得e1、e2及e3能够渐进稳定地趋于零,从而使整个系统能够渐近稳定地跟踪期望值。
(12)
定理1:选取x2作为虚拟控制量,当设计其期望值如式(5)时,可使e1能够渐近稳定地趋于零,从而使系统输出逼近期望输出yd。
定理2:选取a3ix3作为虚拟控制量,当设计其期望值如式(10)时,可使e1及e2能够渐近稳定地趋于零,从而使系统速度信号逼近期望值。
定理3:选取I作为系统真实控制量,当设计控制输入I以及参数自适应律如式(12)所示时,可使e1、e2及e3能够渐进稳定地趋于零,从而使整个系统能够渐近稳定地跟踪期望值。
3.3 稳定性证明
1) 定理1证明:
选取Lyapunov函数V1为
(13)
则V1的微分为
(14)
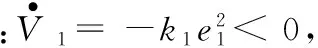
2) 定理2证明:
选取Lyapunov函数V2为
(15)
则V2的微分为
(16)

(17)
将式(17)代入式(16)得:
(18)
式(18)中:
将式(9)代入式(18)得:
(19)
3) 定理3证明:
选取Lyapunov函数V3为
(20)
则V3的微分为
(21)
式(21)中:
(22)
(23)
由式(8)求得式(23)中:
(24)
由式(3)求得式(24)中:
(25)
由式(24)和式(25)求得:
φx3-
(26)
由式(22)和式(26)最终求得:
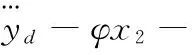
(27)
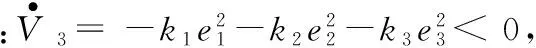
4 仿真结果分析
伺服系统中齿隙非线性造成的影响以及对反步积分自适应补偿算法的正确性验证,在被控对象和参考命令都相同的情况下,应用Matlab/Simulink对反步积分自适应补偿控制方法和PID控制方法进行对比仿真。伺服结构模型参数:Je=0.06 kg·m2,Js=0.18 kg·m2,be=1.7 Nms/rad,bs=1.8 Nms/rad,Kt=70,i=7,K=150 Nm/rad,c=0.17 Nms/rad;通过手工调校的方法,选定反步积分自适应控制参数如下:k1=30,k2=2,k3=5,r1=20,r2=0.015;PID控制参数调节如下:kp=80,ki=20,kd=40。
4.1 阶跃响应性能分析
通过系统的阶跃响应比较PID控制和反步积分自适应控制对系统性能的控制效果。图2(a)、图2(b)分别表示系统在PID控制和反步积分自适应控制作用下系统的阶跃响应,由图2可知,系统在反步积分自适应控制作用下的超调量比在PID控制作用下的小5%,由此说明在反步积分自适应控制作用下系统的平稳性更好。

图2 阶跃信号下系统的跟踪误差分析
4.2 正弦跟踪性能分析
为比较PID控制和反步积分自适应控制对系统性能的控制效果,引入类正弦输入信号yd=sint(1-exp(-0.01t3)),图3(a)、(b)与(c)、(d)分别表示在PID及反步积分自适应控制作用下系统对该类正弦输入的响应和跟踪误差。通过图3可以看出,在齿隙非线性的影响下,机电传动系统会引入稳态跟踪误差,使系统的控制效果下降、跟踪精度降低,但采用反步积分自适应控制方法考虑齿隙非线性因素进行控制律设计,有效抑制了齿隙影响,使跟踪误差显著减小,仅为PID控制下的1/5,使得控制效果得到显著提升。
图4(a)、(b)分别表示系统在PID控制与反步积分自适应控制作用下的控制输入。
从图4可以看出,当指令信号运动方向发生改变时,由于齿隙死区非线性的影响导致从动机构实际运动出现滞后,跟踪误差逐渐增大。由于PID控制不具备自适应能力,因此在PID控制下的传递力矩产生了剧烈的振荡,导致系统不稳定,而在反步积分自适应控制下,跟踪误差虽然出现小的跳变,但是其跟踪精度远高于PID控制方法,且其主动对齿隙进行补偿时,在齿隙作用阶段存在控制量激增的过程,使系统快速渡过齿隙阶段,消除齿隙影响,使传递力矩在跨越齿隙时连续平滑,避免了强烈的反复碰撞。因此采用自适应控制器能够在机电传动系统存在未知参数和齿隙死区非线性的情况下,高精度跟踪期望的位置信号,且齿轮的传递力矩连续平稳,具有良好的稳定性和鲁棒性。

图3 正弦信号下系统的跟踪误差分析

图4 系统自适应仿真分析
5 结论
本文针对基于齿隙传动的机电伺服作动系统中存在的齿隙非线性及参数不确定性问题,应用自适应控制理论和反步积分方法,设计了基于全状态反馈的自适应控制器,使系统能够渐进稳定地跟踪期望目标。仿真结果表明:与传统PID控制方法相比,该方法能够把系统的跟踪误差减小到2×10-4rad,轮齿平稳、连续地传递力矩,有效地消除了齿隙对伺服性能的干扰,提高了系统的跟踪精度和鲁棒性。
[1] 赵国峰.一类齿隙非线性控制系统的研究[D].南京:南京理工大学,2005.
[2] 朱胜,孙明轩,何熊熊.齿隙非线性输入系统的迭代学习控制[J].自动化学报,2011,37(8):1014-1017.
[3] 杜仁慧,吴益飞,陈威.考虑齿隙伺服系统的反步自适应模糊控制[J].控制理论与应用,2013,30(2):254-260.
[4] 李兵强,陈晓雷,林辉,等.机电伺服系统齿隙补偿及终端滑模控制[J].电工技术学报,2016,31(9):162-168.
[5] ZHOU J,ZHANG C J,WEN C Y.Robust Adaptive Output Control of Uncertain Nonlinear Plants with Unknown Backlash Nonlinearity[J].IEEE Transaction on Automatic Control(S0018-9286),2007,52(3):503-509.
[6] M.NORDIN,P.-O.GUTMAN.Controlling Mechanical Systems with Backlash-a Survey[J].Automatica,2012,38(10):1633-1649.
[7] LIU Y J,TONG S C.Adaptive Fuzzy Control for a Class of Nonlinear Discrete-time Systems with Backlash[J].IEEE Transactions on Fuzzy Systems,2014,22(5):1359-1365.
[8] WANG H Q,CHEN B,LIU K F,et al.Adaptive Neural Tracking Control for a Class of Nonstrict-feedback Sto-chastic Nonlinear Systems with Unknown Backlash-like Hysteresis[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(5):947-958.
[9] TARBOURIECH S,QUEINNEC I,PRIEUR C.Stability Aanalysis and Stabilization of Systems with Input Backlash[J].IEEE Transactions on Automatic Control,2014,59(2):488-494.
[10]MERZOUKI R,DAVILA J A,FRIDMAN L,et al.Backlash Phenomenon Observation and Identification in Electro-mechanical System[J].Control Engineering Practice,2007,15(4):447-457.
[11]陈卫东,唐得志,王海涛,等.基于Backstepping的机器人鲁棒跟踪控制[J].系统仿真学报,2004,16(4):837-841.
[12]胡建辉,邹继斌.永磁伺服同步电动机自适应反步控制的建模与仿真[J].系统仿真学报,2007,19(2):247-249.
[13]PHILIPP R,THOMAS B,MIROSLAV B,et al.Hybrid App-roach to Modeling Control and State Estimation of Mechanical Systems with Backlash[J].International Journal of Control,2007,80(11):1729-1740.
[14]ESBROOK A,TAN X,KHALIL H K.Self-excited Iimit-cycles in an Integral-controlled System with Backlash[J].IEEE Transactions on Automatic Control,2014,59(4):1020-1025.
[15]SHI Z G,ZUO Z Y.Backstepping Control for Gear Transmission Servo Systems with Backlash Nonlinearity[J].IEEE Transactions on Automation Science and Engineering,2015,12(2):752-757.
(责任编辑 杨继森)
Backstepping Adaptive Control
LU Hui,HU Jian,QIU Yang
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
In order to overcome the influence of the transmission performance of backlash, the dead zone model was selected to express the backlash transmission effect, and the adaptive control strategy based on adaptive control theory was proposed. The control laws based on state feedback were developed with backstepping approach for selecting appropriate Lyapunov function. Theory analysis and the backstepping integral adaptive compensation control method with the traditional PID control method were used to have simulation and comparison. Simulation results show the method effectively eliminates the backlash on the servo performance of interference, so as to improve the tracking accuracy and robustness of the system.
servo system; adaptive control; backstepping integral; backlash compensation
2016-09-12;
2016-10-15
国家自然科学基金项目(51505224;51505203);江苏省自然科学基金项目(BK20150776)
路晖(1988—),男,硕士研究生,主要从事机电控制研究。
10.11809/scbgxb2017.02.019
路晖,胡健,仇杨.反步自适应控制[J].兵器装备工程学报,2017(2):82-87.
format:LU Hui,HU Jian,QIU Yang.Backstepping Adaptive Control[J].Journal of Ordnance Equipment Engineering,2017(2):82-87.
TP273
A
2096-2304(2017)02-0082-06
