基于CEEMD-WPT的滚动轴承特征提取算法*

2017-03-15王丽华陶润喆张永宏赵晓平谢阳阳

振动、测试与诊断 2017年1期

关键词：特征频率频谱分量

王丽华，陶润喆，张永宏，赵晓平，谢阳阳

(1.南京信息工程大学信息与控制学院南京，210044)(2.南京信息工程大学江苏省网络监控中心南京,210044)

基于CEEMD-WPT的滚动轴承特征提取算法*

王丽华1，陶润喆1，张永宏1，赵晓平2，谢阳阳1

(1.南京信息工程大学信息与控制学院南京，210044)(2.南京信息工程大学江苏省网络监控中心南京,210044)

为实现对滚动轴承振动信号中特征频率成分的精确提取，提出了将互补总体平均经验模态分解(complementary ensemble empirical mode decomposition,简称CEEMD)与小波包变换(wavelet package transform,简称WPT)相结合即CEMMD-WPT特征信号提取算法。两种方法的结合既有效解决了CEEMD分解后依然存在的模态混叠问题，又消除了进行WPT处理后产生虚假频率分量、频率混淆现象的影响。通过仿真试验验证了该方法的有效性，并应用于实际，取得很好的结果。

滚动轴承; 小波包变换; 互补总体平均经验模态分解; 特征提取

引言

滚动轴承是旋转机械中应用最广但最易损坏的机械零件，其工作好坏直接影响机械的工作状态，故对滚动轴承振动信号中的特征成分实现精确提取十分重要。由于机械设备振动信号多为非线性非平稳信号，时频分析方法如小波变换(wavelet transform,简称WT)、希尔伯特黄变换(Hilbert-Huang transform,简称HHT)和Gabor变换等。由于能够同时提供时域信号和频域信号的局部信息，因此得到广泛应用。文献[1]提出了一种基于连续小波的信号检测和故障诊断的方法，但不管是小波还是小波包变换，在实际应用中都会在频段分割处产生频率混淆、虚假分量现象，且不具有自适应性[2]，直接用于特征信号的提取效果不佳。近年来，随着希尔伯特黄变换的提出，经验模态分解(empirical mode decomposition,简称EMD)得到推广应用。EMD分解出的固有模态函数(intrinsic mode function,简称IMF)包含原信号不同时间尺度的局部特征[3]。通过对各IMF变化的监测可以实现对滚动轴承状态的监测[4]。EMD存在严重的模态混叠的缺点[5]，无法实现对特征的精确提取。针对模态混叠的缺点，陈建国等[6]提出了采用独立分量分析(independent component analysis，简称ICA)来抑制模态混叠的方法，但 ICA的幅值不确定性大大影响了结果的精确性。Wu等[7]通过研究白噪声信号的统计特征，提出了总体平均经验模态分解(ensemble empirical mode decomposition,简称EEMD)，取得了一定的抑制效果，但仍无法完全消除，且分解过程中每次添加的白噪声可能会引起重构误差[8]。雷亚国等[9]根据Wu的算法提出了一种自适应的EEMD并应用在行星齿轮箱故障检测中，进一步削弱了模态混叠的现象，但仍继承了EEMD分解后得到的分量未必满足IMF定义的缺陷、且增加了分解过程中的计算量。Yeh等[10]在EEMD的基础上提出了CEEMD，解决了重构误差问题。到目前为止，在实际应用中想要完全避免模态混叠，实现对特征信号的精确提取，仍然是没有得到解决的问题[11]。

为了消除CEEMD分解后依然存在的少量模态混叠问题，实现对工作信号中特征频率成分的精确提取，笔者提出将CEEMD和WPT相结合的特征提取算法。利用WPT的局部分析能力对CEEMD分解后依然存在的模态混叠部分予以修正，并消除WPT处理时再次产生频率混淆、虚假分量现象的影响，从而实现特征信号的精确提取。

1 算法描述

1.1 CEEMD分解

CEEMD是基于EMD和EEMD提出的一种改进算法。EMD[3]是一种自适应的局部化分析方法，它从原信号中分解出的IMF突出了数据的局部特征，从根本上摆脱了傅里叶变换的局限性，适用于非平稳、非线性信号的处理，但EMD会出现模态混叠现象。模态混叠是指同一IMF分量包含了不同的时间尺度分量(不同的频率成分被分解到同一IMF内，或同一频率成分被分解到不同的IMF内)[12]，产生模态混叠的原因主要有:a.噪声干扰，改变了信号原本的极值点分布；b.信号中含有间断高频弱信号成分；c.信号中各成分的频率过于接近。针对EMD的缺陷，EEMD[7]被提出，其利用白噪声频谱的均匀分布特性，使混入白噪声的信号在不同时间尺度上具有连续性，在一定基础上抑制了模态混叠问题，但由于分解时添加的白噪声会引起重构误差，提取的信号幅值也会被改变。

采用CEEMD对信号进行自适应分解，提取特征频率信号的效果最好，其与EEMD的主要区别是通过向信号中添加两个相反的白噪声信号，并分别进行EMD分解，从而消除了EEMD分解中添加白噪声的影响，具体步骤[13]如下。

1) 分别向被分析信号x(t)中加入等长度的、给定标准差的、一组符号正负相反的正态分布白噪声，形成两个新信号；

2) 应用EMD对加入白噪声后的两个信号分别进行分解，得到其各自的IMF分量；

3) 重复n次步骤1和步骤2，要求每次加入新的随机正态分布白噪声序列；

4) 将每次分解得到的分量共计2n组IMFs对应相加后(如第1次分解的IMF1加上第2次分解IMF1，直到2n组IMF1相加)再分别除以2n求其平均，得到一组IMF分量即为分解结果。

y1=sin(20πt) (0≤t≤1)

(1)

(2)

仿真信号采样频率为1 kHz，采样时间为1 s。分别采用EMD和CEEMD对仿真信号s(t)进行分解，n为50次，k为0.1倍，结果如图1，2所示。

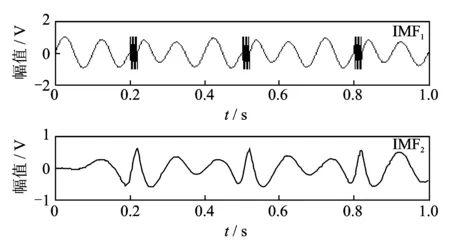
图1 仿真信号EMD分解的前2个IMF分量Fig.1 The former two IMF components after EMD

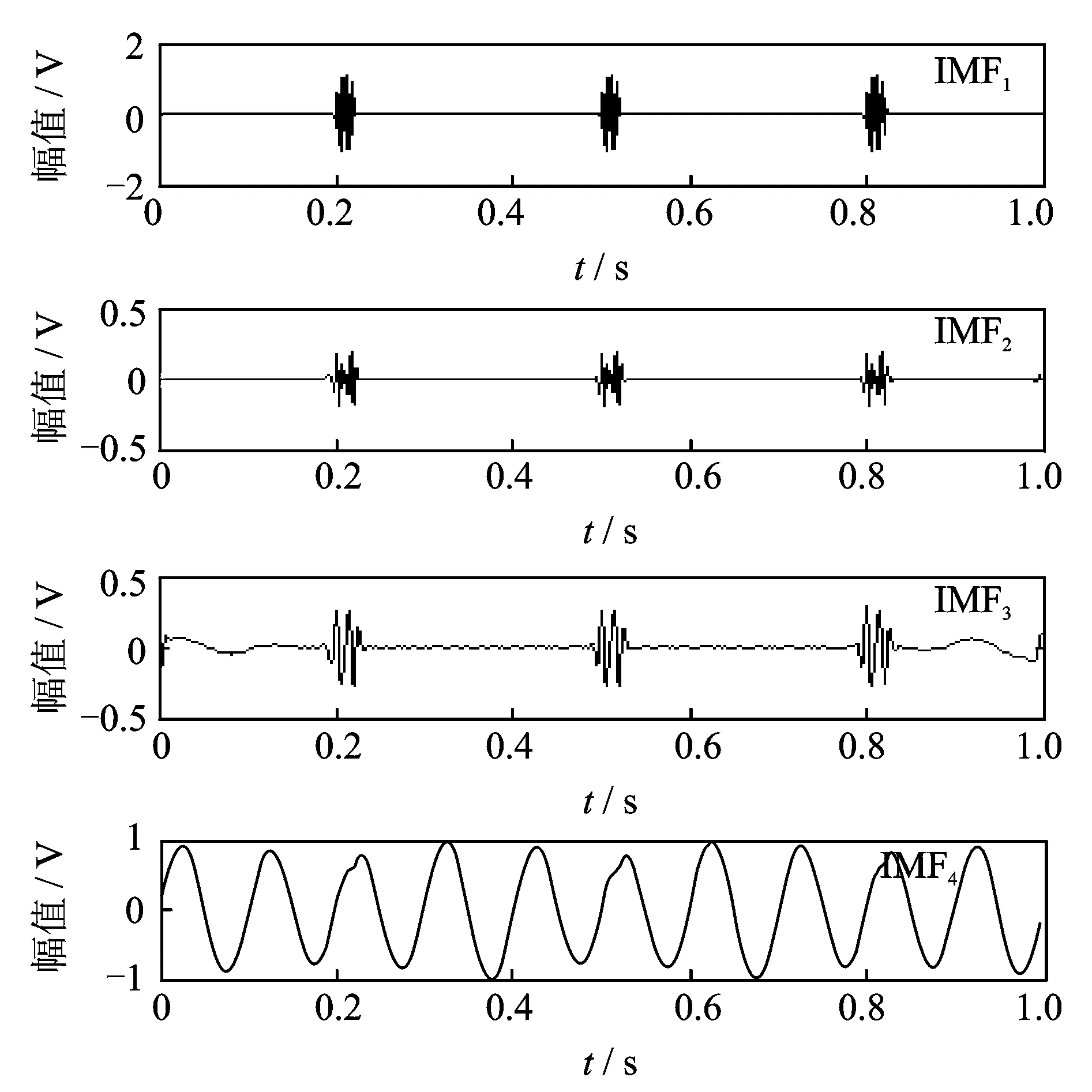
图2 CEEMD分解的前4个IMF分量Fig.2 The first four IMF components after CEEMD

由图1可见，两个频率相差很大的信号并没有被自适应分开，出现了模态混叠现象。

由图2看出，CEEMD分解得到的IMF1较好地提取出高频间断信号，IMF1和y2(t)做相关性分析可以达到91.12%；但IMF2，IMF3依然出现了少量的模态混叠现象；IMF4提取出低频正弦信号。

综上所述，使用CEEMD自适应提取特征频率分量虽在一定基础上抑制了模态混叠的问题，但依然没有实现精确提取。

1.2 小波包变换

为了消除CEEMD分解后依然存在的模态混叠问题，实现对特征信号的精确提取，笔者对分解后存在模态混叠的部分利用WPT进行修正。WPT是WT的推广，其实质是对信号的多带通滤波处理。与WT不同的是，WPT在对信号的低频部分进行分解的同时，对高频部分也进行了分解，具有更好的局部分析能力[14]。但在实际特征提取中，小波包滤波器的频域特性并不理想，分解过程中对信号进行隔点采样，采样频率的减半往往会引起频率折叠。另外，在重构过程中的隔点插零又使采样频率加倍，因此整个分解、重构过程易造成频率混淆现象，且子带易产生虚假频率分量。单独运用WPT进行特征频率信号的提取，往往会因为频率混淆、虚假分量的产生，降低结果的精确度。故笔者提出将CEEMD与WPT相结合，实现滚动轴承特征频率信号的精确提取。

2 基于CEEMD-WPT的特征提取算法

对采集的振动信号进行CEEMD自适应分解，得到不同的IMF分量，每个IMF对应一个频率段，此时针对所需提取的特征信号找到所在的IMF即可。若特征信号出现模态混叠则进行修正：因分解后的IMF内主频率成分的幅值大于分量内混叠部分的频率幅值，且只含有相应频段内的成分，故此时利用WPT进行模态混叠部分的特征分量提取可以有效消除子频带产生频率混淆、虚假分量的影响，实现对特征信号的精确提取，即笔者提出的CEEMD-WPT算法，具体算法流程如图3所示。

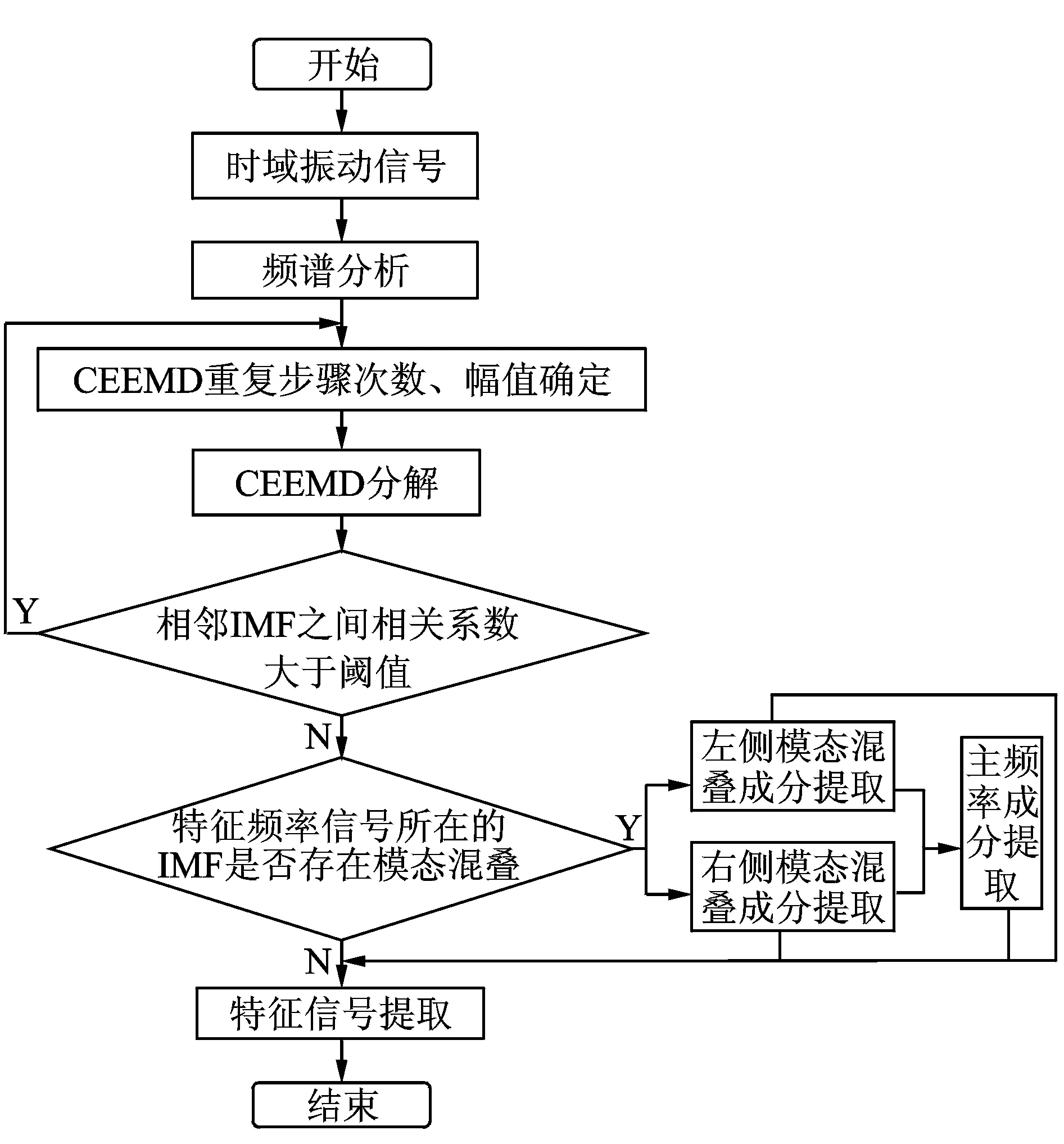
图3 CEEMD-WPT算法流程图Fig.3 Flow chart of CEEMD-WPT method

1) 对振动信号做频谱分析，确定信号噪声的大小以及各频率成分的幅值大小。

2) 根据信号中所含噪声的大小，确定CEEMD分解次数和白噪声幅值，信号内所含噪声越大，k的取值大。文中选择标准差倍数k为0.1～0.3，重复步骤次数n一般选择百以内即可。

3) 进行CEEMD自适应分解。

4) CEEMD分解得到的各IMF分量自适应提取出各频段分量，对每个IMF做出其频谱图，检查是否出现频率混叠，并对每个相邻的IMF分量做相关性分析，相关性数值超过阈值(阈值根据实际分解自行设定，一般设定为30%，若在低频段出现过分解，此时低频段IMF之间相关系数较大，可调大阈值)，就认为存在严重的模态混叠，重新调整n和k，重复步骤3和4；若小于阈值，执行步骤5。

5) 检查特征频率信号是否存在模态混叠。若出现了少量的模态混叠的现象，则利用WPT予以修正，将特征频率分量从混叠的IMF内提取出来。IMF为某一频段的分量，此时频段内所含的成分较少且主频率成分(f)在中间，模态混叠部分(f1，f2)分别分布于主频率的两侧，利用WPT进行模态混叠的修正，分为以下3种情况：a.若所需提取的特征分量为左侧的f1，因IMF只含有某一频段的分量，此时只需将高于特征分量的频率成分进行剔除即可；b.若所需提取的特征分量为右侧的f2，此时只需将低于特征分量的频率成分进行消除；c.若所需提取的特征分量为主频率成分f，首先需提取出f1和f2，再用IMF减去提取出的f1和f2即可得到。

以情况1为例对具体实现过程进行描述：a.因对f1进行WPT提取，则小波包频段分割的下限需低于f1，而上限需尽可能高于f1且低于需剔除的频率；b.在提取的过程中，因在频段分割的上限邻近处有需剔除的频率成分，则WPT提取后易再次产生频率混淆现象并含有虚假分量，提取的结果为M1，此时需将M1中再次产生的频率混淆和虚假分量进行消除；c.采取的方法为调整频段分割的下限尽可能高于f1且低于虚假分量的频率，上限不变，然后对IMF再次进行WPT提取得到M2，M2中同样会产生混淆部分和虚假分量;d.故用两次提取的结果进行相减M=M1-M2，消除WPT产生的频率混淆、虚假分量现象，很好地将特征频率分量从模态混叠的IMF内提取出来。

6) 将同一特征频率分量从不同的IMF内提取出来进行时域上的相加，从而实现对特征信号的精确提取。

3 仿真实验及工程应用

3.1 仿真实验

3.1.1 混合信号仿真

旋转机械的振动信号中存在各部件正常工作运行信号、故障信号及环境噪声等多种信号，仿真一个由以下4 种基本信号耦合形成的混合信号Signal[9]。S1,S2模拟设备正常运行信号；S3模拟碰摩故障发生时的特征信号；Noise模拟噪声信号。设采样频率为1 kHz，采样时间为1 s，信号模型为

(3)

混合信号为

Signal=S1+S2+S3+Noise

其中：正弦信号S1频率为100 Hz，振幅为1 V(如图4(a)所示)；余弦信号S2频率为10 Hz，振幅为1.5 V，初相位为1.5cos(-10)(如图4(b)所示)；频率为2.5 Hz、振幅为2 V的正弦信号与频率为30 Hz、振幅为1 V的余弦信号相乘得到S3(如图4(c)所示)；振幅为2.5 V的随机信号模拟噪声Noise如图4(d)所示。

图4 混合信号SignalFig.4 Mixed signal

源信号及混合信号时域波形如图4所示。混合信号的频谱如图5所示。

图5 混合信号频谱图Fig.5 Mixed signal spectrum

图6 CEEMD-WPT得到IMF3时域图Fig.6 The IMF3 component after CEEMD-WPT

3.1.2 CEEMD-WPT特征提取

采用CEEMD-WPT算法提取故障信号S3。经过算法步骤1～4，选择n为100，k为0.2倍。因篇幅限制，在仿真部分直接给出CEEMD-WPT分解后提取故障特征信号的结果，WPT修正IMF的部分在实际工程应用中再具体说明。CEEMD-WPT算法得到的第3个IMF分量为故障信号S3，如图6所示。

为验证分解的效果，检查是否还存在模态混叠的部分，对IMF3做频谱分析，如图7所示。可以看出，特征频率信号已经很好地提取出来，对IMF3与其相邻的IMF分量做相关性分析，数值都在0.01以下，有效解决了模态混叠的问题，且IMF3与源信号S3的相关性数值达到98.02%，故CEEMD-WPT很好地对特征频率信号进行了提取。

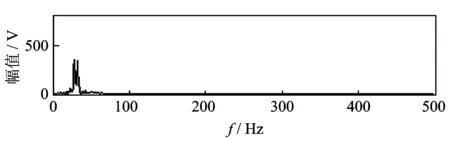
图7 IMF3分量频谱图Fig.7 The IMF3 component spectrum

采用带通滤波的方法同样对特征信号S3进行提取，两者结果进行对比，选择带通滤波的范围为20～40 Hz，提取结果的时域图如图8所示。

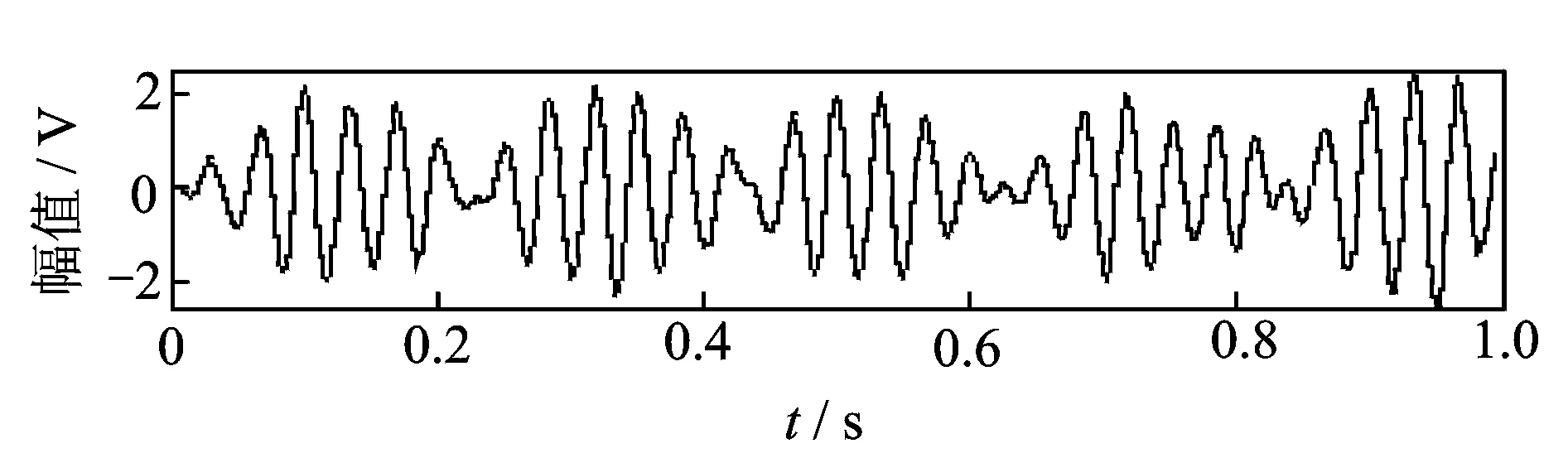
图8 带通滤波提取S3的时域图Fig.8 S3 time domain map extracted with band-pass filter

带通滤波的结果与源信号S3做相关性分析，数值为86.35%，由图8可看出，带通滤波提取的结果没有CEEMD-WPT提取的结果精确，原因在于并不存在理想的带通滤波器，滤波器不能将期望频率范围外的所有频率完全滤去，在所需提取的频率带外还有一个没有被滤去，但被衰减的范围即滚降现象。故滤波器的设计尽量保证滚降范围越窄越好，然而随着滚降范围越来越小，通带就变得不再平坦，开始出现“波纹”。这种现象在通带的边缘处尤其明显，滤波后易造成信号时域分布的改变。因此，当信号中频率成分过于靠近时，使用滤波的方法无法实现精确提取。

3.2 工程应用

采用OROS R3X系的动态信号分析仪对卧式螺旋离心机(简称卧螺离心机)运行阶段的振动信号进行采集[15]。卧螺离心机相关参数如表1所示。

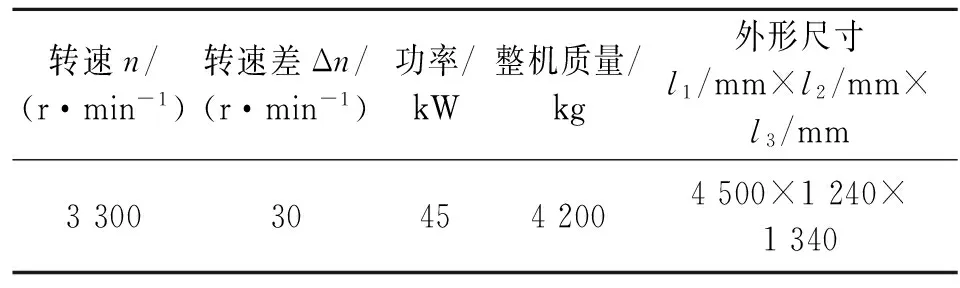
表1 卧螺离心机主要技术参数

振动传感器布置在左右轴承座，从水平和垂直两个方向测量大端和小端瓦振；在大端和小端都安装支架固定电涡流传感器用来测量轴的振动；光电传感器安装于转鼓大端。传感器的布置如图9所示。

图9 卧螺离心机大端传感器布置Fig.9 The sensor arrangement

取大端垂直方向轴振工作阶段的振动信号为例，采样频率为12.8 kHz，采样时间为20 s，图10为其时域信号。采用CEEMD-WPT算法对卧螺离心机工作频率即1阶特征分量55 Hz进行提取。

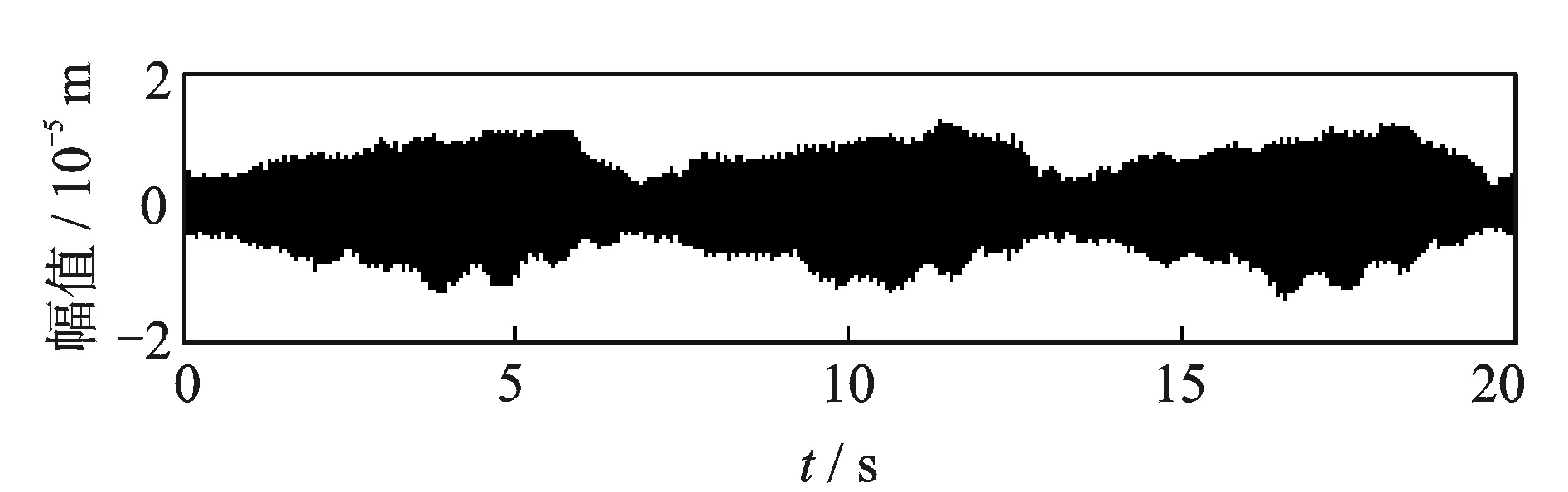
图10 振动信号时域图Fig.10 Time domain diagram of vibration signal

由图11看出,振动信号由多个频率成分组成，且只含有少量的噪声，利用CEEMD-WPT算法对特征频率信号55 Hz进行提取，经过算法选择n为50次，k为0.1倍。由于CEEMD自适应分解后的IMF分量是根据频率段从高到低依次排列下来，因篇幅限制，笔者只列出分解后特征频率信号55 Hz存在模态混叠的两个IMF分量(IMF7，IMF8)频谱图，如图12所示。

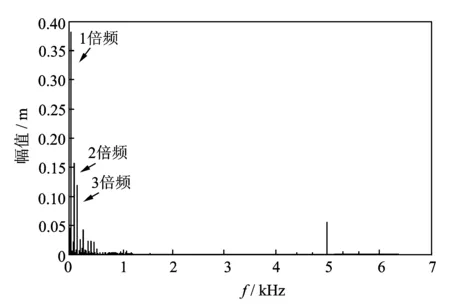
图11 振动信号频谱图Fig.11 Spectrum of vibration signal

由图12可以看出，CEEMD分解后在低频部分(图中圆圈处)依然出现了少量的模态混叠，55 Hz特征频率信号被分解在IMF7，IMF8中。为了实现对特征频率信号的提取，需对分解后的IMF7，IMF8进行WPT修正，首先需要将IMF7中的左侧模态混叠部分f1(55 Hz)分量提取出来，由于采样频率为1.28 kHz，而55 Hz分量十分靠近WPT7层分解的50 Hz频段分割处，直接进行WPT提取无法实现，根据算法步骤5的第1种情况，首先对IMF7进行WPT6层分解，采用将100 Hz以上的频率成分剔除，提取出0～100 Hz频段的分量M1，如图13所示。

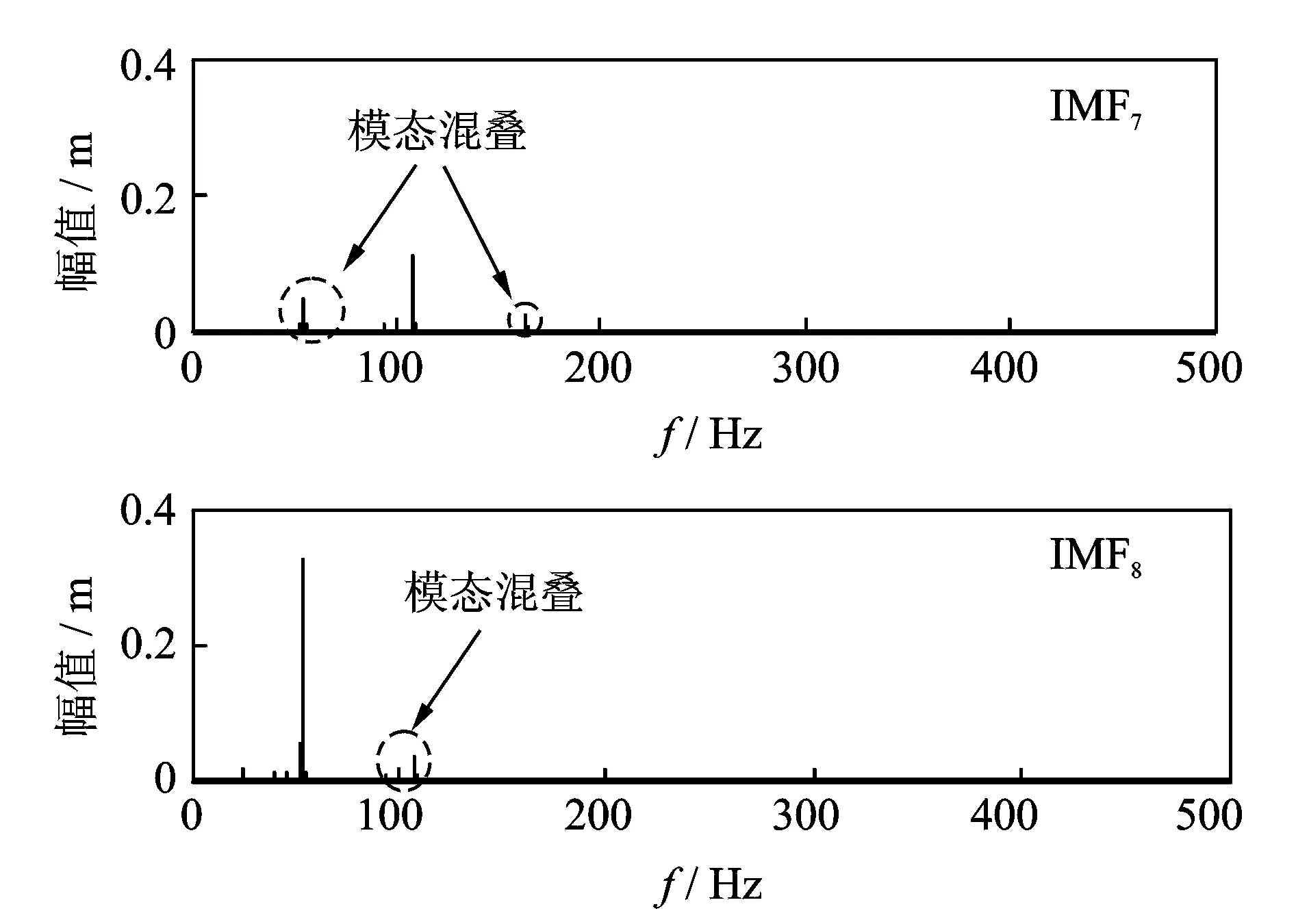
图12 IMF7，IMF8分量频谱图Fig.12 The IMF7，IMF8 components spectrum

图13 IMF7经过6层WPT提取的0～100 Hz分量频谱图Fig.13 IMF7 after 6 level of WPT extracted 0～100 Hz component spectrum

由图13可看出，在靠近频段分割上限处100 Hz的地方存在2倍频110 Hz分量，M1中出现了频率混淆的现象并产生了虚假分量(图13圆圈中)，则对特征分量的精确提取产生影响，需将其消除。再次对IMF7进行8层分解，提取出75～100 Hz的频段M2，如图14所示。由于IMF7中的55 Hz分量幅值较小，且离WPT8层分解的频段分割的下限处75 Hz较远，此时分解所产生的虚假分量与6层分解所得到的相同。

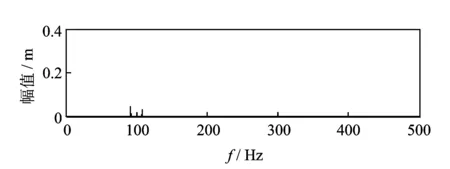
图14 IMF7经过8层WPT提取的75～100 Hz分量频谱图Fig.14 IMF7 after 8 level of WPT extracted 75～100 Hz component spectrum

用WPT6层分解得到的结果M1(如图13所示)减去WPT8层分解的结果M2(如图14所示)，从而消除WPT提取时产生的虚假分量、频率混淆现象的影响，此方法有效地将55 Hz分量从模态混叠的IMF7中提取出来，其频谱图如图15所示。

图15 IMF7经过WPT提取的55 Hz分量频谱图Fig.15 IMF7 after WPT extracted 55 Hz component spectrum

同样将模态混叠的IMF8中主频率成分f(55 Hz)提取出来，将IMF7，IMF8中提取的分量进行相加，提取的1阶特征信号频谱图如图16所示。

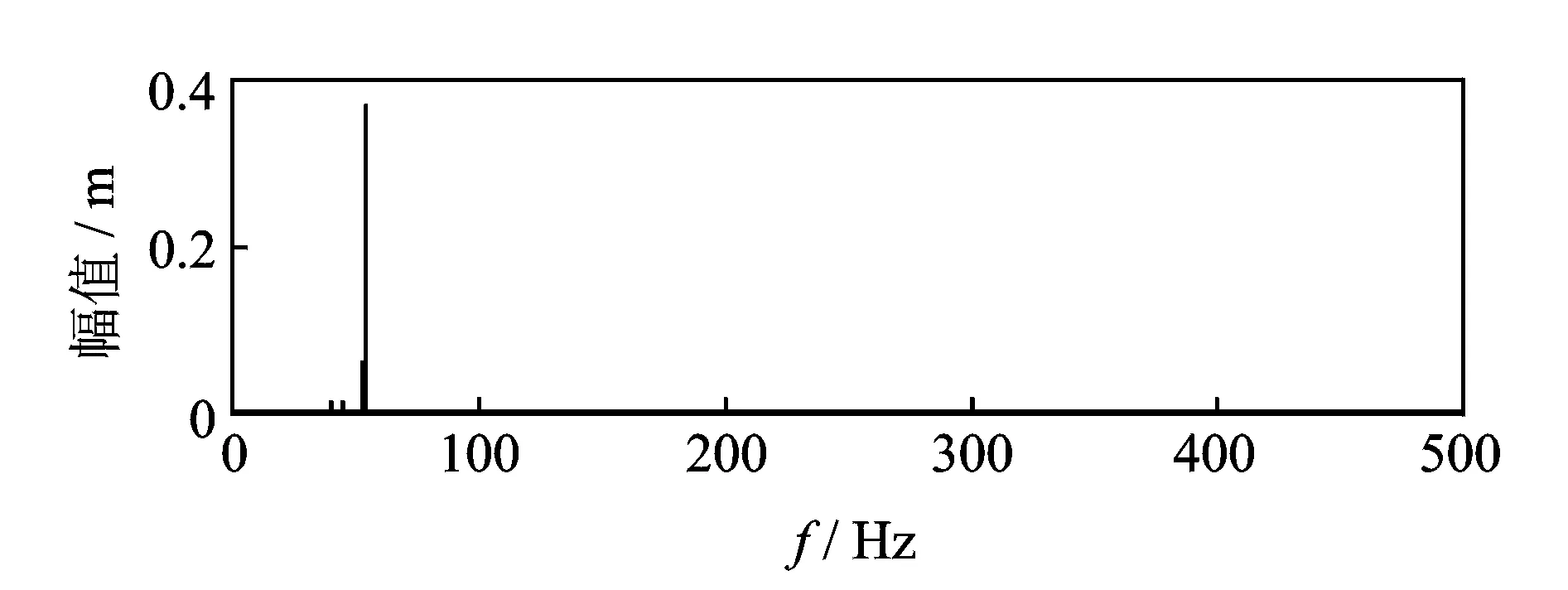
图16 CEEMD-WPT提取的信号频谱图Fig.16 CEEMD-WPT extraction of the signal spectrum

由图16可以看出，将模态混叠部分进行了较好的消除，有效地提取出特征频率信号。运用WPT，CEEMD以及CEEMD-WPT算法提取特征信号，结果比较如图17所示。

图17 WPT，CEEMD，CEEMD-WPT提取特征时域图Fig.17 WPT,CEEMD,CEEMD-WPT extraction characteristic time domain diagram

由图17可以看出，CEEMD-WPT提取的特征信号与WPT单独提取的相比信号的幅值较小，但更加的平滑。原因在于WPT实质就是多带通滤波，但不管是高通、低通、带通滤波，在实际应用中并不存在理想的滤波器，在通带和阻带之间都存在一个频率成分不会被完全抑制、只是衰减的过渡带。故利用滤波的方法去实现特征信号的精确提取是比较困难的。CEEMD-WPT与CEEMD提取的结果相比，信号完整，更具有周期性，CEEMD存在模态混叠的问题，导致分解得到的IMF不一定能实现单一频率信号的精确提取。故利用CEEMD-WPT算法提取的特征信号最精确，不仅对特征信号可以实现自适应提取，也有效解决了分解后出现模态混叠的问题，便于后期的状态监测及故障诊断。

4 结论

1) 详细阐述了HHT中EMD信号处理方法的优点以及缺陷，针对EMD的模态混叠问题引入CEEMD，简要介绍了WPT以及传统的滤波思想。

2) CEEMD自适应分解虽然有效改善了EMD在含有间断点信号中的模态混叠问题，但在实际应用中依然存在少量的频率混叠部分。WPT及传统的滤波方法可以实现对信号局部特征的提取，但也无法做到精确提取。针对CEEMD，WPT两个信号处理方法的优缺点进行结合，实现对特征频率信号的精确提取。

3) 运用CEEMD-WPT算法对实际工程信号进行特征信号提取，通过与计算所得的频率进行对比，良好地实现了精确提取，为后期的状态检测与故障诊断打下基础。

[1] 林京, 屈梁生. 基于连续小波变换的信号检测技术与故障诊断[J]. 机械工程学报, 2000, 36(12): 95-100.

Lin Jing, Qu Liangsheng. Feature detection and fault diagnosis based on continuous wavelet transform[J]. Journal of Mechanical Engineering, 2000, 36(12): 95-100. (in Chinese)

[2] 秦毅, 秦树人, 毛永芳. 小波变换中经验模态分解的基波检测及其在机械系统中的应用[J]. 机械工程学报, 2008, 44(3): 135-142.

Qin Yi, Qin Shuren, Mao Yongfang. Fundamental wave detection based on wavelet transform and empirical mode decomposition with application in mechanical system[J]. Journal of Mechanical Engineering, 2008,44(3): 135-142. (in Chinese)

[3] Huang N E, Shen Z, Long S.R The empirical modedecomposition method and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Societyof london,Series,1998(454): 903-995.

[4] 杨宇, 于德介, 程军圣. 基于EMD与神经网络的滚动轴承故障诊断方法[J]. 振动与冲击, 2005, 24(1): 85-88.

Yang Yu, Yu Dejie, Cheng Junsheng. Roller fault diagnosis method based on EMD and Neural network[J]. Journal of Vibration and Shock, 2005, 24(1): 85-88. (in Chinese)

[5] 曹莹,段玉波,刘继承.Hilbert-Huang变换中的模态混叠问题[J].振动、测试与诊断,2016,36(3):518-523.

Cao Ying, Duan Yubo, Liu Jicheng. Research and application of mode-mixing in Hilbert-Huang transform[J]. Journal of Vibration,Measurement & Diagnosis,2016,36(3):518-523. (in Chinese)

[6] 陈建国,张志新,郭正刚.独立分量分析方法在经验模态分解中的应用[J].振动与冲击, 2009,28(1):109-111.

Chen Jianguo, Zhang Zhixin, Guo Zhenggang. Application of independent component analysis in empiricalmode decomposition[J]. Journal of Vibration and Shock, 2009,28(1):109-111. (in Chinese)

[7] Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[8] 陈隽,李想.运用总体经验模式分解的疲劳信号降噪方发[J].振动、测试与诊断,2011,31(1):15-19.

Chen Jun, Li Xiang. Application of ensemble empirical mode decomposition to noise reduction of fatigue signal[J].Journal of Vibration,Measurement & Diagnosis,2011,31(1):15-19. (in Chinese)

[9] 雷亚国,孔德同,李乃鹏.自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].机械工程学报,2014,50(3):64-70.

Lei Yaguo, Kong Detong, Li Naipeng. Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of Mechanical Engineering, 2014,50(3):64-70. (in Chinese)

[10]Yeh J R, Shieh J S. Complementary ensemble empirical mode decomposition: a noise enhanced data analy-

sis method[J]. Advances in Adaptive Data Analysis, 2010,2(2):135-156．

[11]Huang N E, Shen S . Hilbert-Huang transform and its applications[M]. Singapore: World Scientific Publishing Copteltd, 2014:22-24.

[12]胡爱军,孙敬敬,向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断,2011,31(4):429-434.

Hu Aijun, Sun Jingjing, Xiang Ling. Mode mixing in empirical mode decomposition[J]. Journal of Vibration,Measurement & Diagnosis,2011,31(4):429-434. (in Chinese)

[13]郑近德,潘海洋.APEEMD及其在转子碰摩故障诊断中应用[J].振动、测试与诊断,2016,36(6):257-263.

Zheng Jinde, Pan Haiyang. Adaptive partly-ensemble empirical mode decomposition and its application forrotor rubbing fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis,2016,36(6):257-263. (in Chinese)

[14]高英杰,孔祥东.基于小波包分析的液压泵状态监测方法[J].机械工程学报,2009,45(8):80-88.

Gao Yingjie, Kong Xiangdong. Wavelet packets analysis based method for hydraulic pump condition monitoring[J]. Journal of Mechanical Engineering, 2009,45(8):80-88. (in Chinese)

[15]赵晓平,侯荣涛.基于Viterbi算法的Gabor阶比跟踪技术[J].机械工程学报,2009,45(11):247-252.

Zhao Xiaoping, Hou Rongtao. Gabor order tracking based on viterbi algorithm[J]. Journal of Mechanical Engineering, 2009,45(11):247-252. (in Chinese)