恒速状态移动质量作用的柔性梁最优振动控制*

刘骁骁, 任兴民, 陈 虎, 杨永峰, 邓旺群, 任建亭

(1.西北工业大学力学与土木建筑学院 西安,710129) (2.中国航空动力机械研究所 株洲,412002)

恒速状态移动质量作用的柔性梁最优振动控制*

刘骁骁1, 任兴民1, 陈 虎1, 杨永峰1, 邓旺群2, 任建亭1

(1.西北工业大学力学与土木建筑学院 西安,710129) (2.中国航空动力机械研究所 株洲,412002)

针对恒速状态移动质量作用下柔性梁的最优振动控制方案进行研究分析。根据柔性梁振动理论，考虑移动质量与柔性梁弹性振动之间的耦合作用，建立移动质量-柔性梁时变系统的振动方程。当移动质量刚好离开梁时给出终端时刻点，超越终端时刻的梁作自动振动，建立时不变系统的振动方程。若将以往适用时不变系统的最优控制方法应用于时变系统，会导致次优化效果。为此，采用多种控制设计方法对系统的振动响应进行抑制，讨论不同控制方案的优缺性。数值结果表明：对于特定的作动器位置，有必要采用具有时变特征的控制方法替代时不变控制方法；相比时变控制方法，采用状态相关的黎卡提方程(state-dependent riccati equation, 简称SDRE)控制方法得到的性能指标最优；基于增广矩阵的线性二次型调节器(linear quadratic regulator,简称LQR)边界控制效果优于bang-bang控制，前者控制策略得到的性能指标最优。

移动质量； 柔性梁； 振动； 最优控制； 时变系统； 终端时刻

引 言

随着尺寸和重量限制的加强，舒适性和安全性又难以同时达到满足要求的情况下，柔性结构的振动控制受到越来越多的关注。控制设计方法通常希望能够表征特定加载条件下结构的动态行为。已有大量工作针对柔性结构的不同控制方法及控制方案的可行性进行了研究[1-3]。常见的有模态控制方法[4]、基于线性二次型控制方法[5]、适用于对称和非对称系统的极点重置和极点相消算法[6-7]以及考虑系统不确定性的鲁棒控制[8]。Deng等[9]提出将基于在线识别的模态控制方法运用于时变系统，并将已识别模态用于控制器的设计。

基于设计的线性二次型控制方法应用较为普遍， 文献[10]指出该方法容易降低对峰值响应的抑制效果，研究了bang-bang控制器的适用性。Bang-bang开关控制只需提供极值控制力，相比随着状态变化的线性二次型控制器，该方法更具速效性。实际上，修正的线性二次型控制准则有利于诸多目标的控制。Kim等[11]提出基于设计的二次型性能指标。针对最优控制问题，文献[12]提出了非二次型性能指标。

移动质量/荷载作用于梁是柔性结构控制中的一种特殊例子，通常该类问题的研究有据可循。对于车辆通过桥梁或弹丸离开身管的过程，国内学者将其简化为移动质量-梁模型进行分析[13-14]。在支撑结构的特定方面，提出的某些减振方案是被动的[15-16]，但理论模型要求具有广泛的实际应用。一般基础性的移动-载荷问题可参见文献[17]。Sung[18]采用两个压电作动器对移动质量作用下梁的振动进行控制，最优二次型指标泛函的最小值决定两作动器的不同位置。基于二次型性能指标的梁-移动质量控制问题参见文献[19]，文献中假定位移-速度反馈控制器的状态变量具有完备信息，并基于时变矩阵的代数黎卡提方程设计该控制器。文献[20]基于相同的性能指标，设计一组恒定增益状态反馈控制器，使弹性基础梁的横向挠度趋于最小化。文献[21]采用具有功率流的主动控制器对移动载荷-梁的响应进行抑制。基于时不变黎卡提矩阵，Mofid等[22]研究了带有压电-陶瓷作动器的多移动质量-梁最优控制问题。

对于基础性的动力系统控制问题可分为两个子问题：a.当移动质量在梁上运动时，是与持续时间对应的时变系统；b.移动质量离开梁后的时不变系统。相比其他结构控制问题，移动质量-梁系统的第1子问题可使最优控制理论更容易应用。尽管该运动方程具有时变系数，但仍有线性优势，该方法的另一优势存在着移动质量离开梁时的终端时刻。Naidu[23]指出此类最优问题可转化为固定的终端时刻问题。由于现有作动装备的局限性，文献[24]认为对控制力的幅值应考虑约束条件。需要强调的是，一旦定义最优控制问题，则最优方案仅关于性能指标最优，但也许不是结构工程师寻找的最优方案。例如，线性二次型指标在输出理论上强调控制的重要性，但通常预先确定恒定增益矩阵，控制过程中可能考虑不到动力解决方案的所有方面；对于移动质量-梁问题，若控制工程师对梁中跨响应感兴趣，当移动质量接近中跨时，会考虑采用能够提高控制效果的时变性能指标；当移动质量在作动点上方运动时，可考虑采用降低或增强控制作用的性能指标。

对于一般基础性的移动质量-梁问题，普遍考虑时不变控制问题，笔者则针对存在的两类子问题进行研究。基于时变系统的状态空间方程，定义最优控制问题，将其转化为时变线性二次型问题，给出同时考虑状态变量和控制变量的二次型性能指标泛函，分析一系列最优控制方法。将这些方法应用于上述子问题，控制目标定义为梁中跨挠度的最小值，通过控制目标，对比几种时变最优控制方案的优缺性，寻求关于性能指标最优的控制策略并尽可能接近最优理论解。

1 理论方法

1.1 线性系统的最优控制

对于受控的线性结构系统，时变状态空间方程及给定的初始状态为

(1)

其中：F(t)为输入力向量。

当处理移动质量作用下柔性梁的控制问题时，控制目标定义为特定位置下支承结构的中跨挠度最小值。此外，由于实际的控制解决方案存在局限性，需对控制变量U(t)进行约束，即|U(t)|≤U。若系统输出为y(t)=C(t)Z(t)，上述最优控制问题可转化为时变线性二次型问题，即同时考虑状态变量与控制变量的二次型性能指标函数为

(2)

基于极小值原理[25]，采用哈密顿函数确定最优控制问题。最优条件为

U(t)BT(t)λ*(t)≥U*(t)BT(t)λ*(t)

(3)

其中：λ*(t)为共态变量。

若区间[0,tf]内不存在函数λ*(t)B(t)=0的子区间，则对于最优控制问题，可寻求m维有界闭集中的最优控制u*(t)，满足不等式约束

|Ui(t)|≤U

(4)

应用极小值原理，最优控制问题可转化为时间最优控制问题，即bang-bang控制函数为

U*(t) = -Usign(BT(t)λ*(t))

(5)

同时可得极值必要条件及边界条件为

根据式(5)～(7)，求得最优控制力∓U。bang-bang控制的优点在于可直接使用被要求的最大控制力，可能会对振动响应产生较好的控制效果。

当控制变量受Umin≤U≤Umax约束时，可使性能指标(2)达到最小控制力的表达式为

(8)

若控制变量无约束，与哈密顿函数相联系的线性系统(1)关于控制变量逐点可微，最优条件为

(9)

1.2 线性二次型调节器(LQR算法)

当控制变量满足二次型性能指标(2)且无约束条件时，控制力在状态变量Z(t)中为线性的

U(t)=-G(t)Z(t)=-R-1BTP(t)Z(t)

(10)

矩阵P(t)可通过黎卡提方程获得

(11)

给定边界条件为P(tf)=S。该方法的优点允许控制通过状态反馈函数表示，并将系统从开环控制系统转向闭环控制系统。状态系统空间方程(8)可表示为

(12)

其中:F(t)包含了输入扰动或外部作用力。

黎卡提方程可进行离线求解。采用该方法可考虑时变模态力，并计算随时间变化的状态变量Z(t)。

若控制变量U(t)受不等式|U(t)|≤U约束时，式(8)中λ(t)=P(t)Z(t)，进而基于LQR算法求解具有控制变量约束的状态空间方程。

1.3 状态相关的黎卡提方程

状态相关的黎卡提方程是一种在线计算控制函数的方法[19]，可应用在拟线性形式下的非线性系统

式(13)通过状态反馈控制法则确定，每一时间步ti的控制函数为

U(ti)=-G(ti)Z(t)=-R-1BT(ti)P(ti)Z(t) (14)

P(ti)可通过状态相关的黎卡提方程在每一时间步ti上求解并不断在线更新

PA(ti)+A(ti)TP-PB(ti)R-1BT(ti)P+Q=0

(15)

2 移动质量-梁系统的最优振动控制

考虑移动质量-梁系统的最优振动控制问题时，系统的动力相互作用可在模态坐标中进行，其中动力系统为时变系统。应用以往时不变控制方法将会得到次优化控制效果，尽管控制效果有所提高。该情况下采用适当的性能指标合成时变最优方案体现出一定的优势，可让控制工程师了解何种方案接近最优。文中给定终端时间tf=L/v，提出解决时变最优控制问题的方案。外部激励函数与移动质量m和移动速度v相关，通过状态空间方程体现。

2.1 移动质量-梁耦合系统的运动微分方程

假设任意时间t内(t∈[0,tf])有一移动质量m以恒等速度v在长度为L的梁上从左至右运行。假定无接触耗损，采用欧拉-伯努利理论获得耦合系统的运动微分方程为

(16)

其中:EI为梁的抗弯刚度；ρ为梁的单位长度质量密度；A为梁的截面面积；δ为Dirac函数；g为重力加速度；c为阻尼系数。

选取梁的振型函数作为模态函数，采用模态叠加法对式(16)进行坐标变换，变换形式为

w(x,t)=ΦT(x)q(t)

(17)

其中：Φ(x)为模态形状函数向量；q(t)为模态坐标向量。

将式(17)代入式(16)进行模态展开，将得到的等式两端分别乘以Φ(x)并沿0到L积分，最终的微分方程写成矩阵形式为

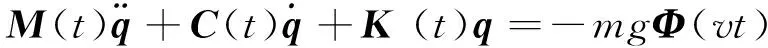
(18)

式(18)表示具有时变矩阵系数的一种动力耦合系统。其中:M(t)=M+ΔM(t)；C(t)=C+ΔC(t)；K(t)=K+ΔK(t);假定t≤0时系统是静止的。

M,C和K为时不变矩阵，分别定义为

时变矩阵系数ΔM(t)，ΔC(t)及ΔK(t)分别为

当移动质量离开梁末端时，即t>tf，梁作自由振动，其动力系统方程为

(21)

2.2 移动质量-梁耦合系统的最优控制问题

移动质量作用下梁的最优振动控制问题可划分为两个子问题：a.当质量在梁上移动时，控制问题为一时变最优问题，用给定的终端时间确定，并采用最优控制方法；b.当质量离开梁末端时，控制问题为一自由振动的时不变最优控制问题，亦可采用LQR算法等控制方法解决该类问题。笔者给出的控制目标为移动质量作用下梁的中跨挠度最小值。若将k个控制器安装在梁上指定的坐标位置xr1,xr2,…,xrk，给定t≤tf条件的受控系统动力方程为

(22)

其中：Φ(xri)Ui可对式(22)起控制作用。

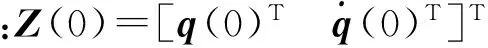
时变矩阵B(t)与作动器的位置相关，不仅影响设计过程，同时对系统的可控性产生一定的影响。此外，对挠度响应的控制需权重矩阵Q和R，Q和R的选取有时会影响控制力U(t)，从而影响对振动的控制效果。当控制准则确定，移动质量问题的另一特殊性可以考虑激振力mgΦ(vt)，则式(23)可增广为

3 数值算例

为评估二次型性能指标及其对结构最优问题的适用性，将最优控制方法应用在恒速状态移动质量作用的单跨简支梁上，通过理论验证是否可使挠度响应最小化。车-桥系统及弹-炮系统等均可简化为移动质量-梁模型[13-14,26]。几何尺寸和动力特征为：梁跨度L=1 m，抗弯刚度EI=3.68 Nm2,单位长度质量ρA=0.22 kg/m，阻尼系数c=1.6,移动质量m=0.5 kg，恒速v=2 m/s，恒定的终端时刻tf=0.5 s,如图1所示。对于笔者给出的单跨简支梁，其第i阶模态为

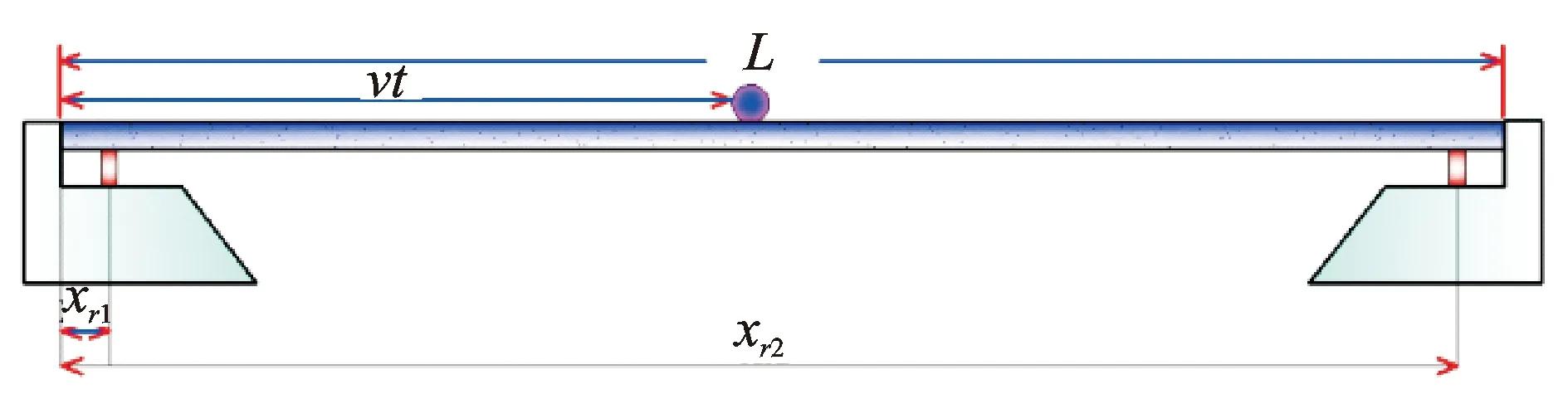
图1 具有作动器的单跨简支梁(安装在梁的两端xr1和xr2)Fig.1 A single span simply supported beam with two actuators positioned on both sides of the beam at locations xr1 and xr2

(25)

以下分析取简支梁的前两阶模态计算梁的中跨挠度，并通过挠度时程曲线的减小幅度评估不同控制方法的控制效果。例如，采用不同水平的控制力Ui(t)降低同阶内的挠度振幅，若控制力绝对水平相对较低，则相应的设计方法应予以考虑。

3.1 恒速状态移动质量作用的柔性梁振动响应

当移动质量以恒等速度在梁上运行时，可通过式(18)求解梁中跨挠度响应，此时为时变动力响应问题。当移动质量离开梁后(t>tf)，梁作自由振动，由式(21)可求解时不变动力响应问题。文中柔性梁的一阶固有频率为40 rad/s，二阶、三阶与四阶频率分别为160,360和640 rad/s。图2为移动质量作用在梁上和离开梁后的中跨挠度响应时程曲线。可以看出，超过前两阶模态不足以增加柔性梁挠度响应的精度，取一阶和二阶模态时，梁的挠度响应基本一致，从而验证了笔者取前两阶模态的合理性。图2显示终端时刻tf=0.5 s，当t≤tf时，即移动质量作用在梁上时可使梁产生最大挠度响应振幅为0.096 cm，当超过终端时刻tf时，即移动质量离开梁后，依然存在自由振动，最大响应振幅不断衰减。

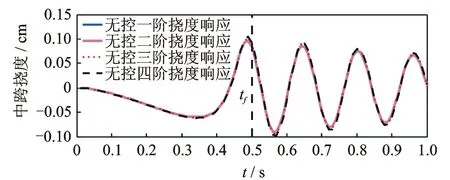
图2 无控状态下的梁中跨挠度响应Fig.2 Mid-span deflection of the beam at uncontrolled condition

3.2 无约束的控制变量

应用所提控制方法求解式(22)在给定t≤tf条件时的挠度响应；当t>tf时梁作自由振动，可采用基于线性二次型控制问题的控制函数求解时不变部分。控制函数u(t)=-GZ(t)，恒定增益控制矩阵G可通过时不变矩阵系数得到

通过式(26)控制梁自由振动时的挠度响应，梁自由振动时刻为tf～2L/v。将两个作动器分别安装在梁上指定位置xr1=0.16 m和xr2=0.78 m，如图1所示，笔者考虑所设控制器对梁中跨位置x=L/2时的挠度响应产生影响。根据实际建造的必要性，两作动器有时可安装在梁的同一端xr1=0.10 m和xr2=0.153m或梁末端xr1=0.70 m和xr2=0.81 m处。

定义二次型性能指标中的误差和控制权重矩阵Q=diag(1 000,100,10,10) 和R=diag(0.9,0.9)，计算恒定增益控制矩阵G(xr1,xr2)，采用时不变线性二次型公式求解式(22)。对于时变系统，增益矩阵G(xr1,xr2,t)=-R-1BT(xr1,xr2)P(t)具有时变性，可以反解黎卡提方程求解P(t)。此外，求解P(t)时给定的边界条件P(tf)=S可采用李雅普诺夫方程获得。图3为基于时不变线性二次型控制和无控系统的中跨挠度响应时程曲线，设计的控制器在梁上指定的位置xr1=0.16 m和xr2=0.78 m。可以看出，当移动质量作用在梁上时，采用时不变控制对梁挠度响应进行控制后的最大响应振幅为0.040 5 cm，控制效果为57.81%；移动质量离开梁后作自由振动时的响应控制效果依然显著。以上结果表明，时不变控制方法对梁挠度响应的抑制具有一定的效果。

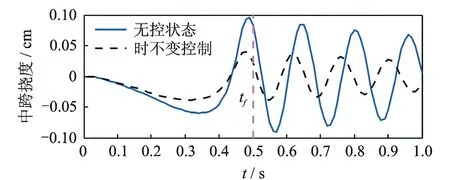
图3 时不变控制与无控状态下的中跨挠度Fig.3 Mid-span deflection of the beam under time- invariant control and uncontrolled condition

图4为不考虑移动质量的时变控制、考虑移动质量的时变控制与时不变控制方法获得的中跨挠度曲线。可以看出：采用式(23)的时变控制方法得到的挠度振幅峰值为0.036 3 cm，控制效果为62.19%；采用时不变控制方法得到的挠度振幅峰值为0.040 5 cm，控制效果为57.81%；采用式(24)的时变控制方法得到的挠度振幅峰值为0.020 6 cm，控制效果为78.54%。结果表明：当作动器在梁的两端时，时变控制方法的整体优势不明显；采用考虑移动质量的时变控制方法可以使控制目标效果最佳，此时该最优方案关于性能指标是最优的。

图4 未考虑移动质量时变控制、考虑移动质量时变控制与时不变控制下的中跨挠度Fig.4 Mid-span deflection of the beam under time-dependent control without considering moving mass, time-dependent control with considering moving and time-invariant control

此外，控制权重系数矩阵R对时变控制方法的控制效果起一定的影响作用。图5为权重矩阵R不同时的梁中跨挠度响应。从图5看出，相对控制权重系数取R=diag(0.9,0.9)时，控制权重系数矩阵取R=diag(9,9)会降低控制效果。结果表明：为考虑控制器的作用效果，权重系数R的取值应在适当范围内足够小。

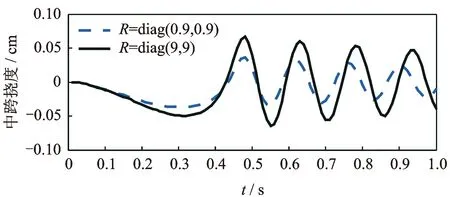
图5 权重矩阵R不同时的梁中跨挠度响应Fig.5 Mid-span deflection of the beam for different R

若两作动器有时需要安装在梁的同一侧，时不变增益控制器G(xr1,xr2)与时变增益控制器G(xr1,xr2,t)之间的差异变得更加重要，系统与时间相关的特性不可忽略，如图6所示。图6(a)为作动器全部安装在梁左侧时不同最优控制方法获得的控制效果。图6(b)为作动器均安装在右侧时不同控制方法获得的控制效果。可以看出，同时安装在右侧的控制器能够使控制目标性能最佳，而考虑移动质量的时变最优控制方案无疑是最佳的。限于篇幅要求，表1仅给出作动器位置对时变控制方法(考虑激振力)的影响。可以看出，若考虑实际建造的必要性，作动器同时放在右侧位置，控制效果为最佳且作动器出力绝对水平相对稳定。

采用SDRE求解时变增益控制器G(xr1,xr2,t)时，需对矩阵P(ti)实时在线更新。图7为SDRE控制与考虑移动质量(激振力)的时变控制获得的中跨挠度曲线。可以看出，SDRE可以使受控系统的最大振幅响应达到最佳控制效果，相比考虑移动质量的时变控制方案，该方案性能指标最优。作动器位置一定时(xr1=0.16,xr2=0.78)，各种控制方法的控制力U1和控制力U2在0～0.5 s内的时程曲线如图8所示。

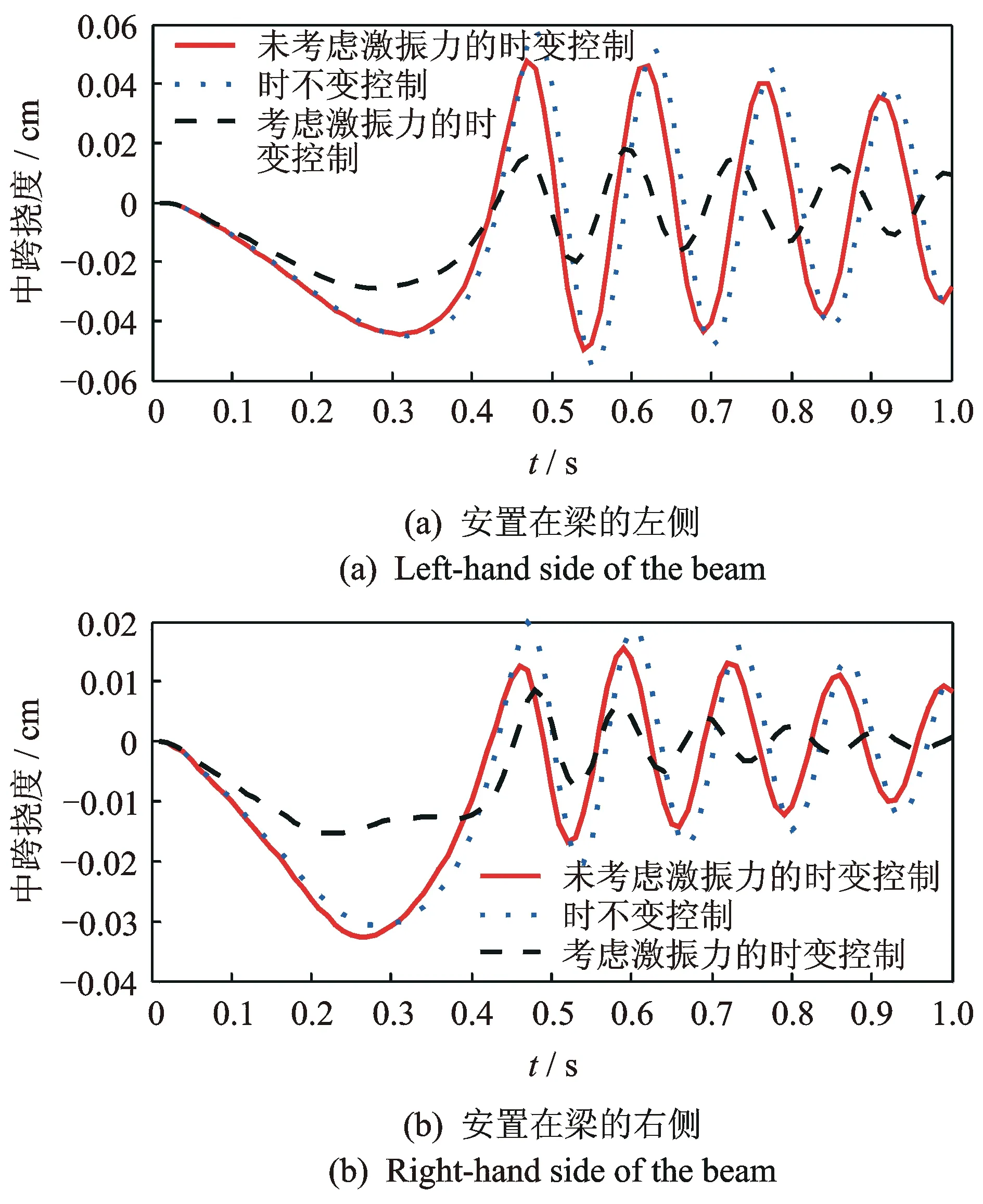
图6 两作动器安装位置Fig.6 Two actuators position

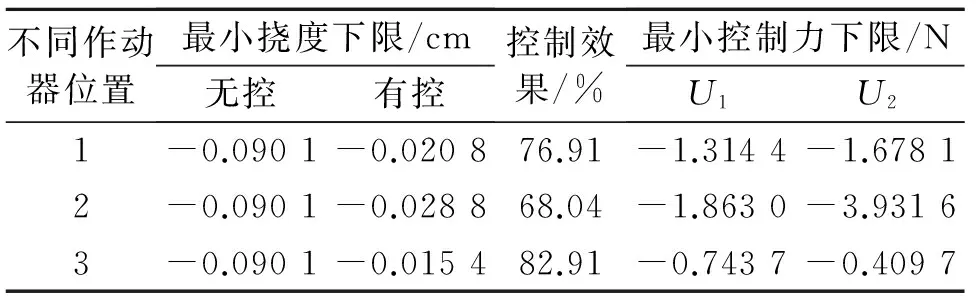
不同作动器位置最小挠度下限/cm无控有控控制效果/%最小控制力下限/NU1U21-0.0901-0.020876.91-1.3144-1.67812-0.0901-0.028868.04-1.8630-3.93163-0.0901-0.015482.91-0.7437-0.4097

1:xr1=0.16，xr2=0.78;2:xr1=0.1，xr2=0.153;3:xr1=0.7，xr2=0.81

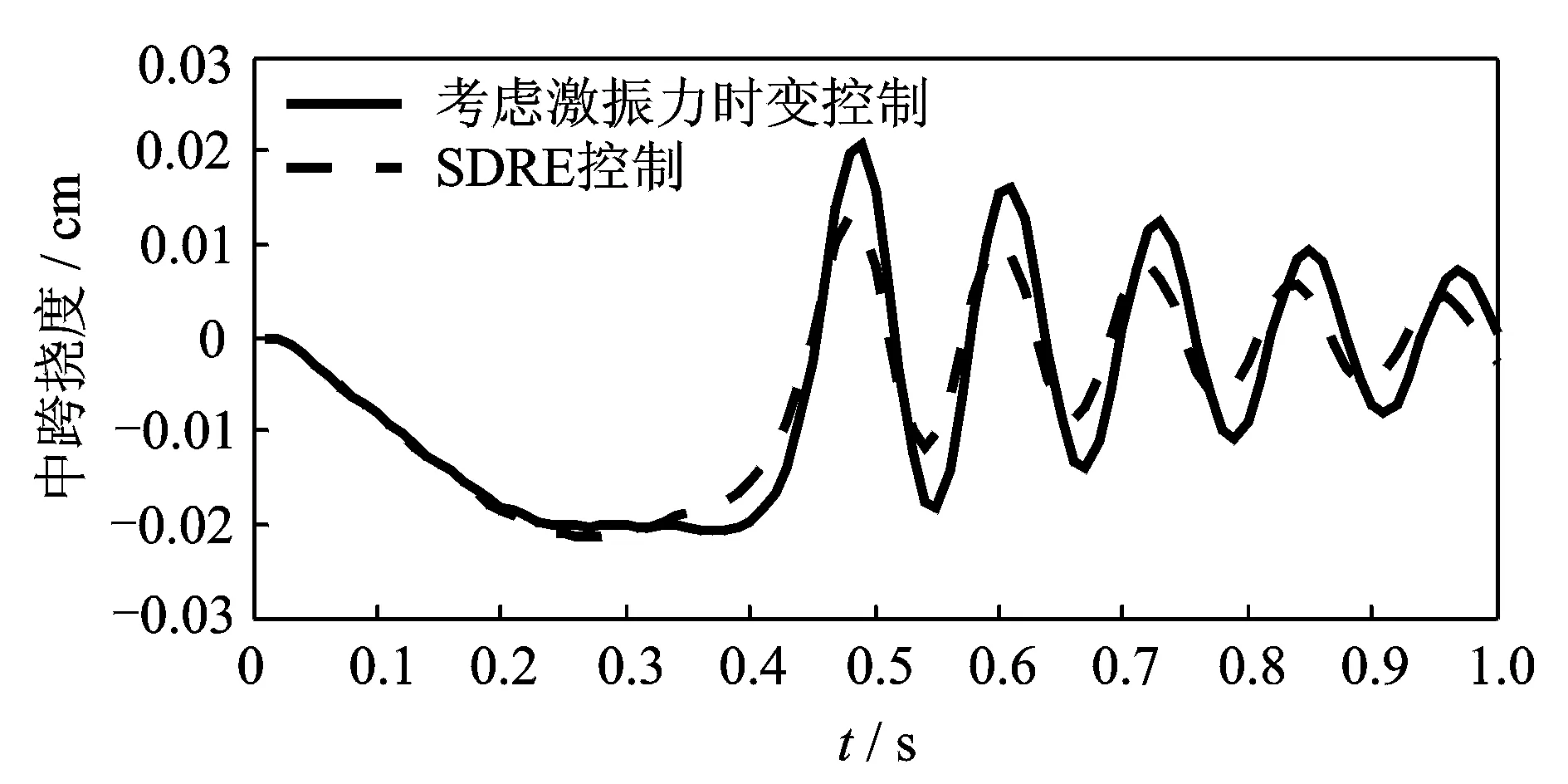
图7 考虑激振力的时变控制与SDRE控制的中跨挠度响应Fig.7 Time-dependent with considering moving force and SDRE control for mid-span deflection

图8 不同控制方法Fig.8 Control forces of different control methods

3.3 具有约束的控制变量

数值分析结果均基于控制力无约束情况下获得，从数学角度看，无约束条件可使关于控制变量的哈密顿函数逐点可微并允许黎卡提方程的使用，从而对系统产生反馈控制。由于现有作动解决方案的局限性，实际情况下需要对控制作用施加边界约束条件。根据控制力最大上限振幅约为2 N(只考虑作动器安装在梁两端的情况)，这里寻求一种控制力约束条件，达到类似的控制效果。首先，根据提出的bang-bang控制方法，给出控制变量的约束条件|Ui(t)|<1.1；其次，基于式(2)，采用含有边界约束控制力的式(8)计算。上述最优控制方法需要解决两点边值问题，式(5)的不连续性使式(1)和(6)雅克比矩阵为非凡的。图9(a)为控制力约束条件|Ui(t)|<1.1时，bang-bang控制方法和无控下的挠度时程曲线。可以看出，边界控制依然具有良好的控制效果。此外，从挠度振幅峰值下限的控制效果角度出发，基于增广矩阵的LQR边界控制方法的控制效果为77.25%，基于bang-bang控制方法的控制效果为77.47%，两种最优方法的控制效果相近，但若是在梁的自由振动阶段，基于增广矩阵的LQR边界控制效果优于bang-bang控制的控制效果，如图9(b)所示。由此可知：考虑到实际作动器设备存在局限性，控制工程师选取基于增广的边界控制方案可达到最佳控制效果。值得注意的是，边界控制方法中的共态变量λ(t)需要进行离线计算后代入系统，但获得的系统为开环控制系统。作动器位置一定时(xr1=0.16,xr2=0.78)，这两种控制方法的控制力U1和U2在0～0.5 s内的时程曲线如图10所示。不同控制方法的控制效果、最大控制力上限和挠度峰值下限如表2所示。

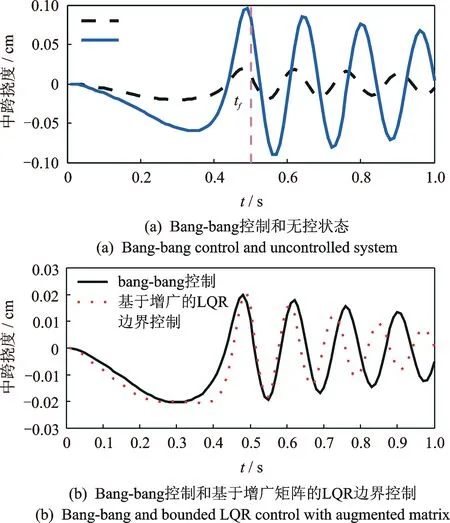
图9 中跨挠度响应Fig.9 Mid-span deflection

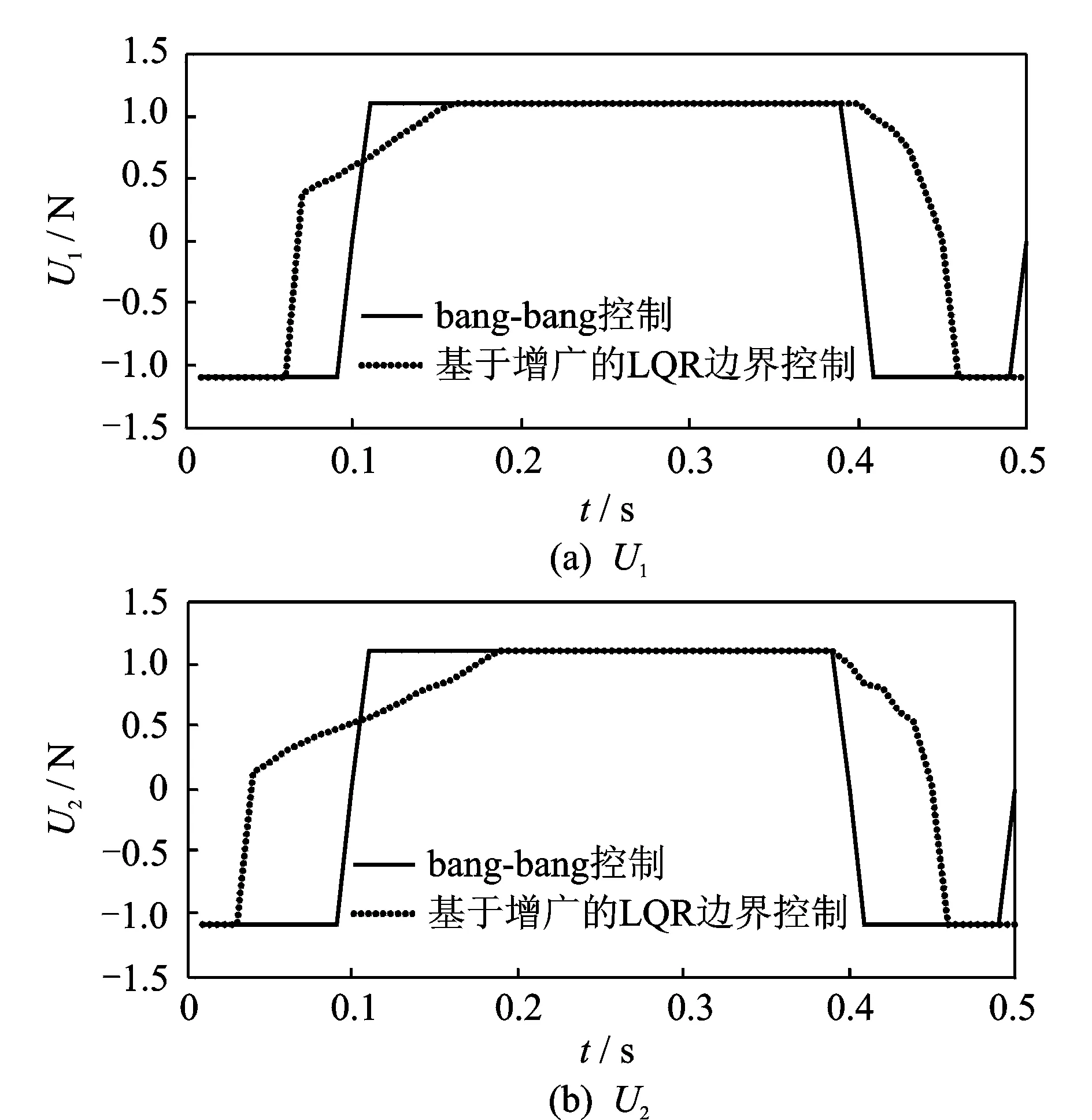
图10 Bang-bang控制和基于增广矩阵的LQR边界控制Fig.10 Control forces of bang-bang and bounded LQR control with augmented matrix

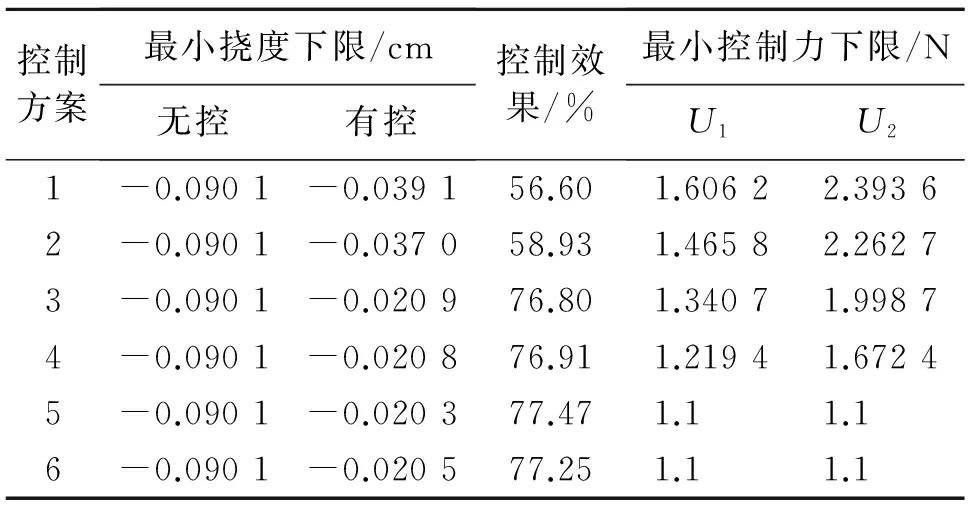
控制方案最小挠度下限/cm无控有控控制效果/%最小控制力下限/NU1U21-0.0901-0.039156.601.60622.39362-0.0901-0.037058.931.46582.26273-0.0901-0.020976.801.34071.99874-0.0901-0.020876.911.21941.67245-0.0901-0.020377.471.11.16-0.0901-0.020577.251.11.1

1为时不变控制;2为无增广时变控制;3为有增广时变控制;4为SDRE控制;5为bang-bang控制;6为有增广LQR边界控制

4 结束语

基于一般基础性的移动-载荷问题，研究了恒速状态移动质量作用的柔性梁最优振动控制问题。基于状态变量和控制变量的线性二次型性能指标，给出线性时变系统的状态空间方程。将最优控制问题划分为时变与时不变最优问题，根据实际要求，通过数值模拟比较多种最优控制方法的优缺性。对于特定的作动器位置，应当考虑采用具有时变特征的控制方法替代时不变控制方法。SDRE求解时变增益矩阵G(xr1,xr2,t)时，可随着时间步ti不断对矩阵P(ti)更新，与时变控制方法相比，SDRE控制方案的性能指标最优。文中较为复杂的边界最优控制问题需要系统为开环系统，给定控制变量不等式约束条件，考虑两点边界值问题，采用黎卡提方程求解时变系统矩阵。结果表明：梁作自由振动时，基于增广的LQR边界控制效果优于bang-bang控制，从实际角度出发，前者方案不仅关于性能指标最优，也是控制工程师感兴趣的最佳控制方法。

[1] Alkhatib R, Golnaraghi M F. Active vibration control: a review[J]. The Shock and Vibration Digest, 2003,35:367-383.

[2] Preumont A. Vibration control of active structures, dordrecht[M]. 2nd ed. The Netherlands: Kluwer Academic Publishers, 2006.

[3] Tatavolu V R, Panchumarthy S R. Embedded computer based active vibration control system for vibration reduction of flexible structures[J]. Journal of Computer Science, 2013,9:838-846.

[4] Inman D J. Modal control for smart structures[J]. Mathematical, Physical and Engineering Sciences, 2001,359:205-219.

[5] Abdel-Rohman M, Quintana V H, Leipholz H H. Optimal control of civil engineering structures[J].Journal of the Engineering Mechanics Division, 1980,106:57-73.

[6] Ram Y M, Mottershead J E. Receptance method in active vibration control[J]. AIAA Journal, 2007,45:562-567.

[7] Ouyang H. Pole assignment of friction-induced vibration for stabilization through state-feedback control[J]. Journal of Sound and Vibration, 2010,329(11):1985-1991.

[8] Liu J, Qu W L, Pi Y L. Active/robust control of longitudinal vibration response of floating-type cablestayed bridge induced by train braking and vertical moving loads[J]. Journal of Vibration and Control, 2010,16:801-825.

[9] Deng F, Remond D, Gaudiller L. Modal control using real-time identification for time-varying structures[J]. Mecanique & Industries, 2010,11:513-520.

[10]Wu Z, Soong T T. Modified bang-bang control law for structural control implementation[J]. Journal of Engineering Mechanics, 1996,122:771-777.

[11]Kim J H, Clark W W, Marangoni R D. A comparison of reaction force suppression to displacement suppression for vibration control in a flexible structure[J]. Journal of Sound and Vibration, 1997,208:225-242.

[12]Shamma J, Xiong D. Linear nonquadratic optimal control[J]. IEEE Transactions on Automatic Control, 1997,42:875-879.

[13]王颖泽，张小兵. 变速多移动质量耦合作用下柔性梁系统振动响应分析[J]. 振动与冲击,2011,30(8): 56-66.

Wang Yinze, Zhang Xiaobing. Vibration analysis of flexible beam under the action of multi-moving masses with variable speeds[J]. Journal of Vibration and Shock, 2011,30(8):56-66. (in Chinese)

[14]彭献，刘子建，洪家旺. 匀变速移动质量与简支梁耦合系统的振动分析[J]. 工程力学,2006,23(6):25-29.

Peng Xian, Liu Zijian, Hong Jiawang. Vibration analysis of a simply supported beam under moving mass with uniformly variable speeds[J]. Engineering Mechanics, 2006,23(6):25-29. (in Chinese)

[15]Pierson H, Brevick J, Hubbard K. The effect of discrete damping on the traverse vibration of beams[J]. Journal of Sound and Vibration, 2013,332:4045-4053.

[16]Raftoyiannis I G ,Michaltsos G T. Mathematical modelling for seismic response of steel bridges with internal damping systems[J]. Journal of Vibration and Control, 2012,19:687-707.

[17]Ouyang H. Moving-load dynamic problems: a tutorial[J]. Mechanical Systems and Signal Processing, 2011,25:2039-2060.

[18]Sung Y G. Modelling and control with piezoactuators for a simply supported beam under moving mass[J]. Journal of Sound and Vibration, 2002,250:617-626

[19]Nikkhoo A, Rofooei F R, Shadnam M R. Dynamic behavior and modal control of beams under moving loads[J]. Journal of Sound and Vibration, 2007,306(3):712-724.

[20]Zarfam R, Khaloo A R. Vibration control of beams on elastic foundation under a moving vehicle and random lateral excitations[J]. Journal of Sound and Vibration, 2012,331:1217-1232.

[21]Xiong Y P, Xing J T, Price W G. An active control method using power flow for vehicle-bridge interaction systems[C]∥Proceedings of the ASIA-Pacific Vibration Conference. Singapore: [s.n.], 1999:13-15.

[22]Mofid M, Eftekhar A S, Afghani K R. Dynamic control of beams acted by multiple moving masses in resonance state using piezo-ceramic actuators[J]. Proceedings of the SPIE: Active and Passive Smart Structures and Integrated Systems,2012:8341.

[23]Naidu D S. Optimal control systems[M]. Boca Raton, FL: CRC Press, 2003.

[24]Kamien M I, Schwartz N L. Dynamic optimization: the calculus of variations and optimal control in economics and management[M]. Amsterdam, North-Holland: Elsevier, 1991.

[25]吴受章.最优控制理论与应用[M].北京：机械工业出版社,2008:112-151.

[26]马志赛，刘莉，周思达. 移动质量简支梁耦合时变系统建模与实验设计[J]. 振动、测试与诊断, 2015, 35(5): 913-920.

Ma Zhisai, Liu Li, Zhou Sida. Modeling and experimental design of the couple moving-mass and simply supported beam time-varying system[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(5):913-920. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.01.020

*航空科学基金资助项目(2013ZB08001)；国家自然科学基金资助项目(11272257);陕西省自然科学基金资助项目(2014JM6220)；西北工业大学研究生创意创新种子基金资助项目(Z2015084)

2015-10-04；

2016-01-11

TH113; O32; O302

刘骁骁，男，1989年12月生，博士生。主要研究方向为复杂结构抗震减震及系统确定和不确定性振动控制。曾发表《基于β-二项分布的结构易损性分析》(《计算力学学报》2014年第31卷第6期)等论文。 E-mail: xxliu1989@163.com 通信作者简介：任兴民，男，1960年10生，教授、博士生导师。主要研究方向为转子动力学、航空发动机振动及振动主动控制。 E-mail: renxmin@nwpu.edu.cn