基于小波理论和ARIMA—EGARCH模型的农产品短期价格预测

2017-03-15闪利平刘世江

中国市场 2017年5期

闪利平+刘世江

[摘要]文章以玉米为代表研究了农产品的价格趋势。选用2014年1月到2015年12月河南的玉米价格数据，用db4小波对原始数据进行去噪处理后，通过ARIMA-EGARCH模型对短期内玉米价格进行了预测，得出短期内玉米价格会进一步下降的结论。进一步，对比分析了ARIMA模型和ARIMA-EGARCH模型预测结果，证明ARIMA-EGARCH复合模型的预测精度更高。基于持续下降的价格趋势，政府应尽快采取措施以保障农产品价格的稳定。

[关键词]小波分析；时间序列；ARIMA模型；EGARCH模型

[DOI]1013939/jcnkizgsc201705030

1引言

我国是农业大国，农产品价格稳定是人民群众正常生活的重要前提。近年来政府在农产品方面给出多项补贴政策，但是玉米供给量逐年增加，政府收购的力度明显下降，农产品价格起伏较大。农产品作为农民收入的主要经济来源，价格大幅度下降将严重影响农民的生活和种植的积极性。农产品作为基础商品，价格波动直接影响后续产业。因此准确预测农产品价格走势对农业及其相关产业具有重要意义。

本文通过小波理论对原始数据进行去噪处理后建立ARIMA-EGARCH模型，以期能更准确地预测玉米的价格走势，为政府制定农产品方面的政策提供参考，同时对农产品期货市场上的投资者也具有指导意义。

2传统的价格预测模型和波动率模型

21传统的价格预测模型及其应用

针对农产品价格，诸多学者进行了深入广泛的研究。王勇、张浩[1]用马尔可夫模型对小麦的期货价格进行预测，结果表明从长期来看硬麦的期货价格极大可能处于高位区。刘峰、王儒敬[2]用ARMA模型预测白菜的价格。程贤禄[3]用马尔可夫链法对北京市蔬菜价格进行预测，结果表明建立的蔬菜价格预报体系可以对实际蔬菜价格进行预测。刘海清、方佳[4]运用指数平滑模型对海南省芒果价格进行长期预测，实验表明该模型能对芒果价格曲线进行很好的拟合。但是价格除了有趋势性还有波动性，上述模型对价格的趋势性进行很好的预测但缺乏对于价格波动率的描述。

22波动率模型及其应用

1986年Bolloerselev提出了广义自回归条件异方差模型，即GARCH模型。GARCH（p，q）模型定义如下：

GARCH模型自产生以来，很多学者不断地探索研究，在此模型基础上提出更能反映市场情况的模型，例如MGARCH模型、EGARCH模型等。近年来GARCH模型在金融领域已经得到广泛的应用。杨夫立[5]运用GARCH 模型计算收益率在正态、学生t和广义误差（GED）分布下的基金市场风险，研究表明基于GED分布的 GARCH 模型计算的 VAR 值最能真实地反映基金风险。肖云湘、李星野[6]结合多项式回归和GARCH模型对中国外汇储备进行预测。夏冰[7]研究通过ARCH类模型对农产品价格波动集聚性进行对比分析，证实部分农产品价格在1%波动水平时呈现出高阶ARCH效应。万蔚、江孝感[8]运用GARCH模型、TARCH 模型和 EGARCH 模型对上证综合指数和深圳成分指数进行拟合，结果显示EGACH 模型能更有效拟合股市的波动性。高辉、赵进文[9]运用GARCH模型研究发现，上海和伦敦两市期货收益率的波动性存在非对称性、溢出效应、杠杆效应。由上述可知，GARCH模型能够很好地描述时间序列的波动性，这一点已经被学者广泛认可。

综上所述，本文在运用模型分析短期内的价格时，考虑到价格的趋势性和波动性，将结合ARMA模型和GARCH模型对玉米价格分析预测。这就解决了ARMA模型仅从价格趋势性的角度和EGARCH模型僅从趋势性方面来分析玉米价格的不全面问题。

23小波理论

小波函数是在传统傅里叶函数上发展而来的，小波变换[6]是通过平移和伸缩等运算对信号进行多尺度细化分析，利用多分辨率分析来得到更多的信息。当满足如下完全重条件则称为基小波。

小波本身具有多分辨分析和良好的非线性局部逼近功能等多种特性，能够对研究对象进行更为细致的逼近，因此小波分析又被人们称为“数学显微镜”。近年来逐渐被引入经济领域，并得到广泛的应用。基于小波的优势和上述模型，文章的建模结构是：第一步，对原始数据进行小波分解，并确定要选用的层数和数据；第二步，对选取的主要趋势数据运用ARIMA模型进行拟合，并对未来价格进行第一次预测；第三步，对残差部分进行高阶ARCH检验，若存在高阶ARCH效应则进一步建立GARCH模型并进行第二次预测。反之在第二步处结束。详见下图。

3实证分析

31数据来源

本文选用的模型是短期预测模型，由于玉米价格受政策因素影响比较明显，所以为了提高预测进度，笔者选用的数据是在统一政策时期的数据。本文以2014年1月到2015年12月的玉米价格为研究对象，用小波对数据分解，经尝试，第一层可以代表原始数据的大部分信息，所以选取第一层的主要趋势进行建模，从而分析得到预测。

32平稳性检验

从上图可以看出数据具有明显的下降趋势，初步判断序列不平稳。对数据进行ADF检验，数据不平稳，对数据进行平稳化处理，数据进行一次差分后变得平稳。由ADF检验结果可知，-5639824小于1%、5%、10%显著性水平下的临界值，p值趋近于 0，根据ADF 检验原理序列是平稳的，因此ADF检验通过，即数据经过一阶差分后变平稳。

33模型参数估计及模型定阶

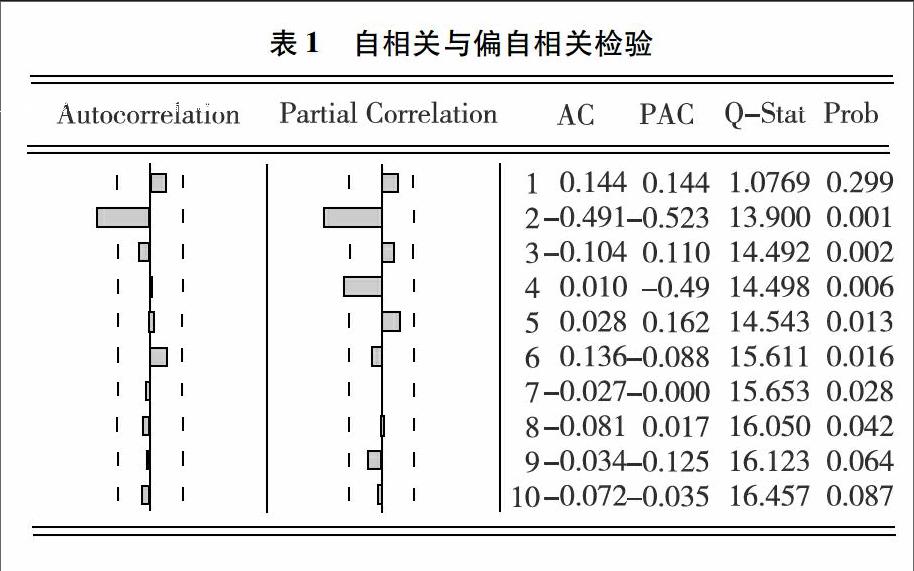
利用自相关与偏自相关函数和 Q 统计量来检验序列相关性，序列自相关和偏自相关图如下表所示，Q统计量对应的p值趋近于 0，进行差分后的序列的自相关系数和偏自相关系数如表1所示。

由自相关和偏自相关图可知，p可以选择1或者2，q可以选择1或者2，由于一阶差分，所以d=1，从而得到ARIMA（1，1，1）、ARIMA（1，2，1）、ARIMA（2，1，1）、ARIMA（2，2，1）。通过尝试对比四个模型调整后的可抉系数同时考虑AIC最小准则，最终ARIMA（2，2，1）模型比较好。模型参数估计及检验结果见表2。

34模型检验

由上述结果可知，ARIMA（2，2，1）是选择的最佳预测模型，参数估计结果如上表所示。为提高模型的精度，对拟合过后的残差部分进行高阶ARCH效应检验，结果表明残差项存在高阶ARCH效应，进一步建模增加模型的精度。EGARCH模型检验结果如表3所示。

35结果分析

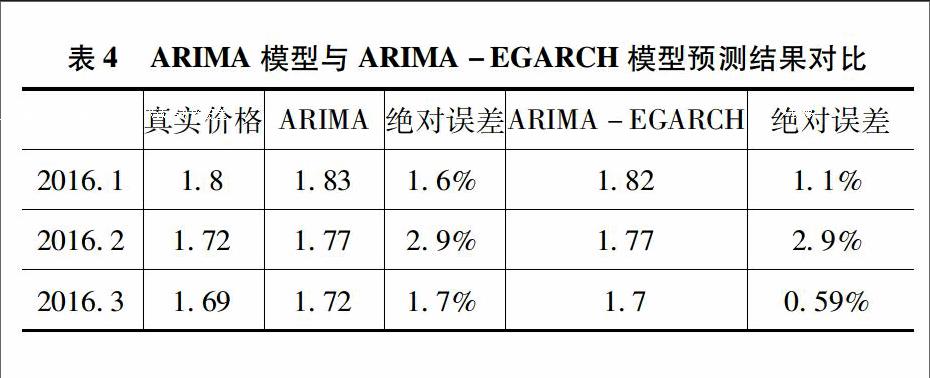
将ARIMA-EGARCH模型预测出的数据与原始的数据进行对比分析（见表4），基于小波分解的ARMA-EGARCH模型预测出的数据与原始数据之间的绝对误差很小，回归函数的标准误差在04以内，对比只用ARIMA模型进行预测的结果，可以判断该混合模型的预测精度较高。

4结论

本文研究农产品价格问题，以玉米价格为例进行研究，通过建立计量模型进行分析预测，得出以下结论：第一，与传统预测模型相比，基于小波理论的ARMIA-EGARCH复合模型在预测方面更为精确；第二，当前政府政策不变的情况下，短期内玉米价格会进一步下降，不过下降幅度较小。

综上所述，基于小波理论的ARIMA-GARCH模型有着预测精度高的优势，根据具体情况可以考虑将模型运用到其他领域进行预测。基于农产品价格持续下降的趋势，政府可以考虑通过对玉米储备进行调整从而引导市场的供需及出口状况，防止大规模囤积、卖空等情况的出现，稳定农产品价格水平。

参考文献：

[1]王勇，张浩小麦期货价格预测的马尔可夫模型[J].安徽农业科学，2008，36（5）：1721

[2]刘峰，王儒敬，李传席ARMA模型在农产品价格预测中的应用[J].计算机工程与应用，2009，45（25）：238-248

[3]程贤禄北京市农产品批发市场蔬菜价格预测预报体系研究[J].北京农业科学，2002（2）：1-10

[4]刘海清，方佳基于指数平滑模型的海南省芒果价格预测[J].热带东业科学，2010，30（1）：79-81