Fekete-Szegö Problem for Certain Subclass of p-Valent Analytic Functions using Quasi-Subordination

(1.School of Mathematics and Statistics,Chifeng University,Inner Mongolia 024000,China;2.School of Computer and Information Engineering,Chifeng University,Inner Mongolia 024000,China)

§1.Introduction

LetApdenote the class of functions of the form

which are analytic in the unit diskD={z:|z|＜1}.For simplicity,we writeA1=:A.

For two analytic functionsfandg,the functionfis subordinate toginD(see[1]),written as follows

if there exists an analytic functionω,withω(0)=0 and|ω(z)|＜1 such that

In particular,if the functiongis univalent in D,thenf(z)≺g(z)is equivalent tof(0)=g(0)andf(D)⊂g(D).

Ma and Minda[2]introduced and studied the classesS∗(φ)andC(φ)as below

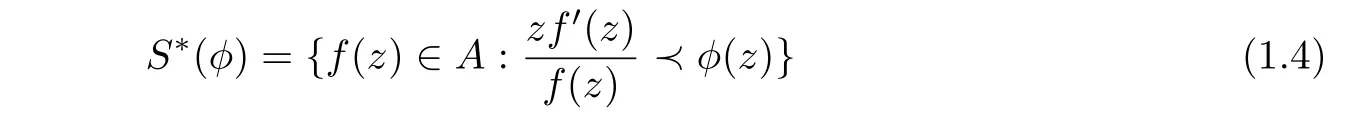
and

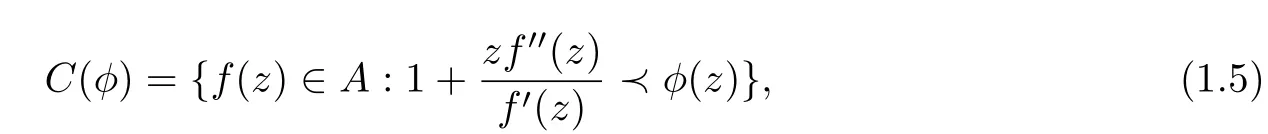
whereφ(z)is an analytic function with positive real part inD,φ(D)is symmetric with respect to the real axis and starlike with respect toφ(0)=1 andφ′(0)＞0.The classS∗(φ)andC(φ)include several well-known subclasses of starlike and convex functions as special case.

In the year 1970,Robertson[3]introduced the concept of quasi-subordination.For two analytic functionsfandg,the functionfis quasi-subordinate toginD,written as follows

if there exist analytic functionsϕandω,with|ϕ(z)|≤1,ω(0)=0 and|ω(z)|＜1 such that

Observe that whenϕ(z)=1,thenf(z)=g(ω(z)),so thatf(z)≺g(z)inD.Also notice that ifω(z)=z,thenf(z)=ϕ(z)g(z)and it is said thatfis majorized bygand writtenf(z)≪g(z)inD.Hence it is obvious that quasi-subordination is a generalization of subordination as well as majorization.See[4-6]for works related to quasi-subordination.

Mohd and Darus[7]introduced the classes(φ)andCq(φ)as below

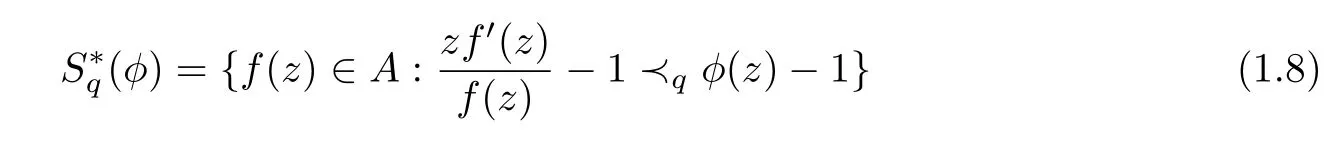
and

The two classes are analogous to the Ma-Minda starlike and convex classes defined in the form of quasi-subordination.

Letf(m)be then-th order ordinary differential operator,for a functionf∈Ap,that is,

wherep＞m,p∈N;n∈N0=N∪{0},z∈D.

Throughout this paper it is assumed that functionφ(z)is analytic inDwithφ(0)=1.Using the operatorf(m),we now de fine the following class ofp-valent analytic functions.

De finition 1.1Let the class(λ,b;φ)consists of functionsf(z)∈Apsatisfying the quasi-subordination

Clearly,we have the following relationship:

It is well known that then-th coefficient of a univalent functionf(z)∈Ais bounded byn(see[8]).The bounds for coefficient give information about various geometric properties of the function.Many authors have also investigated the bounds for the Fekete-Szegö coefficient for various classes[7,9-23].In particular,some authors start to study the Fekete-Szegö problem for various classes using quasi-subordination[7,22,23].In this paper,we obtain coefficient estimates for the functions in the above defined class.

Let Ω be the class of analytic functionsω(z),normalized byω(0)=0,and satisfying the condition|ω(z)|＜1.We need the following lemmas to prove our main results.

Lemma 1.2[24]Ifω∈Ω,then for any complex numbert

The result is sharp for the functionsω(z)=z2orω(z)=z.

Lemma 1.3[2]Ifω∈Ω,then

Whent＜−1 ort＞1,equality holds if and only ifω(z)=zor one of its rotations.If−1＜t＜1,then equality holds if and only ifω(z)=z2or one of its rotations.Equality holds fort=−1 if and only ifω(z)=or one of its rotations while fort=1,equality holds if and only ifω(z)=or one of its rotations.

Also the sharp upper bound above can be improved as follows then−1＜t＜1:

and

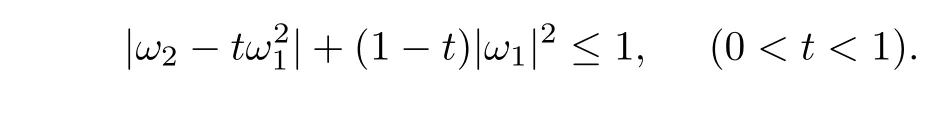
§2.Main Results

Throughout,letf(z)=z+ap+1zp+1+ap+2zp+2+···,φ(z)=1+B1z+B2z2+···,ϕ(z)=c0+c1z+c2z2+···,ω(z)=ω1z+ω2z2+···,B1∈RandB1＞0.

Theorem 2.1Iff(z)∈Apbelongs to(λ,b;φ),then

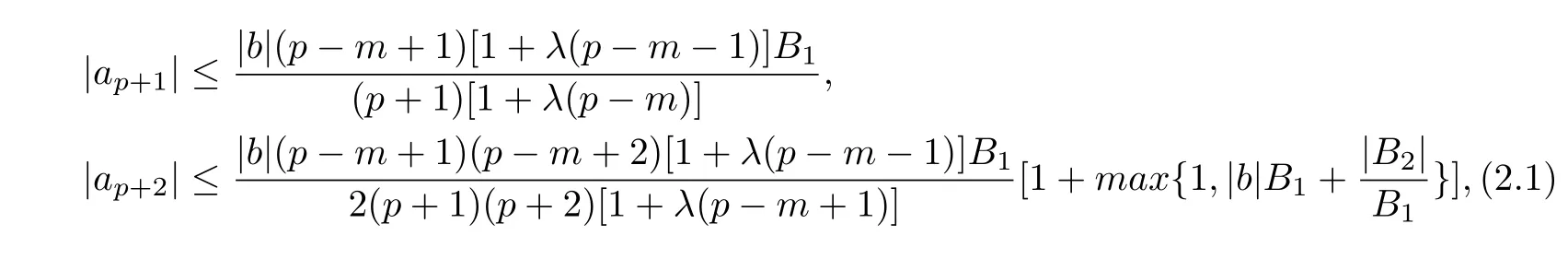
and,for any complex numberµ,

where

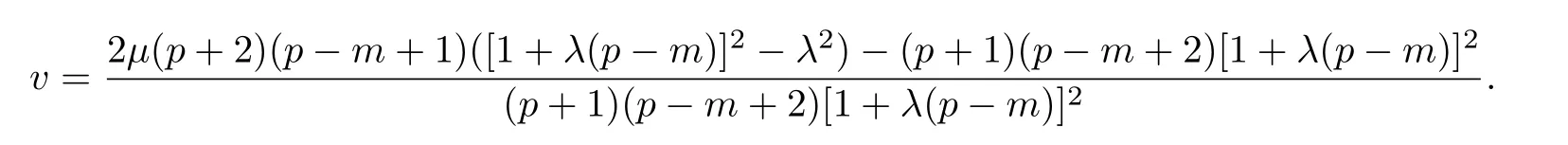
ProofIff(z)(λ,b;φ),then there exist analytic functionsϕ(z)andω(z),with|ϕ(z)|≤1,ω(0)=0 and|ω(z)|＜1 such that

Since

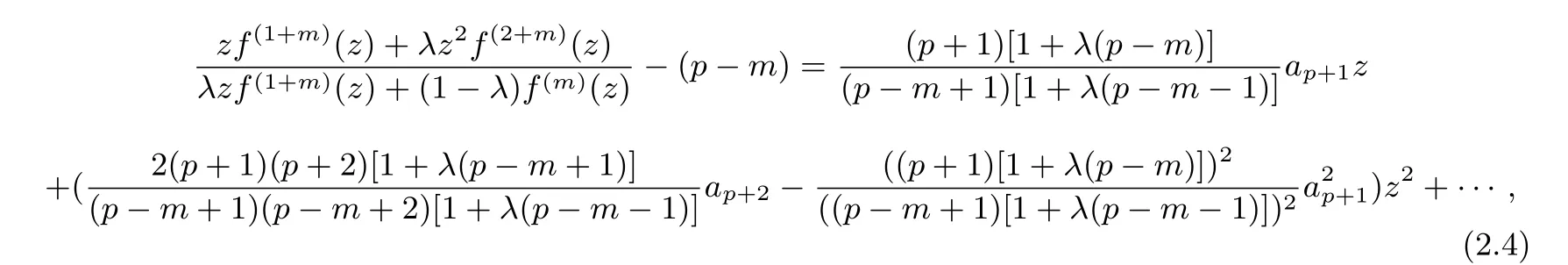
it follows from(2.3)that

Further,

where

Sinceϕ(z)is analytic and bounded inD,we have[25,page 172]

By using this fact and the well-known inequality|ω1|≤1 in(2.6)and(2.7),we get

and

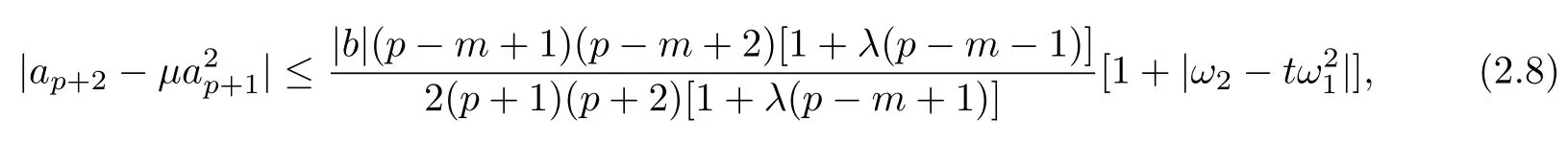
Applying Lemma 1.2 and the triangle inequality to(2.8),we obtain(2.2).The result is sharp for the function

or

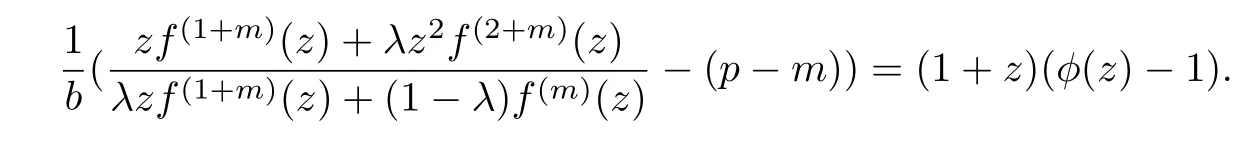
Forµ=0 in(2.2),we have(2.1).The proof of theorem 2.1 is complete.

Corollary 2.2[7]Iff(z)∈Abelongs to(φ),then

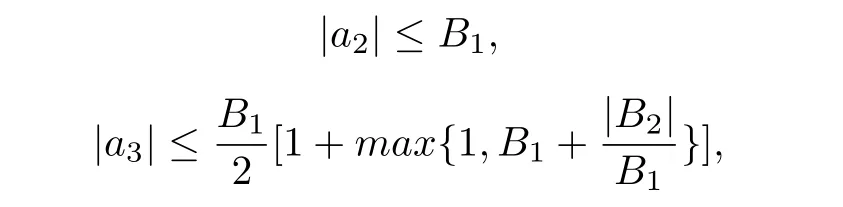
and,for any complex numberµ,

Corollary 2.3[7]Iff(z)∈Abelongs toCq(φ),then

and,for any complex numberµ,

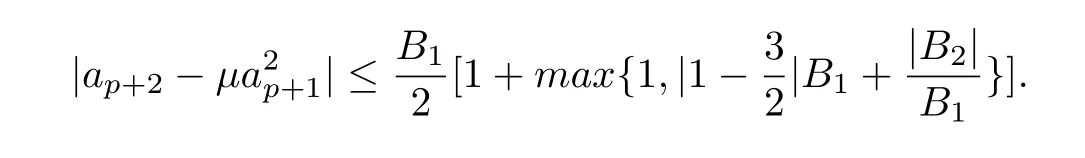
Theorem 2.4Iff(z)∈Apsatis fies

then the following inequalities hold

and,for any complex numberµ,

where

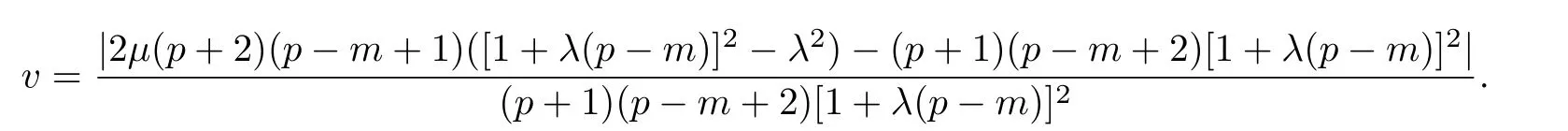
ProofThe result follows by takingω(z)=zin the proof of Theorem 2.1.

Theorem 2.5Iff(z)∈Apbelongs toRpm,q(λ,b;φ),then for any real numberµandb＞0

Further,ifσ1≤µ≤σ3,then

Ifσ3≤µ≤σ2,then

For any real numberµandb＜0,

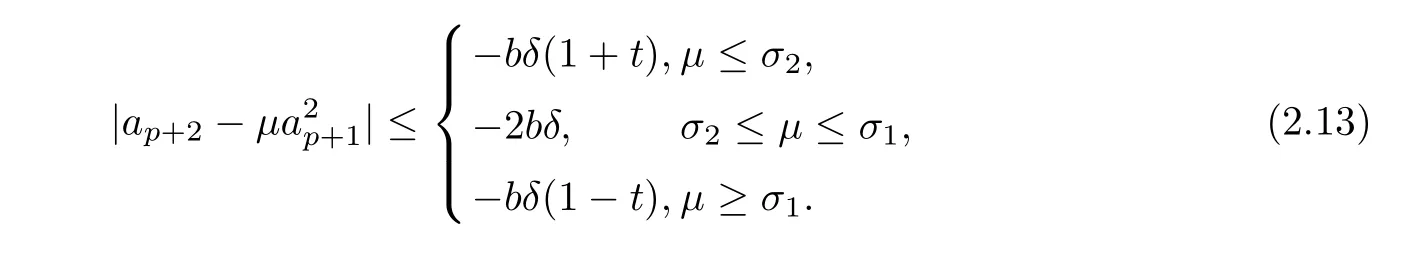
Further,ifσ2≤µ≤σ3,then

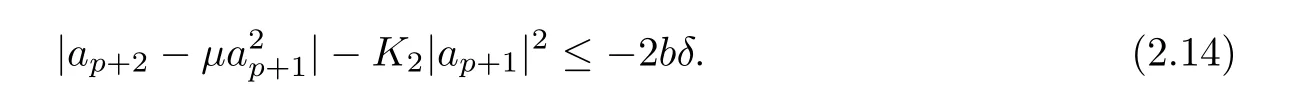
Ifσ3≤µ≤σ1,then

where

ProofWe assume thatb＞0.From(2.2),we have

Ifµ≤σ1,thent≤−1.Thus,by applying Lemma 1.3,we get the first inequality in(2.10).

Ifµ≥σ2,thent≥1.Applying Lemma 1.3,we have the last inequality in(2.10).

Whenσ1≤µ≤σ2,then|t|≤1.Thus applying Lemma 1.3,we obtain the middle inequality in(2.10).

Moreover,(2.11)and(2.12)are established by an application of Lemma 1.3.

Applying Lemma 1.3,we can prove(2.13)−(2.15)forb＜0.The proof of theorem 2.5 is complete.

Corollary 2.6Iff(z)∈Abelongs to(φ),then for any real numberµ

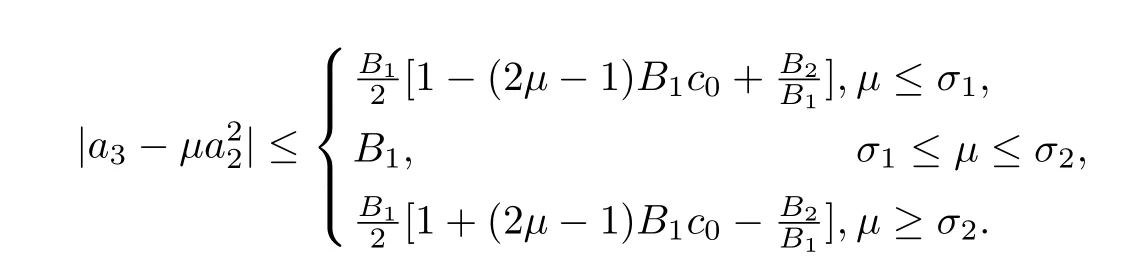
Further,ifσ1≤µ≤σ3,then

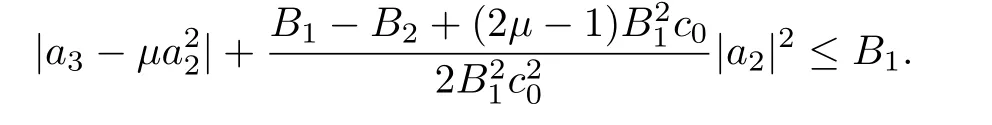
Ifσ3≤µ≤σ2,then

[1]LITTLEWOOD J E.Lectures on the Theory of Functions.Oxford University Press,1944.

[2]MA W,MINDA D.A unified treatment of some special classes of univalent functions[C].Conference Proceedings Lecture Notes Analysis,Cambridge:International Press,1994,157-169.

[3]ROBERTSON M S.Quasi-subordination and coefficient conjectures[J].Bulletin of the American Mathematical Society,1970,76:1-9.

[4]ALTMATS O,OWA S.Majorizations and quasi-subordinations for certain analytic functions[J].Proceedings of the Japan Academy,1982,68(7):181-185.

[5]Lee S Y.Quasi-subordinate functions and coefficient conjectures[J].Journal of the Korean Mathematical Society,1975,12(1):43-50.

[6]REN F Y,OWA S,FUKUI S.Some inequalities on quasi-subordinate functions[]J.Bulletin of the Australian Mathematical Society,1991,43(2):317-324.

[7]MOHD M M,DARUS M.Fekete-Szegö problems for quasi-subordination classes[J].Abstract and Applied Analysis,2012,3(2):1-14.

[8]FRASIN B A.Neighborhoods of certain multivalent functions with negative coefficients[J].Appl Math Comput,2007,193:1-6.

[9]AHUJA O P,JAHANGIRI M.Fekete-Szegö problem for a uni fied class of analytic functions[J].Panamerican Mathematical Journal,1997,7(2):67-78.

[10]ALI R M,Lee S K,RAVICHANDRAN V,et al.The Fekete-Szegö coefficient functional for transforms of analytic functions[J].Bulletin of the Iranian Mathematical Society,2009,35(2):119-142.

[11]CHO N E,OWA S.On the Fekete-Szegö problem for stronglyα-logarithmic quasiconvex functions[J].Southeast Asian Bulletin of Mathematics,2004,28(3):420-430.

[12]CHOI J H,KIM Y C,SUGAWA T.A general approach to the Fekete-Szegö problem[J].Journal of the Mathematical Society of Japan,2007,59(3):707-727.

[13]DARUS M,TUNESKI N.On the Fekete-Szegö problem for generalized close-to-convex functions[J].International Mathematical Journal,2003,4(6):561-568.

[14]DARUS M,SHANMUGAM T N,SIVASUBRAMANIAN S.Fekete-Szegö inequality for a certain class of analytic functions[J].Math Tome,2007,49(72):29-34.

[15]DIXIT K K,PAL S K.On a class of univalent functions related to complex order[J].Indian Journal of Pure and Applied Mathematics,1995,26(9):889-896.

[16]KANAS S.An uni fied approach to the Fekete-Szegö problem[J].Applied Mathematics and Computation,2012,218:8453-8461.

[17]KANAS S,DARWISH H E.Fekete-Szegö problem for starlike and convex functions of complex order[J].Applied Mathematics Letters,2010,23(7):777-782.

[18]KANAS S,LECKO A.On the Fekete-Szegö problem and the domain of convexity for a certain class of univalent functions[J].Zeszyty Naukowe Politechniki Rzezowskiej.Matematyka i Fizyka,1990,10:49-57.

[19]KWON O S,CHO N E.On the Fekete-Szegö problem for certain analytic functions[J].Journal of the Korea Society of Mathematical Education,2003,10(4):265-271.

[20]RAVICHANDRAN V,DARUS M,KHAN M H,et al.Fekete-Szegö inequality for certain class of analytic functions[J].The Australian Journal of Mathematical Analysis and Applications.2004,1(2):2-7.

[21]RAVICHANDRAN V,GANGADHARAN A,DAURS M.Fekete-Szegö inequality for certain clas of Bazilevic functions[J].Far East Journal of Mathematical Sciences,2004,15(2):171-180.

[22]SRUTHA B,PREMA S.Coefficient problem for certain subclass of analytic functions using quasi-subordination[J].Mathematics and Decision sciences,2013,13(6):47-53.

[23]SRUTHA B,LOKESH P.Fekete-Szegö problem for certain subclass of analytic univalent function using quasi-subordination.Mathematica Aeterna,2013,3(3):193-199.

[24]KEOGH F R,MERKES E P.A coefficient inequality for certain classes of analytic functions[J].Proc Amer Math Soc,1969,20:8-12.

[25]NEHARI Z.Conformal mapping.Dover,New York,NY,USA,Reprinting of the 1952 edition(1975).