A Kind of Identities Involving Complete Bell Polynomials
2017-03-14
(1.Department of Mathematics,Luoyang Normal College,Luoyang 471934,China;2.Department of Mathematics and Physical,Luoyang Institute of Science and Technology,Luoyang 471023,China)
§1.Introduction
Many interestingq-series identities can be obtained by derivative,see[3-6].Ismail[3]obtained the two following identities by the method of higher order derivatives.

and


In this paper we will establish a formula of higher derivative byFa`a di Brunoformula,and apply it to some exiting results to get some identities involving complete Bell polynomials.Especially we shall give another expression of(1.1)and(1.2)by complete Bell polynomials.
First we give some definitions and lemmas which will be useful throughout this paper.
Theq−shifted factorial is defined by

Whenn→∞,we de fine

The falling factorialzof orderkis defined by

Theq-gamma function Γq(x)is defined by

and
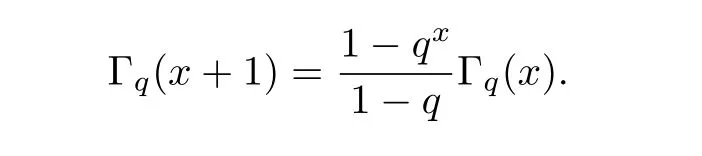
The generalizedq-binomial coefficients are defined by

The generalizedq-harmonic numbers can be defined by

The(exponential)partial Bell polynomialsBn,k=Bn,k(x1,x2,···,xn−k+1)are defined by

Lemma 1[1,p.134TheoremA]The partial Bell polynomials have integral coefficients,are homogeneous of degreek,and of weightn;their exact expression is

where the summation takes place over all integersc1,c2,···,≥0,such that

Lemma 2[1,p.137TheoremA(Fa`adiBrunoformula)]Letfandgbe two formal(Taylor)series:

and lethbe the formal(Taylor)series of the composition ofgbyf.

Hence,coefficientshnare given by the following expression:

where theBn,kare the exponential Bell polynomials.
§2.Main Results and Their Proofs
Theorem 1Letf(x)be analytic function and

Suppose thath(m+1)(x)is themorder derivative ofh(1)(x)form∈N.Then

ProofBy(2.1),we have

So

whereCis an arbitrary constant.By(2.2),we have

On one hand,let

It is easy to see that

On the other hand,byFa`a di Brunoformula,we have

Comparing the coefficients oftn/n!in(2.3)and(2.4),we complete the proof of the theorem.
Corollary 1Leta∈R,n,p∈N and|q|<1.Then

ProofWe have

and

By Theorem 2.1,we complete the proof of the corollary.
Corollary 2Leta∈R,n,p∈N and|q|<1.Then


ProofWe have

and

By Theorem 2.1,we complete the proof of the corollary.
Corollary 3Leta∈R,n,p∈N,|q|<1 andz/=0.Then

where

ProofWe have

and


By Theorem 1,we complete the proof of the corollary.
Corollary 4Leta∈R,n,p∈N,|q|<1 andz/=0.Then

ProofWe have

and

By Theorem 1,we have

By Lemma 1,(2.5)can be written as

The proof of the corollary is completed.
§3.Applications
Theorem 2Letm,n∈N and|q|<1.Then

ProofThe following identity is[3,(2.6)]

it can be rewritten as follows.

Differentiating(3.3)with respect to the variablezformtimes,and by Corollary 0.2 we complete the proof of the theorem.
By(1.1)and(3.1)we get
Corollary 5Letm,n∈N and|q|<1.Then

Theorem 3Letm,n∈N and|q|<1.Then

ProofThe following identity is[3,(2.7)]

it can be rewritten as follows.

Differentiating(3.6)with respect to the variablezform−1 times,and by Corollary 0.2 we complete the proof of the theorem.
Comparing the coefficients ofxj−(−1)jon the right side of(1.2)and(3.4),we obtain
Corollary 6Letm,n∈N and|q|<1.Then

MacMahon[4,vol.2,p.323]get

and(3.7)can be considered as a finite form of the well-known Jacobi triple product identity.
Differentiating this identity with respect to the variablex,then we have
Theorem 4Letm,n,i∈N and|q|<1.Then

whereh(i)=
ProofTakingx→xq−1in(3.7),we have

differentiating(3.7)with respect to the variablexforstimes and by Corollary 1 and Corollary 3,we complete the proof of the theorem.
Takings=1 in Theorem 4,then
Corollary 7Letm,n∈N and|q|<1.Then

Takingx=in Corollary 7,then
Corollary 8Letm<n∈N and|q|<1.Then

Corollary 9Letm∈N and|q|<1.Then

ProofTakingm=nin Corollary 7,we have

Takingin(3.10),we complete the proof of the corollary.
Corollary 10Letm∈N and|q|<1.Then

ProofApplying the operatorto Corollary 7,we have

By the same method as Corollary 9,we have

we complete the proof of the corollary.
General methods of derivation of q-series identities are given in Theorem 0.1 and relevant corollaries.By these methods a kind ofq-series identities withq-Harmonic numbers and complete Bell polynomials are established.As application,we generalized some important q-series identities by higher derivative and got some interesting results in the third part.Whenq→1,a series of combinatorial identities withq-Harmonic numbers and complete Bell polynomials can be found.Some of combinatorial identities play important roles in number theory and analysis.
[1]COMTET L.Advanced Combinatorics[M].Paris:Universitaires de France Presses,1970.
[2]GEORGE G,Mizan R.Basic Hypergeometric Series[M].Cambridge:seconded.,Cambridge University Press,2004.
[3]M,Dennis S.Some combintorial and analytical identities[J],Ann.Comb.2012,16(4),755-771.
[4]MACMAHON P.Combinatory Analysis vol.I,II[M].New York:Reprinted by Chelsea,1960.
[5]ANTHONY S.Reciprocal power sums[J].INTEGERS,2012,12,A39.
[6]Yang Ji-zhen,Wang Yun-peng.A Kind of Identities for Products Reciprocals of q-binomial Coefficients[J].Chin.Quart.J.of Math.2014,29(4):573-582.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Fekete-Szegö Problem for Certain Subclass of p-Valent Analytic Functions using Quasi-Subordination
- Global Stability of A Stochastic Predator-prey Model with Stage-structure
- Convergence Rate of Estimator for Nonparametric Regression Model under-mixing Errors
- Recover Implied Volatility in Short-term Interest Rate Model
- Adjacent Vertex Distinguishing I-total Coloring of Outerplanar Graphs
- The 1-Good-neighbor Connectivity and Diagnosability of Locally Twisted Cubes
