The 1-Good-neighbor Connectivity and Diagnosability of Locally Twisted Cubes

(School of Mathematics and Information Science,Henan Normal University,Xinxiang,Henan 453007,PR China)

§1.Introduction

Many multiprocessor systems have interconnection networks(networks for short)as underlying topologies and a network is usually represented by a graph where nodes represent processors and links represent communication links between processors.We use graphs and networks interchangeably.For the system,study the topological properties of its network is important.Furthermore,some processors may fail in the system,so processor fault identification plays an important role for reliable computing.The first step to deal with faults is to identify the faulty processors from the fault-free ones.The identification process is called the diagnosis of the system.A systemGis said to bet-diagnosable if all faulty processors can be identified without replacement,provided that the number of presented faults does not exceedt.The diagnosability ofGis the maximum value oftsuch thatGist-diagnosable[1]-[3],[4].For at-diagnosable system,Dahbura and Masson[1]proposed an algorithm with time complexO(n2.5),which can effectively identify the set of faulty processors.

Several diagnosis models were proposed to identify the faulty processors.One major approach is the Preparata,Metze,and Chiens(PMC)diagnosis model introduced by Preparata et al.[5].The diagnosis of the system is achieved through two linked processors testing each other.Another important model,namely the comparison diagnosis model(MM model),was proposed by Maeng and Malek[6].In the MM model,to diagnose a system,a node sends the same task to two of its neighbors,and then compares their responses.In 2005,Lai et al.[4]introduced a restricted diagnosability of a multiprocessor system called conditional diagnosability.They consider the situation that no faulty set can contain all the neighbors of any vertex in the system.In 2012,Peng et al.[7]proposed a new measure for faulty diagnosis of the system,namely,theg-good-neighbor diagnosability(which is also called theg-good-neighbor conditional diagnosability),which requires that every fault-free node has at leastgfault-free neighbors.In[7],they studied theg-good-neighbor diagnosability of then-dimensional hypercube under PMC model.In[8],Wang and Han studied theg-good-neighbor diagnosability of then-dimensional hypercube under the MM∗model.Yuan et al.[9],[10]studied that theg-good-neighbor diagnosability of thek-aryn-cube(k≥3)under the PMC model and MM∗model.The Cayley graphCΓngenerated by the transposition tree Γnhas recently received considerable attention.In[11],[12],Wang et al.studied theg-good-neighbor diagnosability ofCΓnunder the PMC model and MM∗model forg=1,2.In this paper,the 1-good-neighbor diagnosability of the locally twisted cubeLTQnhas been studied under the PMC model and MM∗model.It is proved that the 1-good-neighbor connectivityκ(1)(LTQn)=2n−2 and the 1-good-neighbor diagnosability ofLTQnis 2n−1 under the PMC model forn≥4 and the MM∗model forn≥5.

§2.Preliminaries

2.1 Notations

The graph is applied widely[13],[14].In this paper,a multiprocessor system is modeled as an undirected simple graphG=(V,E),whose vertices(nodes)represent processors and edges(links)represent communication links.Given a nonempty vertex subsetV′ofV,the subgraph induced byV′inG,denoted byG[V′],is a graph,whose vertex set isV′and the edge set is the set of all the edges ofGwith both endpoints inV′.The degreedG(v)of a vertexvis the number of edges incident withv.The minimum degree is denoted byδ(G).For any vertexv,we de fine the neighborhoodNG(v)ofvinGto be the set of vertices adjacent tov.uis called a neighbor vertex or a neighbor ofvforu∈NG(v).LetS⊆V(G).NG(S)denotes the set∪v∈SNG(v)S.For neighborhoods and degrees,we will usually omit the subscript for the graph when no confusion arises.A graphGis said to bek-regular if for any vertexv,dG(v)=k.LetGbe a connected graph.The connectivityκ(G)ofGis the minimum number of vertices whose removal results in a disconnected graph or only one vertex left whenGis complete.LetG=(V,E).A fault setF⊆Vis called ag-good-neighbor conditional faulty set if|N(v)∩(VF)|≥gfor every vertexvinVF.Ag-good-neighbor cut ofGis ag-good-neighbor faulty setFsuch thatG−Fis disconnected.The minimum cardinality ofg-good-neighbor cuts is said to be theg-good-neighbor connectivity ofG,denoted byκ(g)(G).A connected graphGis said to beg-good-neighbor connected ifGhas ag-good-neighbor cut.LetF1andF2be two distinct subsets ofV,and let the symmetric differenceF1△F2=(F1F2)∪(F2F1).For graph-theoretical terminology and notation not defined here we follow[15].

2.2 The PMC Model and the MM∗model

For a multiprocessor systemG=(V(G),E(G)),one important diagnosis model,namely the PMC model,was proposed by Preparata et al.[5].In the PMC model,two adjacent processors can perform tests on each other.For two adjacent verticesuandvinV(G),the ordered pair(u,v)represents the test performed byuonv.The outcome of a test(u,v)is either 1 or 0 with the assumption that the testing result is regarded as reliable if the vertexuis fault-free.However,the outcome of a test(u,v)is unreliable,provided that the testeruitself is originally a faulty processor.Suppose that the vertexuof(u,v)is fault-free,then the result would be 0(resp.1)ifvis fault-free(resp.faulty).A test assignmentTforGis a collection of tests for every adjacent pair of vertices.It can be modeled as a directed testing graphT=(V(G),L),where(u,v)∈Limplies thatuandvare adjacent inG.The collection of all test results for a test assignmentTis called a syndrome.Formally,a syndrome is a functionσ:L→{0,1}.The set of all faulty processors in the system is called a faulty set.This can be any subset ofV(G).For a given syndromeσ,a subset of verticesF⊆V(G)is said to be consistent withσif syndromeσcan be produced from the situation that,for any(u,v)∈Lsuch thatu∈VF,σ(u,v)=1 if and only ifv∈F.This means thatFis a possible set of faulty processors.Since a test outcome produced by a faulty processor is unreliable,a given setFof faulty vertices may produce a lot of different syndromes.On the other hand,different faulty sets may produce the same syndrome.Letσ(F)denote the set of all syndromes whichFis consistent with.

Under the PMC model,two distinct setsF1andF2inV(G)are said to be indistinguishable ifσ(F1)∩σ(F2)/=∅,otherwise,F1andF2are said to be distinguishable.Besides,we say that(F1,F2)is an indistinguishable pair ifσ(F1)∩σ(F2)/=∅;else,(F1,F2)is a distinguishable pair.

Using the MM model,the diagnosis is carried out by sending the same testing task to a pair of processors and comparing their responses.Under the MM model,we always assume the output of a comparison performed by a faulty processor is unreliable.The comparison scheme of a systemG=(V(G),E(G))is modeled as a multigraph,denoted byM=(V(G),L),whereLis the labeled-edge set.A labeled edge(u,v)w∈Lrepresents a comparison in which two verticesuandvare compared by a vertexw,which impliesuw,vw∈E(G).The collection of all comparison results inM=(V(G),L)is called the syndrome,denoted byσ∗,of the diagnosis.If the comparison(u,v)wdisagrees,thenσ∗((u,v)w)=1,otherwise,σ∗((u,v)w)=0.Hence,a syndrome is a function fromLto{0,1}.The MM*model is a special case of the MM model.In the MM*model,all comparisons of G are in the comparison scheme ofG,i.e.,ifuw,vw∈E(G),then(u,v)w∈L.

Similarly to the PMC model,we can de fine a subset of verticesF⊆V(G)is consistent with a given syndromeσ∗and two distinct setsF1andF2inV(G)are indistinguishable(resp.distinguishable)under the MM*model.

A systemG=(V,E)isg-good-neighbort-diagnosable ifF1andF2are distinguishable,for each distinct pair ofg-good-neighbor faulty subsetsF1andF2ofVwith|F1|≤tand|F2|≤t.Theg-good-neighbor diagnosabilitytg(G)ofGis the maximum value oftsuch thatGisg-good-neighbort-diagnosable.

2.3 Locally twisted cubes

For an integern≥1,a binary string of lengthnis denoted byu1u2...un,whereui∈{0,1}for every integeri∈{1,2,...,n}.Then-dimensional locally twisted cube,denoted byLTQn,is ann-regular graph of 2nvertices andn2n−1edges,which can be recursively defined as follows[16].

Definition 2.1[16]Forn≥2,ann-dimensional locally twisted cube,denoted byLTQn,is defined recursively as follows:

1)LTQ2is a graph consisting of four nodes labeled with 00,01,10 and 11,respectively,connected by four edges{00,01},{01,11},{11,10}and{10,00}.

2)Forn≥3,LTQnis built from two disjoint copies ofLTQn−1according to the following steps:Let 0LTQn−1denote the graph obtained from one copy ofLTQn−1by pre fixing the label of each node with 0.Let 1LTQn−1denote the graph obtained from the other copy ofLTQn−1by pre fixing the label of each node with 1.Connect each node 0u2u3···unof 0LTQn−1to the node 1(u2+un)u3···unof 1LTQn−1with an edge,where ”+” represents the modulo 2 addition.

Figs.1 and 2 show three examples of locally twisted cubes.The locally twisted cube can also be equivalently defined in the following non-recursive fashion.

Definition 2.2[16]Forn≥2,then-dimensional locally twisted cube,denoted byLTQn,is a graph with{0,1}nas the node set.Two nodesu1u2···unandv1v2···vnofLTQnare adjacent if and only if either one of the following conditions are satisfied.

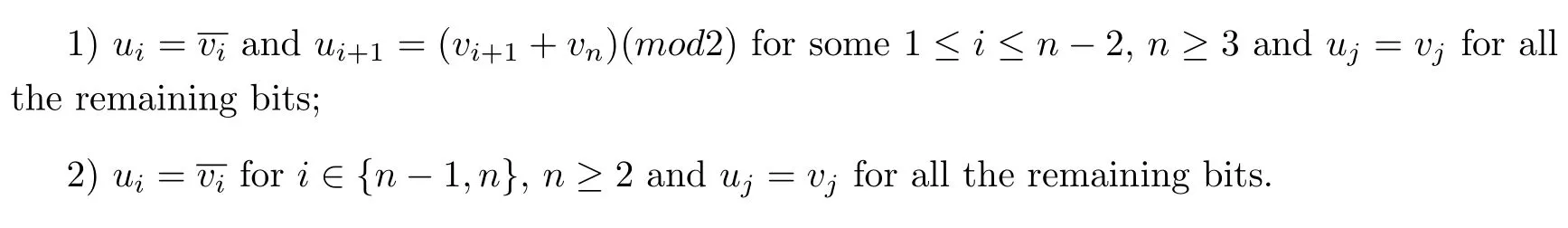
Proposition 2.3LetLTQnbe the locally twisted cube.If two verticesu,vare adjacent,then there is no common neighbor vertex of these two vertices,i.e.,|N(u)∩N(v)|=0.If two verticesu,vare not adjacent,then there are at most two common neighbor vertices of these two vertices,i.e.,|N(u)∩N(v)|≤2.

ProofLetu,v∈V(LTQn).The proof is by induction onn.Forn=2,LTQ2is a 4-cycle.Therefore,if two verticesu,vare adjacent,then|N(u)∩N(v)|=0;if two verticesu,vare not adjacent,then|N(u)∩N(v)|≤2.Assumen≥2 and the result holds forLTQn−1.Suppose thatu,v∈V(iLTQn−1)fori∈{0,1}.Ifuis adjacent tov,by the inductive hypothesis,the result holds iniLTQn−1.Since the edges whose end vertices in differentiLTQn−1’s are a matching,|N(u)∩N(v)|=0 holds.Ifuis not adjacent tov,by the inductive hypothesis,then the result holds iniLTQn−1.Since the edges whose end vertices in differentiLTQn−1’s are a matching,|N(u)∩N(v)|≤2 holds.So we suppose thatu∈V(0LTQn−1)andv∈V(1LTQn−1).Since the edges whose end vertices in differentiLTQn−1’s are a matching,|N(u)∩N(v)|≤2.

Fig.1.LTQ2and LTQ3

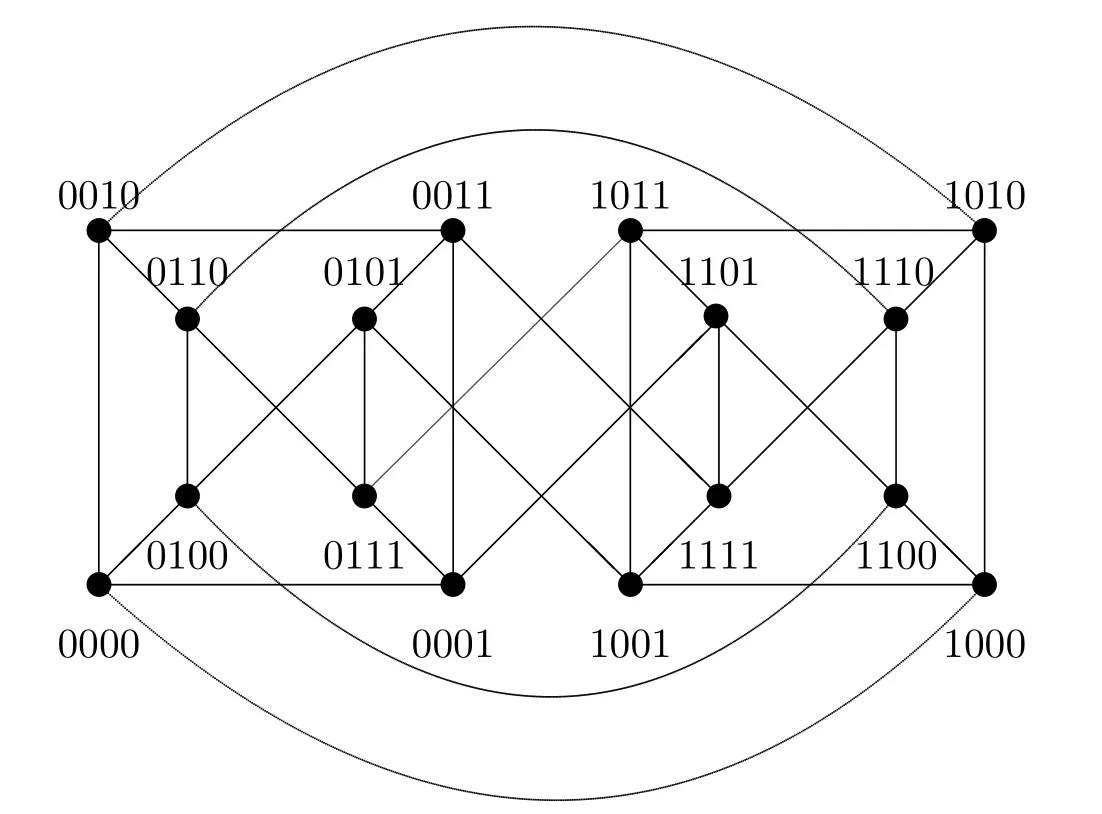
Fig.2.LTQ4

§3.The 1-Good-neighbor Connectivity of Locally Twisted Cubes

In this section,we shall show theg-good-neighbor connectivity of the locally twisted cubeLTQn.

Theorem 3.1[16]LetLTQnbe the locally twisted cube.Thenκ(LTQn)=n.

Lemma 3.2[17]LetLTQnbe the locally twisted cube,and letS⊆V(LTQn)andn≥3.Suppose thatLTQn−Sis disconnected.The following two conditions hold:

(1)|S|≥n;

(2)Ifn≤|S|≤2n−3,thenLTQn−Shas exactly two components,one is trivial and the other is nontrivial.

Lemma 3.3LetAbe defined as above and letLTQnbe the locally twisted cube.IfF1=NLTQn(A),F2=F1∪A,then|F1|=2n−2,|F2|=2n,andδ(LTQn−F1−F2)≥1.

ProofSinceA={0n−1X:X∈{0,1}}and the definition ofLTQn,we haveLTQn[A]2and|A|=2.By Proposition 2.3,|F1|=n−1+n−1=2n−2 and|F2|=2n.

Claim 1LTQn−F2is connected.

The proof of this claim is by induction onn.Forn=4,F1={0100,0111,0010,0011,1101,1000}andF2={0000,0001,0100,0111,0010,0011,1101,1000}.It is easy to see thatLTQ4−F2is connected(See Fig.2).Assume thatn≥5 andLTQn−1−F2is connected.Let=F2∩V(iLTQn−1)fori=0,1.By Definition 2.1,A⊆V(0LTQn−1),0LTQn−1is connected and|N(A)∩V(1LTQn−1)|=2.By Theorem 3.1,1LTQn−1is connected.Note that|F2|=2n.Sincen≥5,22−1＞2nholds.Therefore,LTQn−F2is connected by De finition 2.1.

By Claim 1,δ(LTQn−F1−F2)≥1.

Lemma 3.4LetLTQnbe the locally twisted cube.Then 1-neighbor-connectivityκ(1)(LTQn)≤2(n−1).

ProofLetF1andF2be defined in Lemma 3.3.Note thatLTQn−F1has two componentsLTQn−F2andK2.By Lemma 4.4,F1is ag-good-neighbor cut.By the definition of 1-goodneighbor connectivity,we haveκ1(LTQn)≤2(n−1).

Theorem 3.5LetLTQnbe the locally twisted cube.Thenκ(1)(LTQn)=2n−2 forn≥4.

ProofLetFbe an arbitrary subset ofV(LTQn)such that|F|≤2n−3.Suppose that|F|≤n−1.By Theorem 3.1,LTQn−Fis connected.Suppose thatn≤|F|≤2n−3.By Lemma 3.2,LTQn−Fhas two components:an isolated vertex and a nontrivial subgraph.Therefore,Fis not a 1-good-neighbor cut ofLTQn.Thus,κ1(LTQn)≥2n−2.By Lemma 3.4,we haveκ1(LTQn)=2n−2 forn≥4.

§4.The 1-Good-neighbor Diagnosability of the Locally Twisted Cube LTQnunder the PMC Model

In this section,we shall show the 1-good-neighbor diagnosability of locally twisted cubes under the PMC model.

Theorem 4.1[9]A systemG=(V,E)isg-good-neighbort-diagnosable under thePMCmodel if and only if there is an edgeuv∈Ewithu∈V(F1∪F2)andv∈F1△F2for each distinct pair ofg-good-neighbor faulty subsetsF1andF2ofVwith|F1|≤tand|F2|≤t.

Lemma 4.2A graph of minimum degree 1 has at least two vertices.

The proof of Lemma 4.2 is trivial.

Lemma 4.3Letn≥4.Then the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder the PMC model is less than or equal to 2n−1,i.e.,t1(LTQn)≤2n−1.

Proof LetAbe defined in Lemma 2,and letF1=NLTQn(A),F2=A∪NLTQn(A).By Lemma 3.3,|F1|=2n−2,|F2|=|A|+|F1|=2n,δ(LTQn−F1)≥1 andδ(LTQn−F2)≥1.Therefore,F1andF2are 1-good-neighbor faulty sets ofLTQnwith|F1|=2n−2 and|F2|=2n.SinceA=F1△F2andNLTQn(A)=F1⊂F2,there is no edge ofLTQnbetweenV(LTQn)(F1∪F2)andF1△F2.By Theorem 4.1,we can deduce thatLTQnis not 1-goodneighbor 2n-diagnosable under the PMC model.Hence,by the de finition of 1-good-neighbor diagnosability,we conclude that the 1-good-neighbor diagnosability ofLTQnis less than 2n,i.e.,t1(LTQn)≤2n−1.

Lemma 4.4Letn≥4.Then the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder the PMC model is more than or equal to 2n−1,i.e.,t1(LTQn)≥2n−1.

ProofBy the definition of 1-good-neighbor diagnosability,it is sufficient to show thatLTQnis 1-good-neighbor(2n−1)-diagnosable.By Theorem 4.1,to proveLTQnis 1-goodneighbor(2n−1)-diagnosable,it is equivalent to prove that there is an edgeuv∈E(LTQn)withu∈V(LTQn)(F1∪F2)andv∈F1△F2for each distinct pair of 1-good-neighbor faulty subsetsF1andF2ofV(LTQn)with|F1|≤2n−1 and|F2|≤2n−1.

We prove this statement by contradiction.Suppose that there are two distinct 1-goodneighbor faulty subsetsF1andF2ofLTQnwith|F1|≤2n−1 and|F2|≤2n−1,but the vertex set pair(F1,F2)is not satisfied with the condition in Theorem 4.1,i.e.,there are no edges betweenV(LTQn)(F1∪F2)andF1△F2.Without loss of generality,assume thatF2F1/=∅.Assume thatV(LTQn)=F1∪F2.Sincen≥4,we have that 2n=|V(LTQn)|=|F1∪F2|=|F1|+|F2|−|F1∩F2|≤|F1|+|F2|≤2n−1+2n−1≤4n−2,a contradiction.Therefore,V(LTQn)/=F1∪F2.

Since there are no edges betweenV(LTQn)(F1∪F2)andF1△F2,andF1is a 1-goodneighbor faulty set,LTQn−F1has two partsLTQn−F1−F2andLTQn[F2F1].Thus,δ(LTQn−F1−F2)≥1 andδ(LTQn[F2F1])≥1.Similarly,δ(LTQn[F1F2])≥1 whenF1F2/=∅.Therefore,F1∩F2is also a 1-good-neighbor faulty set.Since there are no edges betweenV(LTQn−F1−F2)andF1△F2,F1∩F2is also a 1-good-neighbor cut.WhenF1F2=∅,F1∩F2=F1is also a 1-good-neighbor faulty set.Since there are no edges betweenV(LTQn−F1−F2)andF1△F2,F1∩F2is a 1-good-neighbor cut.By Theorem 3.5,|F1∩F2|≥2n−2.By Lemma 4.2,|F2F1|≥2.Therefore,|F2|=|F2F1|+|F1∩F2|≥2+2n−2=2n,which contradicts with that|F2|≤2n−1.SoLTQnis 1-good-neighbor(2n−1)-diagnosable.By the de finition oft1(LTQn),t1(LTQn)≥2n−1.

Combining Lemmas 4.3 and Lemma 4.4,we have the following theorem.

Theorem 4.5Letn≥4.Then the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder the PMC model is 2n−1.

§5.The 1-Good-neighbor Diagnosability of Locally Twisted Cubes Under the MM∗Model

Before discussing the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder the MM∗model,we first give an existing result.

Theorem 5.1([1],[9])A systemG=(V,E)isg-good-neighbort-diagnosable under theMM∗model if and only if each distinct pair ofg-good-neighbor faulty subsetsF1andF2ofVwith|F1|≤tand|F2|≤tsatisfies one of the following conditions.

(1)There are two verticesu,w∈V(F1∪F2)and there is a vertexv∈F1△F2such thatuw∈Eandvw∈E.

(2)There are two verticesu,v∈F1F2and there is a vertexw∈V(F1∪F2)such thatuw∈Eandvw∈E.

(3)There are two verticesu,v∈F2F1and there is a vertexw∈V(F1∪F2)such thatuw∈Eandvw∈E.

Lemma 5.1Letn≥4.Then the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder the MM∗model is less than or equal to 2n−1,i.e.,t1(LTQn)≤2n−1.

ProofLetAbe defined in Lemma 3.3,and letF1=NLTQn(A),F2=A∪NLTQn(A).By Lemma 3.3,|F1|=2n−2,|F2|=|A|+|F1|=2n,δ(LTQn−F1)≥1 andδ(LTQn−F2)≥1.Therefore,F1andF2are 1-good-neighbor faulty sets ofLTQnwith|F1|=2n−2 and|F2|=2n.By the definitions ofF1andF2,F1△F2=A.NoteF1F2=∅,F2F1=Aand(V(LTQn)(F1∪F2))∩A=∅.Therefore,bothF1andF2are not satisfied with any one condition in Theorem 5.1,andLTQnis not 1-good-neighbor 2n-diagnosable.Hence,t1(LTQn)≤2n−1.

Lemma 5.2Letn≥5.Then the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder the MM∗model is more than or equal to 2n−1,i.e.,t1(LTQn)≥2n−1.

ProofBy the definition of 1-good-neighbor diagnosability,it is sufficient to show thatLTQnis 1-good-neighbor(2n−1)-diagnosable.

By Theorem 5.1,suppose,on the contrary,that there are two distinct 1-good-neighbor faulty subsetsF1andF2ofLTQnwith|F1|≤2n−1 and|F2|≤2n−1,but the vertex set pair(F1,F2)is not satisfied with any one condition in Theorem 5.1.Without loss of generality,assume thatF2F1/=∅.Similarly to the discussion onV(LTQn)=F1∪F2in Lemma 4.4,we can deduceV(LTQn)/=F1∪F2.

Claim 1LTQn−F1−F2has no isolated vertex.

Suppose,on the contrary,thatLTQn−F1−F2has at least one isolated vertexw.SinceF1is a 1-good neighbor faulty set,there is a vertexu∈F2F1such thatuis adjacent tow.Since the vertex set pair(F1,F2)is not satisfied with any one condition in Theorem 5.1,there is at most one vertexu∈F2F1such thatuis adjacent tow.Thus,there is just one vertexu∈F2F1such thatuis adjacent tow.Similarly,we can deduce that there is just one vertexv∈F1F2such thatvis adjacent towwhenF1F2/=∅.LetW⊆V(LTQn)(F1∪F2)be the set of isolated vertices inLTQn[V(LTQn)(F1∪F2)],and letHbe the subgraph induced by the vertex setV(LTQn)(F1∪F2∪W).Then for anyw∈W,there are(n−2)neighbors inF1∩F2whenF1F2/=∅.Since|F2|≤2n−1,we have that∑w∈W|NLTQn[(F1∩F2)∪W](w)|=|W|(n−2)≤∈F1∩F2dLTQn(v)=n|F1∩F2|≤n(|F2|−1)≤n(2n−2)=2n2−2n.It follows that|W|≤≤2n+4 forn≥5.Note|F1∪F2|=|F1|+|F2|−|F1∩F2|≤2(2n−1)−(n−2)=3n.Suppose thatV(H)=∅.Then 2n=|V(LTQn)|=|F1∪F2|+|W|≤3n+2n+4=5n+4.This is a contradiction ton≥5.SoV(H)/=∅.Since the vertex set pair(F1,F2)is not satisfied with the condition(1)of Theorem 5.1,and any vertex ofV(H)is not isolated inH,we deduce that there is no edge betweenV(H)andF1△F2.Thus,F1∩F2is a vertex cut ofLTQnandδ(LTQn−(F1∩F2))≥1,i.e.,F1∩F2is a 1-good-neighbor cut ofLTQn.By Theorem 3.5,|F1∩F2|≥2n−2.Because|F1|≤2n−1,|F2|≤2n−1,and neitherF1F2norF2F1is empty,we have|F1F2|=|F2F1|=1.LetF1F2={v1}andF2F1={v2}.Then for any vertexw∈W,ware adjacent tov1andv2.According to Proposition 2.3,there are at most two common neighbors for any pair of vertices inLTQn,it follows that there are at most two isolated vertices inLTQn−F1−F2.

Suppose that there is exactly one isolated vertexvinLTQn−F1−F2.Letv1andv2be adjacent tov.ThenNLTQn(v){v1,v2}⊆F1∩F2.SinceLTQncontains no triangle,it follows thatNLTQn(v1){v}⊆F1∩F2;NLTQn(v2){v}⊆F1∩F2;[NLTQn(v){v1,v2}]∩[NLTQn(v1){v}]=∅and[NLTQn(v){v1,v2}]∩[NLTQn(v2){v}]=∅.By Proposition 2.3,|[NLTQn(v1){v}]∩[NLTQn(v2){v}]|≤1.Thus,|F1∩F2|≥|NLTQn(v){v1,v2}|+|NLTQn(v1){v}|+|NLTQn(v2){v}|=(n−2)+(n−1)+(n−1)−1=3n−5.It follows that|F2|=|F2F1|+|F1∩F2|≥1+3n−5=3n−4＞2n−1(n≥4),which contradicts|F2|≤2n−1.

Suppose that there are exactly two isolated verticesvandwinLTQn−F1−F2.Letv1andv2be adjacent tovandw,respectively.ThenNLTQn(v){v1,v2}⊆F1∩F2.SinceLTQncontains no triangle,it follows thatNLTQn(v1){v,w}⊆F1∩F2,NLTQn(v2){v,w}⊆F1∩F2,[NLTQn(v){v1,v2}]∩[NLTQn(v1){v,w}]=∅and[NLTQn(v){v1,v2}]∩[NLTQn(v2){v,w}]=∅.By Proposition 2.3,there are at most two common neighbors for any pair of vertices inLTQn.Thus,it follows that|[NLTQn(v1){v,w}]∩[NLTQn(v2){v,w}]|=0.Thus,|F1∩F2|≥|NLTQn(v){v1,v2}|+|NLTQn(w){v1,v2}|+|NLTQn(v1){v,w}|+|NLTQn(v2){v,w}|=(n−2)+(n−2)+(n−2)+(n−2)=4n−8.It follows that|F2|=|F2F1|+|F1∩F2|≥1+4n−8=4n−7＞2n−1 (n≥4),which contradicts|F2|≤2n−1.

Suppose thatF1F2=∅.ThenF1⊆F2.SinceF2is a 1-good neighbor faulty set,LTQn−F2=LTQn−F1−F2has no isolated vertex.The proof of Claim 1 is complete.

Letu∈V(LTQn)(F1∪F2).By Claim 1,uhas at least one neighbor inLTQn−F1−F2.Since the vertex set pair(F1,F2)is not satisfied with any one condition in Theorem 5.1,by the condition(1)of Theorem 5.1,for any pair of adjacent verticesu,w∈V(LTQn)(F1∪F2),there is no vertexv∈F1△F2such thatuw∈E(LTQn)andvw∈E(LTQn).It follows thatuhas no neighbor inF1△F2.By the arbitrariness ofu,there is no edge betweenV(LTQn)(F1∪F2)andF1△F2.SinceF2F1/=∅andF1is a 1-good-neighbor faulty set,δ(LTQn−F1−F2)≥1 andδ(LTQn[F2F1])≥1.SinceF2is a 1-good-neighbor faulty set,δ(LTQn[F1F2])≥1 whenF1F2/=∅.Therefore,F1∩F2is a 1-good-neighbor cut ofLTQn.Suppose thatF1F2=∅.ThenF1∩F2=F1.Therefore,F1∩F2is a 1-good-neighbor cut ofLTQnwhenF1F2=∅.By Theorem 3.5,we have|F1∩F2|≥2n−2.By Lemma 4.2,|F2F1|≥2.Therefore,|F2|=|F2F1|+|F1∩F2|≥2+(2n−2)=2n,which contradicts|F2|≤2n−1.Therefore,LTQnis 1-good-neighbor(2n−1)-diagnosable andt1(LTQn)≥2n−1.

Combining Lemmas 5.2 and 5.3,we have the following theorem.

Theorem 5.4Letn≥5.Then the 1-good-neighbor diagnosability of the locally twisted cubeLTQnunder theMM∗model is 2n−1.

[1]DAHBURA A T,MASSON G M.AnO(n2.5)Fault identification algorithm for diagnosable systems[J].IEEE Transactions on Computers,1984,33(6):486-492.

[2]FAN Jian-xi.Diagnosability of crossed cubes under the comparison diagnosis model[J].IEEE Transactions on Parallel and Distributed Systems,2002,13(10):1099-1104.

[3]FAN Jian-xi,ZHANG Shu-kui,JIA Xiao-hua,et al.The Restricted Connectivity of Locally Twisted Cubes[C].10th International Symposium on Pervasive Systems,Algorithms,and Networks(ISPAN).Kaohsiung,14-16 December 2009,574–578.

[4]LAI Pao-Lien,TAN J J M,CHANG Chien-Ping,et al.Conditional Diagnosability Measures for Large Multiprocessor Systems[J].IEEE Transactions on Computers,2005,54(2):165-175.

[5]PREPARATA F.P,METZE G,CHIEN R T.On the connection assignment problem of diagnosable systems[J].IEEE Transactions on Computers,1967,EC-16:848-854.

[6]MAENG J,MALEK M.A comparison connection assignment for self-diagnosis of multiprocessor systems[C].in:Proceeding of 11th International Symposium on Fault-Tolerant Computing,Washington,D C:IEEE Computer Society Press,1981,173-175.

[7]PENG Shao-Lun,LIN Cheng-Kuan,TAN J J M,et al.Theg-good-neighbor conditional diagnosability of hypercube under PMC model[J].Applied Mathematics and Computation,2012,218(21):10406-10412.

[8]WANG Shi-ying,HAN Wei-ping.Theg-good-neighbor conditional diagnosability ofn-dimensional hypercubes under the MM*model[J].Information Processing Letters,2016,116:574-577.

[9]YUAN Jun,LIU Ai-xia,MA Xue,et al.Theg-good-neighbor conditional diagnosability ofk-aryn-cubes under the PMC model and MM∗model[J].IEEE Transactions on Parallel and Distributed Systems,2015,26:1165-1177.

[10]YUAN Jun,LIU Ai-xia,QIN Xiao,et al.g-Good-neighbor conditional diagnosability measures for 3-aryn-cube networks[J].Theoretical Computer Science,2016,622:144-162.

[11]WANG Mu-jiang-shan,GUO Yubao,WANG Shiying.The 1-good-neighbor diagnosability of Cayley graphs generated by transposition trees under the PMC model and MM∗model[J].International Journal of Computer Mathematics,2017,94(3):620-631.

[12]WANG Mu-jiang-shan,LIN Yu-qing,WANG Shi-ying.The 2-good-neighbor diagnosability of Cayley graphs generated by transposition trees under the PMC model and MM*model[J].Theoretical Computer Science 628(2016)92-100.

[13]LIN Hao,LIN Lan.Minimum Dominating Tree Problem for Graphs[J].Chinese Quarterly Journal of Mathematics,2014,29(1):1–8.

[14]WANG Mu-Jiang-shan,YUAN Jun,LIN Shang-wei,et al.Ordered and Hamilton Digraphs,Chinese Quarterly Journal of Mathematics[J].2010,25(3):317-326.

[15]BONDY J A,MURTY U S R..Graph Theory[M].New York:Springer,2007.

[16]YANG Xiao-fan,EVANS D J,MEGSON G M.The Locally Twisted Cubes[J].International Journal of Computer Mathematics,2005(82)(4):401-413.

[17]FENG Rui-tao,BIAN Genq-ing,WANG Xin-ke.Conditional diagnosability of the locally twisted cubes under the PMC model[J].Communications and Network,2011,3:220-224.