Global Existence,Asympotic Behavior and Uniform Attractors for Thermoelastic Systems

(College of Science,Donghua University,Shanghai 201620,China)

§1.Introduction

In this paper,we consider the following thermoelastic system

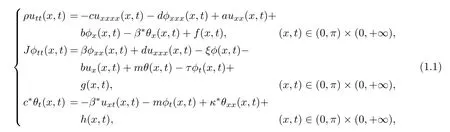
wherea＞0 andc＞0 are elastic coefficients,dandbare positive constant,β∗is a thermal expansion coefficient,βandξare diffusion coefficients,mis a thermal expansion coefficient,τis a viscous coefficient,c∗is the heat capacity,κ∗represents a thermal diffusion coefficient.The mechanical interpretation of the positivity ofρandJis clear.The positivity ofτandκ∗implies that the processes are dissipative.

This system(1.1)is supplemented with boundary conditions

and initial conditions

To guarantee the decay of the solutions(u,φ,θ)to(0,0,0)of the problem(1.1)～(1.3),we should impose that

Now we would like to recall the related results.For the nonlinear form of the strain gradient theory,such as the boundary conditions,the constitutive equations and the equations of motion were reported by Toupin[16-17].Brulin and Hyalmarss[1]and Ryamrz[15]pointed out that the second order displacement gradient should be added to the independent constitutive variables for the investigation of specific nonlocal phenomena.The existence,uniqueness and the exponential decay of the one-dimensional strain gradient theory obtained by Casas and Quintanilla[2].

Qin and Wei[14]established the globule existence of liner and semiliner thermoelastic systems,asymptotic behavior and uniform attractors of non-autonomous thermoelastic systems.Watson[18]proved the unique global solvability of classical solutions to a one-dimensional nonlinear thermoviscoelastic system.Qin[8-9]established the global existence,asymptotic behavior of smooth solutions under more general constitutive assumptions.Qin[10]has improved these results and established the global existence,exponential stability and the global attractors inHi(i=1,2,4).Zheng and Qin[2]and Qin[11]proved the existence of global attractors of the Navier-Stokes equations.

The exponential stability and analyticity of the semigroups associated with dissipative systems have been studied by many authors.For general survey on these topics,we refer to the book by Liu and Zheng[5]and other related models in[4],[19]and[11].

Our aim in this work is to prove the global well-posedness of the thermoelastic system(1.1)～(1.3)and establish its uniform attractors.The outline of this paper is organized as follows.In Section 2,we shall use the semigroup method to prove an existence and uniqueness result of system(1.1)～(1.3).Then,in Section 3,we establish the asymptotic behavior of global solutions using the multiplicative method deal with the semilinear case.In Section 4,we also prove the existence of the uniform attractors.Moreover,the semilinear case is considered in Section 5.

§2.Global Well-posedness

In order to state our main result,we may first rewrite problem(1.1)～(1.3)in an first-order abstract form and produce a vector functionU=(u1,u2,u3,u4,u5)T,then we can use the semigroup method to deduce the well-posedness of this system.

The problem(1.1)～(1.3)is equivalent to the following problem

with boundary conditions

and initial conditions

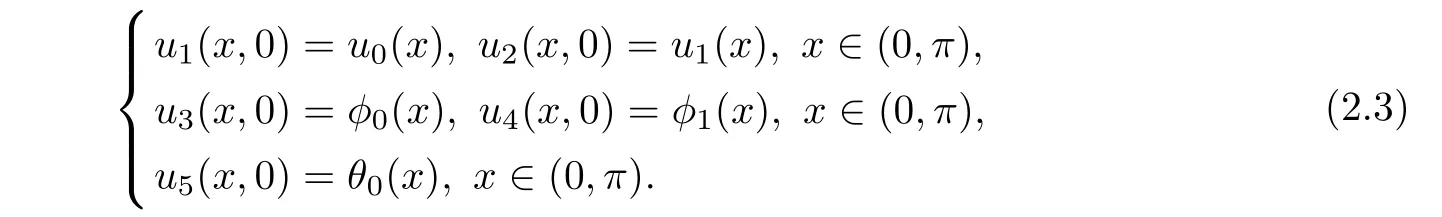
Then system(2.1)～(2.3)is converted to the following abstract ODE

ThusAis a dissipative operator and we can know thatAis a maximal accretive operator and we have(u0,u1,φ0,φ1,θ0)∈D(A)(see,e.g.,Zheng[20].We thus complete the proof.

§3.Uniform Stability

We assume that the constitutive coefficients satisfy

The above assumptions are imposed to guarantee that the internal energy of the system is positive definite,which is related with the well-posedness of the problem in the sense of Hadamard.

In this section,we shall state and prove our decay results,then establish several lemmas.

Lemma 1Let(u,φ,θ)be the solution of problem(1.1)～(1.3).Then the energy functional defined by

satisfies,for anyε＞0,

with some constantsC1＞0,C＞0 andCbeing independent of initial data.

ProofMultiplying(1.1)1～(1.1)3byut,φtandθrespectively,then integrating them over(0,π)and then summing them up and using the boundary conditions,we obtain

Then by Young’s inequalities and Poincaré’s inequality,we obtain(3.2).

Lemma 2Let(u,φ,θ)be the solution of problem(1.1)～(1.3).Then the functionalF1defined by

satisfies,for anyδ＞0,

with some positive constantsC2＞0,C＞0 andCbeing independent of initial data.

ProofBy a direct computing and using(1.1)～1.3),we have

Then by Young’s inequality and Poincaré’s inequality,for anyδ＞0,we can establish(3.5).

Lemma 3Let(u,φ,θ)be the solution of problem(1.1)～(1.3).Then the functionalF2defined by

satisfies,for anyγ＞0,

with some positive constantsC3＞0,C＞0 andCbeing independent of initial data.

ProofBy a direct computing and using(1.1)～(1.3),we have

Then by Young’s inequality and Poincaré’s inequality,we obtain for anyγ′＞0,γ′′＞0,

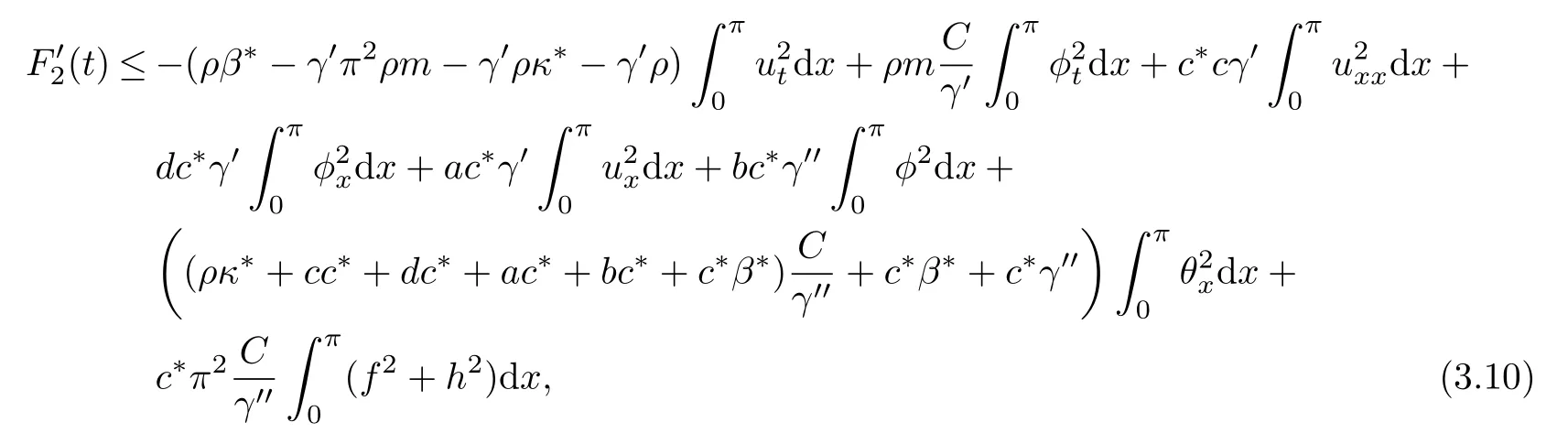
which gives(3.8).

Lemma 4Let(u,φ,θ)be the solution of problem(1.1)～(1.3).Then the functionalF3defined by

satisfies

for some constantsC4＞0,C＞0 andCbeing independent of initial data.

ProofBy(1.1)～(1.3)and a direct computing,we obtain

By Young’s inequality and Poincaré’s inequality,we can establish(3.12).

Lemma 5Suppose thaty(t)∈C1(R+),y(t)≥0,∀t＞0 and satisfies

where 0≤λ(t)≤L1(R+)andC0is a positive constant.Then we have

Furthermore,(1)Ifλ(t)≤∀t＞0,withC1＞0,α0＞0 being constants,then

withC2＞0,α＞0 being constants.

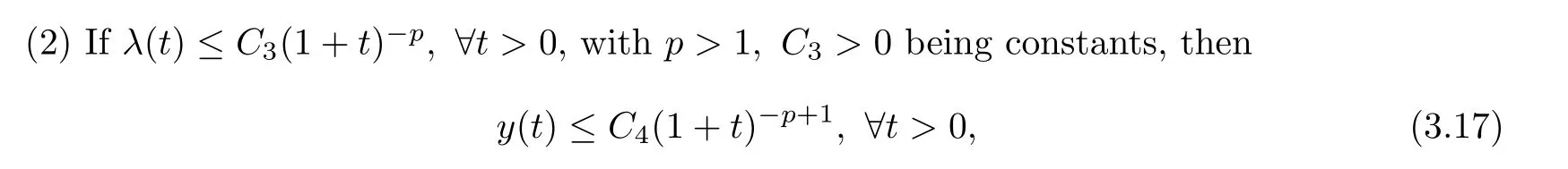
with a constantC4＞0.

withC0＞0 andα0＞0 being constants,then there exist positive constantsM,αsuch that the energyE(t)satisfies

If

with constantsC′＞0,p＞1,then there exists a constantC∗＞0,such that

ProofForN1,N2＞0,we define a Lyapunov functionalLas follows

By using(3.2),(3.5),(3.8)and(3.12),we get

for some constantC′＞0 andC′being independent of initial data.

for some constantγ′＞0.

On the other hand,we see thatL(t)is equivalent toE(t),i.e.,for some constantC＞0 independent oft,we have

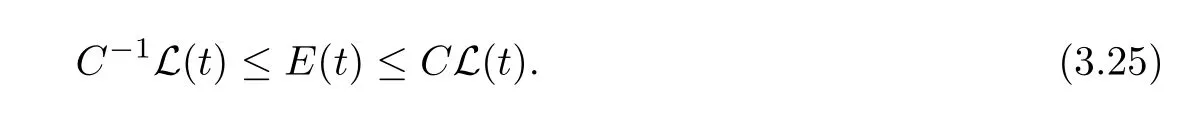
Hence we derive from(3.25)that there exists a constantγ0＞0,such that

Applying Lemma 5 to(3.26),we can conclude(3.18),(3.20)and(3.22).

§4.Uniform Attractors

In this section,we shall establish the existence of uniform attractors for thermoelastic system(1.1).

with boundary conditions

and the initial conditions

Let

The energy of problem(4.1)is given by

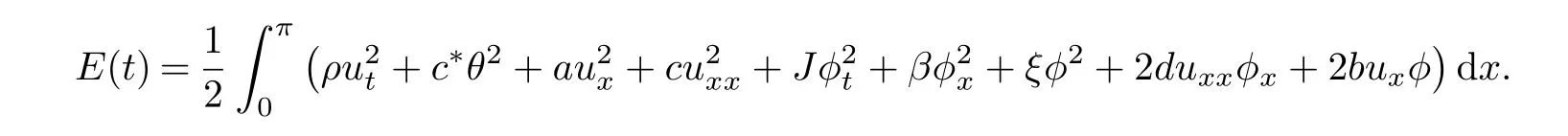
Without loss of generality,we assume thatρ=c∗=a=c=J=β=ξ=d=b=1,then we have

For any(uτ,u1τ,φτ,φ1τ,θτ)∈H1and anyF∈E,we define for allt≥τ,τ≥0,

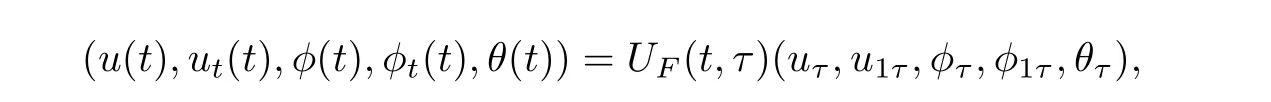
where(uτ,u1τ,φτ,φ1τ,θτ)solves the problem(4.1).Our result concerns the uniform attractor inH1,we define the hull ofF0∈Eas

where[·]Edenotes the closure in Banach spaceE.We note that

Lemma 6Let Σ defined as before andF0∈E,then

ProofSee,e.g.,Chepyzhov and Vishik

Theorem 3Let Σ=[F0(t+h)|h∈R+]E,whereF0∈Eis an arbitrary but fixed symbol function.Then for anyF∈Σ and for any(uτ,u1τ,φτ,φ1τ,θτ)∈H1,τ≥0,problem(4.1)admits a unique global solution(u(t),ut(t),φ(t),φt(t),θ(t))∈H1,which generates a unique semi-process{UF(t,τ)}(t≥τ,τ≥0)onH1of a two-parameter family of operators,such that for anyt≥τ,τ≥0,

First,we shall establish the family of semi-processes{UF(t,τ)}has a bounded uniformly absorbing set given in the following theorem.

Theorem 4Under the assumption(4.4),the family of semi-processes{UF(t,τ)}(F∈Σ,t≥τ,τ≥0),corresponding to(4.1)～(4.3)has a bounded uniformly absorbing setB0inH1.

ProofSimilarly to the proof of Theorem 3.1,we get

whereγ0,C1are two positive constants withC1being independent of initial data.

In the following,C denotes a general positive constant and independent of initial data,which may be different in different estimates.

Obviously,we have

Applying Lemma 4.1 to(4.8),we conclude

Now for any bounded setB0⊆H1,for any(uτ,u1τ,φτ,φ1τ,θτ)∈B0,τ≥0,there exists a constantCB0＞0,such thatE(τ)≤CB0.Taking

then for any t≥t0≥τ,we have

which gives‖(u(t),ut(t),φ(t),φt(t),θ(t))‖H1≤2E(t)Then,we can obtain

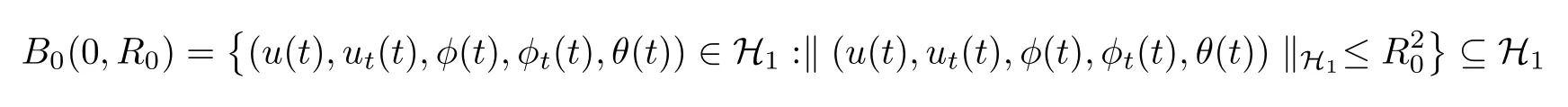
is a uniformly absorbing set for anyF∈Σ,i.e.,for any bounded subsetBinH1,there exists a timet0=t0(τ,F0)≥τ,such that for allt≥t0,

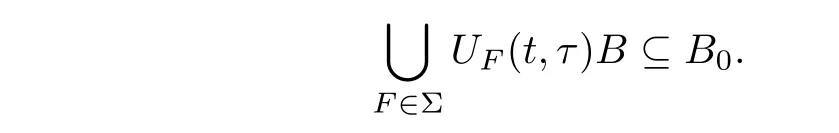
Without loss of generality,we deal with the strong solutions in the sequence,the case for weak solutions then easily follows by a density argument.

ThenW(t)satisfies

where 0≤σ≤π.

Integrating(4.13)over[0,T]with respect toσ,we obtain that

From(4.10)～(4.12),it follows

whereCM=C(T,τ,γ)＞0 is a positive constant.

By Young’s inequality and Poincaré’s inequality,we also know

Thus we conclude

In the sequel,we shall prove the uniformly(w.r.t.F∈Σ)asymptotic compactness inH1,which is stated in the following theorem.

Theorem 5Assume thatFsatisfies(4.4),then the family of semi-process{UF(t,τ)}(F∈Σ,t≥τ,τ≥0),corresponding to(4.1),is uniformly(w.r.t.F∈Σ)asymptotically compact inH1.

ProofSince the family of semi-processes{UF(t,τ)}(F∈Σ,t≥ τ,τ≥0)has a bounded uniformly absorbing set,by the definition ofCM,we know that for any fixedε＞0,we can chooseT＞0 so large thatThen we can know thatφ(·,·,·,·)∈Contr(B0,Σ)for eachfixedT.

From the proof procedure of Theorem 4.1,we can deduce that for any fixedT,we have

is bounded inH1and the bound depend onT.

Let(un,unt,φn,φnt,θn)be the solutions corresponding to initial dataB0with respect to symbolFn∈Σ,n=1,2,···.Then from(4.4),we can infer

Hence from(4.22)～(4.23),we concludeφ(·,·,·,·)∈Contr(B0,Σ)immediately.

Theorem 6Assume thatf,g,hsatisfy(4.4)and Σ is defined by(4.7),then the family of semi-processes{UF(t,τ)}(F∈Σ,t≥τ,τ≥0)corresponding to(4.1)has a compact uniform(w.r.t.F∈Σ)attractorAΣ.

ProofTheorem 4 and Theorem 5 imply the existence of a uniform attractor immediately.

§5.Semilinear Problems

In this section,we shall consider the following system

In order to obtain our results,we need Theorem 2.5.1,Corollary 2.5.1,Theorem 2.5.2,Definition 2.5.1,Theorem 2.5.4～Theorem 2.5.5 from the book[20].Thus we have the following results.

Moreover,there is an alternative,

ProofSame as the proof of Theorem 7,we haveH,D(A)andFis a nonlinear operator fromHintoH,F∈C1(H,H).Then we shall prove thatFsatisfies the local Lipschitz condition,in fact,for allU1=(u1,v1,φ1,e1,θ1),U2=(u2,v2,φ2,e2,θ2)∈H,‖U1‖H≤R,‖U2‖H≤R,whereRis an arbitrarily positive constant.

Then we get

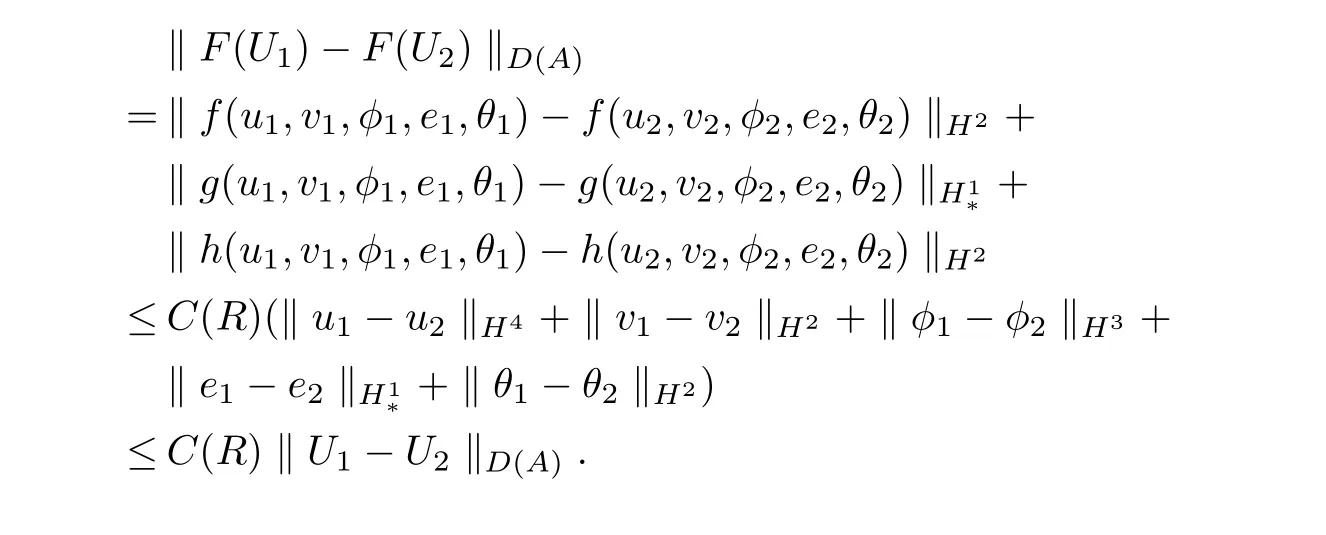
Thus,we use the Theorem 2.5.4～Theorem 2.5.5 in book[20]to complete the proof.

[1]BRULIN O,HYALMARSS S.Linear grade consistent micropolar theory[J].Int J Engng Sci,1981,19:1731-1738.

[2]CASAS P,QUINTANILLA R.Exponential decay in one-dimensional porous-thermoelasticity[J].Mech Res Comm,2005,32:652-658.

[3]CHEPYZHOV V V,VISHIK M I.Attractors of Equations of Mathematical Physics[C].Rhode Island:American Mathematical Society,2002.

[4]DUCOMET B.Simplified models of quantum fluids in nuclear physics[J].Proc Partial Differential Equations and Applications,Math Bohem,2001,126:323-336.

[5]LIU Zhuang-yi,ZHENG Song-mu.Semigroups Associated with Dissipative Systems[M].Boca Rat on FL:Chapman Hall CRC,1991.

[6]MESSAOUDI S A,SAID-HOUARI B.Energy decay in a Timoshenko-type system of thermoelasticity of type III[J].J Math Anal Appl,2008,348(1):298-307.

[7]PAZY A.Semigroups of Linear Operators and Applications to Partial Differential Equations[M].New York:Springe-Verlag,1983.

[8]QIN Yu-ming.Asymptotic behaviour for global smooth solutions to a one-dimensional nonlinear thermoviscoelastic system[J].J Partial Differ Equ,1999,12:111-134.

[9]QIN Yu-ming.Global existence and asymptotic behavior of solution to the system in one dimensional nonlinear thermoviscoelasticity[J].Quart Appl Math,2001,59:113-142.

[10]QIN Yu-ming.Exponential stability and maximal attractors for a one-dimensional nonlinear thermoviscoelasticity[J].IMA J Appl Math,2005,70:1-18.

[11]QIN Yu-ming.Nonlinear Parabolic-Hyperbolic Coupled Systems and Their Attractors,Operator theory[M].Basel-Boston-Berlin:Birkhauser,2008.

[12]QIN Yu-ming,HUANG Lan.Global well-Posedness of Nonlinear Parabolic-Hyperbolic Coupled Systems[M].Springer Basel AG,2012.

[13]QIN Yu-ming,LIU Xin,WANG Tai-ge.Global existence and uniqueness of nonlinear evolutionary fluid equations[M].Frontier in Mathematics,2015.

[14]QIN Yu-ming,WEI Tian-hui,REN Jia.Global existence,asymptotic behavior and uniform attractors for non-autonomous thermoelastic systems[J].Department of Applied Mathematics,2012,53(6):3106-3107.

[15]RYMARZ C.On the model of non-simple medium with rotational degrees of freedom[J].Bull Acad Polon Sci,S´er.Sci Techn,1968,16:272-280.

[16]TOUPIN R.A.Elastic materials with couple-stress[J].Arch Ration Mech Anal,1962,11:385-414.

[17]TOUPIN R.A.Theories of elasticity with couple-stress[J].Arch Ration Mech Anal,1964,17:85-112.

[18]WATSON S.J.Unique global solvability for initial-boundary value problems in one dimensional nonlinear thermoviscoelasticity[J].Arch Rat Mech Anal,2000,153:1-37.

[19]WU Zhong-lin,XU Juan-juan.Global existence inH2for a one-dimensional non-monotone fluid[J].Chin Quart J Math,2007,22:296-304.

[20]ZHENG Song-mu.Nonlinear Evolution Equations.Pitman Monographs and Surveys in Pure Applied Mathematics[J].CRC,2004,133:46-58.

[21]ZHENG Song-mu,QIN Yu-ming.Universal attractors for the Navier-Stokes equations of compressible and heat conductive fliuds in bundled annular domains inRn[J].Arch Rat Mech Anal,2001,160:153-179.