On the Error Term for the Number of Solutions of Certain Congruences
2017-03-14
(School of Mathematics,Hefei University of Technology,Hefei 230009,China)
§1.Introduction
Letf(x)Suppose thatLis the splitting field offover Q with Galois groupG=Gal(L/Q).IfGis Abelian,we call the fieldLis Abelian and thatf(x)is an Abelian polynomial.Otherwise we callf(x)a non-Abelian polynomial.Letr(n)denote the number of solutionsxof the congruencef(x)≡0(modn)satisfying 0≤x<n.We introduce theL-function associated tor(n),

It is a classical problem to study the functionr(n).In 1952 Erdös[1]proved that

and the lower bound

It is hard to refine Erdös’result.Until 2001,Fomenko[2]proved the asymptotic formulae
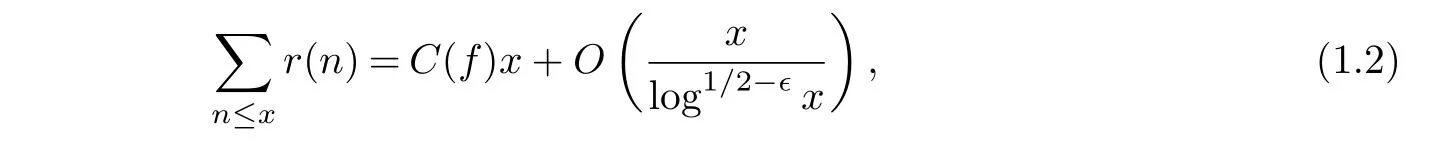
whereC(f)is a positive constant depending onf.
In[2],Fomenko also proved that for any Abelian polynomialf(x)of degreem,
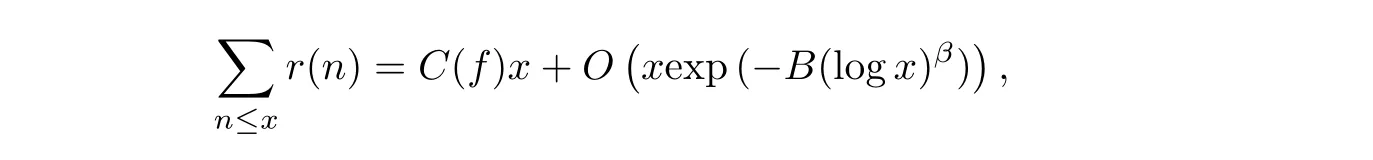
for a certain positive constantBand any fixedβ<.¡By introducing the¢Langlands functionality to this problem,Kim[6]improved the error termOxexp(−B(logx)β)intoO(x1−3/(m+3)+ε)for any fixedε>0.
In addition,in[6]it was shown that for any non-Abelian polynomialf(x)of degreem≥2,

whereαis the residue ofL(s)which is defined in(1.1)at its simple poles=1.Recently based on Kim’s method,LYU[7]improved Kim’s result and obtained the sharper error termO¡x1−3/(m+6)+ε¢.


Motivated by[2-4],the aim of the present paper is to investigate∆(x)in mean square and we shall prove the following theorem
Theorem 1Let∆(x)be defined in(1.3).For any non-Abelian polynomialf(x)of degreem≥2 and suppose thatm≥3.Then we have

In fact the proof shows that

form=2.
RemarkForm=2,3,the result of Theorem 1 is as good as that obtained under the Riemann Hypothesis on DirichletL-functions on average.
NotationsThe Vinogradov symbolA≪Bmeans thatBis positive and the ratioA/Bis bounded.The letterεan arbitrary small positive number,not the same at each occurrence.
§2.Proof of Theorem 1
To prove Theorem 1,we need the following lemmas.
Lemma 2.1LetKbe a Galois extension of degreenover Q andL(s)be defined in(1.1).Then we have

whereU(s)denotes a Dirichlet series,which is absolutely and uniformly convergent for Re(s)>andζ(s,K)denotes the Dedekind zeta function of the fieldK
ProofThis follows immediately by the arguments(see pages 319-320)in[7].
Lemma 2.2LetKbe an algebraic number field of degreem.Then for any fixedε>0
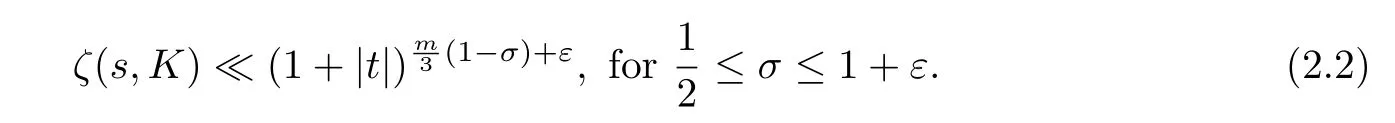
ProofBy Lemma 2.5 in[8]and the Phragmén-Lindelöf principle for a strip(see e.g.Theorem 5.53 in Iwaniec and Kowalski[5],this lemma follows.
Now we begin to complete the proof of Theorem 1.By the definition ofr(n),we have
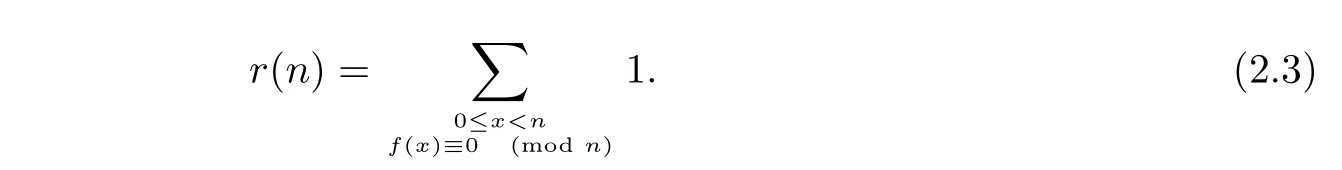
From Lemma 3 in[1],it is known that the functionr(n)is multiplicative and satisfies
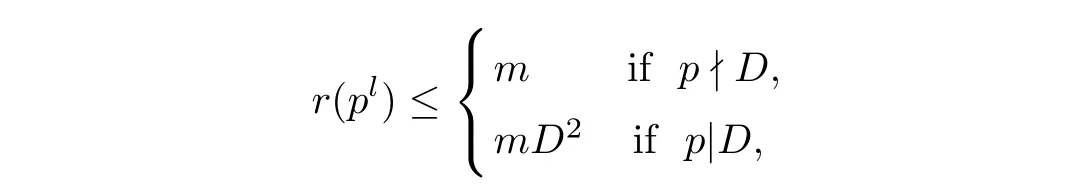
for natural numberl>0,whereDis the discriminant off(x).Then we have
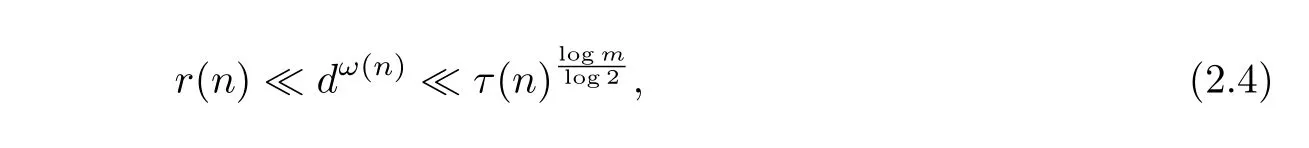
whereω(n)denotes the number of distinct prime divisors ofnandτ(n)is the divisor function.
Let

From(2.4),(1.1)and Perron’s formula(see Proposition 5.54 in[5]),we get

By the propertyL(s)only has a simple pole ats=1 for>and Cauchy’s residue theorem,we have

Then in order to prove(1.4)in Theorem 1,we shall prove the following results.
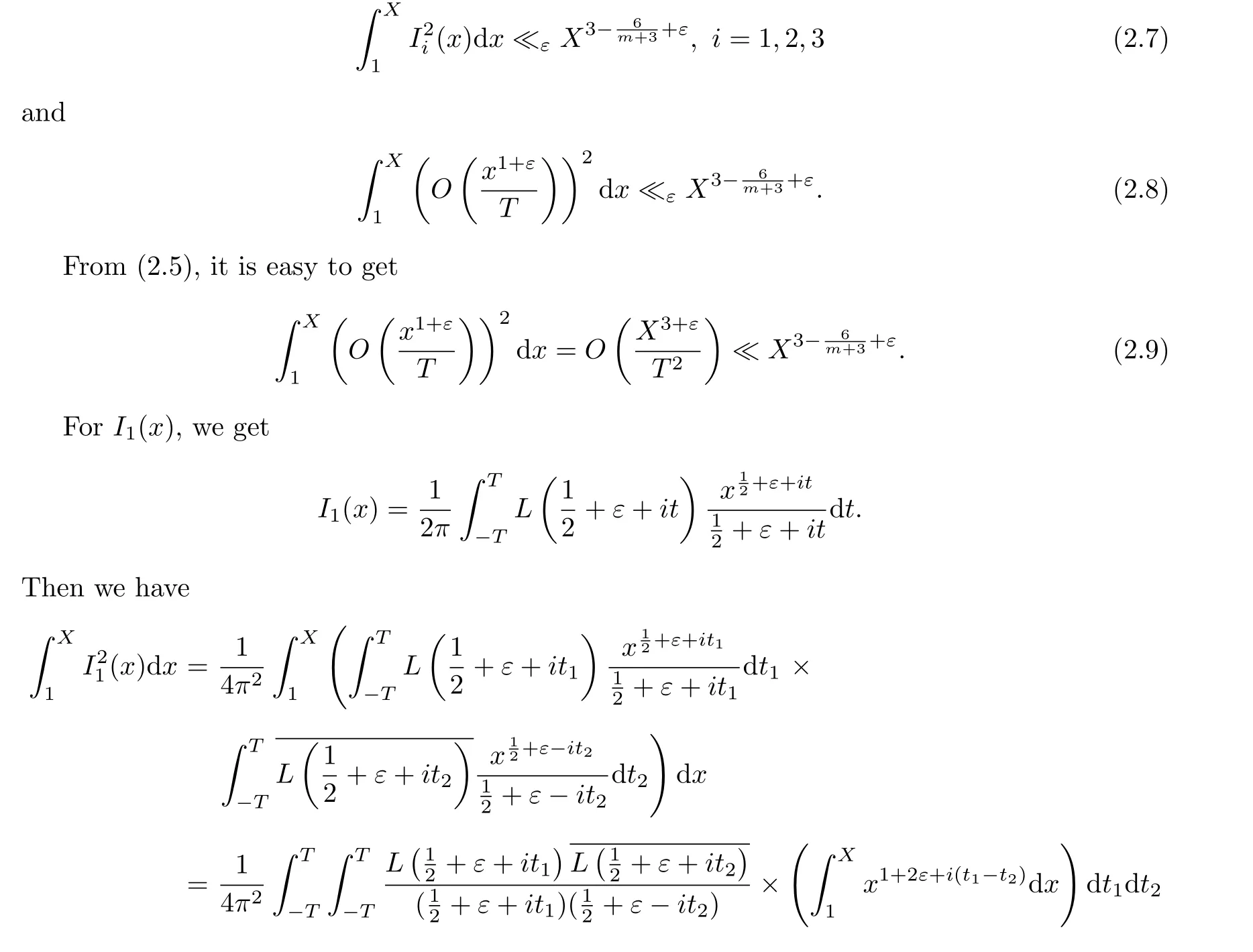
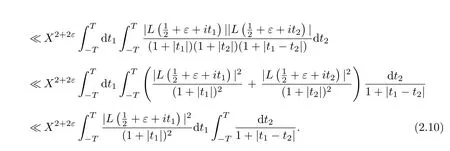
To go further,we get
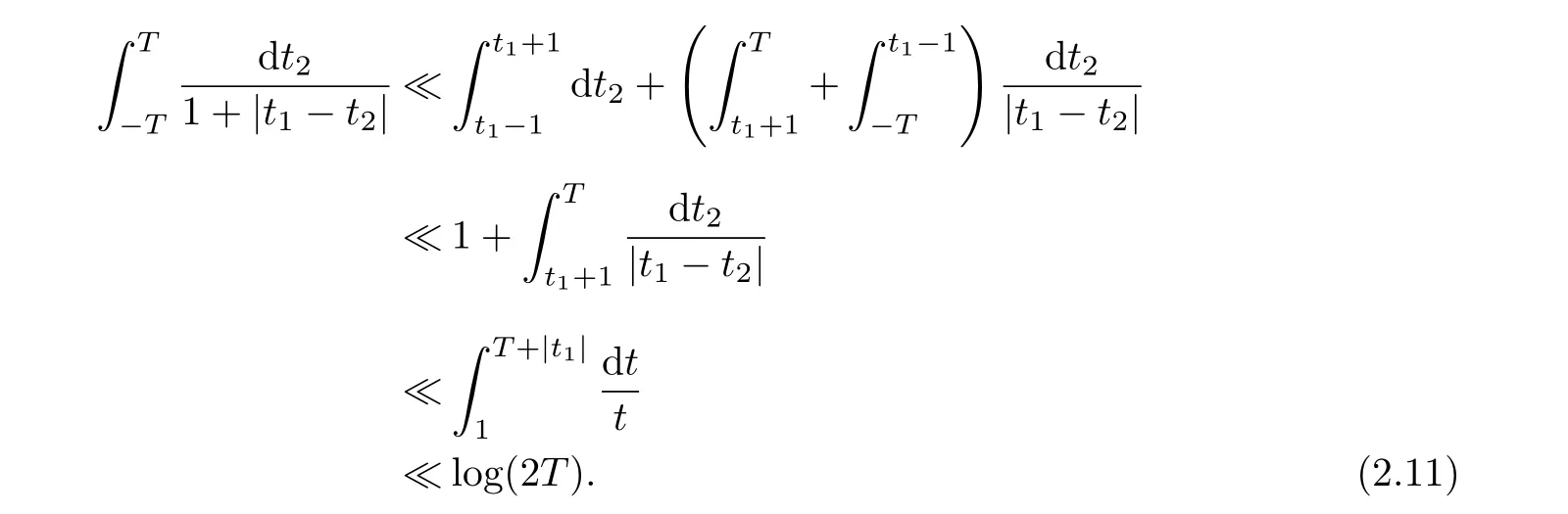
By(2.10)~(2.11)and(2.1),

where we have used lemmas 2.1 and 2.2.
By Lemma 2.2,we have

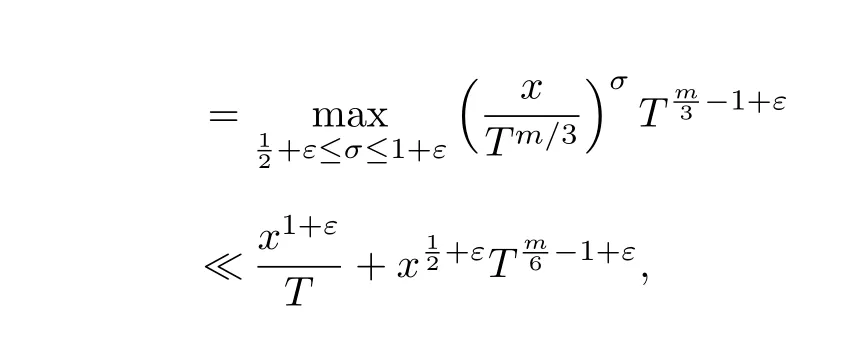
which yields
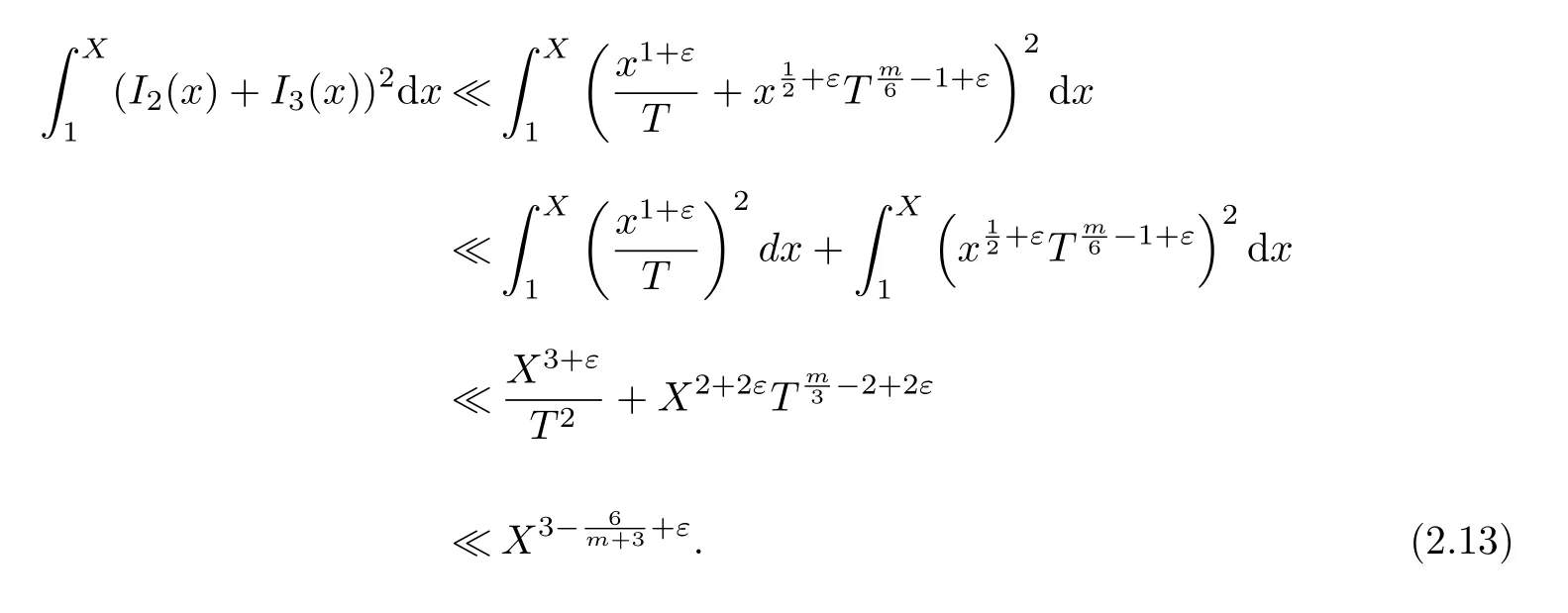
The inequalities(2.7)~(2.8)immediately follow from(2.9),(2.12)~(2.13).That is,we have
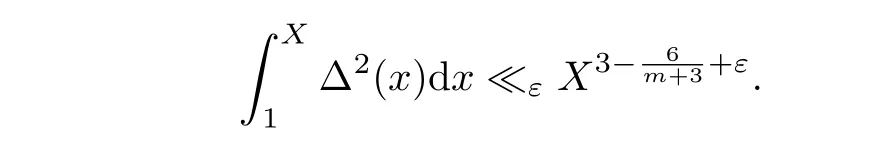
Form=2,by takingT=,the detail of the proof of(1.5)is similar to that of(1.4),hence we omit it here.Then the proof of Theorem 1 is completed.
[1]Erdös P.On the sum J London Math,Soc,1952,27:7-15.
[2]FOMENKO O M.The mean number of solutions of certain congruences[J].J Math Sci,2001,105:2257-2268.
[5]IWANIEC H,KOWALSKI E.Analytic number theory[J].Amer Math Soc Colloq Publ,2004,53:204-216.
[6]KIM H H.Functoriality and number of solutions of congruences[J].Acta Arith,2007,128:235-243.
[7]LYU G.Number of solutions of certain congruences[J].Acta Arith,2009,140:317-328.
[8]LYU G,YANG Z.The average behavior of the coefficients of Dedekind zeta function over square numbers[J].J Number Theory,2011,131:1924-1938.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Sub-harmonic Resonance Solutions of Generalized Strongly Nonlinear Van der Pol Equation with Parametric and External Excitations
- Global Existence,Asymptotic Behavior and Uniform Attractors for Damped Timoshenko Systems
- The Representation Problems of Conjugate Spaces of l0({Xi})Type F-normed Spaces
- Convergence Rates for Elliptic Homogenization Problems in Two-dimensional Domain
- Applications of¢-expansion Method in Solving Nonlinear Fractional Differential Equations
- On Rings with Finite Global Gorenstein Dimensions
