Applications of¢-expansion Method in Solving Nonlinear Fractional Differential Equations
2017-03-14
(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China)
§1.Introduction
Due to the availability of symbolic manipulation programs,considerable work has been done on investigating exact solutions of nonlinear differential equations(NLDEs)of integer order such as the trigonometric function series method[1],the modified mapping method and the extended mapping method[2]and others.The nonlinear fractional differential equations(NLFDEs)considered as the generalization form of NLDEs of integer order describe various important phenomena in physics,fluid dynamics,engineering,material science and so on.Recent past,the fractional complex transformation[3]has been suggested to convert a nonlinear fractional differential equation with Jumarie’s modification of Riemann-Liouville derivative into its classical differential partner.The motivation of this article is to use the-expansion method[4]together with the fractional complex transformation to search for exact solutions of time-fractional Burgers equation and space-fractional coupled Konopelchenko-Dubrovsky equations by virtue of symbolic computation.
For readability,we briefly recall the Jumarie’s modified Riemann-Liouville derivative[5]of orderα,i.e.,

And modified Riemann-Liouville derivative possesses the following properties
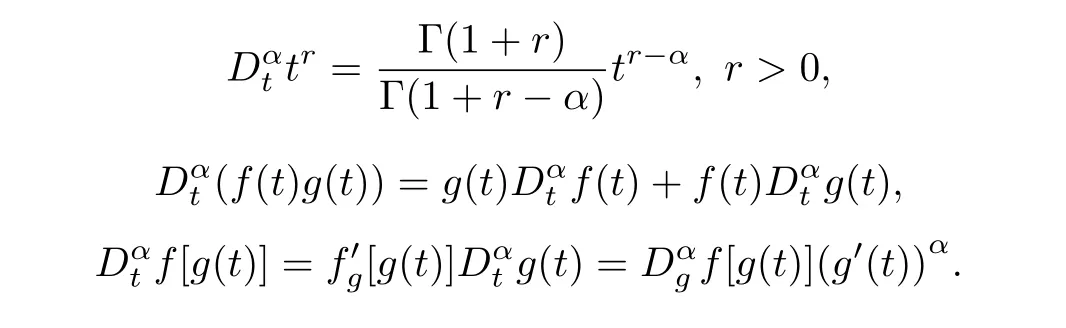
The plan of this paper is as follows.In Section 2,we give a detailed description of the-expansion method involving the fractional complex transformation.In Section 3,timefractional Burgers equation and space-fractional coupled Konopelchenko-Dubrovsky equations are computed to obtain many families of exact solutions.A short summary is given in last section.
§2.Description of Method
Here we intend to present the computational steps about the-expansion method.
Consider a nonlinear fractional differential equation given by

where dependent variableu=u(t,x,y).AndNis interpreted as a polynomial inuand its fractional derivatives.
First,taking a transformation as
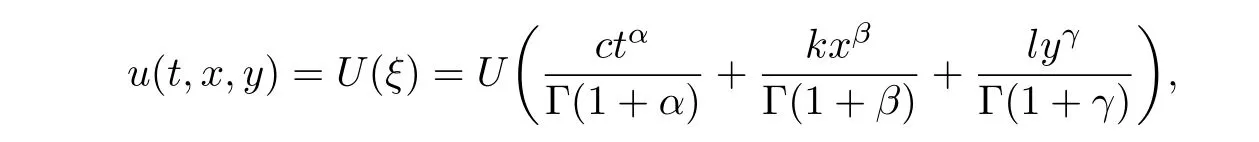
wherec,k,lare undetermined constants,one can convert Eq(2.1)into an ODE
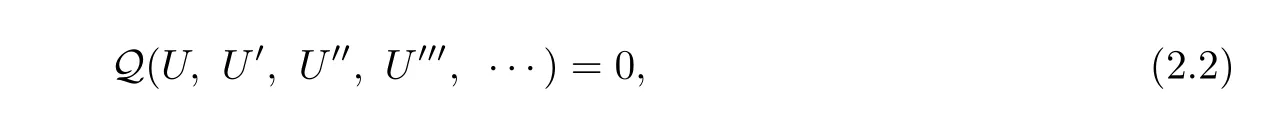
where the superscript′denotes the derivative with respect toξ.
Second,we suppose that Eq(2.2)admits formal solution in the form

whereG=G(ξ)is a solution of

withµ/=1 andλ/=0 being integers.In(2.3),a0,ai,bi(i=1,2,···,m)are constants to be determined.Through the balance relation between highest order derivative and nonlinear terms appearing in Eq(2.2),it is easy to reveal the value of positive integerm.
Third,with the aid of symbolic computation software,expression(2.3)into(2.2)and using(2.4),collecting all terms with the same powers of(j=0,±1,±2,···)and setting the coefficients of terms(j=0,±1,±2,···)to zero,one can get a set of nonlinear algebraic equations with respect to unknowns.Calculating these equations by symbolic computation software,the solutions are then derived.
Fourth,on basis of the general solutions to Eq(2.4),the ratiocan be divided into three cases.

whereAandBare nonzero constants.Putting the values ofa0,ai,bi(i=1,2,···,m)and the ratios(2.5)~(2.7)into(2.3)yields three types of solutions for Eq(2.1).In contrast with the methods in[6-7],the expansion method leads to some different hyperbolic function solutions due to its difference of hyperbolic function solution for equation(2.4).
§3.Applications
In this section,two specific fractional differential equations will be calculated.We begin with the time-fractional Burgers equation.
3.1 Time-fractional Burgers Equation
The time-fractional Burgers equation[8]reads

whereαis a parameter describing the order of the fractional time derivative.
By the transformation
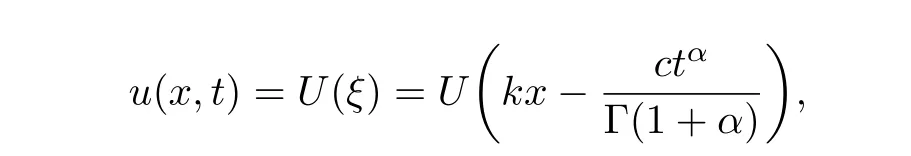
Eq(3.1)is reduced to
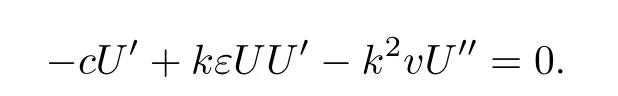
And then integrating once with respect toξ,we have

withC0being an integration constant.BalancingU′andU2in Eq(3.2)determinesm=1,hence the formal solution(2.3)can be written as

wherea0,a1andb1are three unknownSubstituting(3.3)along with equation(2.4)into(3.2),then extracting the coefficients of all(j=0,±1,±2),five algebraic equations aboutc,k,v,ε,a0,a1,b1,C0are directly obtained as

Combining the three cases with(3.3)and inserting ratios(2.5)~(2.7),there exist three groups of solutions for Eq(3.1)as follows
Family 1Whenµλ>0,the expression of the trigonometric function solution reads

whereξ=
3.2 Space-fractional Coupled Konopelchenko-Dubrovsky Equations
Next we focus on the space-fractional coupled Konopelchenko-Dubrovsky equations[9]

where 0<α,β,γ≤1.The equations are a variation of the coupled Konopelchenko-Dubrovsky equations of integer order.
Applying the transformations
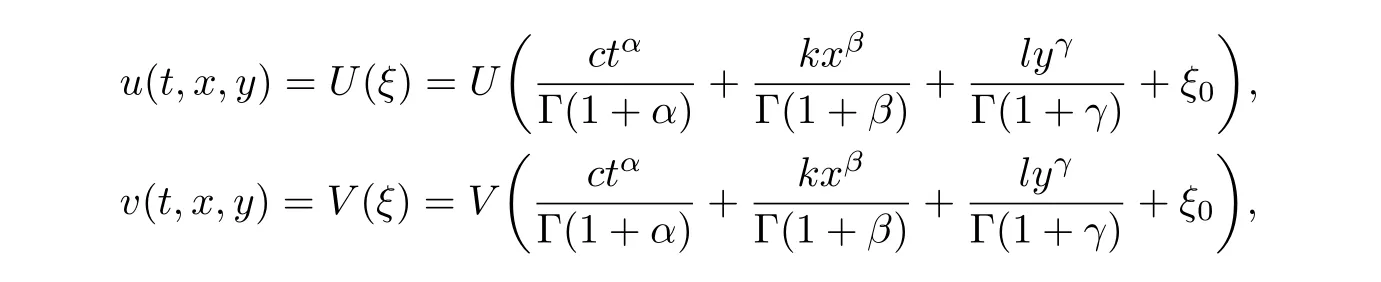
to the original equations(3.4),one gets
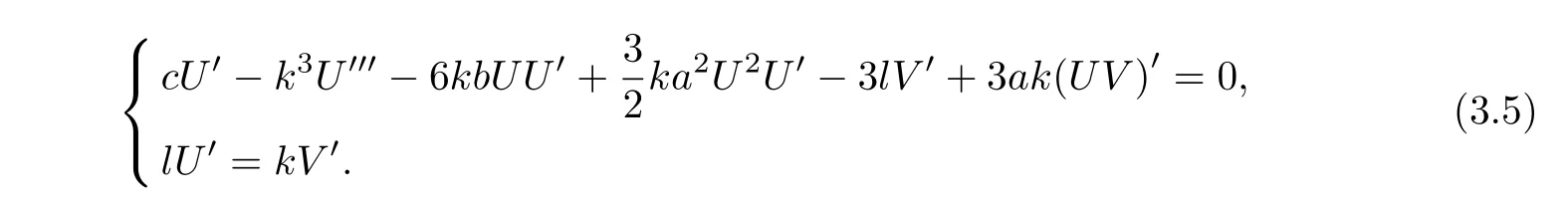
Analyzing the highest order derivative and nonlinear terms in(3.5)yields

wherea0,a1,b1,α0,α1andβ1are constants to be determined later.Proceeding similar computations as the previous example,a series of algebraic equations derived from the coefficients(j=0,±1,±2,±3,±4)are given by

The solutions that follow these equations are

Substituting the four cases along with(2.5)~(2.7)into expression(3.6),we arrive at
Family 1Corresponding to Case 1,ifµλ>0,the exact solutions in terms of trigonometric function can be written as
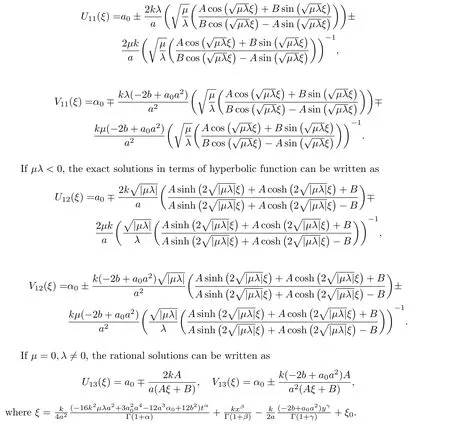
Family 2Corresponding to Case 2,ifµλ>0,the exact solutions in terms of trigonometric function can be written as


Family 3Corresponding to Case 3,ifµλ>0,the exact solutions in terms of trigonometric function can be written as


§4.Conclusion
In summary,we have successfully extended the¢-expansion method for seeking exact solutions of NLFDEs.The validity and power for this method have been tested via solving time-fractional Burgers equation and space-fractional coupled Konopelchenko-Dubrovsky equations.Consequently,a series of exact solutions that include several free constants for them are obtained.A number of NLFDEs arising in various fields can be considered by this method.
[1]ZHANG Zai-yun.New exact traveling wave solutions for the nonlinear Klein-Gordon equation[J].Turkish Journal of Physics,2008,32:235-240.
[2]ZHANG Zai-yun,LIU Zhen-hai,MIAO Xiu-jin,et al.New exact solutions to the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J].Applied Mathematics and Computation,2010,216:3064-3072.
[3]LI Zheng-biao,HE Ji-huan.Fractional complex transform for fractional differential equations[J].Mathematical and Computational Applications,2010,15(5):970-973.
[4]KANG Zhou-zheng.(G′/G2)-expansion solutions to MBBM and OBBM equations[J].Journal of Partial Differential Equations,2015,28(2):158-166.
[5]JUMARIE G.Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results[J].Computers and Mathematics with Applications,2006,51(9-10):1367-1376.
[6]MIAO Xiu-jin,ZHANG Zai-yun.The modified(G′/G)-expansion method and traveling wave solutions of nonlinear the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J].Communications in Nonlinear Science and Numerical Simulation,2011,16:4259-4267.
[7]ZHANG Zai-yun,HUANG Jian-hua,ZHONG Juan,et al.The extended(G′/G)-expansion method and travelling wave solutions for the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J].Pramana-journal of physics,2014,82(6):1011-1029.
[8]BEKIR Ahmet,GüNERözkan.Exact solutions of nonlinear fractional differential equations by(G′/G)-expansion method[J].Chinese Physics B,2013,22(11):110202.
[9]ZHENG Bin,FENG Qing-hua.The Jacobi elliptic equation method for solving fractional partial differential equations[J].Abstract and Applied Analysis,2014,2014:249071.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Sub-harmonic Resonance Solutions of Generalized Strongly Nonlinear Van der Pol Equation with Parametric and External Excitations
- Global Existence,Asymptotic Behavior and Uniform Attractors for Damped Timoshenko Systems
- The Representation Problems of Conjugate Spaces of l0({Xi})Type F-normed Spaces
- Convergence Rates for Elliptic Homogenization Problems in Two-dimensional Domain
- On the Error Term for the Number of Solutions of Certain Congruences
- On Rings with Finite Global Gorenstein Dimensions
