闽北湿地松人工林立地质量精确评价

倪伟星

（福建省武夷山市林业局，福建 武夷山 354300）

对于人工林起源林分来说，由于年龄结构较天然林简单，且受正常的抚育间伐的影响而不适合应用地位级表评价立地，取而代之的是地位指数。地位指数表是依据林分优势高与年龄的关系，用基准年龄时林分优势高的绝对值作为划分林地生产力等级的一种数表，它可分为多形和同形二种类型[1]，其中由于同形地位指数曲线人为地掩盖了不同林地上优势高林木生长规律的差异，从而影响了实际应用效果[2]。为了客观地反映人工林不同立地条件下优势高的生长规律，提高地位指数的预估精度，本次将立地质量等级作为虚拟变量，研制地位指数曲线模型。

地位指数表只适用于有林地，其不能单独反映每一立地因子对林木生长的作用。而数量化地位指数表既能定量地测定立地因子对林木生长的综合效应[3-5]，又能定量地测定出每一个立地因子对林木生长的影响大小[6-8]，所以本次将编制数量化地位指数和地位指数两种林业数表，为有林地、无林地的立地评价提供依据。

湿地松于20世纪30年代从美国东部引入我国，由于其具有生长速度快、产松脂丰富、抗旱性强、材种出材好等优点，已成为闽北山丘陵地区的主要造林树种之一，而当前闽北地区湿地松林业数表许多方面都是空白，套用马尾松的林业数表，造成一定的误差，这种状况严重影响了林业生产实践，给科学经营管理湿地松带来了许多困难。因此，为能精确地掌握湿地松林分的数量、质量及立地情况，科学地经营管理好湿地松林分，有必要编制地位指数表和数量化地位指数表[9-10]。

1 研究材料

1.1 地位指数编表材料

在福建省南平延平区、政和县、武夷山等地选择人为干扰较少的湿地松，采集临时样地、固定样地以及伐区调查设计数据，样地面积为0.067 hm2，形状为矩形。共采集了不同年龄和立地质量等级的样地259块，其中立地质量等级包括肥沃、较肥沃、中等肥沃、瘠薄，固定样地测定次数2～5次，年龄范围为10～58 a。每块样地每木检尺的起测直径为5 cm，主要林分因子分布范围见表1。

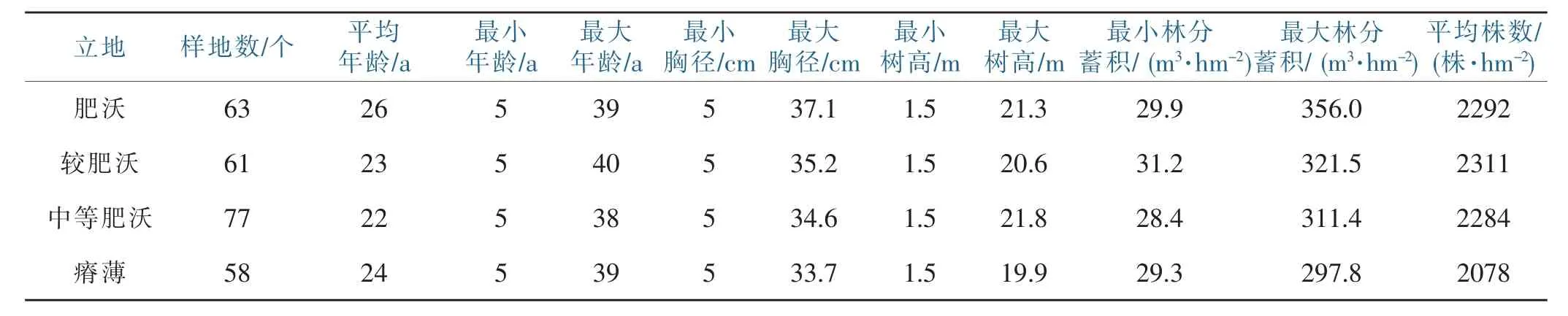
表1 样地数据采集概况Table 1 Survey of sampling data in sample plots

1.2 数量化地位指数表编制材料

共调查、收集了3个县（市）81块样地，每块样地包括坡向、坡位、坡度、坡形、海拔、质地、土壤厚度、土壤种类、土壤干湿度、土壤松紧度、腐殖质层厚度等11个因子，将所有样地的11个因子分别进行分级处理，共划分35个类目，具体见表2。

2 研究方法

2.1 地位指数模型的设计

由于理查德方程是适用性强、应用型最广的方程，同时能较好地描述林木年龄与优势高的生长规律，所以本次以该方程为基础方程，设计地位指数模型，方程一般形式见式（1）。

式中：a、b、c 为待求方程参数；Hu为林分优势高；t为林木年龄。

由于不同的立地条件，林地所提供的养分，环境因子的差异，湿地松生长规律也存在差异，为更精确地把握林分优势高生长规律，同时，为了研究结果便于在林业生产上应用，结合福建省森林资源清查中有关技术及林业生产实际情况，立地质量按四种等级划分，即肥沃（I1）、较肥沃（I2）、中等肥沃（I3）、瘠薄（I4）。结合理查德方程三参数的特性，将参数a、b、c作为I1、I2、I3、I4的函数，其参数公式见式（2）、（3）、（4）。

式中：a1、a2、a3、a4、b1、b2、b3、b4、c1、c2、c3、c4为待求参数。

根据理查德基础方程及参数方程，本次设计的湿地松地位指数曲线模型见式（5）。

表2 样地等级划分情况Table 2 Classification of plots

上式（5）是以理查德方程为基础模型，通过引入立地质量4个等级，构建了4个等级立地质量等级为虚拟变量、年龄为自变量、林分优势高为因变量的地位指数模型。虚拟变量的计算是将定性数据（立地质量等级）转化为定量数据，本次取0或者1值，所以虚拟变量的取值规则为：当立地质量为某一等级时，该等级取值为1；其它等级取值为0。

根据虚拟变量的取值规律，最小二乘法无法求解式（5）的参数，因此需采用智能算法，如遗传算法、粒子算法、蚁群算法、模因算法、蛙跳算法等，通过这些算法的优缺点分析，同时能更精确地得到模型参数，本次采用在解决优化问题方面具有更快搜索速度的蛙跳算法，该方法具有更高成功率和更快收敛速度，为精确地评价立地质量提供参数。

蛙跳算法估计模型参数的步骤一共3步，第1步子群划分，第2步子群内部搜索，第3步全局信息交换。其中子群划分的步骤为：设候选解为n，子群数为k，用表示第个候选解，D为n的维数，那么对于随机产生的初始解按适应度降序排序后，候选解X1分入K1，X2分入 K2，X2分入 K2，… ，依次将所有候选解按适应度分配完毕。子群内部搜索的步骤为：所有候选解中适应度最佳的设为Xm，其中一个ki中适应度最佳的为Xb，最劣为Xw，那么子群内部搜索可按计算，其中X'是产生的新解，R为随机数（0,1,2,3,…,10），通过计算，若X'比Xw更优，则，若Xw更优，则，通过重复计算，搜索策略，直至搜索次数大于最大子群内部搜索次数，如果在执行搜索策略过程中，X'一直比Xw劣，则应随机产生另一个解，取代最佳适应度Xb。最后1步中，全局信息交换是在所有子群内部更新都完成的基础上，通过第1、2步进行重新执行，直到得到最佳结果。

2.2 数量化理论I

由于无林地立地质量评价指标多为定性数据，因此本次采用数量化理论I研编湿地松数量化地位指数表，该方法与其他多元统计回归分析相比，既能处理定性数据，又能进行定量分析。其模型为：

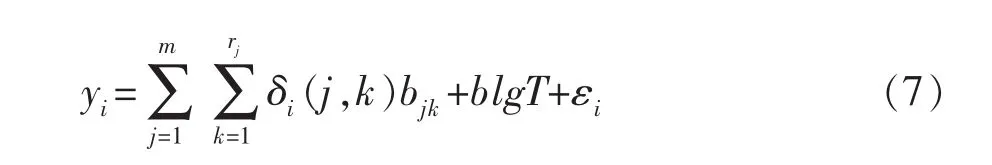
式中：i为样地号，取值为 1,2,…… n；j为项目数，取值为 1,2,… … m ；k 为类目数，取值为 1,2,… … rj，；bjk是第j个项目第k个类目中的得分值；b为待定参数，林分年龄的得分值；T为林分年龄；εi为随机误差；yi为第i个标准地的优势高。

3 研究结果

3.1 地位指数模型设计估计结果

利用肥沃、较肥沃、中等肥沃、瘠薄四类立地质量的样地材料，根据蛙跳算法估计模型参数的步骤求解a1、a2、a3、a4、b1、b2、b3、b4、c1、c2、c3、c4参数。拟合的相关指数为0.976，说明拟合效果较好。各参数拟合情况见表3。

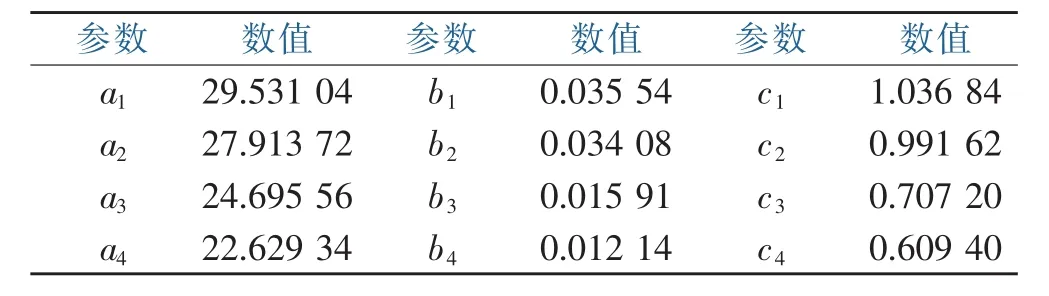
表3 地位指数导向曲线拟合结果Table 3 Position index orientation curve fitting result

将未参加建模的样本材料进行适用性检验。通过检验，其平均系统误差为2.846%，平均相对误差绝对值为7.523%，说明该模型预测精度较高，可用于湿地松林分立地质量评价及地位指数表的编制。

3.2 地位指数表的编制

地位指数表的编制方法有标准差、变动系数调准法，本次以导向曲线为基础，按基准年龄时树高值和指数级距，采用标准差法，编制湿地松地位指数表。利用该方法应建立林分年龄与对应优势树高的标准差方程。根据收集的解析木数据，通过多个方程对比，得到拟合较好方程为倒数方程。同样，为了与地位指数模型相对应，对参数a、b作为立地质量等级的函数，建立基于立地质量等级为虚拟变量的湿地松优势树高标准差模型，所以构建的模型为：

式中：S 为优势树高标准差；t为年龄；a1、a2、a3、a4、b1、b2、b3、b4为待求参数。

上述所建的模型同样通过蛙跳算法求解其参数，根据收集的基础数据，得到模型参数见表4。

表4 优势树高标准差模型参数计算结果Table 4 Calculation results ofmodel parameters of dominant tree height standard deviation

通过智能算法估计湿地松平均树高标准差方程参数，其相关指数0.964，说明本研究拟合的方程精度较高。将未参与建模的数据带入方程中，利用平均系统误差和平均相对误差绝对值两个指标评价模型实用性。通过检验，平均系统误差2.647%，平均相对误差绝对值7.556%，剩余标准差3.245，预估精度92%，说明模型适用。

当立地质量等级为肥沃时，设定基准年龄为20年，根据标准差调准法的编表步骤，利用拟合导向曲线和优势高标准差方程即可编制的湿地松地位指数表，具体见表5。

3.3 数量化地位指数表的编制

以样地6株优势木的平均高作为基准变量（yHu），将坡向、坡位、坡度、坡形、海拔、质地、土壤厚度、土壤种类、土壤干湿度、土壤松紧度、腐殖质层厚度等11个立地因子和林分年龄作为说明变量（xi），分别树种列出反应表。

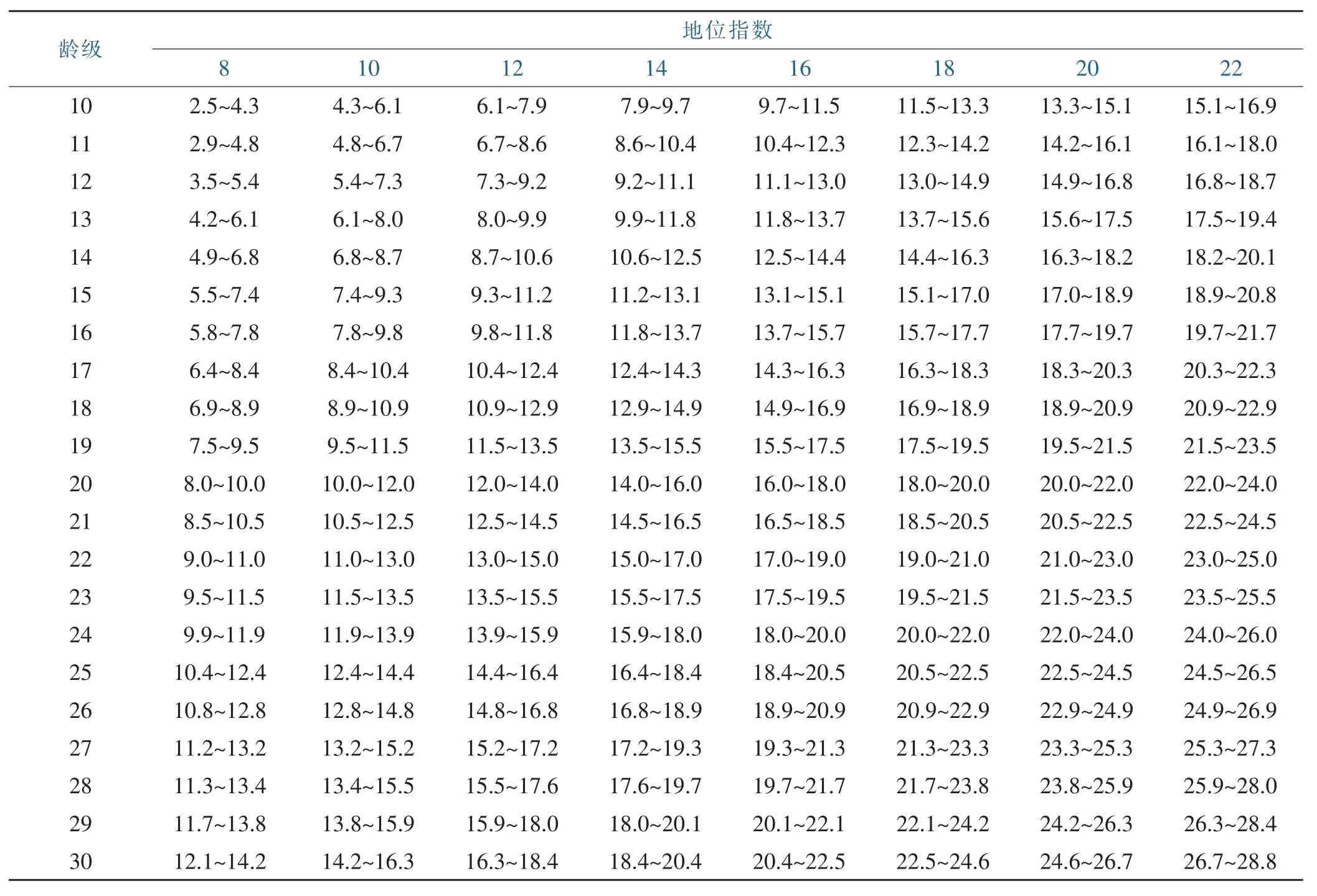
表5 立地质量等级为肥沃的湿地松地位数表Table 5 Pinus elliottii status table under fertile of site quality grade

根据数量化理论I的计算模型，在计算机上运算，得到各项目的得分值、偏相关系数、T检验值及模型的复相关系数，并对各相关系数进行t检验，其结果见表6。

由表6可知，影响湿地松林分优势高生长的主要项目有：坡位、坡形、海拔、质地、土壤厚度、土壤松紧度、腐殖质层厚度、年龄。根据数量化理论I模型，各立地因子相对不发生变化，那么由各立地因子所引起的树木增长是一定的，其其余的高生长均是由年龄所致。因此，将不同年龄的得分值与各项目中有关类目的得分值相加，即可知数量化优势高随年龄变化的情形，详见表7。

表6 各项目偏相关系数、t检验值结果及得分值Table 6 Partial correlation coefficient,t test resultand score value of each item

表7 湿地松数量化地位指数Table 7 Quantification standing index of Pinus elliottii

3.4 立地类型的划分及立地质量评价

为了便于评价无林地的立地质量，我们在表7的基础上，将各类目得分值代数和的极差（最大代数和减最小代数和）三等分，将其值由最大到最小组合为4个数值范围，也即为4个立地类型（Ⅰ、Ⅱ、Ⅲ、Ⅳ），从而编制了数量化立地质量评价表，详见表8。

表8 湿地松数量化立地质量评价表（基准年龄20年）Table 8 Quantitative site quality evaluation of Pinus elliottii(base age 20 years)

从表8可以看出，Ⅰ类地和Ⅳ类地上林木的生长量差异悬殊，说明湿地松对立地要求较为敏感。因此培育大径材应选择Ⅰ类地，培育中小径材应选择Ⅱ类地，在Ⅲ类地上可考虑营造混交林。根据相关因子的分析，湿地松造林选择宜林地时，要特别注意坡位、坡形、海拔、质地、土壤厚度、土壤松紧度、腐殖质层厚度等主要因子的选择。

4 结论与讨论

基于人工林受正常的抚育间伐的影响而不适合应用地位级表评价立地，取而代之的是地位指数。以理查德方程为基础方程，引入立地质量等级，构建了以林分年龄为自变量、立地质量等级为虚拟变量的湿地松地位指数模型。根据虚拟变量的取值特点，选用蛙跳算法求解地位指数曲线模型参数。将未参加建模的数据进行适用性检验，通过检验，平均系统误差为2.042%，平均相对误差绝对值为7.366%，模型预测精度较高，可用于湿地松立地质量评价。最后根据标准差法编表思路，建立了的湿地松优势树高标准差模型，编制了湿地松地位指数表。

考虑到湿地松地位指数表只适用于有林地，其不能单独反映每一立地因子对林木生长的作用。而数量化地位指数表既能定量地测定立地因子对林木生长的综合效应，又能定量地测定出每一个立地因子对林木生长的影响大小，可直接用环境因子定量地估计宜林地的地位指数，评价林地生产潜力，编制湿地松数量化地位指数表为精准提升森林经营质量提供技术支持。

由于大口径样地数据量还是比较缺少，对拟合的湿地松地位指数模型有待进一步修正。在建模过程中，也未同时利用多种智能算法进行比较分析，只从成功率、收敛速度方面选取本次研究的算法。

[1]郭艳荣,吴保国,刘洋,等.立地质量评价研究进展[J].世界林业研究,2012(5):47-52.

[2]施恭明,江希钿,陈绍玲,等.福建省湿地松多形地位指数曲线模型的研究[J].林业勘察设计,2015(2):1-4.

[3]于玉芳,李静,刘东.昌宁县华山松数量化立地指数表编制[J].南方林业科学,2015(2):36-38.

[4]吴恒,党坤良,田相林,等.秦岭林区天然次生林与人工林立地质量评价[J].林业科学,2015(4):78-88.

[5]王超群.人工林立地质量评价系统的研建[D].北京:北京林业大学,2013.

[6]朱光玉,康立,何海梅,等.基于树高-年龄分级的杉木人工林多形立地指数曲线模型研究[J].中南林业科技大学学报,2017,37(7):18-29.

[7]李艳洁,周来,靳爱仙,等.东京城林业局落叶松人工林立地质量评价[J].林业资源管理,2017(2):53-57.

[8]徐罗,亢新刚,郭韦韦,等.天然云冷杉针阔混交林立地质量评价[J].北京林业大学学报,2016,38(5):11-22.

[9]华伟平,丘甜,江希钿,等.立地质量等级为哑变量的黄山松地位级指数模型的研制[J].武夷学院学报,2015,34(3):15-18.

[10]黄国胜,马炜,王雪军,等.基于一类清查数据的福建省立地质量评价技术[J].北京林业大学学报,2014,36(3):1-8.