基于自组织神经网络的滚动轴承状态评估方法
2017-03-14张全德欧阳文理滕春禹王洪伟
张全德 陈 果 林 桐 欧阳文理 滕春禹 王洪伟
1. 南京航空航天大学民航学院,南京, 2100162. 中航工业综合技术研究所基础研究室,北京, 1000283. 北京航空工程技术研究中心第六研究室,北京, 100076
基于自组织神经网络的滚动轴承状态评估方法
张全德1陈 果1林 桐1欧阳文理2滕春禹2王洪伟3
1. 南京航空航天大学民航学院,南京, 2100162. 中航工业综合技术研究所基础研究室,北京, 1000283. 北京航空工程技术研究中心第六研究室,北京, 100076
针对单一特征在进行故障诊断时准确率不高的问题,提出了一种基于自组织神经网络(SOM)的滚动轴承状态评估方法。该方法首先从原始振动信号中提取出多特征数据,运用主成分分析(PCA)方法对多特征数据进行预处理,采用SOM进行网络训练,构建多特征数据的融合模型,输出竞争神经元层的权值矢量;然后,计算每一个样本到竞争神经元层权值矢量的最小欧氏距离,输出最终的融合指标;最后,通过比较待检测样本与正常样本的最小欧氏距离的差异来判断轴承的状态。将该方法应用于滚动轴承状态评估,试验结果表明:融合指标比单一指标对早期故障更加敏感、更加稳健;同时,融合指标能够定量地描述轴承状态的劣化过程。
自组织神经网络;主成分分析;特征融合;最小匹配距离;滚动轴承;故障识别
0 引言
滚动轴承作为航空发动机的关键部件,其运行状态直接影响飞行安全。由于航空发动机在高速、高温、高压和重载等恶劣条件下运行,滚动轴承极易发生故障[1],因此,对航空发动机滚动轴承进行实时状态评估和健康监测具有重要意义。研究表明,单一特征难以实现滚动轴承状态的准确评估[2],因此,考虑利用多特征融合技术进行滚动轴承状态评估显得尤为重要。
古莹奎等[3]提出基于主成分分析(principalcomponentanalysis,PCA)和支持向量机(supportvectormachine,SVM)的齿轮箱故障特征融合分析方法,该方法不仅能降低特征维数和计算复杂度,而且能有效地提高故障诊断率。李凌均等[4]提出基于支持向量数据描述(SVDD)的特征融合方法,该方法只需要一类目标样本作为学习样本就可以建立起单值分类器,与传统的神经网络相比具有较好的分类能力和较高的计算效率。蒋全胜等[5]提出基于拉普拉斯特征映射的特征融合方法,利用拉普拉斯特征映射算法提取高维非线性数据中的低维流形特征进行故障诊断。张伟等[6]提出基于扩展局部线性嵌入算法(locallylinearembedding,LLE)的非线性系统特征融合故障诊断方法,为复杂非线性系统的故障诊断提供了一种新的有效方法。刘志川等[7]提出基于非线性降维算法和交互式遗传算法的特征融合方法,实现了对降维后数据的识别分类。袁宪锋等[8]提出多PCA模型及SVM-DS融合的故障诊断方法,与传统PCA模型的方法相比该方法有更高的正确率和稳定性。ZHANG等[9]提出混合威布尔-比例风险模型(mixtureWeibullproportionalhazardmodel,MWPHM),用来评估伴随多种失效模式的机械系统健康状态。YU[10]将高斯混合模型(Gaussianmixturemodels,GMM)应用于滚动轴承状态评估,取得了良好的效果。PAN等[11]基于改进的小波包分解和支持向量数据描述方法进行滚动轴承状态评估,并根据全局距离定义了一种有效的健康指标。汪瑾等[12]提出基于后验概率支持向量机的航空发动机滚动轴承状态评估方法,该方法将正常类和异常类滚动轴承样本进行后验概率支持向量机学习,根据后验概率支持向量机的后验概率输出结果进行轴承的状态评估。
本文提出了一种基于自组织神经网络(self-organizationmapping,SOM)最小匹配距离的多特征融合方法。该方法首先对原始振动信号进行特征提取,运用PCA对多特征数据进行预处理,再通过训练得出输出层神经元的权值矢量,然后计算测试样本的特征矢量与每一个输出神经元权值矢量欧氏距离的最小值,该距离即认为是特征矢量与最匹配竞争神经元层的距离[13-14]。最后根据最小匹配距离来判断滚动轴承的运行状态。实验结果表明,该特征融合能够很好地区分轴承的运行状态,大大提高状态评估精度。
1 自组织神经网络
1.1 自组织神经网络学习算法
自组织神经网络学习算法属于无监督竞争学习算法。自组织映射网络可以将任意维数的输入模式以拓扑有序的方式变换到一维或者二维的离散空间上,这种变换称为特征映射(feature mapping),用Φ表示,即Φ:输入空间H→输出空间A。其中,输入空间H是输入向量的集合,其维数等于输入向量的维数;输出空间A在二维网格的自组织映射中是二维的平面[15]。
自组织神经网络学习算法步骤如下:
(1)设置X(n)为输入向量,或称训练样本,X(n)=(x1(n),x2(n),…,xN(n))T;Wi(n)为权值矢量,Wi(n)=(wi1(n),wi2(n),…,wiN(n))T;i=1,2,…,M;迭代次数为K。
(2)初始化。将权值矢量Wi用小的随机值进行初始化;设置初始学习速率为η(0);对所有的输入向量X和权值矢量初始值Wi(0)进行归一化处理:
(1)
(2)
式中,‖Wi(0)‖、‖X‖分别为权值矢量和输入向量的欧氏范数。
(3)采样,近似匹配。从空间中选取训练样本X′,通过欧氏距离最小的标准
(3)
选取获胜神经元c,以实现神经元的竞争过程。
(4)更新。对获胜神经元拓扑邻域Nc(n)内的兴奋神经元,以Hebb学习规则
(4)
更新神经元的权值矢量,从而进行神经元的合作和更新过程。
(5) 更新学习速率η(n)及拓扑邻域,并对学习后的权值重新进行归一化处理:
(5)
(6)
(6)判断迭代次数n是否超过K;如果n≤K,就将n值增加1,转到步骤(3);否则结束迭代过程。
1.2 基于SOM最小匹配距离的特征融合算法
由于不同类型的特征包含了航空发动机滚动轴承在不同状态空间中的信息,因此对不同类型特征采取融合设计方法,进行融合诊断。首先使用PCA对多特征数据去其相关性;然后采用SOM网络训练获得获胜节点,对与获胜节点相连的权值进行调整,使其与输入矢量之间的差别越来越小,使训练后竞争网络的权值矢量能够代表输入矢量的特征[16];最终,计算测试样本到训练样本的权值矢量的欧氏距离,从而由多特征样本融合出一个距离特征量。诊断流程见图1。
融合的最小匹配距离d的计算公式如下:
d={minf1,minf2,…,minfj}
(7)

图1 特征融合的故障诊断流程Fig.1 The flowchart of fault diagnosis based on feature fusion
2 基于仿真数据方法验证及方法比较
2.1 仿真数据
使用仿真数据对其分类效果进行仿真验证。仿真数据选用圆分类数据,在直角平面oxy上的8×8矩形内随机产生868个样本,均匀分布在四个圆心在(0,0),半径依次为1、2、3、4的圆内,4组数据样本个数依次为49、192、192、435。仿真参数的信息如表1所示,仿真数据的二维平面散点图见图2。

表1 仿真数据基本信息

图2 仿真数据散点图Fig.2 The scatter plot of simulation data
2.2 后验概率支持向量机状态评估方法
标准支持向量机方法仅仅给出属于某类的判断,没有给出属于某类的概率;而滚动轴承状态评估则需要准确评估出滚动轴承当前所处的状态,即需要知道它属于正常或异常状态的概率,基于后验概率支持向量机正好满足了滚动轴承状态评估的需求[12],因此,选取后验概率支持向量机进行滚动轴承状态评估,结果如图3所示。
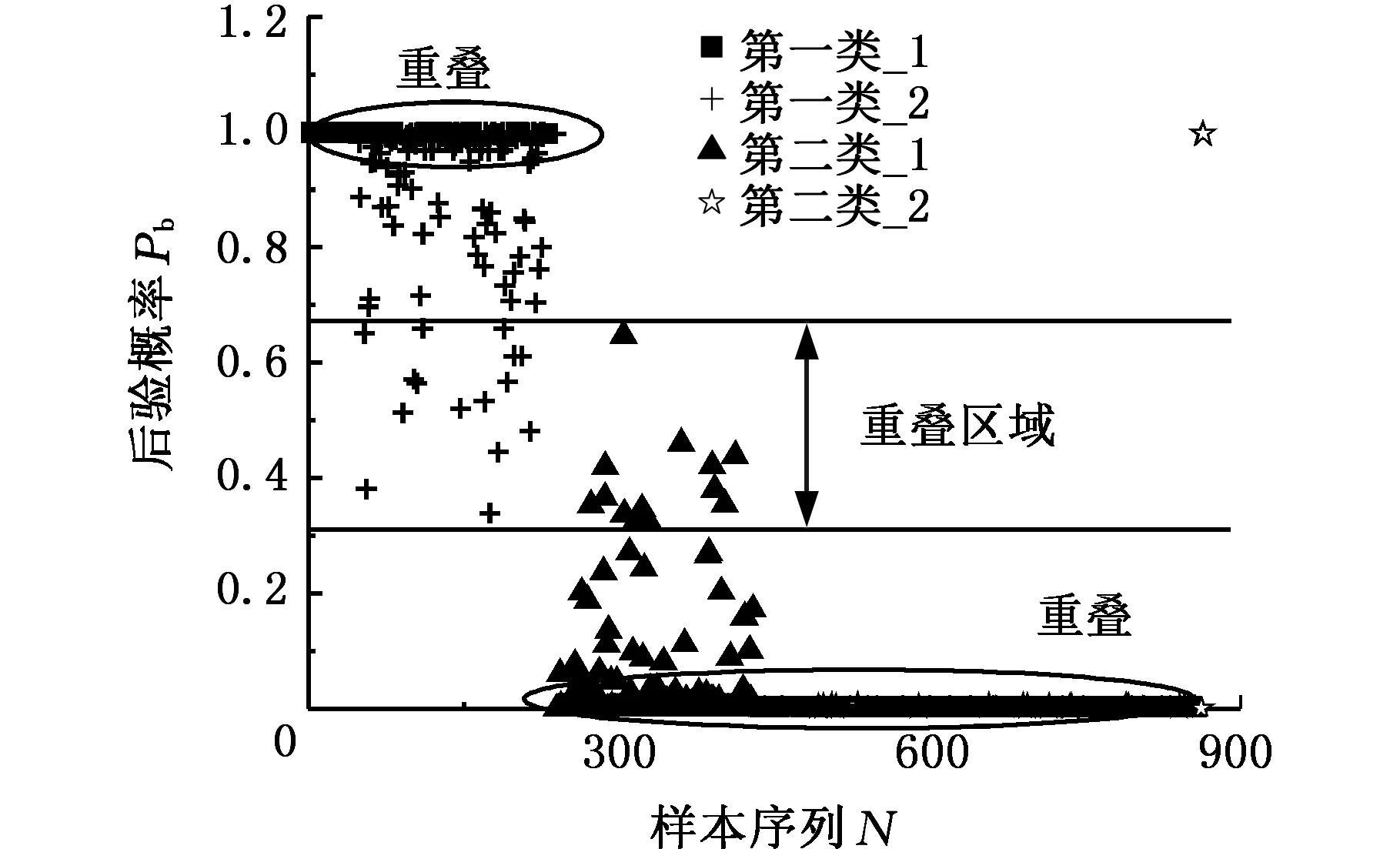
图3 后验概率支持向量机分类结果Fig.3 The classification results of posteriori probability SVM
由图3可知,两类数据几乎已经被完全分开。同类数据集距离决策面的远近不同,后验概率也明显不同,距离分类面较远数据集的后验概率大于距离分类面较近数据集的后验概率,从而实现了同类样本分类判断正确的可信度的区分。但是,由图3可知,后验概率支持向量机在进行状态评估时各类之间存在严重重叠,特别是第一类_2与第二类_1存在部分的重叠;并且第一类_1与第一类_2以及第二类_1与第二类_2在概率为1和0的地方重叠严重,因此无法对轴承各状态进行有效细致的区分。
2.3 基于SOM多特征融合状态评估方法
本文分别选取第一类_1、第二类_2为训练样本,其余类为测试样本分别借助SOM最小匹配距离算法进行融合诊断,结果如图4所示。
由图4可知,基于SOM最小匹配距离特征融合方法对仿真数据分类效果良好,能够将4种状态进行有效区分。尤其是经过特征融合后,融合后的特征量不仅能将各类样本分离开,而且也能够定量表达这4类样本之间的远近关系,这就意味着利用该融合方法得到的指标可以定量地描述设备状态的劣化过程。

(a)方案一:第一类_1为训练样本
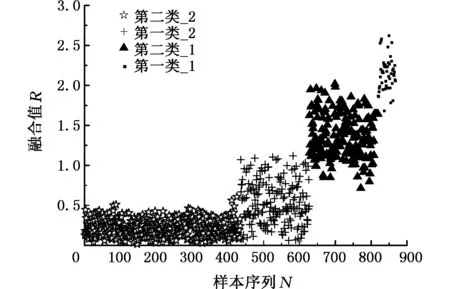
(b)方案二:第二类_2为训练样本图4 不同方案下的SOM融合结果散点图Fig.4 The scatter plots of SOM fusion results under different
3 基于试验数据的方法验证
3.1 滚动轴承故障试验
为验证所提出方法的有效性,采用沈阳发动机设计研究所(606所)研制的带机匣的航空发动机转子试验器进行故障识别试验[17],分别在试验器垂直上方和水平方向布置加速度传感器,获取机匣的振动加速度信号,试验轴承型号为6206型,轴承参数如表2所示,试验器如图5所示。
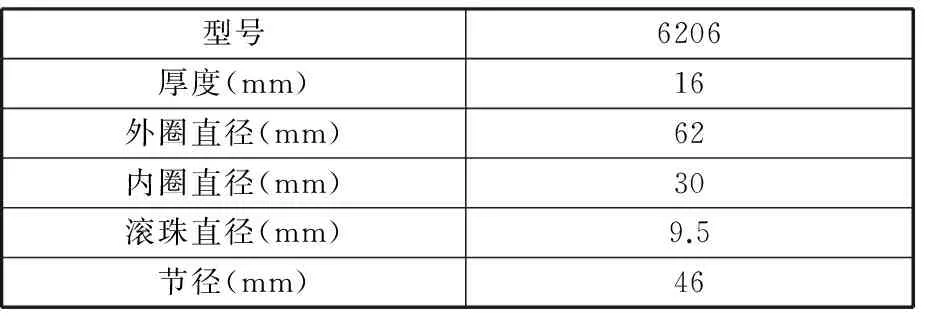
表2 6206型滚动轴承基本参数
采用线切割技术在航空发动机转子试验器涡轮机匣处的6206型号滚珠轴承上进行外圈故障、内圈故障和滚动体故障加工,如图6所示。分别在不同转速下进行了2组故障模拟试验(表3),每组试验数据包括正常、外圈故障、内圈故障、以及滚动体故障4种状态。

1.碰摩环 2.球轴承 3.涡轮盘 4.碰摩环点变形顶螺栓5.轴 6.滚柱轴承 7.压气机轮盘

图5 航空发动机转子试验器Fig.5 The rotor tester of aero-engine

(a)外圈故障 (b)内圈故障 (c)滚动体故障图6 故障加工后的6206型轴承Fig.6 6206 type bearing after fault processing

试验序号转速(r/min)测点11500机匣上方和水平方向21800机匣上方和水平方向
以转速为1500 r/min,机匣上方测点测得的振动加速度信号为例,提取12个量纲一特征的散点如图7所示。图中横坐标为样本序列,序列中1~110为正常状态样本,111~220为内圈故障样本,221~330为外圈故障样本,331~440为滚珠故障样本;纵坐标为各特征值。各特征数据如图7所示。
由图7可知,各特征均不能同时对轴承的三种故障都进行有效的识别以及区分,因此,考虑对多特征量进行融合,使之能够对正常状态和异常状态进行有效区分。

(a)歪度

(b)波形因数
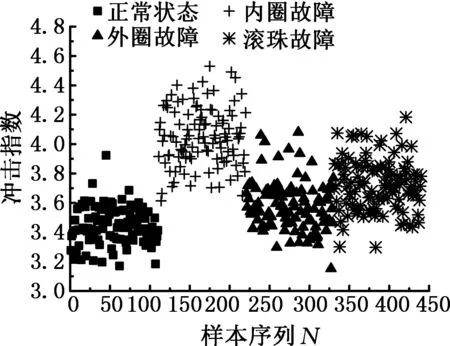
(c)冲击指数

(d)峰值指标

(e)峭度指标

(f)裕度指标

(g)重心频率

(h)均方频率
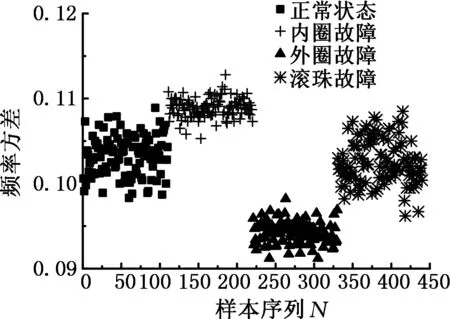
(i)频率方差

(j)内圈时频域特征量

(k)外圈时频域特征量

(l)滚珠时频域特征量
3.2 基于自组织神经网络的特征融合
采用自组织神经网络对该转子试验器的多特征数据进行融合,首先采用PCA对多特征数据进行去相关性,借助SOM最小匹配距离算法,得到神经网络的权值矢量,然后计算权值矢量与测试样本的最佳匹配距离,用该最佳匹配距离作为一个综合的劣化指标,对滚动轴承的运行状态进行评估,融合结果如图8所示。

图8 转子试验器SOM融合值Fig.8 The SOM fusion value of rotor tester
3.3 与其他融合方法的比较
将本文所提方法与支持向量数据描述(SVDD)以及一类分类支持向量机(one-class SVM)等特征融合方法进行比较,结果如图9、图10所示。

图9 转子试验器One-Class SVM融合值Fig.9 The fusion value of one-class SVM of rotor

图10 转子试验器SVDD融合值Fig.10 The fusion value of SVDD of rotor tester
由图8与图9、图10对比可知,SOM的识别结果明显好于SVM与SVDD的识别结果。为了定量描绘各方法融合前后故障识别率变化,以训练样本为基准计算单一特征和融合特征的识别率。识别率的算法步骤如下:
(1)选取正常样本的一部分进行训练,并以该训练样本为基准进行故障识别率的计算。记xij(i=1,2,…,n;j=1,2,…,n1;n1 Yi=maxxij (8) yi=minxij (9) (2)记每个特征落在(yi,Yi)区间外的样本个数为ki。区间外的样本个数即为识别出的故障样本的个数,那么该特征的故障率为 (10) (3)SVDD、SVM以及SOM的识别率都按此方法依次计算。 表4显示了融合前后故障识别率对比结果。 表4 融合前后轴承状态识别率结果对比 由表4可以看出,融合前各特征对状态的识别率都不相同,并且相差很大,有些对故障的识别率很高,而有些对故障识别率则很低,因此,这就充分地表现出多特征在进行故障诊断时会顾此失彼,没有统一的状态评判标准。相反,经过融合后的识别率有很大的提高,在外圈故障的识别率上,SOM明显大于SVDD与SVM,而且SOM对正常状态与内圈故障的识别率更是达到了100%。 4.1 航空轴承失效监控试验系统 如图11所示,航空轴承失效监控试验系统主要由试验主体、动力及传动系统、润滑系统、液压加载系统、电气系统、计算机监控系统等组成。试验轴承安装在试验主体的轴系上,采用悬臂式结构;液压加载系统提供轴向和径向的可调加载力;传感器监测点分布如图12所示[12]。 图11 航空轴承失效监控试验系统实物图Fig.11 The physical map of test system of aviation bearing failure monitoring 图12 传感器监测点Fig.12 Sensor monitoring points 4.2 试验方案 由于轴承寿命普遍较长,正常试验极其耗费时间,因此采用轴承缺油条件加速轴承失效[12]。试验过程中振动信号的采集软件为南京航空航天大学智能诊断与专家系统研究室开发的航空轴承失效监控与寿命评估系统(BLES)实时采集振动信号。试验过程中各工况控制参数如下:转速12 000r/min、轴向载荷4kN、径向载荷3kN。试验步骤主要分为以下三个阶段: (1)润滑阶段。轴承在润滑状态下工作,保证试验前其具有良好润滑条件。 (2)干磨阶段。停止润滑,轴承进入加速退化阶段,直到试验进入系统保护。 (3)正式试验。重新开启润滑,轴承继续试验,直至终止试验。 下面选择一组滚动轴承试验数据,图13为轴承润滑阶段的振动有效值图,图14为轴承正式试验阶段的振动有效值图。 图13 润滑阶段振动有效值Fig.13 The RMS of lubrication phase 图14 正式试验阶段有效值Fig.14 The RMS of formal test phase 4.3 融合结果分析 在上文中已经通过试验验证了融合值对各类故障均敏感,但若想作为实际航空轴承状态监测的指标,融合值应满足一个条件:能反映轴承的劣化趋势。 利用本文方法对多维特征进行融合,得到润滑阶段和正式试验阶段下的融合值随时间变化的过程,分别如图15和图16所示。 图15 润滑阶段融合值Fig.15 The fusion value of lubrication phase 图16 正式试验阶段融合值Fig.16 The fusion value of formal trial phase 因此,由图15、图16可知,融合值在润滑阶段数据稳定,满足正常样本的数据波动情况;而在正式试验阶段,融合特征值随着轴承的状态变化而变化,能够反映轴承的劣化趋势。 为了判断轴承全过程数据的融合值是否仍然能够比有效值更能够区分出其正常、异常的状态,并能够提前区分出轴承的故障,采用数据分布的概率分布曲线进行滚动轴承的状态评估,结果如图17、图18所示。 图17 有效值数据概率分布曲线Fig.17 The probability distribution curve of RMS 图18 融合值数据概率分布曲线Fig.18 The probability distribution curve of fusion value 由图17、图18所示,融合值相比于有效值已经存在很明显的区分度。为了更加明显地表示两者的分离度,本文截取了横坐标0~40g阶段进行分析比较,结果如图19、图20。 图19 有效值数据概率分布曲线(截取)Fig.19 The probability distribution curve of RMS (intercept) 图20 融合值数据概率分布曲线(截取)Fig.20 The probability distribution curve of fusion value (interception) 由图19、图20对比可知,融合值的数据分布概率分布曲线相比于有效值的数据分布概率分布曲线,其润滑阶段与正式试验阶段的分离度更高。可知,在润滑阶段与正式试验阶段,融合数据相比于有效值特征数据更能提早地发现故障数据,因此,融合值对早期故障更加敏感,在故障的早期即能区分轴承的故障状态。 (1)自组织神经网络(SOM)能够实现多特征的自组织映射,本文利用自组织神经网络来实现特征融合,充分发挥了自组织神经网络在降低维数方面的突出优势,为准确评价滚动轴承运行状态提供了重要的方法。 (2)相比于单一特征量,融合特征量能够避免多特征在故障决策时的顾此失彼,成功对轴承状态进行故障诊断。 (3)相比于振动有效值,融合值对早期故障更加敏感,并且根据融合数据的分布情况能够很好地识别轴承的状态。 [1] 陈果, 李爱. 航空器检测与诊断技术导论[M]. 北京: 航空工业出版社, 2012:1-6.CHENGuo,LIAi.IntroductiontoAircraftDetectionandDiagnosisTechnology[M].Beijing:AviationIndustryPress, 2012:1-6. [2] 罗慧, 王友仁, 崔江,等. 电力电子电路多源特征层融合故障诊断方法[J]. 电机与控制学报, 2010, 14(4):92-96.LUOHui,WANGYouren,CUIJiang,etal.IntelligentFaultDiagnosisforPowerElectronicCircuitsBasedonMulti-sourceFeature-levelFusion[J].ElectricMachinesandControl,2010,14(4):92-96. [3] 古莹奎, 杨子茜, 朱繁泷. 基于主成分分析的齿轮箱故障特征融合分析[J]. 中国机械工程, 2015, 26(11):1532-1537.GUYingkui,YANGZiqian,ZHUFanlong.GearboxFaultFeatureFusionBasedonPrincipalComponentAnalysis[J].ChinaMechanicalEngineering, 2015, 26(11):1532-1537. [4] 李凌均, 张周锁, 何正嘉. 基于支持向量数据描述的机械故障诊断研究[J]. 西安交通大学学报, 2003, 37(9):910-913.LILingjun,ZHANGZhousuo,HEZhengjia.ResearchofMechanicalSystemFaultDiagnosisBasedonSupportVectorDataDescription[J].JournalofXi’anJiaotongUniversity, 2003, 37(9):910-913. [5] 蒋全胜, 贾民平, 胡建中,等. 基于拉普拉斯特征映射的故障模式识别方法[J]. 系统仿真学报, 2008,20(20):5710-5713.JIANGQuansheng,JIAMingping,HUJianzhong,etal.MethodofFaultPatternRecognitionBasedonLaplacianEigenmaps[J].JournalofSystemSimulation, 2008,20(20):5710-5713. [6] 张伟, 周维佳, 刘晓源. 基于扩展LLE方法的非线性系统故障诊断研究[J]. 电子学报, 2015, 43(9):1810-1815.ZHANGWei,ZHOUWeijia,LIUXiaoyuan.AnImprovedLLE-basedApproachtoFaultDiagnosisofNonlinearSystem[J].ActaElectronicaSinica, 2015, 43(9):1810-1815. [7] 刘志川, 唐力伟, 曹立军,等. 基于Isomap和IGA-SVM的齿轮箱故障诊断研究[J]. 机械强度,2016,38(1):38-43.LIUZhichuan,TANGLiwei,CAOLijun.ResearchonGearboxFaultDiagnosisBasedonISOMAPandIGA-SVM[J].JournalofMechanicalStrength, 2016,38(1):38-43. [8] 袁宪锋, 宋沐民, 周风余,等. 多PCA模型及SVM-DS融合决策的服务机器人故障诊断[J]. 振动、测试与诊断, 2015(3):434-440.YUANXianfeng,SONGMumin,ZHOUFengyu.ExperimentalandAnalyticalStudyofDynamicResponseofStructureControlledbyActive-passiveHybridTuneMassDamper[J].JournalofVibrationMeasurement&Diagnosis, 2015(3):434-440. [9]ZHANGQ,HUAC,XUG.AMixtureWeibullProportionalHazardModelforMechanicalSystemFailurePredictionUtilisingLifetimeandMonitoringData[J].MechanicalSystems&SignalProcessing, 2014, 43(1/2):103-112. [10]YUJ.BearingPerformanceDegradationAssessmentUsingLocalityPreservingProjectionsandGaussianMixtureModels[J].MechanicalSystemsandSignalProcessing, 2011, 25(7): 2573-2588. [11]PANY,CHENJ,LIX.BearingPerformanceDegradationAssessmentBasedonLiftingWaveletPacketDecompositionandFuzzyC-means[J].MechanicalSystemsandSignalProcessing, 2010, 24(2): 559-566. [12] 汪瑾, 陈果, 王洪伟,等. 基于后验概率SVM的航空发动机滚动轴承状态评估[J]. 轴承, 2015(5):55-59.WANGJin,CHENGuo,WANGHongwei,etal.ConditionAssessmentforAero-engineRollingBearingBasedonPosteriorProbabilitySVM[J].Bearing, 2015(5):55-59. [13]CHAUDHARYV,BHATIARS,AHLAWATAK.ANovelSelf-organizingMap(SOM)LearningAlgorithmwithNearestandFarthestNeurons[J].AlexandriaEngineeringJournal, 2014, 53(4):827-831. [14]KURDTHONGMEEW.ALowLatencyMinimumDistanceSearchingUnitoftheSOMBasedHardwareQuantizer[J].Microprocessors&Microsystems, 2015, 39(2): 135-143. [15] 高隽. 人工神经网络原理及仿真实例[M]. 北京: 机械工业出版社, 2007:168-173.GAOJuan.ArtificialNeuralNetworkPrincipleandSimulation[M].Beijing:MechanicalIndustryPress, 2007:168-173. [16] 杨淑莹. 模式识别与智能计算[M]. 北京: 电子工业出版社, 2011:170-176.YANGShuying.PatternRecognitionandIntelligentComputing[M].Beijing:PublishingHouseofElectronicsIndustry, 2011:170-176. [17]CHENG,HAOTF,WANGHF,etal.SensitivityAnalysisandExperimentalResearchonBallBearingEarlyFaultDiagnosisBasedonTestingSignalfromCasing[J].JournalofDynamicSystemsMeasurement&Control, 2014, 136(6):061009. (编辑 王艳丽) Condition Assessment for Rolling Bearings Based on SOM ZHANG Quande1CHEN Guo1LIN Tong1OUYANG Wenli2TENG Chunyu2WANG Hongwei3 1.College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016 2. Basic Research Office, Avic China Aero-polytechnology Establishment, Beijing, 100028 3. The Sixth Research Office, Beijing Aeronautical Technology Research Center, Beijing, 100076 Aiming at the problems that single feature fault diagnosis accuracy was not too high, a rolling bearing condition assessment method was proposed based on SOM herein. Firstly, the multi-dimensional features were extracted from the original vibration signals and preprocessed by PCA, a fusion model was established by training SOM network and weight vectors of competitive neuron were obtained. Secondly, the fusion index, which was the minimum Euclidean distance between every sample values to the competitive neuron weighting vector, was achieved. Finally, the conditions of rolling bearings were classified by comparing the minimum Euclidean distances among the detected samples and the normal samples. The proposed method herein was applied to condition assessment of the rolling bearings, and the test results show that the fusion index is more sensitive and robust than that of original single feature during the stages of early faults; meanwhile, the fusion index may reflect the states of rolling bearings more accurately. self-organization mapping(SOM); principal component analysis(PCA); feature fusion; minimum matching distance; rolling bearing; fault identification 2016-04-15 国家自然科学基金资助项目 (51675263) V263.6 10.3969/j.issn.1004-132X.2017.05.008 张全德,男,1991年生。南京航空航天大学民航学院硕士研究生。主要研究方向为航空器监测、诊断与健康管理。陈 果(通信作者),男,1972年生。南京航空航天大学民航学院教授、博士研究生导师。E-mail:cgzyx@263.net。林 桐,男,1993年生。南京航空航天大学民航学院硕士研究生。欧阳文理,男,1988年生。中航工业综合技术研究所基础研究室工程师。滕春禹,男,1977年生。中航工业综合技术研究所基础研究室工程师。王洪伟,男,1979年生。北京航空工程技术研究中心第六研究室高级工程师。
4 滚动轴承性能退化试验








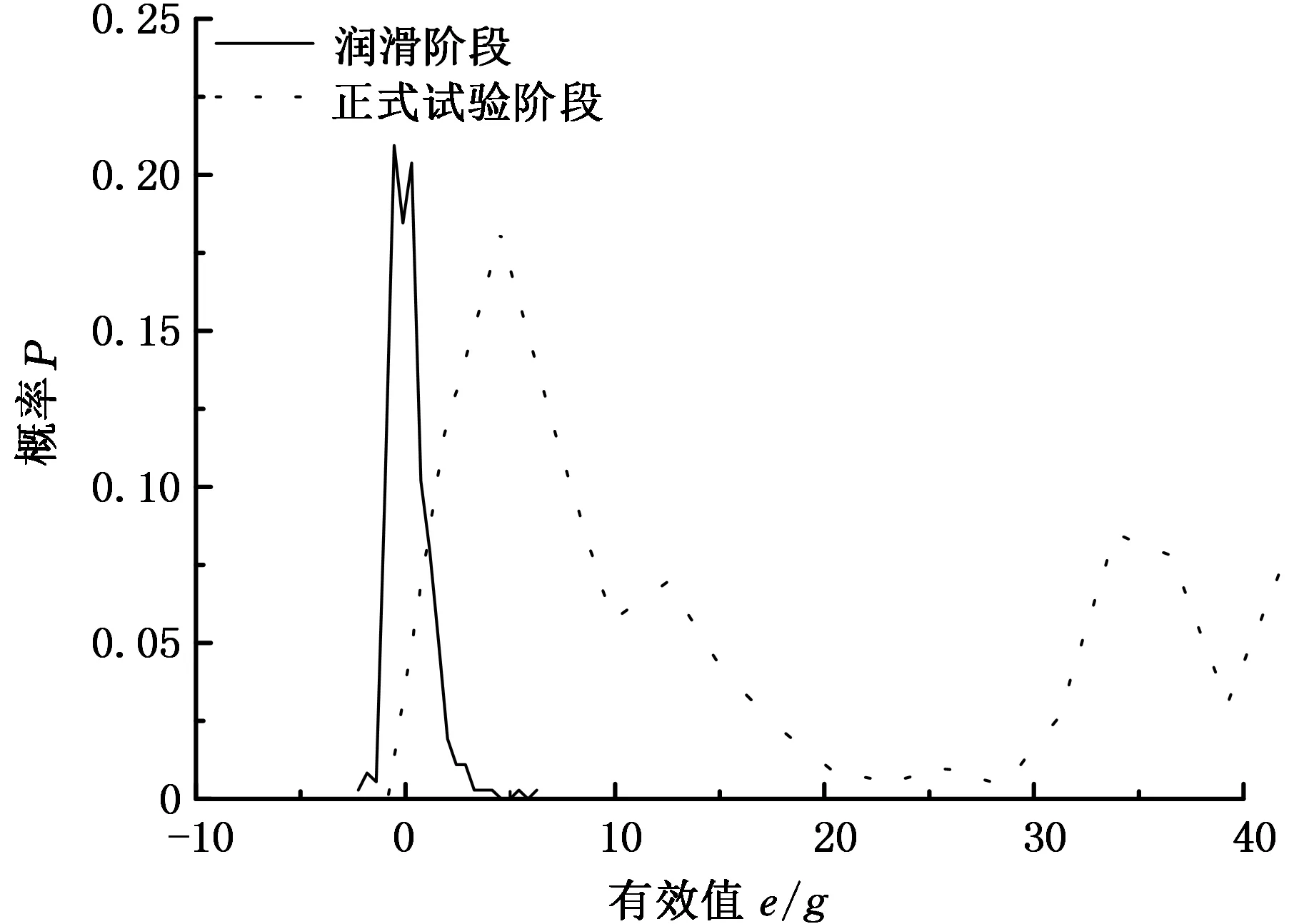
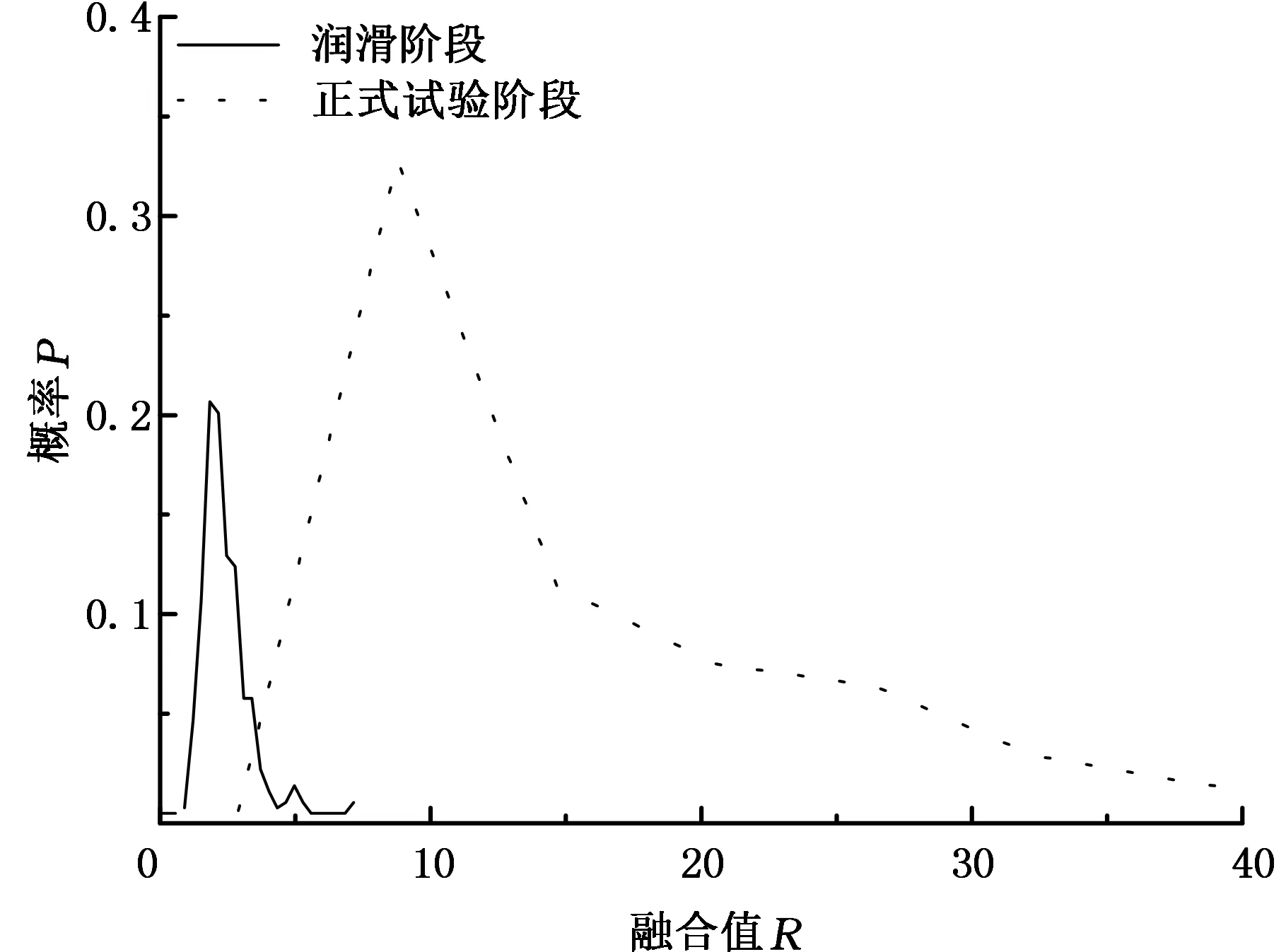
5 结论
