基于傅立叶变换的乐音分析和生成
2017-03-13大连经济技术开发区第一中学徐琦喆
大连经济技术开发区第一中学 徐琦喆
基于傅立叶变换的乐音分析和生成
大连经济技术开发区第一中学 徐琦喆
人类听觉能听到乐音、噪音等声音,乐音是一种较和谐的声音。乐音作为一种周期性信号,时时刻刻地存在于人们的生活当中。并且随着计算机的广泛深入应用,通过研究这种信号我们可以合成我们需要的电子音乐等等。在本文中主要分析通过傅立叶方法来研究乐音。对原信号使用离散傅立叶变换研究乐音的组成原理,并运用离散傅立叶逆变换进行音乐的生成。基于傅立叶方法,我们不仅分析音乐的组成,也提出一种利用计算机生成乐音的思路。
信号分析;信号生成;离散傅立叶变换
一、引言
人类听觉可以听到的声音包括乐音、噪音等等,而乐音是一种相对噪声来说比较和谐的声音。而乐音是有乐器的周期性震动发出声波形成的,而声波就可以用信号来描述。
所谓信号,就是随时间变化的函数。而乐音明显是一种周期性信号,所以我们用傅里叶变换的方法去研究乐音的规律,并遵循这种规律去合成我们想要的电子音乐。
在接下来的文章中会对乐音产生的基本原理、分析信号的实验方法、得到的实验结果进行分析。
二、基本原理
人类听觉感受到的声音大体上可以划分为噪音、语音、乐音……几种类型。在乐音中用通讯与电子技术的术语解释就是周期信号频率随时间节奏变化的一种表述。乐谱上的每个音符表达了此时此刻规定出现的信号频率和持续时间。
在乐谱中我们用大写英文字母C D E F G A B表示每个音的音名,当指定某一音乐时,它对应固定的基波信号频率。在图中表示出钢琴键盘结构,我们可以通过计算机得到每个琴键对应的基波频率值。
乐音的基波对应为每一个音名,而乐音谐波则影响着音色。各种乐器发出fA1 = 440Hz的乐音,在人听觉中会有明显差异,这是由于谐波成分有别,频谱结构各异。在电子乐器制造时,应该尽力模仿实际乐器的谐波结构,以达到逼真的音乐效果。
最后我们要对音调的持续时间进行分析每个音调都可以用连续的一段正弦信号并带有一小段静音(停顿)来表示。每个音调的持续时间取决于它是全音符、二分音符……而每个音符之后的停顿时间应该是相同的,不随音符的长度而变化。
接下来,我们会用傅立叶变换和傅立叶级数分析和生成音乐,傅里叶方法把时域的信号在频域展现出来,也就是说在我们直观观察信号的时域转换到表征每个频率分量强度的频域上来。通过这样的转换,不仅信息没有丢失,还把我们更需要的特征展现出来。
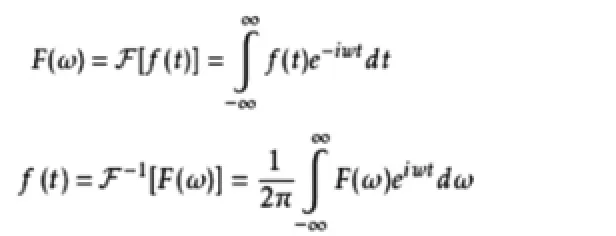
基本思路是我们需要先将原信号傅里叶变换保留重要频谱,即基波分量和各次谐波分量,滤除掉其他,这也是我们构造电子音乐的基本思路。

而我们的乐音信号在理想情况下也是周期信号,所以也可以通过傅立叶级数可以转化为正弦函数和余弦函数叠加的形式。
三、实验方法
在研究分析傅立叶变换与语音的关系前我们应首先了解并掌握简单的音乐合成。我们根据某段音乐的简谱和“十二平均律”计算出该片段中各个乐章的频率,并在MATLAB中生成幅度为抽样频率为8kHz的正弦信号表示这些乐音。用sound函数播放每个乐音,最后用这一系列乐音信号拼出音乐片段,感受合成后的音乐。
接着我们应先通过傅立叶变换分析音乐。我们用原始音乐和我们基于信号处理方法生成的音乐作比较,它们的抽样率都是8kHz。下面,我们用wavread函数载入第一段信号的文件,并听取播放出的音乐,感受播放出的效果怎么样。除此之外,我们接着研究一下这段音乐的基频是多少,是哪一个音调。并且用傅立叶级数或变换的方法分析它的谐波分量是多少。
最后,在我们了解了如何简单的合成音乐和用傅立叶变换分析乐音后,我们要运用傅立叶级数合成音乐。我们能生成出用某种乐器弹奏某段音乐的信号。我们运用之前计算出的傅立叶级数试着在乐音信号中加入一些谐波分量,我们可以感受一下音乐是否更有厚重感,是否像那个乐器真实演奏出的声音。
四、实验结果
我们选取某个音乐的片段,在合成并听完音乐后,我们发现,如果仅用MATLAB形成乐音信号并将信号拼接得到的音乐是可以准确辨别音高的,并且每两个音之间没有间断,听不出拍的感觉。正因为是这样得到的声音显然不是自然发出的,而是“人工制造”的。
当我们用wavread函数载入乐音信号后从整体的波形来看,音符的混叠更加充分,每个音之间的界限并没有那么清晰;它的包络更加写实,长短不一的指数衰减;当我们看到局部放大的波形,声音中混有非线性谐波和噪音,真实的声音都会具有这些,但是刚才仅通过MATLAB等合成并拼接得到的合成音乐没有这些分量,是十分规整的波形,因此合成的音乐与真实的音乐相差较大。
分析谐波分量时,简单的方法是近似地取出一个周期求傅立叶级数,但是这样求得的答案显然是不准确的,因为已经发现基音周期不是整数。而用复杂的方法是对整个信号求傅立叶变换,但是会发现无论如何提高频域的分辨率,也得不到精确的包络。在其中用的方法是增加时域的数据量,也就是从少到多的观察周期,依次来分析它的谐波量。
下面如图,延扩不同周期,基频不变,各级傅立叶级数比例不变,但频谱更加突出。不过这得益于波形几乎为整数周期。
我们通过计算的傅立叶级数再次完成对该乐曲的合成和加工,但是得到的音乐并不是很像,其中是由于吉他的泛音并不完全相同。

如果想要将音乐相似度更大一点,可以将泛音提取更多,更准确;并且在其中引入类似噪声之类的东西以增加真实性;另外吉他有共鸣箱,我们可以引入类似的模型。
五、结论
傅里叶方法是研究乐音组成原理的有效方法,也是利用计算机构造电子合成乐音的有效工具。其中,由于计算机中存储的都是离散化之后的信号,所以此处我们使用离散傅里叶变换。
在研究乐音组成原理,我们对原信号使用傅里叶变换方法,并提取针对基波和谐波对应的频谱,发现各个频谱的总体幅度决定其音量,而各个频谱幅值的相对比例由发出声音的乐器种类决定。
在生成音乐过程中,我们需要用的离散傅里叶逆变换,也就是由给定的音符和持续时长自动生成乐音信号波形,并且通过这种方法能生成的电子音乐和真实乐音符合度很高。
综上,我们基于离散傅里叶变化和离散傅里叶逆变换,不仅对乐音组成原理进行了详细的阐述,也提出了一种利用计算机生成乐音的思路。
[1]易昆南,李慧,赵澍源,等.让枯燥无味的数学变得“有趣、有味、有惑”——Matlab中的音乐合成[J].实验室研究与探索,2014,33(6): 114-117.
[2]杨若芳,项顶.基于Matlab实现音乐识别与自动配置和声的功能[J].自动化与仪器仪表,2011(1):126-128.
[3]程美芳.钢琴音色识别与电子合成系统的设计与实现[D].电子科技大学,2014.
