光伏模块并网的新型非线性控制方法

,,,,,,,

(国网浙江平湖市供电公司,浙江 嘉兴 314200 )

1 引言

随着经济和社会的发展，能源消耗越来越大，环境污染和电力需求的迅速增长使得人们越来越重视可再生能源的发展。光伏能源具有免费、丰富、无污染和分布最广泛的特点而被考虑为最为关注的能源之一。它既可在偏远地区实现孤岛运行，也可以在市区实行并网运行。在过去的一些年里，随着技术的发展使得光伏电池板的转换效率已经取得了很大的提升，另一方面，随着光伏产业的飞速发展，使得光伏系统更加的有效和可靠，尤其在分布式电源的中低压能源系统中更为明显。将分布式电源并入电网可以部分缓解对电能需求上升的压力。

光伏并网代表了太阳能最重要的应用领域。并网逆变器是光伏并网发电系统的核心部件，它的主要功能是将光伏阵列转化的直流电变换成与电网同步的交流电，其控制的好坏直接关系到系统的整体性能，因此得到了很多研究工作者的关注。

由于传统的双环控制策略具有控制简单，较好的稳定性和动态性能，因此得到了广泛的应用，是目前最主要的控制方法。但传统方法在功率突变时存在响应滞后，稳定性较差的缺点，针对传统控制策略的缺陷，研究学者也提出了一些新的控制算法包括人工神经网络[1-2]、自适应[3]、滑模变结构[4]、模糊控制[5-6],它们在各自领域解决了某些控制问题,但也表现出了各种相应的局限性。人工神经网络控制的精度依赖于模型训练样本；自适应控制要求在线辨识对象模型,算法复杂、计算量大；滑模变结构控制存在系统抖振问题；模糊控制依赖于隶属函数的选取,控制精度有待提高等缺陷。

在早期也使用过非线性控制方法包括瞬时比较方式[7]和三角波比较方式[8]。瞬时比较方式具有实现简单,良好的动态响应和内在的电流保护功能，但存在输出电流波动、谐波畸变率都很大的缺点。三角波比较方式虽然输出电压中所含谐波较少(含有与三角波相同频率的谐波),器件的开关频率固定(等于三角波的频率);但该方法硬件较为复杂,跟随误差较大,电流响慢的特点。本文基于系统光伏电池，变压器和逆变器的非线性特性而提出了一种新的非线性控制方法：后推法。

本文提出的后推法可以克服上述缺点，且在功率骤变时，大幅度的提高系统的稳定性和响应速度(如：当输入功率发生变时，采用新的控制方法，实现并网电流的稳定所需的时间将少于0.1s)，并具有硬件简单，算法简洁，易于实现的特点，最后，通过仿真平台和实验结果证明了所提控制策略的可行性。

2 单相光伏发电系统的模型

一个典型的单相光伏系统并网模型如图1所示：它包涵有一个光伏阵列，一个输入电容ci，一个用来提高光伏板的电压和追踪光伏阵列的最大功率点的升压斩波电路，一个直流母线电容器cdc，一个单相全控型的逆变器(将直流转换为交流，同时实现单位功率因素的并网)，一个滤波电感。

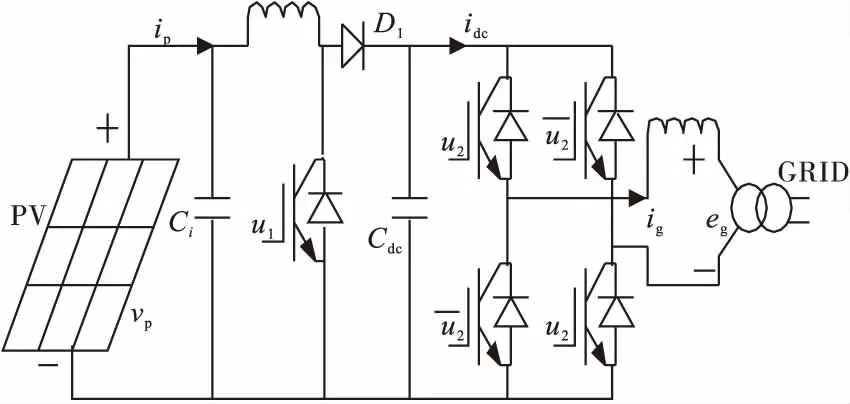
图1 光伏系统并上单相电网模型

光伏组件阵列作为能源转换器件，它的输出功率不仅受环境温度和光照强度这些外界因素的影响外，还受到其端电压vp的影响。由其功率—端电压曲线可知，控制vp就可以决定光伏的输出功率。MPPT 控制的意义就是搜索到vp的参考值，保证光伏组件阵列在任何时刻输出最大功率，提高光电转换效率。

3 系统的整体模型

通过PWM信号来控制斩波器的μ1和逆变器的μ2，其值设置为(0 ，1)。根据基尔霍夫定律，对图1中的斩波器和逆变器输入连续的0,1信号。可以得到一个平均模型如下：

(1a)

(1b)

(1c)

(1d)

式中,Ri是输入电感Li的串联等效电阻；x1代表光伏板输出电压vp;x2代表电感电流iLi；x3代表直流母线电压vdc；x4代表待并网电流iLg；ip代表光伏板输出电流ip；μ1代表斩波器二进制控制输入μ1；μ2代表逆变器二进制控制输入μ2，μ1和μ2在0,1之间连续变化，通常称之为占空比,作为输入控制信号。

4 控制器设计

在这部分,介绍了一种控制器。它可以实现闭环系统的全局稳定,能精确地实现最大功率点的追踪，实现单位功率因素的并网，严格控制直流母线电压。

4.1 实现最大功率点的追踪

在这里采用后推法设计原则来进行最大功率点的追踪，追踪误差可以表示为：

z1=x1-vm

(2)

为了达到追踪的目的是使的z1等于零。式(2)和(1a)可以进一步推出：

(3)

式中,x2/ci的数值代表了一个虚拟的控制变量。考虑二次李雅普诺夫函数：

(4)

将v1对时间进行积分并结合(4)可得

(5)

从上式可以看出当x2/ci=M时追踪误差可以达到零。其中M定义如下：

(6)

其中c1是一个设计参数。因为x2/ci不是实际的控制输入，所以只能尽量寻求x2/ci-M收敛到零。为此定义了第二个误差变量：

z2=x2/ci-M

(7)

接下来通过确定控制信号μ1的变化规律来逐渐消除z1和z2的误差。通过式(7)等式(3)可以变为：

(8)

同样，李雅普诺夫函数的微分(6)可以化为：

(9)

通过(7)、(1b)、(8)式可以推出下式 ：

(10)

最终的目的是确定控制信号μ1使整个系统稳定基于状态向量(Z1,Z2)。

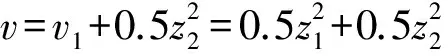
(11)

将v对时间进行积分可得：

(12)

其中c2>0是一个设计参数。从等式(12)可知当

(13)

时(z1,z2)=(0,0)实现了全局的渐进稳定。联立(10)和(13)可以得到μ2的控制规律

(14)

4.2 最大功率点对应电压的确定

最大功率点MPPT(Vm,Pm)可以通过下式获得:

(15)

此时vp=Vm，既最大功率点对应的电压。通过调节占空比μ1，不管温度辐射如何变化，都要保证∂p/∂vp等于零。这个理想的电压可以通过变步长电导法得到。其核心是：在光伏电池的输出功率接近最大功率点时，使用较小的步长，在远离最大功率点时，使用较大的步长变步长电导增量算法的原理表达式如下：

(16)

其Δvm(k)和vm(k-1)分别为第k和k-1次MPPT算法输出的光伏电池参考电压，N为适应采样周期调节步长的缩放系数。变步长电导法其性能主要由参数N所决定。参数N的调节可以通过如下原则进行：

(17)

其中，ΔVmax是定步长电导增量法的最大步长，若满足上述不等式(17)条件时，为变步长算法，且步长按式(16)中的步长选取，若不满足上述不等式(17)时，则为定步长，且步长为ΔVmax。流程图如图2所示。

4.3 控制逆变器实现单位功率因素并网及严格控制母线电压

(1)实现单位功率因素并网

(18)

其中β是时变性的正实数。该调整器采用了后推技术，电流误差可以表示如下

(19)

结合等式(1d)，将上式对时间求导可得：

(20)

为了从这个一阶等式中找到稳定的控制规律，考虑二次李雅普诺夫函数

(21)

如果控制信号μ2满足下列条件(22)，很容易验证v3对时间的导数是关于z3的一个负定函数。

(22)

其中c3>0是一个设计参数。如果按上述配置，则有：

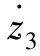
(23)

(24)

这意味着这个平衡(z3=0)是全局稳定，因此单位功率因素并网可以达到。

(2)直流母线电压调节

目标在于为(18)式中的比例β设计一个 变化规律，使逆变器的输入电压x3=〈vdc〉 尽可能的接近被给的恒定的参考电压Vd>0。使用下面的PI-1控制法可以实现这一目标。

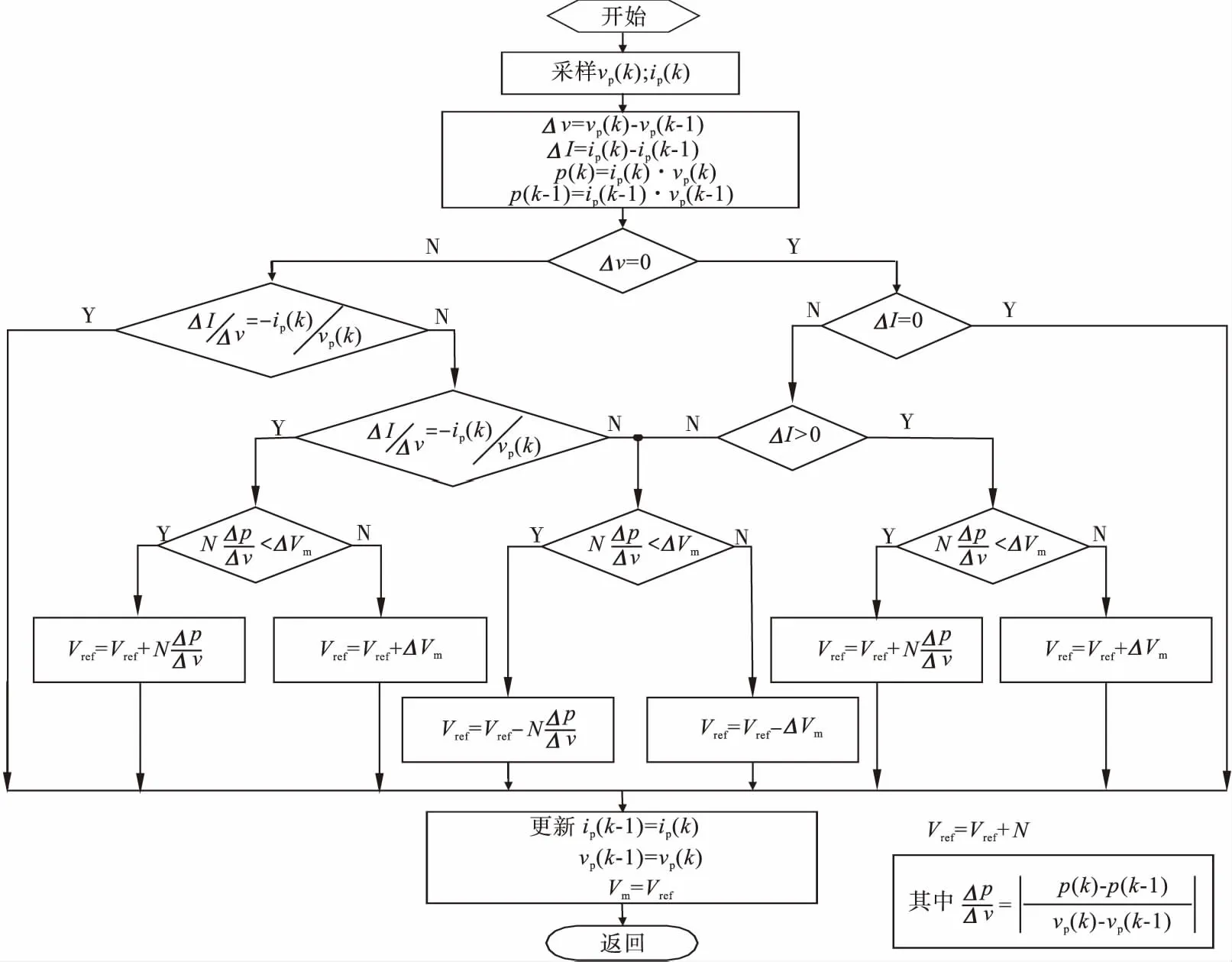
图2 最优电压生成

β=G1(s)εdc

(25a)

(25b)

εdc=x3-Vd

(25c)

通过上述调节可以实现追踪误差到零,从而使直流母线电压的严格监管。

5 仿真结果

为了验证上述理论的有效性，实验设置如图3，通过matlab对其进行仿真，测试主要参数见表1。该控制系统采用了瞬时模型对其经行模拟，而控制器的设计采用的是平均模型(2a-d)。闭环控制系统的仿真结果见图4～图7。

5.1 辐射变化效应

图4显示了光子辐射变化时追踪最大功率点(P,V)的特性 。通过查找仿真所用光伏阵列的PV特性曲线可以查到，当温度不变时(25℃),辐射强度从400～1000W/m2，辐射对应曲线的最大功率点分别为70.8～183.1W。从图4的仿真结果可以看到其功率输出分别对应于最大功率点(70.8 ， 183.1)。这个数据显示了当输出功率剧变时调节直流母线电压vdc，只需经历很短的时间就可达到预期的目标值Vd=48V。图5显示了并网电流iLg和并网电压eg。从图中可以清晰地看到并网电流iLg是正弦波且与电压eg是同相位，因此实现单位功率因素并网可以实现，同时也可以看到当电池输出功率发生剧变是并网电流的稳定所需的时间少于0.1s。

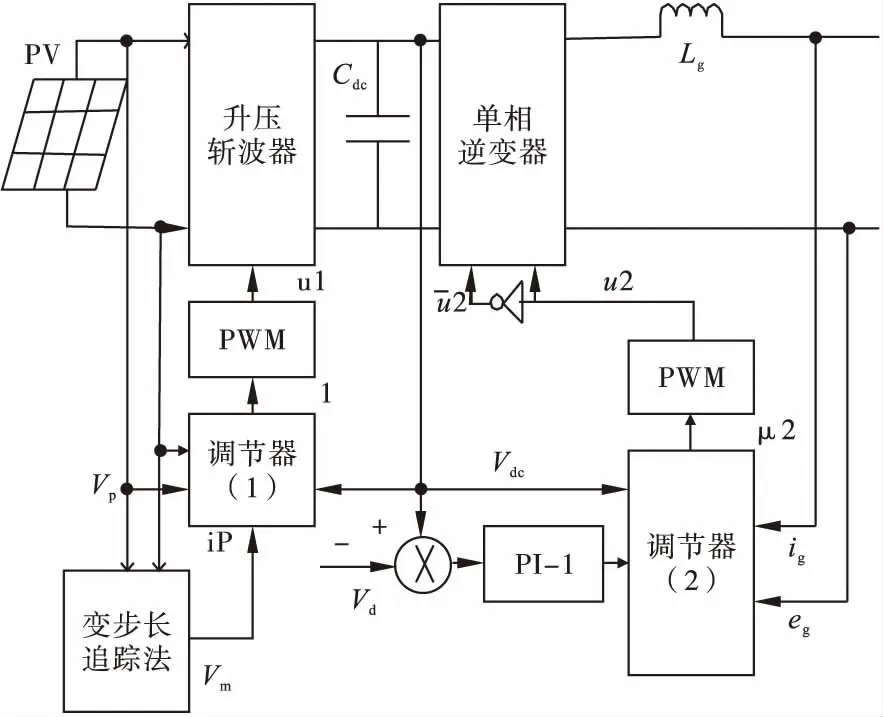
图3 单相并网连接控制系统图

5.2 温度变化效应

图6显示当温度变化时控制器的特性。当光子的辐射强度λ不变(1000W/m2)。温度变化从25°C到60℃时，可以看到控制器使整个系统工作在一个最佳状态。可以看到通过追踪最大功率点达到的183.1W和153.4W分别对应于模拟光伏阵列，温度在60℃和25℃时对应的最大功率点。这个数据也显示了当输出功率剧变时调节直流母线电压vdc，只需经历很短的时间就可达到预期的目标值Vd=48V 。图7显示了并网电流iLg和并网电压eg。从图中也可以清晰地看到并网电流iLg是正弦波且与电压eg是同相位，因此实现单位功率因素并网可以实现。同理也可以看到当电池输出功率发生剧变是并网电流的稳定所需的时间少于0.1s。

表1 仿真测试主要参数

图4 辐射变化时MPPT和直流母线的特性

图5 辐射变化时单位功率因数并网

图6 温度变化时MPPT和直流母线的特性

图7 温度变化时单位功率因数并网

6 总结

本文基于系统光伏电池，变压器和逆变器的非线性特性而提出了一种新的非线性方法(后推法)来控制光伏系统的并网，这种控制策略更适合系统的非线性特性。通过理论分析和仿真证实了其可以实现最大功率点的追踪；维持直流母线电压的恒定；实现单位功率因数的并网；实现整个闭环系统的稳定，并可以在功率骤变时，克服传统的双环控制响应滞后，系统稳定性较差的缺点，大幅度的提高系统的稳定性和响应速度。

[1] KYOUNGSOO R,RAHMAN S.Two-loop controller for maximizing performance of a grid-connected photovoltaic-fuel cell hybrid power plant[J].IEEE Trans on Energy Conversion,1998,13(3):276-281.

[2] TORRES A F.A three-phase grid-connected PV system[M].Proceedings of 26th Annual Conference of the IEEE Industrial Electronics Society:Vol 1，Oct 22-28,2000,Nagoya,Japan.Los Alamitos,CA,USA;IEEE Computer Society，2000;723-728.

[3] MARTINS D C,DEMONTI R.Grid connected PV system using two energy processing stages[M].Record of the 29th IEEE Photovoltaic Specialists Conference,May 19-24,2002,New Orleans,LA,USA.Piscataway,NJ，USA:IEEE,2002:1649-1652.

[4] MEZA C,BIEL D,MARTINEZ J,et al.Boost-buck inverter variable structure control for grid-connected photovoltaic systems[M].Proceedings of IEEE International Symposium on Circuits and Systems,May 23-16，2005，Kobe,Japan.Piscataway,NJ，USA;IEEE,2005:1318-1321.

[5] PREMRUDEEPREECHACHARNS,POAPORNSAWAN T.Fuzzy logic control of predictive current control for grid-connected single phase inverter[M].Record of the 28th IEEE Photovoltaic Specialists Conference,Sep15-22,2000,Anchorage,AK,USA.Piscataway,NJ,USA;IEEE,2000;1715-1718.

[6] DAMS A J,SALAMEH Z M.Fuzzy logic modeling of a grid-connected mind/photovoltaic system with battery storage[M].Proceedings of Large Engineering System s Conference on Power Engineering,Jul 28-30,2004:NovScotian,Canada.Piscataway,NJ,USA:IEEE,2004:129-135.

[7] 赵争鸣，刘建政，孙晓瑛，等.太阳能光伏发电及其应用[M].北京:科学出版社，2005.

[8] 王兆安，杨君，刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社，2004.

[9] 董密,罗安.光伏并网发电系统中逆变器的设计与控制方法[J].电力系统自化，2006，30(20)97-101.

[10] 马皓,林钊,张宁,等.逆变器并联系统开关环流的建模和分析[J].中国电机工程学报，2015，22(11)：50-54.

[11] 王飞，谢磊，周毅人，等.单相光伏并网逆变器的控制策略研究及实现[J].电力电子技术，2009，43(11)：24-25.

[12] 范瑞祥,刘斌,周银星.基于自适应重复控制的并网电流控制研究[J].电力电子技术,，2015，12(33)：103-107.

[13] Zmood D N，Holmes D G，Bode G H.Frequency-domain analysis of three-phase linear current regulators[J].IEEE Trans.on Industrial Electronics，2013，37(2)：601-610.

[14] 刘文业,罗隆福,张志文,等.基于时基的恒频自适应电流控制技术 [J].电力系统自动化，201401(9)：19-20.

[15] 李小叶,李永丽,张玮亚,等.基于多功能并网逆变器的电能质量控制策略[J].电网技术，2015，2(31)：35-42.