基于改进粒子群算法的负荷不平衡调整策略
2017-03-13,,,
,,,
(1.福州大学电气工程与自动化学院,福建 福州 350108;2.国网福建电力有限公司南平市供电公司,福建 南平 353000)
1 引言
在配电网中,尤其是农村电网,三相负荷不平衡问题较为突出。三相负荷不平衡会使得变压器及线路损耗增加,变压器和线路的容量无法得到充分的利用以及输电效率降低。
引起三相负荷不平衡的原因主要有:三相所带负荷的大小、性质不完全相同;线路上存在谐波源。对于前者导致的不平衡问题,可以通过换相调整负荷的接入相别使得三相的总负荷在大小、功率因数上接近相同;对于后者,往往是通过安装电力滤波器(有源滤波器、无源滤波器)以滤除高次谐波。本文主要研究由于三相所带负荷不同而引起的不平衡问题,采用调整负荷相别的方法改善三相负荷不平衡。
就换相调整的方法而言,可以分为人工换相和自动换相两种。人工换相根据用电信息结合理论和经验确定出应该改变相别的负荷,然后在停电的情况下手动进行换相操作。而自动换相指利用换相开关和换相策略调整负荷相别,其硬件包含换相开关、主站及通信模块三个部分。如图1所示,换相开关安装在三相转单相的节点处,其输入端为三相四线电源,输出端为单相负载的火线和零线。从原理上,换相开关可看成是一个单刀三掷开关,改变开关的投掷位置也就改变了单相负荷的接入相别。换相开关实时发送电压、电流、功率因数、当前接入相别等数据给主站,主站通过换相算法下发控制命令。主站与换相开关之间采用GPRS/3G的通信方式。自动换相充分利用了现代信息技术、通信技术、单片机技术实现检测、分析和控制一体化,与人工换相相比,具有跟踪负荷在线调整的优点,可以显著降低运行人员的劳动力强度,提高台区的运行效率。

图1 换相开关工作原理图
国内有不少专家学者研究人工换相、利用换相开关或智能配电箱等调整三相平衡的方法。文献[1]提出了就地平衡补偿方法,通过调整用户的接入相别使得用电户、区段、线路出口、配变低压出口尽可能地接近于平衡,但该方法实施前需要调查用户的用户情况。文献[2,3]提出了采用遗传算法搜索换相的调整方法。其目标函数是使得中性线电流或三相电流的不平衡度尽可能地接近于零以及换相动作次数最少。文献[3]研究的对象是小区单元楼的三相平衡,这类平衡与农村配电台区的平衡有所不同。实际中小区单元楼一般在每一栋单元楼实现三相平衡,以尽可能地减少不平衡电流在线路上引起的附加损耗。而农村配电台区则没有这种条件调节三相平衡。文献[4]采用粒子群算法求解负荷换相调整问题,但用户的个数等于搜索空间的维数,随着用户个数的增加,容易造成“维数灾”,不利于快速搜索。
本文利用了粒子群算法优化换相开关的相别选择,采用了三进制编码法将换相优化问题转换成一元函数最值问题,降低了维数,提高了搜索效率。同时针对负荷换相问题的实质,对基本粒子群做了一些改进以适应问题的求解。与枚举法相比较,所提出的粒子群算法在保证较高准确度的同时具有较快的求解速度。
2 负荷换相的目标函数
三相负荷平衡的最终目标是使得三相负荷在大小及性质上尽可能的相等。当三相负荷平衡时三相线路所接的导纳相等,流过的电流大小相等,相位上互差120°,且流过中性线上的电流为零。
当三相负荷是不平衡时,则上述结论显然不成立。此时中性线上的电流可能由于零序分量的存在而不为0,三相电流的大小、相位差也可能因为负序和零序分量的存在而受到影响。
考虑到实际中获取电流的相位数据比较困难且在负载性质差不多的情况下,三相电流大小越接近,一般地相位差也接近于120°,因此忽略电流的相位关系而只考虑电流的大小关系,由此可得到不平衡负荷调整的目标函数。
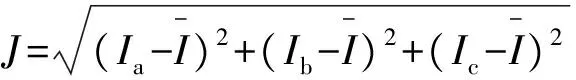
(1)
Iph=Iph1+Iph2+…+Iphm+Iph(m+1)+…Iphn
(ph=a,b,c)
(2)
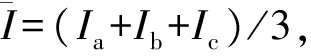
3 改进的粒子群算法求解方法
粒子群算法最初是由社会心理学博士Kennedy和电子工程学博士Eberhart受鸟群聚集行为的启发而提出的一种优化算法。这种算法将非线性问题的求解比拟鸟群寻找栖息地的过程,搜索空间中的解空间相当于鸟群要寻找的栖息地。相对其他的群智能算法而言,粒子群算法中每个个体服从的规律极为简单,而且求解结果相对精确,因此应用在很多领域。
根据粒子群理论,鸟群中的每只鸟被简化成一个具有位置和速度两种属性的粒子,每个粒子的运动规律如式(3)所示。
vij(t+1)=ωvij(t)+c1rand(pbestij(t)-xij(t))+
c2rand(gbestj(t)-xij(t))
xij(t+1)=xij(t)+vij(t+1)
(3)
式中,vij(t),xij(t)分别是t时刻第i个粒子第j维的速度和位置;c1,c2是系数,通常都取为2;ω是惯性权重系数,随着迭代次数的增加,从0.9线性递减到0.4。rand是[0,1]的一个随机数。pbestij(t)是第i个粒子第j维的历史最优位置,表征该粒子自身的飞行经验,gbestj(t)是t时刻全部粒子第j维的历史最优位置,表征整个粒子群的社会经验。
由上式可知,每个粒子的运动速度和位置包含了3个部分。第一部分是自身的速度,第二部分是自身的认知能力,通常称为认知部分,第三部分体现的是整个粒子群间的信息共享,通常称为社会部分。在第二部分和第三部分都乘于一个[0,1]的随机数,是考虑让认知部分和社会部分的影响力变得不确定,从而使得优化过程影响因素不至于绝对化,提高算法的灵活性。
换相开关的换相优化问题不能直接应用基本的粒子群算法求解,因为该问题本质上是整数规划问题,每个换相开关的开关位置只有3种情况(即换相开关的开关位置在A相、B相、C相),而基本的粒子群算法处理的是非线性优化问题。若直接对基本的粒子群算法的结果取整,虽然可以求解,但由于求解的问题维数太多,求解的速度会变得很慢。
考虑到每个换相开关只能在三相之间调整,因此采用三进制的编码方法,即把每一维当成一位,则多维问题就可以转换成一维问题。例如,用0012表示某种情况下4个换相开关的开关位置,其中,换相开关1和2处于A相,换相开关3处于B相,换相开关4处于C相,如图2所示。

图2 编码方法
采用上述的编码方法后,由于每个换相开关的权重是不一样的,需要对换相开关所在的支路进行排序。排序的依据是支路电流的大小。支路电流越大,则权重也越大,相应的位置比较靠前;反之,权重较小,位置比较靠后。通过排序运算,可使得负荷较轻的支路优先考虑换相,负荷较重的支路在轻载支路的调整效果不明显的情况下才考虑换相。
采用三进制的编码可将多维数组转换为一个三进制整数,使得每个可行解对应一个整数,整数的取值范围是所有的可行解。然而粒子群算法的求解结果是十进制实数。因此,需在这两者之间设置一个合适的转换规则。转换规则设置如下:在求目标函数值之前,对粒子群算法每次的运算结果(即粒子群的位置,为十进制实数)进行取整,且对越限的情况进行处理(越限情况下的解为不可行解),然后将十进制整数转换为三进制(转换为三进制的目的是为了求目标函数),之后再按照基本的粒子群算法处理。其中为了得到较为精确的结果,采用如下的取整方法:先求出计算结果所在的最小整数区间,然后比较区间端点的目标函数值,取较小的值所对应的整数作为结果。如实数1.5所在最小整数区间为[1,2],分别计算目标函数值f(1)和f(2),假如f(1) 图3 粒子群算法流程图 设某台区的表箱数为40,且均为单相用户。台区的负荷数据如表1所示。表中提供的数据有负荷编号、负荷大小(电流)、功率因数及负荷当前所处的相别。按负荷的大小可将该台区的用户可分为3类:第一类(编号1~5)为大用户,第二类(编号6~35)为普通用户,第三类为小用户(36~40)。在40个用户中,任意选取11个用户安装换相开关,这些用户在表1中以星号的形式标注。由于三相负荷假定是平衡的,所以不考虑三相负荷。 图4是换相前后的三相电流波形,从该波形图上可以直观地看出经过换相调整后,三相电流达到了大致的平衡,电流的大小接近于相等,在相位上相差接近于120°。图5是优化过程目标函数值的变化曲线。该图的横坐标是进化代数,纵坐标是目标函数值。随着进化代数的增加,目标函数值逐渐减小,直到达到最小值16.3649为止,与用枚举法(也是以三进制的形式编码,逐一检查可行解是否是最优解)求得的结果相符合,说明求得的结果不是局部最优解。 如图6所示,相比于枚举法,粒子群算法的计算时间更短(粒子群算法平均为4.9s,枚举法为68.0s),准确率较高(达到80%),因此粒子群算法具有一定的可行性。 实际中应根据求解问题的复杂程度选择合适的算法。比如在换相开关的数量不是特别多的情况下,采用枚举法在保证100%准确的同时,在求解的时间上也和粒子群算法相差无几(如图7所示,在10个换相开关的情况下枚举法计算时间6.76s,粒子群算法计算时间为4.45s)。而在换相开关较多的场合采用枚举法显然不太合适(如本例中的情况)。因为采用枚举法虽然可以保证得到最优的解,但求解的时间相对较长,而粒子群算法则通过降低准确率换取求解速度的增加,在两者之间达到较好的平衡。因此,实际中根据问题的复杂程度可能对准确率和求解时间有不同的侧重,应据此选择合适的算法。 表1 台区单相用电负荷数据 注:1.表中标*号的表示换相支路;2.表中的负荷支路是未经过排序的结果 图4 换相前后三相电流波形图(上图是换相前的波形,下图是换相后的波形) 图5 优化过程目标函数值的变化 图6 算法性能对比 图7 不同换相开关数目下两种算法的运算时间对比 三相负荷平衡的调整过程实质上是通过调整某些负荷的相别使得三相负荷不平衡度最小的优化过程。本文采用三进制编码的方法可以使得换相开关的最优换相调整问题从原来的多维问题转换成一维问题,避免造成“维数灾”。由于求解的问题是整数规划问题,因此在求目标函数之前对粒子群的位置进行取整、越限处理及十-三进制转换以适应三相不平衡负荷换相问题的求解需要。算例结果表明,本文提出的方法比枚举法的求解时间更短,且算法的准确率可达到80%以上,具有一定的可行性。 [1] 张弘廷.低压降损的金钥匙——就地平衡降损法[M].中国电力出版社,2003. [2] 方恒福,盛万兴,王金丽,等.配电台区三相负何不平衡实时在线治理方法研究[J].中国电机工程学报,2015,(9):2185-2193. [3] 傅军栋,喻勇,刘晶,等.低压配电网三相不平衡节能算法研究[J].华东交通大学学报,2014,(3):110-114,136. [4] 张明,谢珊珊,罗云峰,等.低压配电网三相负荷不平衡优化模型的研究[J].武汉科技大学学报(自然科学版),2015,(1):59-62. [5] 钱锋.粒子群算法及其工业应用[M].科学出版社,2013. [6] 林海雪.电力系统的三相不平衡[M].中国电力出版社,1998. [7] Kennedy J,Eberhart R.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neutral Networks,1995:129-132. [8] Kennedy J,Kennedy J F,Eberhart R C,et al.Swarm intelligence[M].Morgan Kaufmann,2001. [9] 崔志华,曾建潮.微粒群优化算法[M].科学出版社,2011.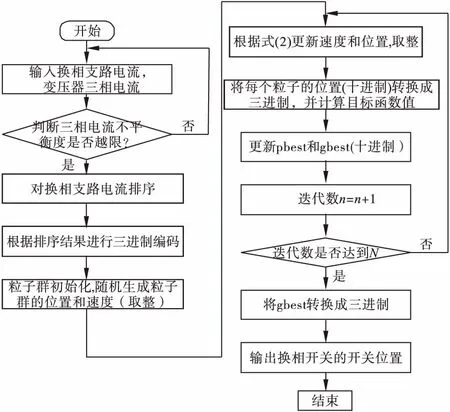
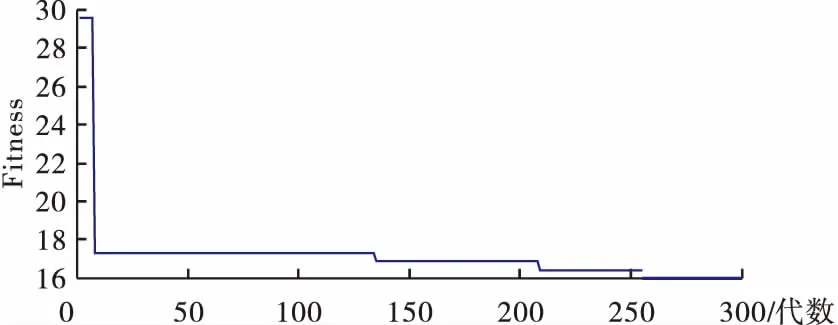
4 算例




5 结论
