建模思想在“数学分析”教学中的应用
2017-03-13张文丽张燕霞
张文丽,张燕霞
(长治学院 数学系,山西 长治 046011)
建模思想是对实际问题通过借助数学的理论知识和方法,构建一个合理的数学模型,从而来解决实际问题。是加强数学与生产实际和专业的紧密联系,培养学生发现问题、分析和处理实际问题的数学应用意识、应用能力和创新意识与能力的一种思想方法[1]。
一、建模思想在人才培养方面的重要性
当今社会需要将所学到的理论知识应用到实际生活中,能够推动科技与社会不断进步的应用型人才[2]。1992年,教育部高等教育司和中国工业与应用数学学会共同主办全国大学生数学建模竞赛,这个竞赛针对全国高等院校的任何专业的所有学生,在举办竞赛的十几年来,以25%以上的年增长迅速发展,迄今为止,这是大学生参加的所有的竞赛中规模最大,影响最广,意义最深的。这个竞赛不仅得到了社会各界的认可,所获得的奖项也常作为用人单位衡量一个人水平的标准[4]。数学建模的比赛形式也是多种多样,有中国数学建模网络挑战赛、中国数学建模国际赛以及地区赛等。这足以表明建模思想对于人才培养的重要性。通过数学建模不但可以提升理解、分析及处理问题的能力,还可以鞭策学生学习的主动性,以及对于计算机的应用,提高对于知识理论的应用与创新的能力。将实际的问题转化为专业的知识理论进行解决。许多高校每年都鼓励学生利用寒暑假参加社会实践活动,主要是培养学生利用所学理论知识解决实际问题的能力,将来能够更好地适应社会,服务社会。因此,建模思想就是一座将理论与实际相结合的无形桥梁。
二、建模思想在“数学分析”教学中的应用
“数学分析”课程的特点是理论性强、逻辑性强、应用性弱。应用性仅在积分理论中有所体现,且主要体现在了空间几何与物理学中,而这些知识内容与实际生活严重脱节,较陈旧。在教学过程中,教师着重强调定理和公式的证明及推导[5],解题方法的分析,淡化对数学分析中概念的背景和实质、概念与概念间的联系及理论知识的应用的讲解,致使学生仅仅掌握了一些抽象的理论知识,对如何应用所学知识处理实际问题却一窍不通,更对怎样应用无法下手。最终导致学生的学习兴趣越来越低,学习效果也逐渐降低。
(一)引入生动实例,渗透建模思想
为了使学生真正认识并切身体会数学分析在实际生活中的应用,从而认识到学习数学分析的重要性,发现其所蕴含的数学美,提高学生对数学分析学习的兴趣且提升学习效率,成为社会所需的应用型人才,在教学过程中教师应该有意识地渗透建模思想,引导学生将所学的理论与实际生活相结合。如在讲函数的最大值最小值问题时可以举下列与实际生活紧密联系的例子,有意识地渗透建模思想。
例1[9]假设某工厂生产x千件的成本是C(x)=x3-6x2+15x,售出该产品x千件的收入是r(x)=9x。问是否存在一个能取得最大利润的生产水平?如果存在的话,找出这个生产水平。
解:根据题意可以建立数学模型,即售出x千件产品的利润是
p(x)=r(x)-C(x)
然后利用数学分析中极值理论来判断,得出当x=3.414存在一个能取得最大利润的生产水平。
再比如,讲有限极值这一节时,可以举如下例子:
例2[10]某化工厂生产A1,A2,A3,A4四种化工产品,每种产品生产1吨所消耗的工时、能源和获得的利润见下表。
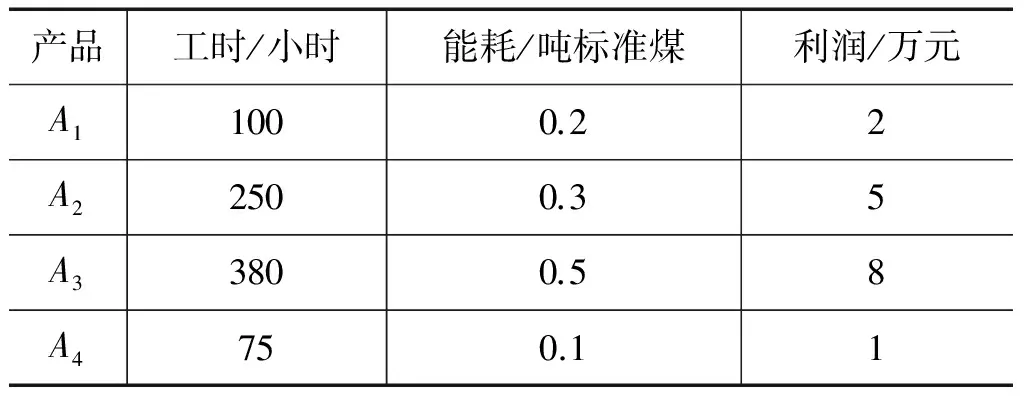
生产1吨产品的消耗与收益
已知该厂明年的工时为18 480小时,能耗为100吨标准煤,欲使该厂明年的总利润最高,请确定各种产品的生产数量。
解:设该厂全年生产A1,A2,A3,A4四种产品的数量分别为x1,x2,x3,x4,总利润为z,则可以建立数学模型:
z=2x1+5x2+8x3+x4
条件为
100x1+250x2+380x3+75x4=18 480
0.2x1+0.3x2+0.5x3+0.1x4=100
接着利用数学分析中的隐函数组存在定理和条件极值理论,借助matlab软件求出各种产品的生产数量分别为x1=x2=x3=x4=0,x3=48.631 6时总利润最大为z=389.052 6。
再如,在有关极限的定义的教学中引入著名的“割圆术”或者是利用现有的教学软件[6]——超级画板向学生展示在坐标中一条曲线上的点的变化,使学生理解极限的定义以及演示其形成过程,这样不仅花费的学习时间少,而且取得的效果非常好。在讲解函数的连续性的基本性质时,可以利用在不平的地面上放椅子,椅子能否放稳[7]的问题让学生进行建模,培养学生将实际问题转化为数学问题的能力,不仅可以进一步理解并加深与巩固所学的理论知识,而且还可以培养实际应用能力,增强学习兴趣。在讲导数时,可以选择与实际生活密切相关的经济问题来讲解。例如证券的利息率问题,存款与贷款问题,线性规划问题,风险决策问题等。在讲解积分定义时,可以先回忆圆的面积公式的来源,规则的梯形的面积,然后由易到难的引导学生,利用极限的思想,通过三步“近似、求和、取极限”求出解曲边梯形的面积,从而推出定积分的定义。在积分理论知识方面可以举有关通讯卫星的覆盖面积的数学模型,或有关物理学中的交流电的有效值的数学模型,或计算房间中关于灯泡的最佳高度的模型来进行讲解[5]。对于级数的定义,级数的收敛性以及级数的实际应用的讲解中,我们可以使用传说中跑的最快的人阿基里斯与乌龟赛跑的悖论问题[8],由此巧妙地引入级数的基本概念,这样在学习级数时就可以将原本抽象的、枯燥的内容变得生动有趣,使学生通过实际问题感受到理论知识中所蕴含的数学美。激发学生对学习的热情,提高学生的应用能力。这样巧妙地在教学中融入建模思想不仅可以使学生有效地掌握所学的知识,还可以将知识应用到生活当中,在学习中找到乐趣,提高学习的效率,让学生了解数学分析中的那些枯燥乏味的定理以及有关的推广是来源于我们的现实生活之中,并不是凭空得来的,都有其应用背景。数学分析中的大部分内容是后继的许多学科的基础,这样可以为后续的学习打下坚实的基础。除此之外,再结合现代的计算机软件,例如:Maple、Matlab等,使学生能够了解概念的产生过程,真正把握与理解其内涵,不用对概念进行死记硬背,从而增强学生学习的自信心,提高学生对于理论知识学习的兴趣。
(二)借助建模比赛,加强建模训练
教师也可以通过对每年的全国建模问题进行分析,然后借助比赛问题对学生所学的相应知识进行深入的讲解。例如在讲解极值的相关知识时,就可以借用2006年的全国性数学建模比赛C题——有关易拉罐形状与尺寸的最优设计,处理这个问题就需要熟练地掌握数学分析中的有关极值的讨论与计算,并以Maple、Matlab更加直观、具体地来进行绘图与计算。还有2010年A题,关于输油管的设计方案问题,将其转化为多元函数的最值以及驻点的求解,并且借助Matlab进行数值计算。
通过在数学分析中渗透建模思想,可以将枯燥的理论知识与实际生活紧密结合,将实际问题转化为数学问题来解决。这样不仅可以培养并提高学生的数学素质,还可以加强学生的动手与动脑能力,通过学生自己对于知识的深入挖掘,激发其求知欲。这对于当今社会所需的应用型人才的培养有很大的帮助。
[1]毕晓华,徐钧.将数学建模思想融入应用型本科数学教学初探[J],教育与职业,2011(9).
[2]陆英杰,娄华,马春全,邓桦,卢玉葵.改革专业教学与社会人才需求的对接[J],科技信息,2010(5).
[3]李辉,王艺霏,刘一鋆,张丽春.数学建模思想渗透到数学教学中的地位与作用[J],吉林农业科技学院学报,2013(1).
[4]李娜.数学建模与大学生创新能力的培养[J].榆林高等专科学校学报,2014(4).
[5]李声峰,张裕生,梅红.将数学建模思想融入《数学分析》课程教学的探索与实践[J].赤峰学院学报(自然科学版),2011(7).
[6]牛英春.数学建模思想在《数学分析》教学中的应用[J].开封教育学院学报,2015(6).
[7]王杉林.经营类院校数学建模课程教学体系改革研究初探[J].教育教学论坛,2015(6).
[8]孙业国.数学分析中极限概念的教学策略与研究[J].淮南师范学院报,2013(3).
[9]同济大学数学系.高等数学:上册[M].北京:高等教育出版社,2014.
[10]史明霞,等.新编工程数学[M].大连:大连理工大学出版社,2012.
