极地运输船波浪载荷计算分析

崔兵兵 王淑平 赵家蛟

（上海船舶研究设计院，上海201203）

0 前言

随着全球气候变暖，北冰洋正在加速融化，最新预测显示，北冰洋很快将出现夏季无冰年，从而打通连接欧洲、北美东部和东亚地区新的海上航运通道，将极大地缩短航行距离和时间。考虑到航线的特殊性，计算和分析极地航行海区下船体的波浪诱导载荷长期值，对船体结构的设计很有意义。

对于常规船舶，船体梁载荷可依照规范公式计算，而本文要研究的极地甲板运输船，L/B=4.7，B/D=5.7，超出规范船体梁波浪载荷计算公式的适用范围，需要采用直接计算的方法来进行分析。

本文基于谱分析方法，采用WASIM水动力分析软件计算2个工况、24个浪向角和26个周期下的波浪诱导载荷，获得其船中剖面垂向弯矩的幅频响应函数，并采用SESAM软件Postresp模块结合具体的波浪谱和目标船航行的东北和西北航道所经10个海区波浪散布图进行长期预报，进而获得船体各个海区下船中剖面垂向弯矩的长期值，比较分析计算结果。

1 基于谱分析的波浪诱导载荷长期预报方法

谱分析方法被认为是最精确的，建立在真实的海况、装载的基础上，涉及复杂的水动力计算。该方法不针对某特定船型，而是对各种在海浪中航行的船舶都适用，是一种较为完善的计算方法。

1.1 谱分析方法理论基础

谱分析方法的理论基础是随机过程理论中的线性系统变换［1］。对于船舶与海洋工程结构物这一典型的线性动力系统，其变换关系可用图1表示。

图1 线性系统变换关系图

其中：η（t）为作用在船体上的波浪过程（系统的输入）；X（t）为由于波浪作用引起的船体运动或载荷过程（系统的响应）。系统的响应过程与输入过程之间的关系见式（1）：

式中：L——线性算子，通过其可将η（t）变换成X（t）

在船舶运动和载荷分析中，设 Gηη（ω）和 GXX（ω）分别为平稳正态随机波浪过程η（t）和波浪诱导载荷交变过程X（t）的功率谱密度函数，则由随机过程理论可知式（2）：

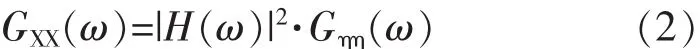
式中：H（ω）——幅频响应函数；

Gηη（ω）——波浪的功率谱密度函数；ω——波浪圆频率，rad/s

1.2 波浪诱导载荷长期分布的预报

求解获得波浪诱导载荷幅频响应函数后，结合具体的波浪谱和海况散布图就可以进行波浪诱导载荷长期分布的预报。

波浪谱密度函数一般选取国际船模水池会议（ITTC）推荐使用的双参数的Pierson-Moskowitz谱（以下简称 P-M 谱）［2］。 其表达式见式（3）：

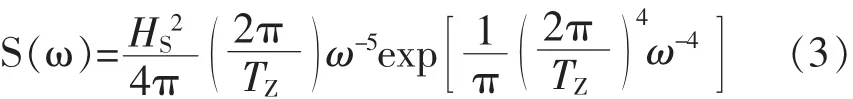
式中：HS——有义波高，m；

TZ——平均过零周期，s；

ω——波浪圆频率，rad/s；

S（ω）——波浪谱密度函数，m2·s

由幅频响应函数和波浪谱密度函数，可从式（4）得到响应谱密度函数：

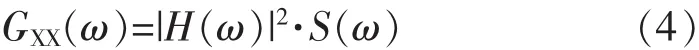
考虑到短期海况下波浪运动是平稳窄带过程这一假设，对于船波构成的线性系统，波浪诱导载荷的交变响应的峰值服从Rayleigh分布，概率密度函数，见式（5）：

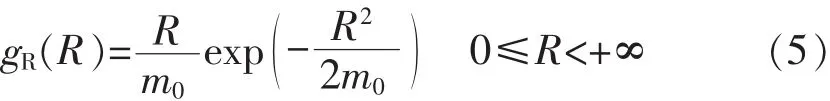
式中：R——波浪诱导载荷响应峰值；

m0——功率谱密度GXX（ω）的零阶矩

进而，可得到波浪诱导载荷响应峰值的分布函数，见式（6）：

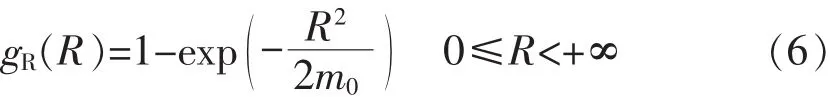
为得到波浪诱导载荷在给定时间内的循环次数，需要给出波浪诱导载荷交变响应过程的平均跨零率υ，即单位时间内以正斜率跨越零均值的平均次数。其表达式见式（7）：

在计算波浪诱导载荷响应平均跨零率时还要用到响应谱的2阶矩，波浪诱导载荷的功率谱密度函数 gR（R）的 n 阶矩计算通式见式（8）：

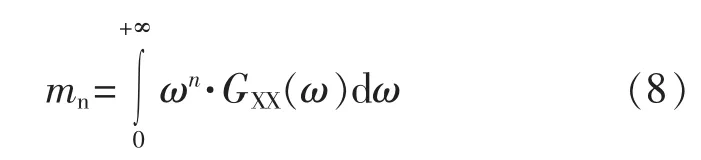
选定的海况分布资料，可获得海况出现的概率。对于某一给定海况，船舶可能以任意航向航行，计算中可划分nH个航向，并假定各个航向出现的概率相等。波浪诱导载荷的长期分布可表示为各短期分布的加权组合。其分布函数见式（9）：

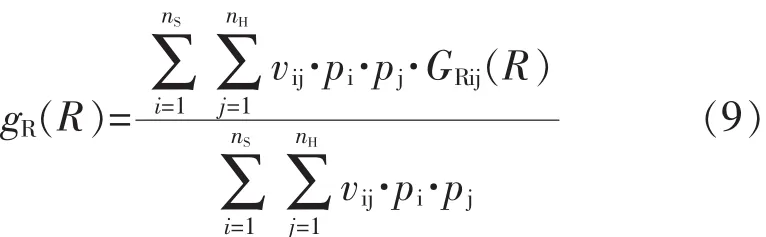
式中：nS——海况分布资料中的海况总数；

nH——划分的航向总数；

vij——海况i和航向j下，波浪诱导载荷的平

均过零率，由式（7）计算；

pi——第i个海况出现的概率，取为海况分布

资料中各海况出现的频率；

pj——第j个航向出现的频率

2 全球波浪散布图统计与分析

2.1 理论基础

海区波浪散布图有义波高概率密度函数的计算如式（10）所示，服从三参数 WEIBULL 分布［3］：

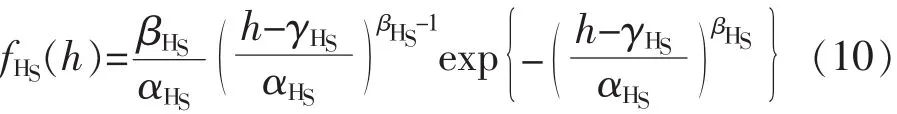
式中：h——有义波高，单位m；

αHS，γHS——WEIBULL分布参数，全球104个不同的海区（如图2所示）对应取值［3］

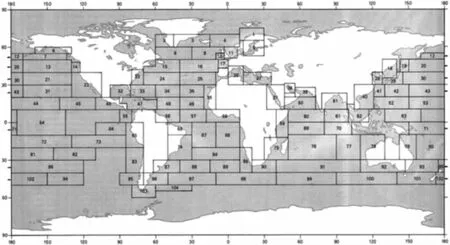
图2 全球海区分布图

平均跨零周期概率密度函数的计算如式（11）所示服从对数正态分布：

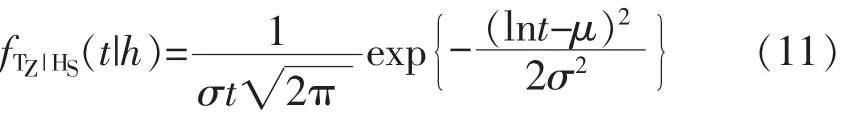
式中：t——平均跨零周期；

μ，σ——对数正态分布参数，可按式（12）～式（13）计算：

式中：不同的海区，a1、a2、b1、b2对应不同的取值［3］

2.2 波浪散布图统计程序的算法

2.2.1 概率密度函数计算

对于特定的海区，可获得WEIBULL分布参数αHS、γHS，从 0 m 到最大的有义波高值 hmax，取有义波高的步长为Δh，依据式（10）计算出不同有义波高下的概率密度 fHS（h）。

对于特定的海区，可获得对数正态分布参数μ、σ的相关计算参数，从0.05 s到最大的平均跨零周期 tmax，取平均跨零周期的步长为 Δt，依据式（11）计算出给定有义波高h，不同平均跨零周期下的概率密度 fTZ|HS（t|h）。

2.2.2 概率分布函数计算

1）有义波高概率分布函数计算。对于短期海况（hs，tz），以 hs为中间值的区间（hs-Δh，hs+Δh）有义波高概率分布函数应按式（14）计算。

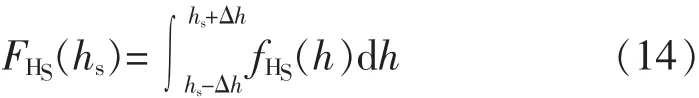
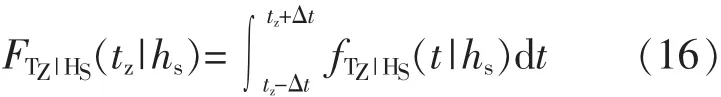
这里采用梯形法计算获得，如式（17）所示。

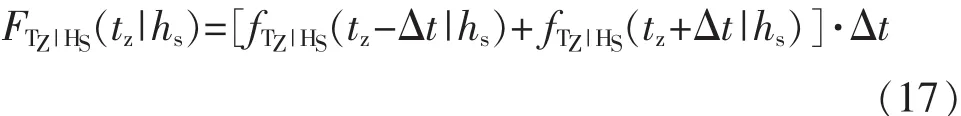
2.2.3 短期海况出现概率计算

短期海况（hs，tz）出现的概率应按式（18）计算。

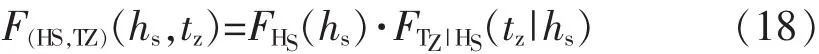
这里为了使特定海区所有海况出现的概率之和为 1，对于式（18）做了如下调整，见式（19）：

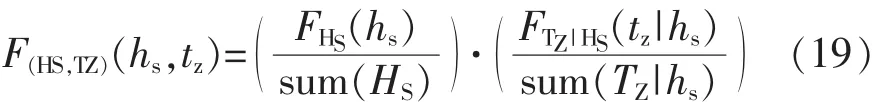
这里采用梯形法计算获得，如式（15）所示。

FHS（hs）=［fHS（hs-Δh）+fHS（hs+Δh）］·Δh （15）

2）特定有义波高下，平均跨零周期概率分布函数计算。 对于短期海况（hs，tz），hs有义波高下以 tz为中间值的区间（tz-Δt，tz+Δt）平均跨零周期概率分布函数应按式（16）计算。

式中：sum（HS）——特定海区所有海况有义波高概

率之和，按式（20）计算：

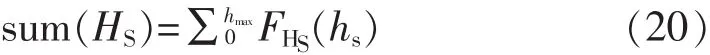
式中：sum（TZ|hs）——特定海区hs有义波高下所有海况平均跨零周期概率之和，按式（21）计算

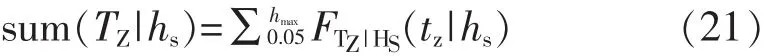
2.3 波浪散布图统计程序的运行

2.3.1 输入文件

1）WEIBULL分布和对数正态分布参数文件。文件中包含不同海区对应的Weibull分布αHS、γHS参数取值［3］，不同海区对应的对数正态分布 a1、a2、b1、b2参数取值［3］，如图 3 所示。

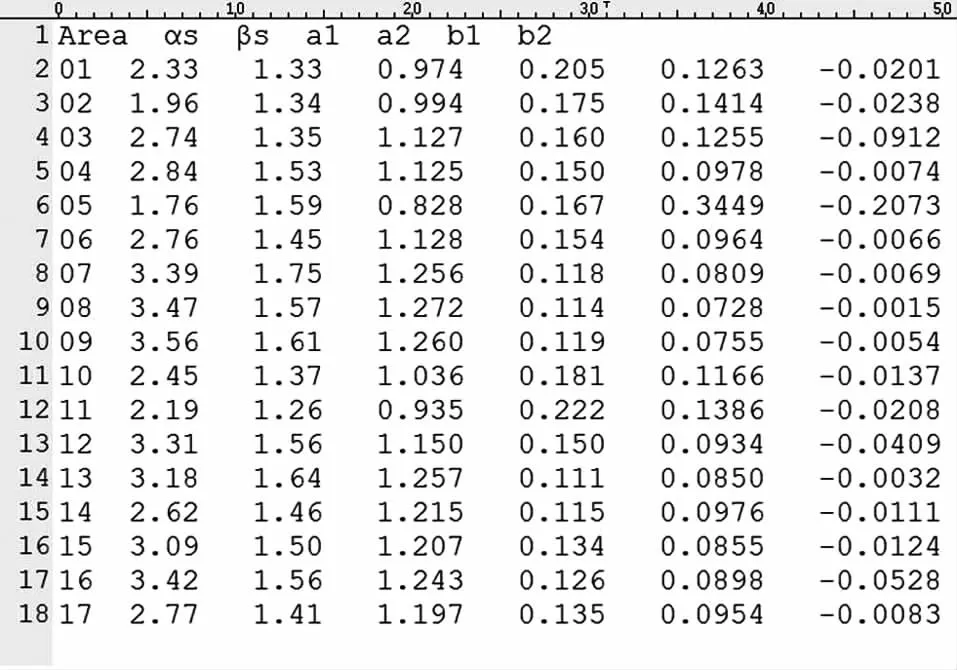
图3 WEIBULL分布和对数正态分布参数

2）有义波高参数文件。文件中包含输出波浪散布图有义波高的个数和对应的取值，如图4所示。

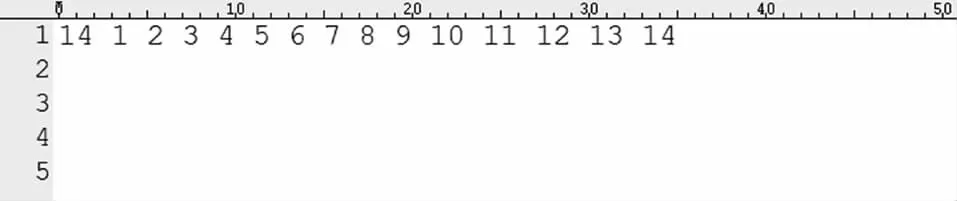
图4 有义波高参数

3）平均跨零周期参数文件。文件中包含输出波浪散布图平均跨零周期的个数和对应的取值，如图5所示。

图5 平均跨零周期参数

4）有义波高区间范围参数文件。文件中包含输出波浪散布图有义波高区间，用来定义2.2.2节中有义波高概率分布函数的积分区间，如图6所示。

图6 有义波高区间范围参数

5）平均跨零周期区间范围参数文件。文件中包含输出波浪散布图平均跨零周期区间，用来定义2.2.2节中平均跨零周期概率分布函数的积分区间，如图7所示。

图7 平均跨零周期区间范围参数

2.3.2 程序窗口

从图2中选取并键入要计算的海区编号（范围从1到104），如海区编号为40，程序的运行窗口如图8所示。

2.3.3 输出文件

通过程序的内部算法计算，获得海区40对应的波浪散布图文件，如图9所示。

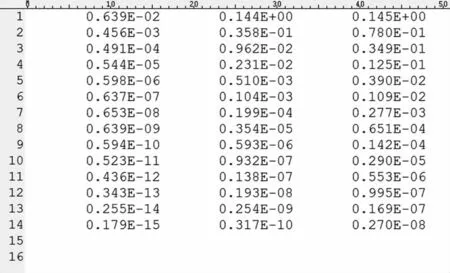
图9 波浪散布图文件

3 目标船主尺度和计算参数

3.1 目标船主尺度

本文要研究的目标船为极地甲板运输船，主尺度如下：

3.2 相关计算参数

3.2.1 计算工况

本文选取目标船满载（LC1）和压载（LC2）这2个典型的工况（如表1所示），进行水动力分析。

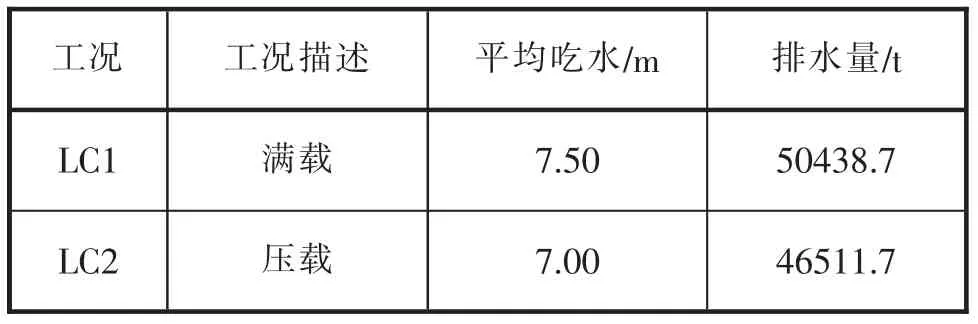
表1 计算工况

LC1工况的重量分布曲线如图10所示，LC2工况的重量分布曲线如图11所示。

3.2.2 浪向和周期

波浪入射角范围取0°～345°，间隔15°，共24个；波浪周期从5～30 s取值，间隔1 s，共26个。

3.2.3 超越概率和海浪谱

本文在进行波浪诱导载荷的长期预报时选取10-8超越概率［4］。

海浪谱采用ITTC推荐的双参数P-M谱。

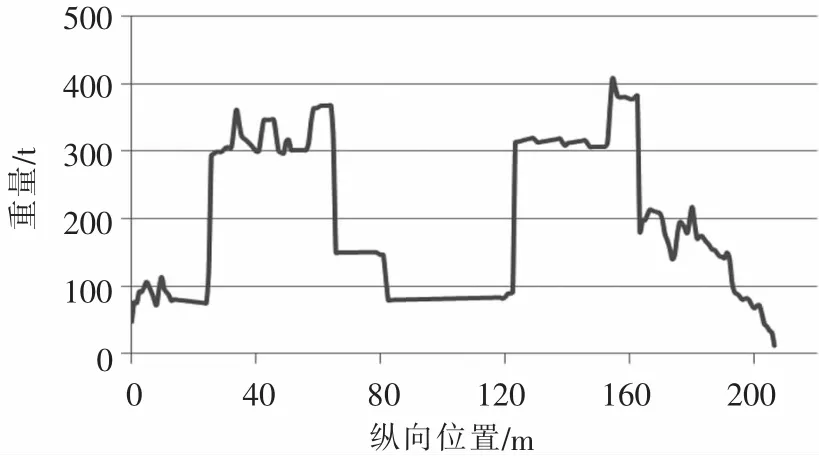
图10 LC1工况的重量分布曲线

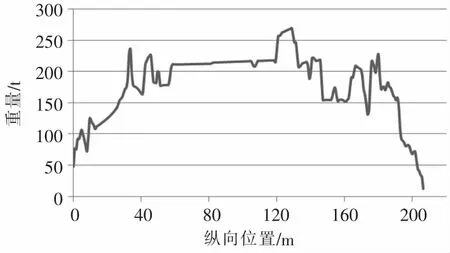
图11 LC2工况的重量分布曲线

3.2.4 波浪散布图

对于船舶在使用期间内的波浪载荷进行直接计算，选择波浪散布图时，需要考虑船舶的具体航行海区［4］。

目标船航行航道有两条：东北航道西起摩尔曼斯克港，经巴伦支海、喀拉海、拉普捷夫海、东西伯利亚海、楚科奇海至白令海到符拉迪沃斯托克（海参崴），途经 18、19、20、12、1 海区；西北航道东起巴芬湾，西至波弗特海，途经 11、4、3、8、2 海区。

文中目标船航行海区的波浪散布图通过第2章介绍的程序统计获得。同时选取了北大西洋波浪散布图［4］，以比较波浪诱导载荷长期值。

4 实船水动力分析

4.1 目标船水动力模型

通过导入船体外壳横剖面型线并设置适当的网格控制参数，WASIM软件将自动划分船体湿表面水动力网格。与其他商用水动力计算软件不同的是，WASIM软件采用的RANKINE源法，需要划分自由面水动力网格。水动力模型如图12所示。

4.2 计算剖面选取

在本文的波浪载荷计算中，沿目标船的船长方向共选取了20个计算剖面，各剖面的纵向位置，如表2所示。

图12 水动力模型

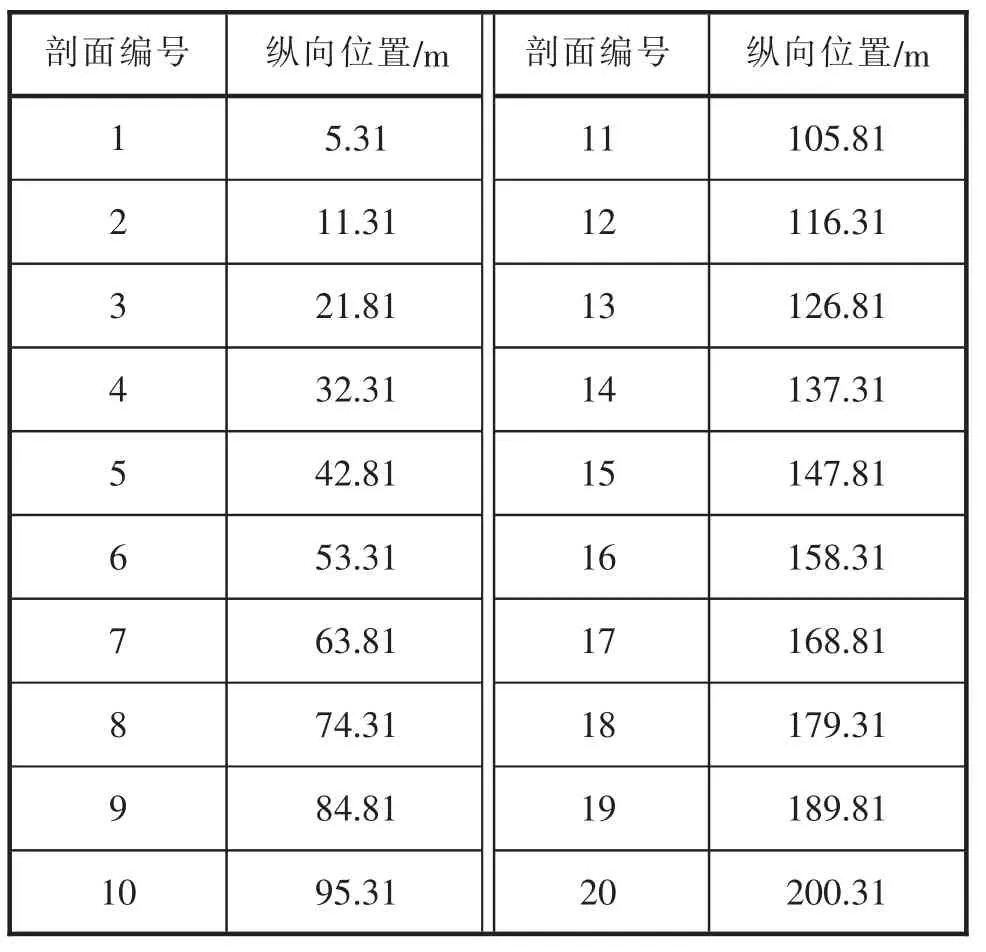
表2 计算剖面的纵向位置

4.3 垂向波浪剪力长期预报

北大西洋和东北航道波浪散布图下：LC1工况垂向波浪剪力长期值沿船长分布曲线如图13所示；LC2工况垂向波浪剪力长期值沿船长分布曲线如图14所示。

北大西洋和西北航道波浪散布图下：LC1工况垂向波浪剪力长期值沿船长分布曲线如图15所示；LC2工况垂向波浪剪力长期值沿船长分布曲线如图16所示。

4.4垂向波浪弯矩长期预报

北大西洋和东北航道波浪散布图下：LC1工况垂向波浪弯矩长期值沿船长分布曲线如图17所示；LC2工况垂向波浪弯矩长期值沿船长分布曲线如图18所示。

北大西洋和西北航道波浪散布图下：LC1工况垂向波浪剪力长期值沿船长分布曲线如图19所示；LC2工况垂向波浪剪力长期值沿船长分布曲线如图20所示。

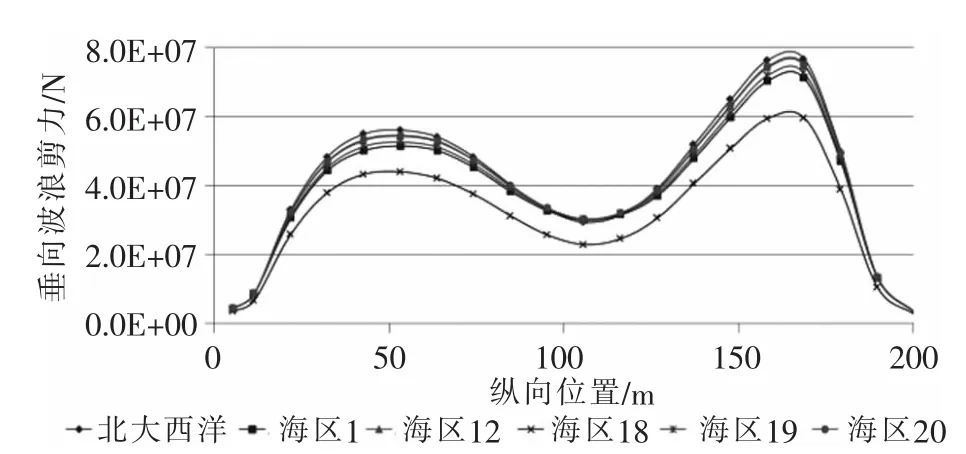
图13 垂向波浪剪力长期值沿船长分布曲线（LC1）

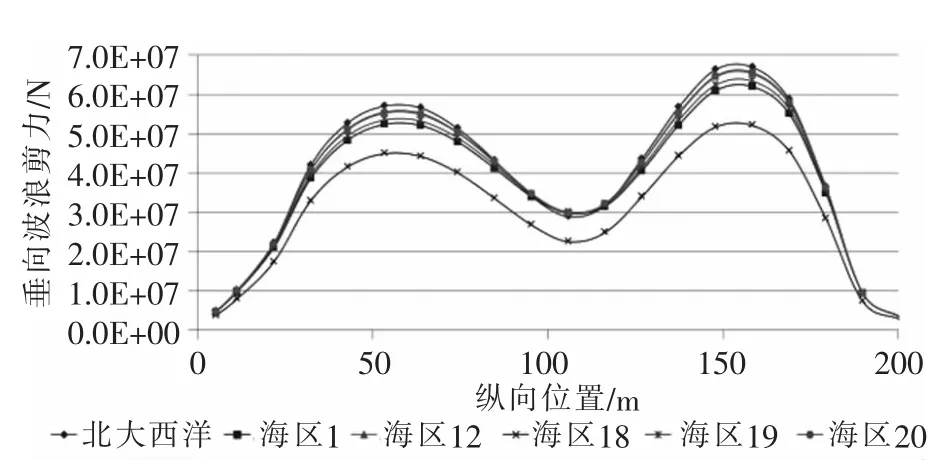
图14 垂向波浪剪力长期值沿船长分布曲线（LC2）

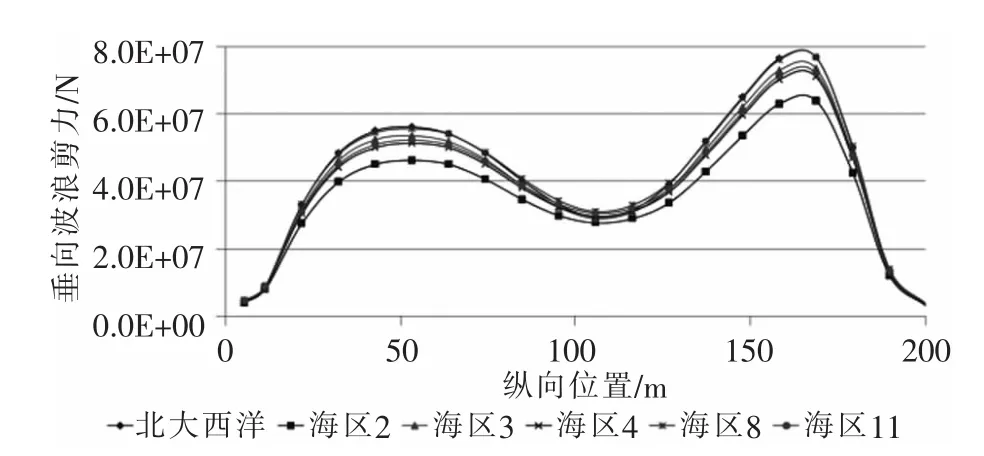
图15 垂向波浪剪力长期值沿船长分布曲线（LC1）

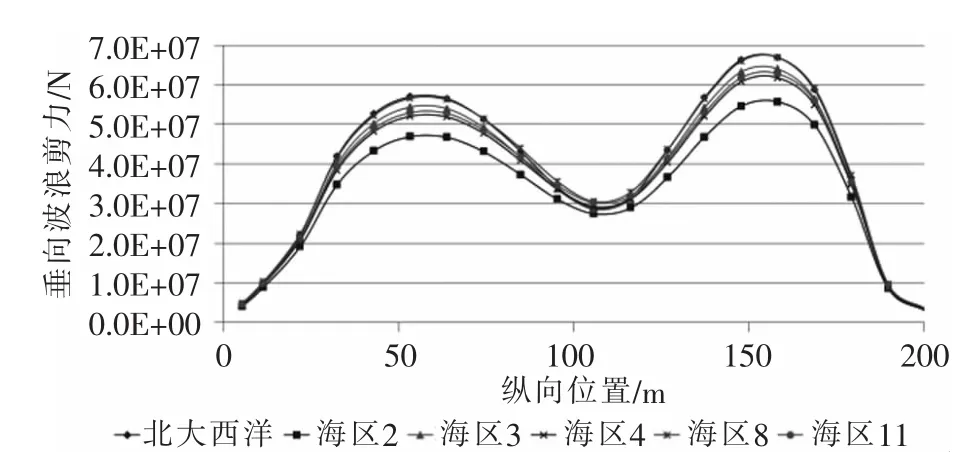
图16 垂向波浪剪力长期值沿船长分布曲线（LC2）

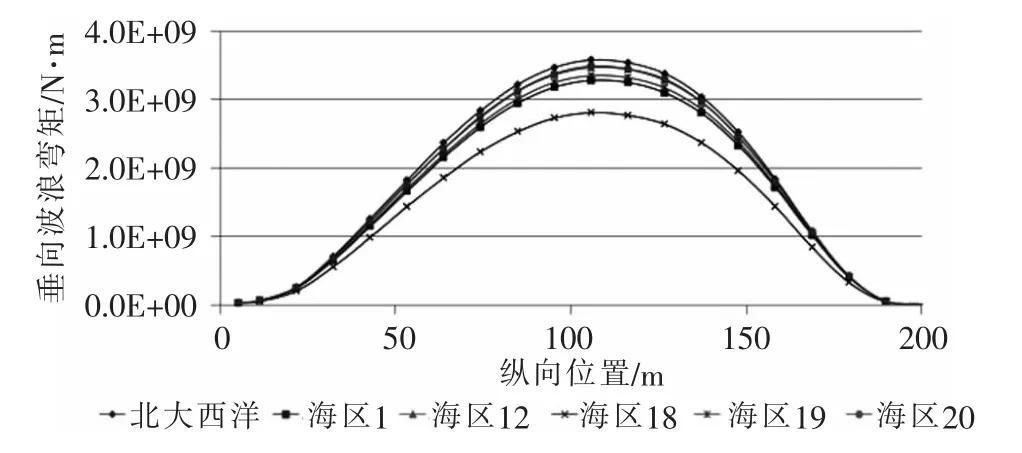
图17 垂向波浪弯矩长期值沿船长分布曲线（LC1）

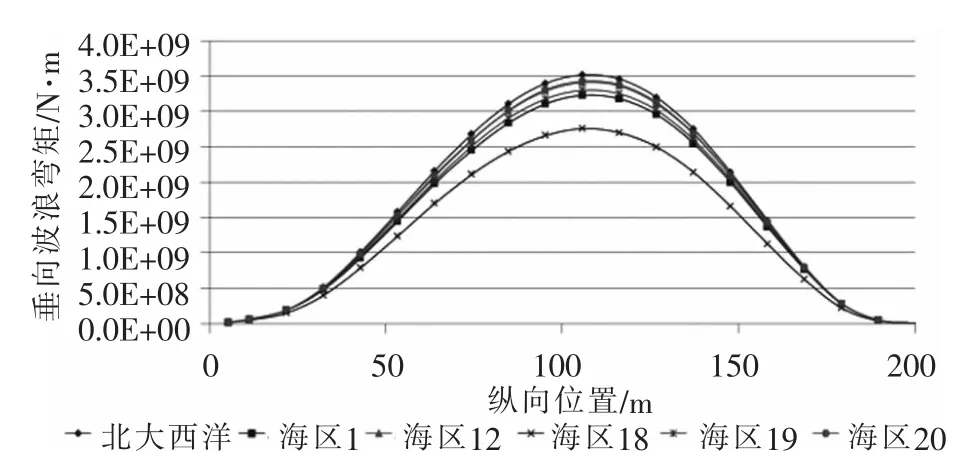
图18 垂向波浪弯矩长期值沿船长分布曲线（LC2）

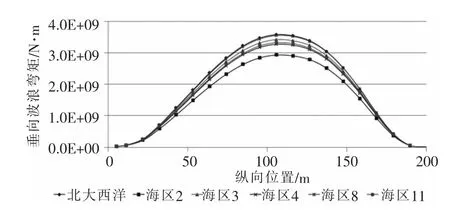
图19 垂向波浪弯矩沿船长分布曲线（LC1）

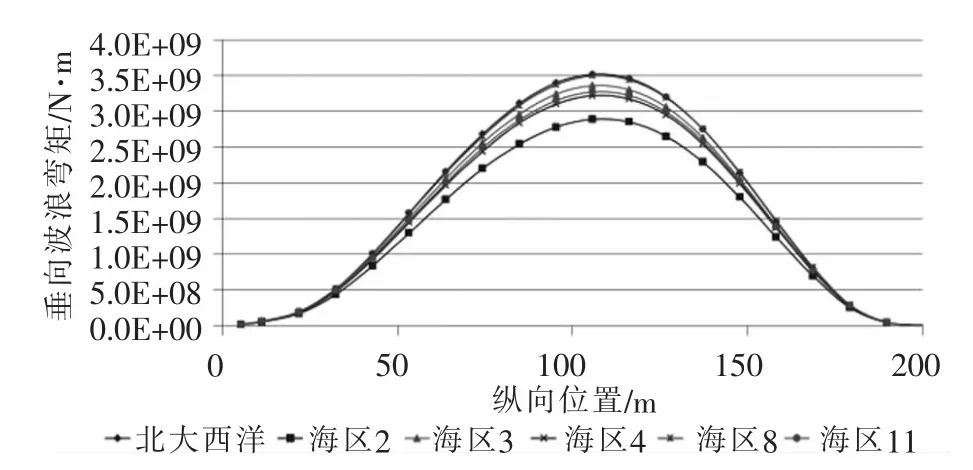
图20 垂向波浪弯矩沿船长分布曲线（LC2）

4.5 船中垂向波浪弯矩长期值比较

目标船LC1与LC2工况北大西洋和东北航道下各海区船中11号剖面垂向弯矩长期预报结果见表3。

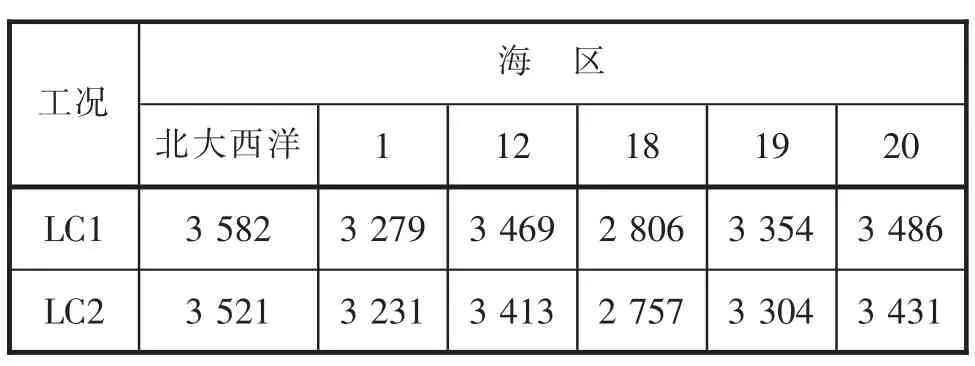
表3 船中剖面载荷长期预报（东北航道）MN·m

通过分别比较LC1与LC2工况北大西洋和东北航道下各海区船中11号剖面垂向弯矩长期预报结果可以发现：两个工况东北航道下各海区的预报值均小于北大西洋海区。

目标船LC1与LC2工况北大西洋和西北航道下各海区船中11号剖面垂向弯矩长期预报结果见表4。

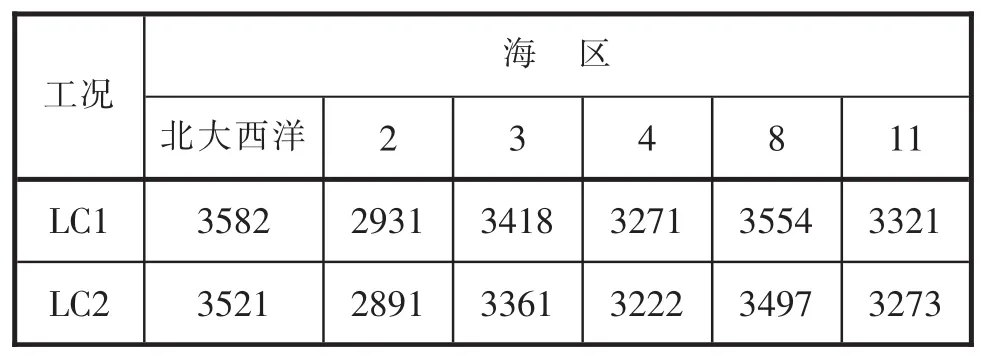
表4 船中剖面载荷长期预报（西北航道）MN·m

通过分别比较LC1与LC2工况北大西洋和西北航道下各海区船中11号剖面垂向弯矩长期预报结果可以发现：两个工况西北航道下各海区的预报值均小于北大西洋海区。

5 结语

1）采用FORTRAN语言编写全球波浪散布图统计与分析程序。该程序可在减少人为数据操作的前提下，快速准确地统计和分析全球各海区的波浪散布图。

2）基于谱分析方法，并结合具体的波浪谱和程序统计分析得到的特定海区波浪散布图，计算获得了船体各个海区下沿船长分布的垂向波浪剪力和垂向波浪弯矩的长期值。这为后续船体结构的设计和强度分析提供了载荷基础。

3）通过比较分析LC1与LC2工况下，目标船船中剖面北大西洋海区下垂向波浪弯矩长期值均大于东北、西北航道下各海区的长期值。由此可知，对于本文要研究的极地航道航行船舶，若在船体结构设计时选取北大西洋海区对应的载荷是偏于安全的。

［1］冯国庆.船舶结构疲劳评估方法研究［D］.哈尔滨：哈尔滨工程大学，2006.

［2］PIERSON W J，MOSKOWITZ L.A proposed spectral form for fully developed seas based on the similarity theory of S.A.Kitaigorodoskrii［J］.Journal of Geophys.Research，1964（24）：5181-5190.

［3］DNVGL society.DNV-RP-C205-Environmental conditions and environmental loads［S］.2010.

［4］戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京：国防工业出版社，2007.