基于云模型的四川盆地气候变化时空分布特征分析

高蔺云, 黄晓荣，2, 奚圆圆, 李晶晶, 马凯

(1.四川大学 水利水电学院,四川 成都 610065;2.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065)

基于云模型的四川盆地气候变化时空分布特征分析

高蔺云1, 黄晓荣1，2, 奚圆圆1, 李晶晶1, 马凯1

(1.四川大学 水利水电学院,四川 成都 610065;2.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065)

为了研究四川盆地气候变化的时空分布特征,利用1955—2010年四川盆地内15个气象站的月降水量和月气温资料,使用高桥浩一郎蒸发公式计算月蒸发量,采用云模型描述降水量、气温和蒸发量在时间上分布的特性,运用Kendall秩次相关法分析降水量、气温和蒸发量的时空分布特征。结果显示:1955—2010年的四川盆地年度及季度降水量序列中,冬季平均降水量分布最不均匀,秋季次之;年度及季度气温序列中,冬季平均气温分布最不均匀,且最不稳定,秋季平均气温分布最稳定;年度及季度蒸发量序列中,冬季平均蒸发量分布最不均匀,多年平均蒸发量序列分布最均匀;年度及季度降水量均呈下降趋势;年度及季度气温中除夏季平均气温呈下降趋势外,其余均呈上升趋势;年度与秋季蒸发量呈下降趋势,春、夏、冬3个季节的平均蒸发量呈上升趋势。对四川盆地气候变化时空分布特征的分析，可为该地区的气候变化研究提供参考与技术支持。

四川盆地；气候变化;云模型;Kendall秩次相关法；降水量；气温；蒸发量

近年来,随着全球气候的变暖,极端天气气候事件发生的强度和频率有所增加[1-2],对人类生活和自然生态系统均造成了巨大的威胁。因此,了解气候变化特征,对水资源的管理以及人类生命财产安全的保护有着至关重要的作用。王会军院士[3]指出,自20世纪80年代开始,世界气候研究大规模兴起,随着人类社会的工业化、现代化以及气候系统科学的不断发展,全球气候变化问题逐渐成为科学界和社会公众关注的焦点。近年来,许多学者对气候的变化趋势、突变性、周期性等特征进行了研究。王鹏祥等[4]分析了我国西北地区的降水量、气温和蒸发量的变化趋势及突变性;毕雪丽等[5]利用线性回归法、累积距平法、Mann-Kendall法,分析了河池市近56年来气候的变化特征;李琰等[6]采用1980—2006年陕西省榆林市12个县(区)的气温、降水资料,通过趋势分析、聚类分析对榆林市县域气候变化特征进行了研究。但对气候序列的均匀性及稳定性的研究相对较少。刘德地等[7]将云模型引入到降水量时空分布特征的研究中,对降水量在时间上分布的均匀性及稳定性进行了分析;赵璐等[8]采用云模型描述了潜在蒸发量的时空分布特征。本文拟运用云模型,分析四川盆地的年度及季度降水量、气温和蒸发量在时间上的分布特性;并运用Kendall秩次相关法,分析其在时空上的变化特征，以期为四川盆地气候变化研究提供科学依据。

1 数据和方法

1.1 研究区域

四川盆地是中国四大盆地之一,位于我国腹心地带和大西部东缘中段,囊括四川省中东部和重庆大部分地区。总面积约26万km2,周围山地海拔多在1 000～3 000 m,中间盆底地势低矮,海拔为200～750 m。四川盆地地形闭塞,气温高于同纬度其他地区,多年平均降水量1 000～1 300 mm。

1.2 数据来源

本文采用由中国气象科学数据共享服务网提供的1955—2010年四川盆地内15个气象站的月降水量和月气温资料,气象站站点位置如图1所示。研究区域内季节的划分方式为:3—5月为春季；6—8月为夏季；9—11月为秋季；12月至次年2月为冬季。

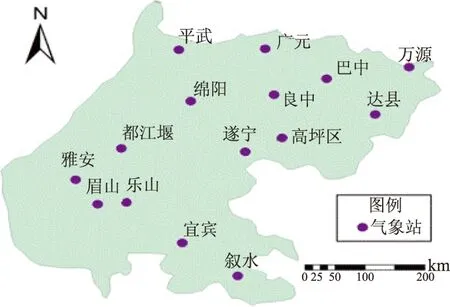
图1 气象站站点位置

1.3 分析方法

水文序列时空分布特征的研究方法有很多,常用的有线性倾向估计法、高桥浩一郎蒸发公式法、潜在非平稳气候序列趋势分析法、云模型、小波分析法、曼-肯德尔(Mann-Kendall)秩次相关法、基于GIS的空间插值分析法等。笔者选用高桥浩一郎蒸发公式法、云模型和Mann-Kendall秩次相关法对四川盆地气候变化时空分布特征进行分析。

1.3.1 高桥浩一郎蒸发公式法

高桥浩一郎蒸发公式是由高桥浩一郎推算出的经验公式,运用月平均气温、月降水量来推算月蒸发量[9]。

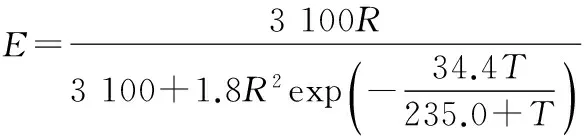
(1)

式中:E为月蒸发量,mm;R为月降水量,mm;T为月平均气温,℃。

高桥浩一郎蒸发公式虽为经验公式,但它在物理上考虑了影响实际蒸发的两个最主要物理因子(气温和降水量),并有实际观测资料做支撑,因此能较好地反映实际蒸发的变化情况[10]。

1.3.2 云模型

云模型作为处理定性概念与定量描述转换的不确定性模型,能够充分体现语言概念的随机性和模糊性,是实现定性与定量转换的有效工具[11]。云模型的数字特征用期望(Ex)、熵(En)和超熵(He)的数值来表示。

期望(Ex)为时间序列的平均值,是表示云滴在论域空间分布的期望, 是最能够代表定性概念的点,即概念在论域空间的中心值[11]。

熵(En)是定性概念不确定性的度量,是由定性概念的不确定性和模糊性共同决定的[11]；它也是定性概念随机性的度量,反映了能够代表这个定性概念的云滴的离散程度,即相对于平均值的离散程度,En值越大,表明序列越分散;它还是定性概念亦此亦彼的度量,反映了论域空间中可被概念接受的云滴取值范围。

超熵(He)是熵(En)的不确定性的度量,用来度量熵的不均匀程度,可称为熵的熵,由熵的不确定性和模糊性共同决定。He值越大,表明序列的熵越不稳定,He体现了序列不均匀性的稳定程度。

云的生成算法既可以用软件的方式实现,又可以用固化成硬件的方式实现,这种硬件称为云发生器(Cloud Generator)。云发生器分为正向云发生器和逆向云发生器。

1)正向云发生器。正向云发生器是最基本的云算法,它在表达自然语言中的基本语言值——语言原子时最为有用,实现了从语言值表达的定性信息中获得定量的范围和分布规律,是用来表征语言原子时最普遍、最重要的工具,是一个前向的、直接的过程。针对正态分布情况,若给定云的3个数字特征(Ex、En、He),可产生正态云模型的若干二维点——云滴drop(xi,μi),则称其为正向云发生器。

正向云发生器的算法过程主要为:输入数字特征(Ex、En、He),输出n个云滴xi及其确定度μi(i=1,2,…,n)。具体计算步骤如下[7]:

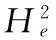
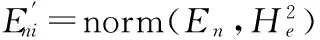
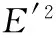
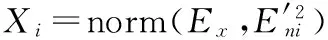
步骤3 计算云滴xi的确定度μi:

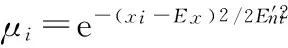
步骤4 生成具有确定度μi的xi，成为数域中的一个云滴。

步骤5 重复步骤1—4,直到产生要求的n个云滴为止。

2)逆向云发生器。给定符合某一正态云分布规律的一组云滴(Xi,Yi)作为样本,若产生描述云模型所对应的定性概念的3个数字特征(Ex、En、He),则称其为逆向云发生器。

逆向云发生器的算法过程主要为:输入样本点Xi，输出数字特征(Ex、En、He)。具体计算步骤如下[7]:

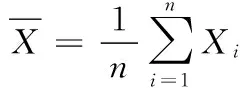
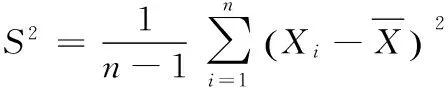
步骤2 计算样本数据的期望Ex、熵En及超熵He：

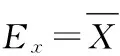
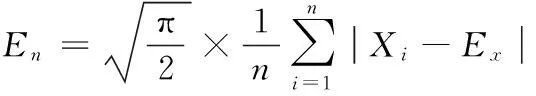
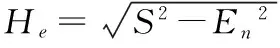
由步骤2可以看出,熵En和超熵He的大小与期望Ex相关。不同数据序列的熵和超熵相互对比时,若各序列的期望值相差较大,则不能准确地体现出各序列之间的相对离散程度及相对不均匀稳定程度的高低。因此,为了便于比较,将各序列分别除以各自的均值,使各序列的期望值均相同(都为1)。

1.3.3 曼-肯德尔(Mann-Kendall)秩次相关法

曼-肯德尔(Mann-Kendall)秩次相关法又可简称为Kendall秩次相关法，它是世界气象组织推荐并已广泛使用的非参数秩次检验方法。此方法计算简便，样本不需要遵从一定的分布规律,也不受少数异常值的干扰,适用于水文、气象等非正态分布的数据序列[8]。

x1,x2，…，xn表示样本容量为n的时间序列的变量,定义统计量s,可建立表达式[12]:

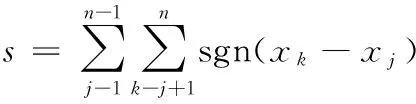
(2)

(3)

式中:xk、xj分别为k、j时间序列的序列值,k>j。

定义正态分布统计量Z[12]:

(4)

式中Var(s)为方差。

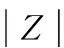
2 结果分析

2.1 云模型结果分析

利用云模型的逆向云发生器计算1955—2010年四川盆地的年度及季度降水量、气温、蒸发量的云模型数字特征,数字特征值见表1。

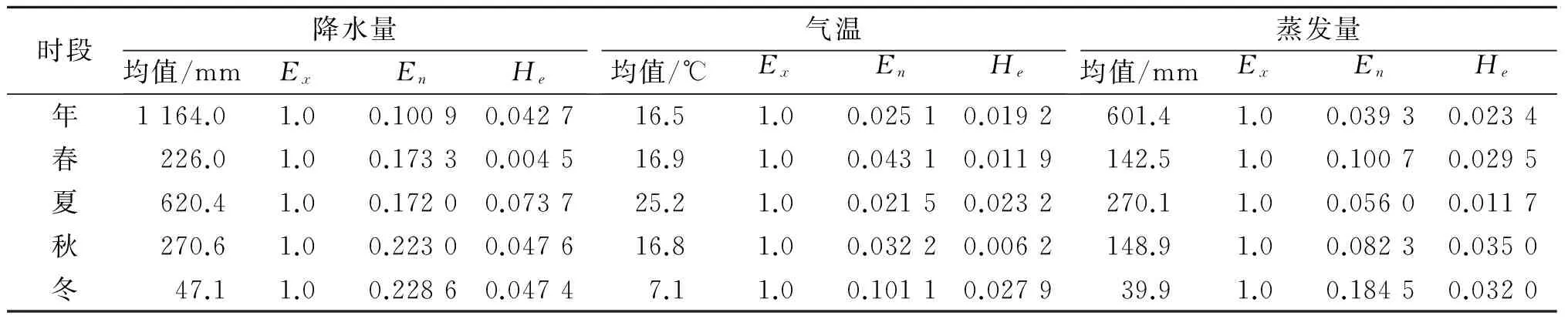
表1 1955—2010年四川盆地的年度及季度降水量、气温和蒸发量的云模型数字特征值

由表1可以看出:1955—2010年，四川盆地的多年平均降水量为1 164.0 mm,降水主要集中在夏季,夏季平均降水量占多年平均降水量的53.3%,冬季降水量最少,仅占多年平均降水量的4.0%;四川盆地的多年平均气温为16.5 ℃,春季和秋季的平均气温与多年平均气温接近,夏季平均气温最高,为25.2 ℃,冬季平均气温最低，为7.1 ℃;四川盆地的多年平均蒸发量为601.4 mm,占多年平均降水量的51.7%,4个季度中,夏季平均蒸发量最大,占多年平均蒸发量的44.9%。

利用云模型的正向云发生器计算1955—2010年四川盆地的年度及季度降水量、气温、蒸发量的云滴，并绘制相应的隶属云图,如图2所示。

由图2可以看出:

1)56年来,四川盆地的年度及度季降水量中(图2(a)、(d)、(g)、(j)、(m)),冬季平均降水量在时间上分布的离散程度即不均匀性最大,但其不均匀性相对较稳定;多年平均降水量在时间上分布最为均匀,但其不均匀性的稳定程度与冬季相差不大;夏季平均降水量的云滴分布最分散,说明其不均匀性的稳定程度较差;春季平均降水量的云滴分布明显较集中,说明其不均匀性的稳定程度较好。

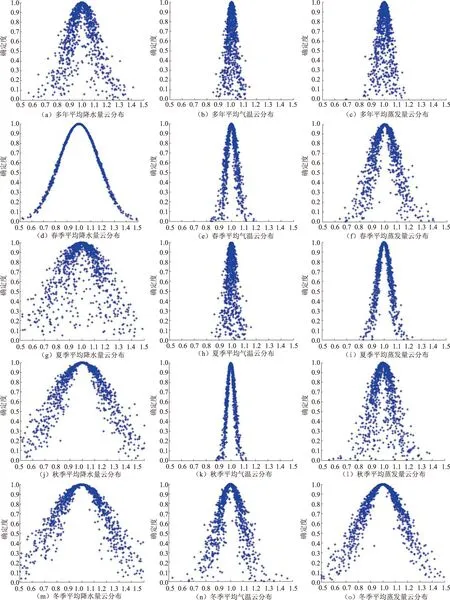
图2 1955—2010年四川盆地的年度及季度降水量、气温和蒸发量隶属云图

2)56年来,四川盆地的年度及季度气温中(图2(b)、(e)、(h)、(k)、(n)),夏季平均气温分布最均匀,但其稳定性相对不强;冬季平均气温分布最不均匀,且最不稳定;秋季平均气温分布相对较不均匀,但其稳定性最好。

3)56年来,四川盆地的年度及季度蒸发量中(图2(c)、(f)、(i)、(l)、(o)),多年平均蒸发量分布最均匀,且其稳定性较强;冬季平均蒸发量分布最不均匀,且其稳定性相对不强。

4)56年来,四川盆地的年度及季度降水量、气温和蒸发量序列中,气温序列在时间上分布最为均匀、稳定,其次为蒸发量,降水量序列的均匀性和稳定性相对较差。

2.2 四川盆地气候变化趋势分析

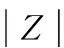
由表2可以看出,1955—2010年四川盆地的年度及季度降水量均呈减少趋势,但其减少趋势在99%置信区间内均不显著;年度及季度气温序列中,除夏季外，其余均呈上升趋势,且只有秋季的上升趋势在99%置信区间内显著;年度及季度蒸发量序列中,春季、夏季及冬季呈增加趋势,年度及秋季呈下降趋势，且所有变化趋势在99%置信区间内均不显著。

表2 1955—2010年四川盆地的年度及季度降水量、 气温和蒸发量的Z值统计表

利用基于GIS的反距离权重(Inverse Distance Weighted，IDW)法将趋势分析的Z值进行空间插值,结果如图3所示。

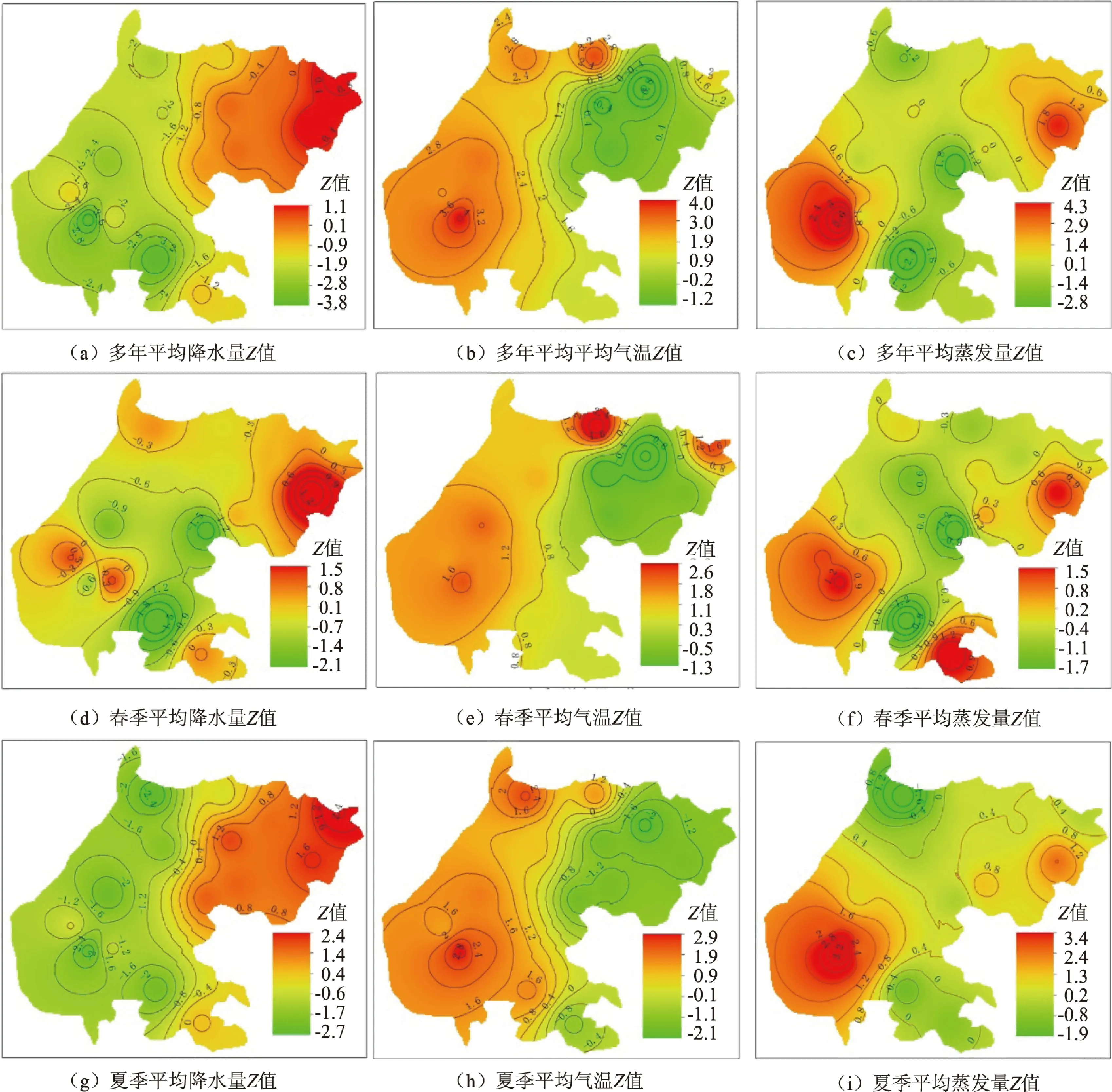
图3 1955—2010年四川盆地降水量、气温和蒸发量的Z值空间分布

由图3可知：

1)1955—2010年四川盆地的年度及季度降水量Z值均表现出东北部大、西南部小,且大部分地区Z值小于0,只有东北部小部分地区的Z值大于0,即四川盆地大部分地区的年度及季度降水量呈减少趋势。

2)年度及季度气温Z值的空间分布与降水量相反,大部分地区气温Z值大于0,只有东北部的少部分地区小于0,即四川盆地大部分地区的年度及季度气温呈上升趋势。

3)年度及季度蒸发量Z值空间分布中,除冬季外,其余均为东北部和西南部地区蒸发量Z值较大、中部地区较小;而冬季平均蒸发量Z值在东北部地区较大、西南部地区较小；年度及季度蒸发量Z值大都位于-2.58～2.58,即变化趋势在99%置信区间内不显著。

3 结语

通过对1955—2010年四川盆地内15个气象站的月降水量和月气温资料进行分析，得出的主要结论有：

1)降水量序列中，年内降水量主要集中在夏季,占多年平均降水量的53.3%。56年来,秋季和冬季平均降水量分布的均匀性和稳定性类似，但冬季的不均匀性最大,多年平均降水量分布的均匀性最好,春季平均降水量分布最稳定。

2)气温序列相对降水量和蒸发量序列，分布最为均匀和稳定。气温序列中,冬季平均气温分布均匀性相对较差,秋季平均气温稳定性最好。

3)蒸发量序列中,多年平均蒸发量分布最为均匀,稳定性也较好,秋、冬两季的稳定性类似,但冬季平均蒸发量分布的均匀性相对较差。

4)四川盆地绝大多数地区降水量呈减少趋势,气温呈增加趋势,东北部和西南部的蒸发量呈增加趋势,中部呈减少趋势。

5)由于收集资料以及文章篇幅的限制,本文仅对降水量、气温及蒸发量的分布特征及变化趋势进行了分析,未对其原因进行研究。下一步将继续收集、分析资料,对其原因做进一步的研究。

[1]任正果，张明军，王圣杰，等.1961—2011中国南方地区极端降水事件变化[J].地理学报，2014,69(5)：640-649.

[2]郑景云，郝志新，方修琦，等.中国过去2000年极端气候事件变化的若干特征[J].地理科学进展，2014,33(1)：3-12.

[3]王会军.气候变化研究与环境和发展问题紧密相扣[J].科学通报,2016,61(10):1027-1028.

[4]王鹏祥,杨金虎,张强,等.近半个世纪来中国西北地面气候变化基本特征[J].地球科学进展,2007,22(6):649-656.

[5]毕雪丽,张发旺,时坚,等.河池市近56年来气候变化特征[J].南水北调与水利科技,2016,14(2):105-110.

[6]李琰,刘晓琼,赵昕奕.陕西省榆林市气候变化特征分析[J].干旱区资源与环境,2011,25(1):157-161.

[7]刘德地,陈晓宏,楼章华.基于云模型的降雨时空分布特性分析[J].水利学报,2009,40(7):850-857.

[8]赵璐,崔宁博,梁川,等.基于云模型的四川省潜在蒸散量时空分布研究[J].四川大学学报(工程科学版),2013,45(1):91-97.

[9]周长艳,彭俊,李跃清.九寨沟、黄龙地区水资源的变化特征及成因分析[J].资源科学,2007,29(2):60-67.

[10]黄晓荣,奚圆圆,李晶晶,等.荥经河流域径流变化过程分析[J].华北水利水电大学学报(自然科学版), 2016,37(4):67-70.

[11]李健,汪明武,徐鹏,等.基于云模型的围岩稳定性分类[J].岩土工程学报,2014,36(1):83-87.

[12]霍正文,陈文,凡炳文.近54年定西市降水趋势及突变分析[J].水文,2012,32(3):88-92.

[13]YU Lanlan,XIA Ziqiang,LI Jingku,et al.Climate change characteristics of Amur River[J].Water Science and Engineering,2013,6(2):131-144.

(责任编辑：张陵)

Analysis on Characteristics of Temporal-spatial Climate Distribution in Sichuan Basin Based on Cloud Model

GAO Linyun1, HUANG Xiaorong1,2, XI Yuanyuan1, LI Jingjing1, MA Kai1

(1.College of Water Resource & Hydropower, Sichuan University, Chengdu 610065, China;2.State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China)

In order to study the temporal and spatial distribution characteristics of climate change in Sichuan Basin, based on the monthly precipitation and monthly air temperature data of 15 meteorological stations in the Sichuan Basin from 1955 to 2010, monthly evaporation was calculated using the Takahashi Koichiro evaporation equation. The cloud model is used to describe the distribution of precipitation, temperature and evaporation in time. The spatial and temporal distribution characteristics of precipitation, air temperature and evaporation were analyzed by Kendall rank correlation method.The results show that the distribution of precipitation is the most uneven in the annual and seasonal precipitation series from 1955 to 2010, followed by in autumn.In the annual and quarterly temperature series, the winter temperature distribution is the most uneven and the most unstable, but the autumn temperature distribution is the most stable.In the annual and quarter evaporation series, the distribution of evaporation in winter is the most uneven, and the annual evaporation is most evenly distributed. The annual and quarterly precipitation has been declining. In the annual and seasonal temperature, except the summer temperature, the others are on the ascending trend. The annual and autumn evapotranspiration showed a decreasing trend, and the evaporation in spring, summer and winter showed an increasing trend. The analysis of the spatial and temporal distribution of climate change in Sichuan Basin can provide scientific reference and technical support for climate change research in this region.

Sichuan Basin; climate distribution; cloud model; Kendall rank correlation method; precipitation; air temperature; evaporation

2016-10-28

国家自然科学基金面上项目(51579161);国家重点基础研究发展计划(2015CB452701)。

高蔺云(1993—),男,四川达州人,硕士研究生,从事水文水资源方面的研究。E-mail:glyun@foxmail.com。

黄晓荣(1972—),男,四川重庆人,教授,博士,从事水文水资源方面的研究。E-mail:hxiaorong@scu.edu.cn。

10.3969/j.issn.1002-5634.2017.01.001

TV211

A

1002-5634(2017)01-0001-07