以退为进:挑战新定义考题的有效策略
——北京海淀九上期末卷第29题解析与赏析
2017-03-11广西南宁市第二中学甘晓云
☉广西南宁市第二中学 甘晓云
以退为进:挑战新定义考题的有效策略
——北京海淀九上期末卷第29题解析与赏析
☉广西南宁市第二中学 甘晓云
近年来,有命题兴趣的同行都会关注和研究北京市各区的期末试卷,因为北京市各区的期末试卷往往都有很多原创的特色试题,这些试题贴近北京市中考题风格,很有数学味道,值得思考.本文赏析北京海淀区九上期末卷第29题,并跟进命题思考,供研讨.
一、考题解析与回顾反思
考题(2016~2017学年九上期末试卷,第29题)定义:点P为△ABC内部或边上的点,若满足△PAB、△PBC、△PAC中至少有一个三角形与△ABC相似(点P不与△ABC的顶点重合),则称点P为△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
在平面直角坐标系xOy中,
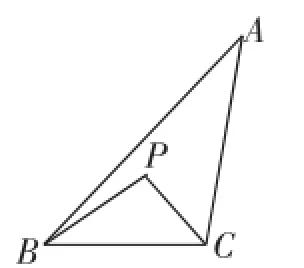
图1

图2

图3
②若k=2,点N的坐标为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有_____个,请在图3中画出这些点(保留必要的画图痕迹).
思路突破:
(1)只要构图连接OF、BF,结合F点的坐标,可确认∠OFB为90°,且∠FOB=30°,于是点F是△AOB的自相似点;再构图联系BG,会确认BG⊥AO,故G也是△AOB的自相似点.
(2)直接求解两问比较困难,找不到突破点,我们需要先深入思考新定义中的自相似点与三角形形状之间的关系.首先思考的是:自相似点P如果存在,那么△ABC的内角需要满足什么样的条件?我们可以从特殊三角形进行探究,得出如下结论:
第一,在△ABC的边上存在自相似点,当且仅当它的内角不全相等;
第二,在△ABC的内部存在自相似点,当且仅当它的内角都不相等.
进一步,我们可把三角形按边进行分类,研究自相似点的相关情况,如表1所示:

表1
有了上述准备工作,再思考考题第(2)问:
首先确定△OMN是等腰三角形(顶角为120°),则它的自相似点P一定在边上,可分析出如图4所示的草图贯通思路.
接下来给出详细思路:
①如图5,过点M作MH⊥x轴于H点.

图4

图5

图6
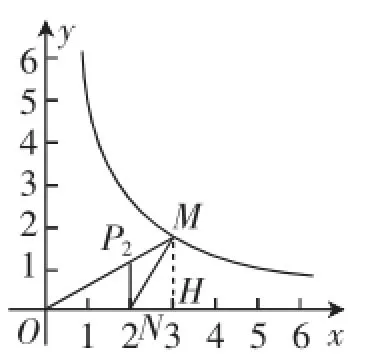
图7
如图6,△P1ON∽△NOM,过点P1作P1Q⊥x轴于Q点.
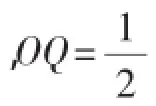

②首先想清△MON有两个自相似点,则它是等腰(非直角)三角形.这样问题的本质就是在曲线上确定点M,使△OMN是等腰三角形,可作出图8辅助分析,即分别以O、N为圆心,NO为半径作圆,与曲线有4个交点.注意:线段ON的垂直平分线与曲线的交点M5需要舍去,此时点M5(1,1)与O、N组成的△MON是等腰直角三角形,只有1个自相似点,这种情况应该舍去.
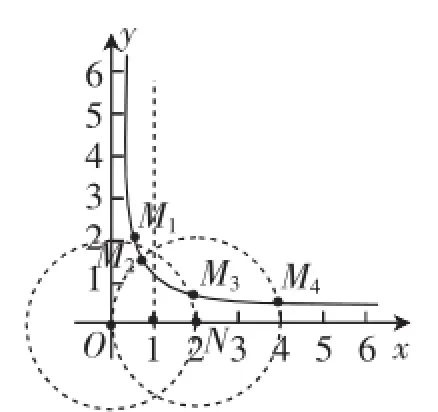
图8
反思回顾:这道考题最后两问比较抽象、晦涩,如果缺少对不同形状三角形的自相似点的深入分析,并总结出如上文中的表格特点,则探究曲线上自相似点就会无从下手,寻找解题切入点遇到障碍.特别是最后一问中ON的中垂线与曲线的交点需要舍弃,也需要想清楚.
二、“新定义考题”的进一步赏析
新定义考题在各地中考试题中出现已有不少年份,但是像北京市这样年年创新、年年不同,而且富有数学味、呈现简约、引发深思的新定义考题却不多见.不少低劣的新定义考题常常是把高中阶段一些概念或性质简单下放考查,使得考试的教学导向出现偏差,还有些地区的新定义考题出现理解晦涩甚至模糊不清的现象,不符合优秀试题追求简洁好懂、富于生长的特点.具体来说,北京海淀区这道新定义考题还可提出如下赏析.
1.新定义清楚好懂,举例说明助理解.
阅读新定义,需要理解自相似点只能出现在△ABC内部或边上,接着要辨别“何为自相似”,也就是解决新定义问题,要从解读定义开始.为了帮助学生理解新定义,命题组举例说明,并画出图形进行解读,这样有助于理解.这种命题思路在北京市近几年中考压轴题中都有体现,值得学习.
2.起步问题需构图,特殊图形助辨别.
考题的起步问题就将自相似点的确认放置在平面直角坐标系中进行研究,学生需要自主构造图形,并确认三角形ABO的特殊形状即真是一个含30°角的特殊直角三角形,并给出三个特殊点,标注出这些点之后,再发现这些点与其他边构成的直角三角形中是否会出现含30°角的直角三角形,从而确定只有两个点符合要求.这里从特殊出发解决问题的思路不仅对于这一道小题进行了处理,更重要的是要有“从特殊出发”“回到简单”的解题心理,因为后续问题还是需要更为全面地分析不同三角形自相似点的个数.
3.挑战考题有玄机,以退为进助突破.
考题的最后两问与前面新定义之间跳开较大的距离,要想顺利获得解题念头,则需要退回新定义,深入思考、全面分析不同形状相似三角形自相似点的个数,也就是上文中那张表格的分析,这需要消耗学生较多的时间,且短时间内还不一定能想准思考方向.所以面对这样的考题,在讲评时建议安排学生先探究直角三角形自相似点的个数,再过渡到等腰三角形、等边三角形自相似点的个数,待想清等腰三角形(非等边)自相似点个数之后,再挑战最后两问,则可以很快获得思路.这里需要让学生积累以退为进的解题策略.
1.吴忠妙.一道考题的思路、难点与教学设计[J].中学数学(下),2016(9).
2.郑毓信.多元表征与概念教学[J].小学数学教育,2011(10).
3.章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013(6).
