概化理论在中小学英语测试研究中的应用

王天剑

（贵州财经大学外国语学院 贵州贵阳 550004）

概化理论在中小学英语测试研究中的应用

王天剑

（贵州财经大学外国语学院 贵州贵阳 550004）

概化理论是将方差分析与传统的真分数理论整合发展而来的可靠度（信度）理论，它是现代教育和心理测量的重要理论之一。为帮助研究者掌握概化理论在中小学英语测试研究中的应用方法，文章讨论了概化分析中的基本概念，并以一套英语演讲能力评定程序可靠度研究为例，介绍了利用软件EduG进行概化分析的基本步骤。

概化理论；测试；研究

概化理论是关于行为测量可靠度的理论 (Shavelson& Webb,1991)[1](P1)。它是在经典测量理论（Classical TestTheory, CTT）与方差分析理论（ANOVA）基础上，经不同专家逐步发展而来的现代测量理论（Cronbach etal,1963[2](P137-163)；Cardinet etal,2010(pix)）。根据经典测量理论，观测分数（X）是真分数（T）与随机误差（E）之和（X=T+E）。真分数是对象某种特质的真实值，随机误差是测量过程中产生的所有偏差。哪些因素导致了随机误差？为回答这一问题，概化理论吸收了方差分析的思想，将随机误差进一步区分为不同来源的误差，估算各自所占比重，并计算可靠度系数（与经典测量的信度系数可以类比的参数），反应测量的精确度。使用概化理论，我们不仅可以评价既有测量程序的优劣，也可以探索测量优化的方案。正因其重要应用价值，概化理论在国外教育与心理测量中受到高度重视。美国教育研究协会、心理学协会和国家教育测量委员会联合提出的《教育和心理测量标准》(Standards for Education and PsychologyTesting，AERA,1999)明确提出，在建立观察和测量程序的信度与效度时，需参照概化理论（GeneralizabilityTheory,GT）[3](P34)。

学校的各种测验、测试、考试（本文统称“测试”）均属于教育或心理测量。近年来，国内已有学者开始利用概化理论理论研究英语测试。如，徐鹰等（2015）[4](P89-95)利用概化理论，分析了广东省高考英语听说模拟测试程序；孙海洋等（2011）[5](P61-65)对职前中学英语教师的口语测试进行了概化和多元化分析；张英莉等（2014）[6](P4-8)应用概化理论,对初中学生英语口试评分标准及评分者信度等进行了分析。这些研究披露了英语测试程序中存在的种种缺陷，对于优化测试方案具有重要参考价值。

测试贯穿中小学英语教学的始末。从安置性测试、平时测试、期末测试，到各种升学测试、竞赛测试等，无不需要具有较高信度和效度的测试程序。利用概化理论对有关数据进行分析，对于提高测试质量具有重要意义。鉴于国内关于概化理论应用的文献尚不多见，本文在介绍概化分析基本概念基础上，结合实例，简要描述利用工具软件EduG进行概化分析的方法。

一、概化分析的基本概念

（一）侧面。侧面是测量的对象以及构成测量条件的因素（相当于方差分析中的自变量）。例如，测试时间、测试地点、测试方式、测试题目、受试者（或其某种特征）、评分员（或其某种特征）等均可视为侧面，只要研究者对这些因素的影响感兴趣。诸因素中，测量对象被称作区别侧面，构成测量条件的因素被称作工具侧面。

（二）观察设计。在测量中，侧面之间就会形成不同的结构关系：

1.交叉关系，即每一个侧面的每个水平均与其他侧面的每个水平存在结合。例如，测试中涉及10个学生（S）和2个评分员（R）两个侧面，每个学生需要接受每个评分员评分，即S和R的各个水平均有接触，侧面之间构成交叉关系，表示为S×R，或者SR。其结果是，可以产生10×2=20个数据。

2.套嵌关系，即一个侧面的不同水平与且仅与另一个侧面的一个水平结合。例如，上述测试中，5个学生由评分员A评分，另外5个由评分员B评分，这时S的五个水平与R的一个水平接触，另外五个水平与R的另一水平接触，侧面之间构成套嵌关系，称作S套嵌于R，表示为S：R。其结果是，可以产生10个数据。

如果有三个或者三个以上的侧面作为测量条件，其间会形成更为复杂的关系。如对于A、B和C三个侧面，可以构成ABC(三个侧面完全交叉)，A:BC（BC交叉，A套嵌于BC），AB: C（AB为交叉，AB套嵌于C），或者A:B:C（A套嵌于B，而B进一步套嵌于C）等。

上述侧面之间的交叉或者套嵌关系，统称为观察设计，反映的是数据的结构关系。

（三）估计设计。估计设计需要回答的问题是：各个侧面是以多少个水平估计多大的全域（以多大的样本量估计多大的总体）？我们需要完成的操作任务是，确定测量涉及的每一个侧面分属于以下哪种类型：

1.固定侧面，即全域各个水平全部出现在研究中的侧面。自然的固定侧面很少，但研究者可以将一个侧面的某些水平人为地定义为全域，并将其全部容纳于研究中。例如，在一次测试中，某校将其仅有的5位高级英语教师作为一个评分员全域，并使其全部参加某次试卷的评阅，则评分员就是一个固定侧面（侧面水平=全域水平=5）。

2.有限随机侧面，即出现于研究中的水平是从有限全域中随机抽取的侧面。例如，某校将其仅有的5位高级英语教师作为一个评分员全域，某次试卷评阅中随机抽取2名作为评分员，则评分员就是一个有限随机侧面（侧面水平=2，全域水平=5）。

3.无限随机侧面，即出现于研究中的水平是从被视为无限大的全域中随机抽取的侧面。例如，英语教师可被视为一个无限大的全域，某次试卷评阅中随机抽取5名作为评分员，则评分员就是一个无限随机侧面（侧面水平=5，全域水平=Infinite）。

基于不同的抽样方式获得的研究结果，在适用范围（概化）方面不同。例如，当评分员是一个固定侧面时，研究结果在概化时，仅适用于同样的评分员参与的测量；当评分员是随机侧面时，结果可以概化到随机抽样的全域中。侧面的随机性或固定性随研究目的而定，研究者可以根据研究兴趣进行双向修改（将固定侧面更改为随机侧面，或将随机侧面更改为固定侧面）。一个研究程序中可以同时容纳固定侧面与随机侧面（这样的模型叫做混合模型）。

（四）测量设计。测量设计部分的任务是：确定哪些侧面是区别侧面，哪些是工具侧面；确定测量是相对的，还是绝对的。

1.确定区别侧面与工具侧面。区别侧面是研究的焦点或者研究对象。工具侧面是完成测量需要依赖的各种条件因素。在教育研究中，一般情况下学生是区别侧面，因为我们倾向于关注学生的成绩数据是否可靠。其他因素大多视为工具侧面，它们是为测量学生服务的。但是我们可以将区别侧面和工具侧面换位使用。例如，在一个由学生（S）、试题（T）和评分者（R）组成的交叉设计（STR）中，如果旨在考查学生的得分是否可靠，则学生为区别侧面，其他因素为工具侧面（表示为S/TR）；如果旨在检查不同试题项目得分高低的稳定性，则试题变成区别侧面，学生和评分员变成工具侧面（T/SR）；如果旨在检查不同评分员给分差别的稳定性，则评分员为区别侧面，学生和试题变成工具侧面（R/ST）。

2.确定测量是相对的还是绝对的。为了将个人（或研究目标）排名进行的测量叫做相对测量。例如竞赛、拔尖、择优之类的测试均为相对测量，因为我们的目的是比较高低，鉴别优差。为了了解个人（或研究目标）分数水平的测量叫做绝对测量。例如，目标测试、掌握性测试、学期测试、过级测试、毕业测试一般均作为绝对测量，因为我们倾向于关注个人成绩是否达到某一合格线。绝对测量是一种更加精确的测量，不仅能区别名次，而且能鉴定个人分值是否达到合格线。概化分析中，相对测量和绝对测量的可靠度是依据不同的参数衡量的。

二、概化研究举例

借助软件进行概化研究非常简便。现以一套英语演讲能力评定程序的导航研究为例，展示利用EduG进行概化分析的方法。

（一）问题描述。为了确定一套英语演讲能力评定程序的可靠度，某学校进行了一个导航研究：随机抽取10名初三学生作为被试，2名英语教师为评委，要求评委从语音、语法、词汇、内容四方面（能力维度），对被试的演讲进行评价。每个维度均需在一个三级量表上打分：“差”记1分，“中”记2分，“优”记3分。由于两个评分员都要对四个维度进行打分，每个被试可以产生8个原始分数，最后需要以8个分数的平均值作为每个被试的综合成绩，并根据综合成绩将所有被试排名。表1是某个被试的得分样例：

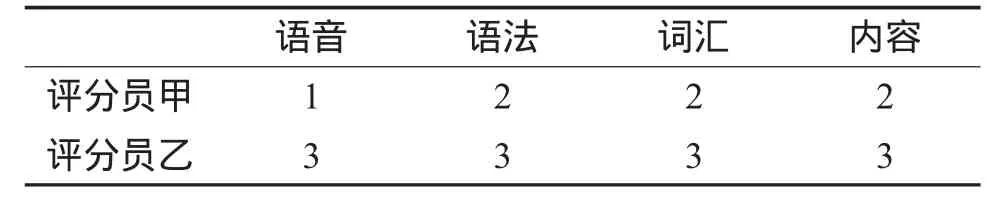
表1 被试不同能力维度得分样例（平均2.375）

10名被试在各维度上的原始分数共计80个。试根据这些数据，利用概化理论分析该评分程序的可靠度。

（二）问题分析。

1.观察设计。本例共有三个侧面：学生（10个水平），评分员（2个水平），能力维度（4个水平）。因每个评分员均要对每个学生在每个维度上评分，三个侧面的各个水平均有接触，所以这是一个完全交叉设计：学生（S）评分员（R）能力维度（Q），或者SRQ。

2.估计设计。本例的被试学生和评分员是通过随机程序抽取的，其全域可视为无限，这两个侧面均为为无限随机侧面。能力维度不是随机抽取的，而是特意确定的，所以为固定侧面，其全域水平为4。

3.测量设计。本例着重考查评定程序对学生演讲能力测量的可靠性，因此学生是区别侧面（即研究对象），评分员和能力维度则构成工具侧面（测评的条件因素），这种关系可以表示为S/QR。由于演讲比赛评分的目的是排名，测量是相对的。

（三）输入程序指令。为了利用EduG软件进行概化分析，需打开软件，并在界面中按如下方式填写指令（见图1）。

图1 概化分析指令界面

完成如上指令的具体步骤包括：

1.确定文件名称与保存位置。运行软件，依次点击File 和New，在弹出的界面中填写文件的存储名称和位置（本例名称取“example1”，保存位置为F盘）。

2.打开文件，在界面中填写相关指令。

●在Title后填写文件的标题（这是分析报告中使用的标题，本例用Procedureforrankingspeakingability）；

●在Numberoffacets后选3，表示分析涉及三个侧面；

●在Observation and estimation designs之下填写各侧面的英文名称（Student,Rater,Quality），名称的字母代码（S,R,Q，代表三个侧面处于完全交叉关系）。填写各侧面的水平（10,2, 4），各侧面的全域容量（本例中学生和评分员来自无限全域，表示为INF；能力维度全域水平为4）；

●在Measurementdesign后填写测量设计代码（S/RQ，表示学生是区别侧面，评分员和能力维度是构成测评条件的工具侧面）；

●在Reports下勾选RTF（表示输出的结果以Word表格形式呈现）；

●其他选项保持默认值。

●插入数据。点击Insertdata，选择scores，即弹出数据录入界面（见图2）。第一列表示的是学生序号，第二列是评分员序号，第三列是能力维度序号。前三列是软件根据观察设计自动生成的，第四列是需要我们录入数据的位置。一个学生要受两个评分员在四个维度评价，故有8个原始数据，10个被试的原始数据共计80个，可以依次录入表中。

图2 数据录入界面

（四）查看结果。录入如上程序指令和数据后，点击Compute，即可查看结果，主要包括如下部分。

1.哪些因素对学生的分数变化有较大影响？

表2 方差分析表

表2是输出的方差分析结果。各列依次表示对被试得分具有潜在影响的因素（侧面及其交互）、平方和、自由度、均方、随机效果模型方差成分、混合效果模型方差成分、Whimbey’s矫正的方差成分、各矫正成分的百分比及各随机效果模型方差成分的标准误。跟据表2第一列和第八列可知，有三个因素对被试得分影响分量较重：

SRQ（学生、评分员和能力维度的交互作用）：51.7%

SR（学生和评分员的交互作用）：28.8%

S（学生）：16.1%

交互作用意味着，两个评分员对不同学生的打分（SQ交互作用），以及两个评分员对不同学生在不同能力维度上的打分（SQR交互作用）分歧较大。学生作为研究目标，对分数的影响仅有16.1%，没有的达到足够的分量。

2.研究结果是否可靠？在概化中，测量误差源于那些侧面？表3呈现的是概化研究表（G-StudyTable）。其中第一列是研究对象，即区别侧面（本例是指学生），第二列是区别侧面的方差（相当于经典测量中真分数解释的变异，这里可理解为“学生的能力可以解释的得分变异”），第三列是潜在的误差来源（注意：由于能力维度Q为固定侧面，不存在随机抽样误差，故该侧面及其交互作用对测量误差的影响为零），第四、五列为相对误差方差及其百分比，第六、七列为绝对误差方差及其百分比。各列数据是进一步计算可靠度系数的依据。

由于本例属于相对测量，需要根据相对概化系数（Coef_Grelative），以及相对误差方差判断测量的可靠度与误差根源。Coef_Grelative=0.53＜0.80，即相对概化系数没有达到0.80这一惯用的临界值，表明测量可靠度不够理想。这里的0.53也意味着，在概化中，“真分数”能够解释的变异占53%，误差能够解释的变异占47%。哪些因素导致了概化中的测量误差？是SR，虽然其方差为0.07569，但因它是唯一的误差源，故解释全部误差（100%）。

表3 概化研究表

（五）优化设计方案。概化研究的特殊价值在于，它不仅能发现问题，而且能提供解决问题的方案。如何提高研究结果的可靠度？一般而言，可以通过增加随机工具侧面的抽样水平，或者剔除固定工具侧面中的不适宜水平，来达到提高测量结果可靠度的目的。

1.剔除固定工具侧面中的不适宜水平。剔除固定工具侧面中之不适宜水平的理论依据是，固定工具侧面中的某些水平缺乏效度，会增加测量误差。本例中能力（Q）为固定工具侧面，其四个水平依次为语音、语法、词汇和内容。利用EduG中的G-Facetsanalysis，便可探明本侧面哪一水平删除后能够提升相对概化系数。步骤为：

（1）勾选G-Facetsanalysis（G侧面分析）；

（2）在弹出对话框内勾选Q并点击OK;

（3）点击Compute并观察输出结果。

表4G侧面分析结果

表4呈现的是G侧面分析结果。表中第三栏是删除能力侧面某一水平后相对概化系数（Coef_Grel.）可以达到的新高度。显而易见，删除水平二（Level2,即语法），可以将相对概化系数最大幅度提高（达到0.68725）。可以推论，语法作为一个评定维度，会增加学生与评分员的交互作用（SR），扩大测量误差。删除语法项将有助于优化测量程序，提高结果的可靠度。

2.增加随机工具侧面的抽样水平。凡是以样本代表总体的研究，样本量越大结果越准确。这是通过增加随机工具侧面之抽样水平，以提高测量结果的原理。本例评分员（R）为随机工具侧面，借助EduG可以探明，如何在可操作的范围内适当增加其水平以获得可靠测量结果。由于剔除能力维度之水平二（语法），可以提高结果可靠度，在增加评分员时可以将剔除能力维度水平二作为并列条件。分析步骤如下：

（1）指定剔除能力维度二为并行条件（在Observationand estimationdesigns中Quality一行最后一个方框内点击，在弹出对话框内选2，点击OK。结果见图3）；

图3 剔除能力维度二后的观测与估计设计界面

（2）改变评分员抽样水平数（勾选Optimization，在弹出对话框中输入如图4的内容，注意在五中优化方案中，将R的观察水平依次更改为3,4,5,6,7，点击OK）;

图4 优化方案界面

(3)点击Compute观察输出结果。表5是输出的优化方案。表中显示了不同优化方案下的结果（绝对概化系数、误差方差、测量标准误等冗余数据略去）。根据相对概化系数的变化可知，评分员越多，系数越高。要达到可接受水平（系数大于或等于0.80）[7](P117-123)，至少需要4位评分员（即Option2，相对信度为0.81464）。

表5 优化方案分析表

总之，剔除一个评分维度（语法），额外增加两个评分员（达到4个），便可预期测量程序达到可靠评价学生能力的目的。但是，也有一个前提条件，在测量程序的实际推广应用中，随机抽取的评分员或者受试学生，必须与导航研究中涉及的人员具有类似性。否则，导航研究结果便失去推广的基础。

三、结语

概化理论是将方差分析与传统的真分数理论整合发展而来的信度理论。借助概化研究分析，我们不仅能够了解不同因素对测量结果和测量准确度的影响，评价测量程序的信度，判断结果的可靠度，也可以找到测量程序的优化方案，进而获得满意的结果。本研究借助具体案例，介绍了概化分析软件EduG的使用方法。由于篇幅有限，只能展示部分基本用法，希望对中小学英语教育测量有益。

[1]ShavelsonRJ,WebbNM.Generalizabilitytheory:Aprimer [M].SagePublications,1991.

[2]Cronbach.L.J,Rajaratnam,N,&Gleser,GC.Theory of generalizability:A liberalization of reliability theory[J].British JournalofMathematicalandStatisticalPsychology,1963(2).

[3]AmericanEducationResearchAssociation(AERA),American Psychological Association (APA),National Council on MeasurementinEducation(NCME).StandardsforEducationand PsychologyTesting[M].WashingtonDC:AmericanPsychological Association,1999.

[4]徐鹰，曾用强.基于概化理论和多层面Rasch模型的计算机化英语听说考试评分研究[J].电化教育研究,2015(3).

[5]孙海洋，韩宝成.概化理论在口语考试设计中的应用研究[J].外语教学，2011(11).

[6]张英莉，姚春艳.初中英语口语测试信度的概化理论应用研究[J].教育测量与评价(理论版),2014（2）.

[7]靳雪莲，滕金生，杨德山.网络论坛公共事务讨论语言的修辞特征和成因[J].重庆邮电大学学报(社会科学版)，2014（5）.

[责任编辑 刘金荣]

H319

A

2095-0438（2017）02-0119-05

2015-10-15

王天剑（1968-），河南南阳人，贵州财经大学教授，博士，硕士生导师，研究方向：应用语言学。

贵州省科学技术厅贵州财经大学软科学研究联合基金资助项目（黔科合LH字[2014]7262）。