切换非线性系统全局优化运行的经济预测控制
2017-03-10杨亚茹李少远
杨亚茹 李少远
化工生产过程中对于生产运作的需求,已从过去着重考虑系统的稳定性,转变至兼顾系统安全稳定下同时优化全局系统运行的经济性.这里的经济性通常用一类定义在系统工作范围的经济指标(泛指一类评价系统运行状况的性能函数)评价,全局优化运行的目标,是使得系统实际闭环运行轨迹在允许的工作范围内,同时尽可能减少各时刻工作状态对应的经济指标在整个生产过程的累积量.大型系统的全局优化常用分层递阶控制结构将生产中对于安全、鲁棒、经济等多目标逐层分解.实时优化层根据调度层的计划与排产信息,从面向全局系统整体经济性的角度,给出满足各子系统运行约束的稳态经济优化点.下层先进控制层常用MPC(Model predictive control)动态跟踪上层给出的稳态经济优化点,综合处理系统运行过程中的约束与扰动,并给底层各控制回路合适的设定值.同时,新工业需求下的全局优化运行还要求系统在工作过程中,对定制生产下不同排产计划、更小尺度的对象模型变化(如不同批次组分差异的原料、不同反应过程工况变化)都有对应的系统模式变化,在这种情况下的全局优化问题可归结于讨论切换非线性系统在双层控制结构下的经济优化运行.
目前多数非线性系统全局优化运行的运作模式是建立在“稳态假设”[1]基础上,因此,非线性系统模式切换的研究热点在于保证各个模式运行工作点的稳定性、鲁棒性及模式间的平稳过渡[2−6].其中,由于控制时域受到计算负担限制,不同模式下优化问题的可行域未必存在交集,有一部分研究工作考虑限制计算量的情况下保证系统在大工作范围内切换可行性[7].新工业需求下,系统频繁的切换使得“稳态假设”不能满足,运行动态过程中的经济性变的不可忽略.近年来,学者将经济预测控制[8−10](Economic model predictive control,EMPC)运用到切换非线性系统中,对于提高系统在整个运行过程中的经济性有显著贡献.EMPC是一种在形式上、运行策略上与实时求解的MPC相同的滚动时域控制算法,其在每一时刻同样需实时求解一个有限时域最优控制问题.但EMPC的控制性能指标为直接与经济指标相关的广义性能指标,正定性和(或)凸性不再保证.因此,在讨论稳定性问题上,EMPC常常需要引入额外的假设条件或约束.常规的方法主要有以下两种:文献[8]中首次提出的耗散性条件通过构造关于经济性能指标、系统模型、稳态经济优化点的不等式约束关系,构造了对应的Lyapunov函数,从而保证稳态经济优化点的稳定性.以此假设为基础,后续工作拓展至终端集约束EMPC[9]、无终端约束EMPC等[10];另一类方法通过构造辅助Lyapunov函数和(或)Lyapunov控制器,将其作为约束放入控制率实时求解的问题中,针对连续系统有文献[11−12],离散系统有文献[13−14].该类方法在一定程度上增大算法吸引域,但闭环系统的经济性能将受限于所构造的辅助控制器及辅助Lyapunov函数.
针对非线性切换系统的EMPC,目前的工作在系统前后模式可行域存在交集的前提下,保证了切换过程的平稳过渡并提高了经济性能[12,15].文献[12]采用基于Lyapunov函数的EMPC,每个模式下EMPC的吸引域为辅助控制器的可控集,前后两个模式算法吸引域需存在交集;文献[15]基于拓展时域终端集约束EMPC[16]的方式保证稳定性,其前一模式下的稳态优化点需位于后一模式终端约束集中.受限于EMPC讨论稳定性的复杂性,对于在大工作范围内的切换系统,如何考虑过渡过程的经济性能并平稳切换,还未有成熟的工作.
针对这一问题,本文采取的思想是构造一系列可行中间过渡稳态点拓展前后模式的可行域,通过设计局部EMPC控制器,将状态逐次转移至中间点并完成切换.在这一策略下,本文构造了基于耗散的EMPC辅助性能指标,在辅助性能指标控制下的EMPC能够保证任一可行稳态点渐近稳定,并尽可能逼近原经济性能指标;进一步,本文设计了对应的切换策略,在模式常规运行时,算法保证状态稳定在该模式的稳态经济优化点.同时,在模式切换时根据前后模式的经济指标求解和更新可行中间点及最优轨迹,将状态逐次转移至中间稳态点并利用最优轨迹保证状态在模式间的平稳过渡.所提方法适用于存在不可达问题的非线性切换系统,实际可操作性强,在保证平稳切换的基础上提高了暂态过程的经济性,仿真结果验证了算法的有效性.
符号说明:集合I表示非负整数集.S≥a表示集合满足S≥a={x∈S;x≥a},同样,S[a,b]={x∈S;a≤x≤b},其中a,b∈I.|·|表示欧几里得范数.Bxs(r)表示闭球域满足:ClassL表示一类定义在γ:上的连续且单调递减函数,满足limx→∞γ(x)=0,f◦g(x)表示复合函数f(g(x)).
1 问题描述及基本定义
考虑如下非线性系统离散时间模型:

假设 1.经济性能指标上连续,且各模式下模型fi(·) 在Xi×Ui上利普希茨连续,满足:
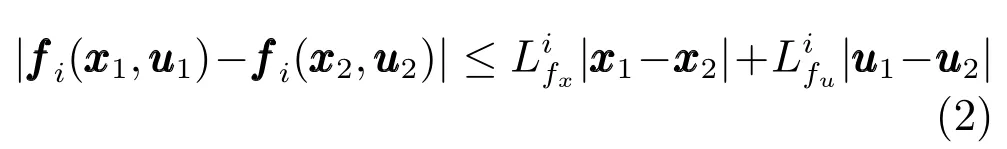
假设 2.模式i下存在(但不唯一)稳态经济优化点为如下问题的最优解,不失一般性,

定义1.模式i下的稳态点的N步可达状态集合为

定义2.N步可控至的初始可行状态集合为
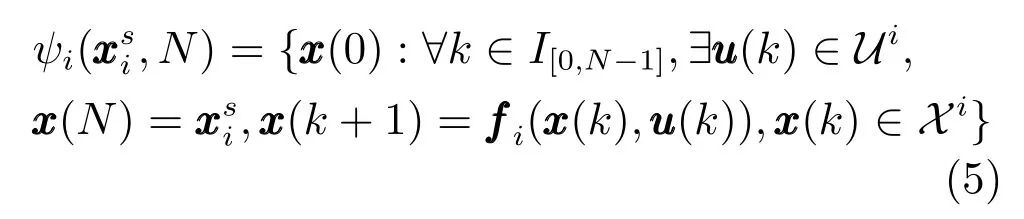
定义3.模式i下,控制时域为N时与稳态点相关的成对可行约束集定义为

假设3.模式i下对应的成对可行约束集均满足且为紧集.
类似于多数EMPC文献[8−12]中关于系统实际运行经济性的定义,对于每一模式确定的本文所考虑的切换系统暂态过程经济性(Transient performance)为下述形式:

本文的目的是设计针对非线性切换系统全局优化运行的EMPC算法,保证i模式常规运行时系统稳定在指定的稳态目标优化点模式间切换时保证系统平稳切换至新模式并提高暂态过程的经济性,本文并不要求相邻模式间常规运行时EMPC算法吸引域存在交集,仅要求在状态约束和输入约束范围内存在有限个控制时域可达集或可控集相交的中间稳态点,满足如下假设.
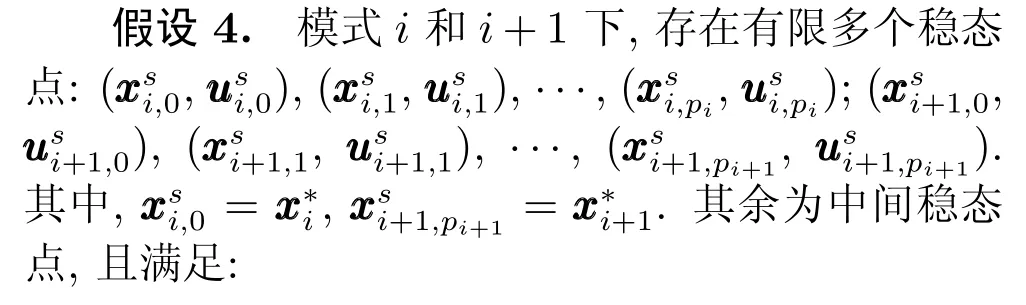

或可表述为

注1.假设4包括的情况,大多数非特殊性连续化工切换系统在采样时间足够短的情况下,其离散表述均能满足假设.
2 基于耗散性条件的全局优化运行EMPC
对于具有稳态运行需求的化工过程,需保证任一模式下的系统渐近稳定在稳态优化点切换过程中,由于控制时域N受计算负担限制,新模式的稳态点对于旧模式当前状态常常是控制时域内不可达的,即且本文采取的策略如图1所示,首先,该切换算法优化求解可行中间稳态点使其满足条件(8)和(9).其次,将状态依次经济转移至中间稳态点最终进入中.由于EMPC在保证稳定性上更具复杂性,问题的难点在于局部EMPC算法如何使状态偏离该模式下的稳态优化点,并渐近稳定至中间稳态点,并在有限时间Tp内完成经济切换.

图1 模式间切换策略Fig.1 Modes switching strategy
为后文阐述方便,本文将先进控制层EMPC需动态实时求解的如下非线性约束优化问题表述为

注2.不同于MPC,性能指标l非凸非正定.
首先介绍EMPC中与稳定性相关的重要定义与引理.

通过耗散性条件,将经济性能指标转化为正定的旋转性能指标,并附加终端等式约束保证递推可行性,同时旋转性能指标控制下的控制问题与原问题同解,与旋转性能指标相关的李雅普诺夫函数保证稳态优化点的渐近稳定.本文接下来的内容,将先提出一种保证任一可行稳态点渐近稳定的EMPC算法,再阐述与该算法对应的系统模式间切换策略.
2.1 适用于非稳态目标优化点的EMPC

注4.给定满足定理1假设条件的正定连续函数,如已经设计好的MPC性能指标,可通过条件(13) 确定进而找到
注5.由定理1知,可以理解为给系统提供耗散性质的函数.



由定理3的证明过程,可得上界¯δ.考虑到实际应用时可操作性,可由下述约束优化问题的优化函数最优值替代满足

2.2 非线性切换系统的经济预测控制
考虑实际化工生产系统工作特点,默认当系统接到切换至i+1模式的切换请求时已稳定工作在工作步骤如下:

步骤 2.首次迭代时,系统接到切换请求,并根据下一模式信息确定中间稳态点的个数pi,pi+1,进入步骤 2.1;否则,若pi̸=1且pi+1̸=0,则进入步骤2.2;若pi=1,pi+1=0,则目标点设置为上次迭代备用稳态点进入步骤3.

步骤2.1.置pi=1,pi+1=0.此时当前状态参考文献 [19]求解从稳态点之间是否存在可行轨迹.其中,np=pi+pi+1,κ1=pi(N+1),κ2=(np+1)(N+1)−1.若无解,依次增大pi,pi+1:pi=1,pi+1=1,pi=2,pi+1=1···,直到中间点问题(23)存在可行解.

步骤4.更新pi,pi+1.若pi>0,则pi=pi−1,pi+1=pi+1;否则,pi=pi,pi+1=pi+1−1.


注9.中间点问题及辅助性能指标的构造具有较大的计算量,在RTO层中求解.该切换算法要求准备时间Tp应至少满足Tp≥N×pi.因此,若准备时间非常短时,可以考虑改变步骤2.1中初始求解中间点个数时的策略.
注 10.若m̸=m′,表示实际系统即将发生切换.Tp足够长时,实际切换信号由状态决定,系统状态到达时发生切换;Tp受限时,切换信号由时间决定,实际切换时刻即为τi+Tp.因此,

注 11.由于辅助序列(24)为满足动态模型的状态与输入轨迹,因此问题(25)每一时刻都满足递推可行性,在约束集内均有可行解.
注12.在第一次运算确定好pi,pi+1后,步骤2每次迭代均有可行解,这是由于k=K+N+1时,由上一时刻问题(25)的最优解可构造从当前状态到目标点的可行轨迹,同时与上次迭代步骤2获得的从的最优轨迹,共同构成步骤2的初始可行解.
3 切换过程暂态经济性分析

对于终端等式约束,旋转性能指标与原性能指标求解优化问题下的优化轨迹完全相同,且优化问题最优值只相差个常数项.因此:

求和号表示上式中对应向量在[0,Ts]时刻的累加,为与参数δ,函数αi,及切换时间TS,暂态过程时间τi+1−τi相关的误差项.是求取中间点问题的最优函数值.
2)切换时间受限,此时TS=Tp=K+N,K时刻状态位于中间点邻域:

考虑k∈[K,K+N):此时实时求解经济切换问题(25).K时刻,该问题与有相同最优解与最优轨迹且最优值满足关系:

后同可得式(34)和(35).
经过分析,当准备时间受限时,采用步骤5的策略利用中间点问题得到的最优轨迹构造切换问题终端动态轨迹,暂态性能上与准备时间充足的情况有相类似的上界,该上界与中间点问题的最优值、所选耗散函数α、差值函数γ、暂态过程时间有关.
4 仿真验证
考虑连续搅拌釜(Continuous stirred tank reactor,CSTR)系统[9],其中发生不可逆反应A→B,副反应B→C.具体描述如下:
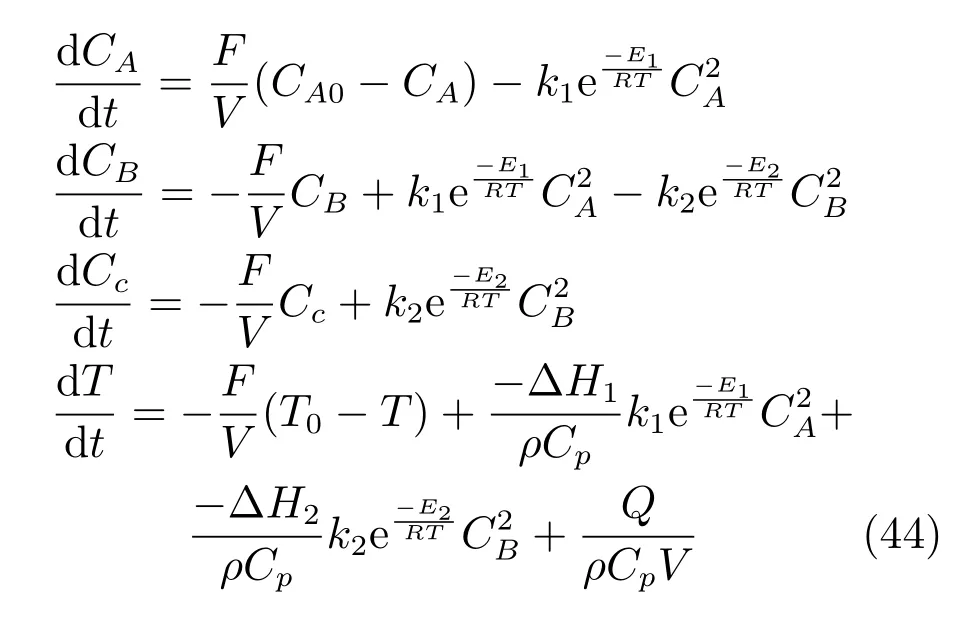
其中,CA,CB,Cc表示产物中反应物A,产物B,C的浓度;T表示反应器温度,Q表示提供给反应器的热量,为可控变量;反应器的体积为V=1m3,与反应相关参数为:E1=5000kJ/kmol,E2=4000kJ/kmol,k1=176.94h−1,k2=10.88h−1,∆H2=1.05×104kJ/kmol,∆H1=1.15×104kJ/kmol.Cp=0.231kJ/kgK和ρ=1000kg/m3为反应器中液体的比热容和密度,除此之外,常数R和F分别为8.314kJ/kmol,5m3/h.



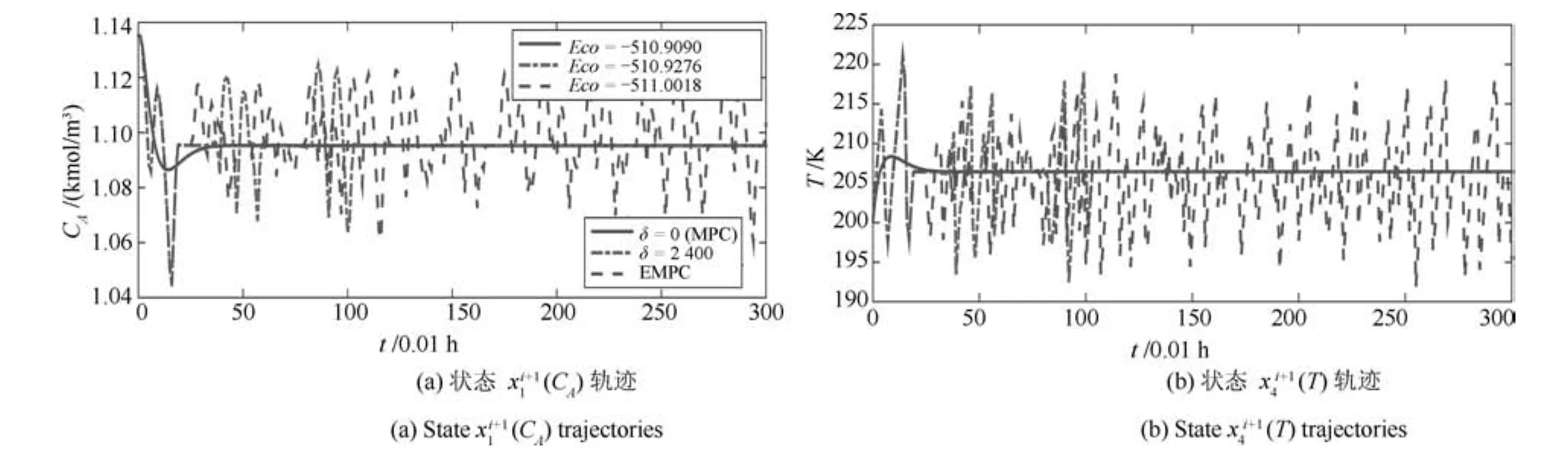
图2 在不同控制器下的稳定性Fig.2 Stability ofunder different controller

图3 在不同控制器下的稳定性Fig.3 Stability ofunder different controller

图4 采用NMPC及所提策略控制下的切换轨迹Fig.4 Comparing between proposed method and NMPC
采用本文第2.2节的切换策略实现切换,如图4所示,t=75时系统接到切换请求,切换时间受限,t=130时系统进入式(25)的过渡过程,t=150时系统发生切换,并将状态拉至新稳态点.系统3个小时内实际经济性能(每一时刻累加):MPC:Eco= −483.5873,所提方法:Eco= −484.9821.因此,式(7)所定义的切换系统暂态过程经济为所提方法较非线性MPC提高了43.17%.
5 结语
本文考虑了系统全局优化运行时所涉及的模式间不断切换对于经济性的需求,针对不同模式有限时域下控制算法可行域未必存在交集的系统,基于耗散性条件设计了一种保证可行稳态点渐近稳定的EMPC及对应切换策略.该方法通过优化求解可行中间稳态点,并设计一系列EMPC局部控制器,在保证了中间点的稳定性的基础上使系统在模式间平稳切换,暂态性能尽可能逼近原EMPC性能,可操作性强.仿真结果说明了方法的有效性.
1 Flemming T,Bartl M,Li P.Set-point optimization for closed-loop control systems under uncertainty.Industrial&Engineering Chemistry Research,2007,46(14):4930−4942
2 Liberzon D,Morse A S.Basic problems in stability and design of switched systems.IEEE Control Systems,1999,19(5):59−70
3 Hespanha J P,Morse A S.Stability of switched systems with average dwell-time.In:Proceedings of the 38th IEEE Conference on Decision and Control.Phoenix,AZ,USA:IEEE,1999,3:2655−2660
4 Li Shao-Yuan,Xi Yu-Geng.Switching smoothly of multimodel predictive control systems.Journal of Shanghai Jiaotong University,1999,33(11):1345−1347(李少远,席裕庚.多模型预测控制的平滑切换.上海交通大学学报,1999,33(11):1345−1347)
5 Lin Xiang-Ze,Li Shi-Hua,Zou Yun.Output feedback stabilization of invariant sets for nonlinear switched systems.Acta Automatica Sinica,2008,34(7):784−791(林相泽,李世华,邹云.非线性切换系统不变集的输出反馈镇定.自动化学报,2008,34(7):784−791)
6 Chai Tian-You,Zhang Ya-Jun.Nonlinear adaptive switching control method based on unmodeled dynamics compensation.Acta Automatica Sinica,2011,37(7):773−786(柴天佑,张亚军.基于未建模动态补偿的非线性自适应切换控制方法.自动化学报,2011,37(7):773−786)
7 Wan Z Y,Kothare M V.Efficient scheduled stabilizing output feedback model predictive control for constrained nonlinear systems.IEEE Transactions on Automatic Control,2004,49(7):1172−1177
8 Diehl M,Amrit R,Rawlings J B.A Lyapunov function for economic optimizing model predictive control.IEEE Transactions on Automatic Control,2011,56(3):703−707
9 Amrit R,Rawlings J B,Angeli D.Economic optimization using model predictive control with a terminal cost.Annual Reviews in Control,2011,35(2):178−186
11 Heidarinejad M,Liu J F,Christo fides P D.Economic model predictive control of nonlinear process systems using Lyapunov techniques.AIChE Journal,2012,58(3):855−870
12 Heidarinejad M,Liu J F,Christo fides P D.Economic model predictive control of switched nonlinear systems.Systems&Control Letters,2013,62(1):77−84
13 He De-Feng.Stabilizing economic model predictive control of constrained nonlinear systems.Acta Automatica Sinica,2016,42(11):1680−1690(何德峰.约束非线性系统稳定经济模型预测控制.自动化学报,2016,42(11):1680−1690)
14 He D F,Sun J,Yu L.Economic MPC with a contractive constraint for nonlinear systems.International Journal of Robust and Nonlinear Control,2016,26(18):4072−4087
15 Liu S,Liu J F.Economic model predictive control for scheduled switching operations.In:Proceedings of the 2016 American Control Conference(ACC).Boston,MA,USA:IEEE,2016.1784−1789
16 Liu S,Liu J F.Economic model predictive control with extended horizon.Automatica,2016,73:180−192
17 Angeli D,Amrit R,Rawlings J B.On average performance and stability of economic model predictive control.IEEE Transactions on Automatic Control,2012,57(7):1615−1626
19 Flores-Tlacuahuac A,Moreno S T,Biegler L T.Global optimization of highly nonlinear dynamic systems.Industrial&Engineering Chemistry Research,2008,47(8):2643−2655
