不确定系统的鲁棒与随机模型预测控制算法比较研究
2017-03-10谢澜涛谢磊苏宏业
谢澜涛 谢磊 苏宏业
模型预测控制(Model predictive control,MPC)指的是一类通过显式的系统过程模型来预测其未来响应并求解能使系统表现最优的输入量的计算机算法的总称[1−2].MPC的思想最早可追溯到十九世纪六十年代.由于MPC概念简单,并且能够有效地处理复杂系统的约束问题,实现复杂控制目标,使得MPC在过程工业、汽车、能源、环境、航空、医疗等一系列领域取得了广泛的应用[2−5].MPC的一般工作流程可概括如下:1)在当前时刻,获取系统状态测量值;2)求解一个优化控制问题(Optimal control problem,OCP)得到预测时域控制率;3)仅将预测时域中第一个控制量作为系统输入;4)在下一时刻再回到1).这个过程被一直重复进行,因此MPC又叫做滚动时域控制.
能否准确对系统的未来响应进行预测将直接影响MPC应用的效果,而预测的准确性又取决于系统模型是否准确.模型的不确定性有时会导致被控系统反应迟钝,甚至不稳定[6].虽然滚动时域的方式使得MPC具有一定的鲁棒性[5],但传统的MPC并不是为处理系统不确定性而设计的,其鲁棒稳定性的实现要求外部噪声足够小或者状态约束不存在[7],所以它仍然无法满足一般情况下不确定系统控制的需求.为了系统地解决这个问题,Campo等在1987年率先提出了Min-max鲁棒模型预测控制(Robust model predictive control,RMPC)的算法[8],随后Allwright等在文献[9−10]中将这种Min-max RMPC的思想进一步完善.Min-max RMPC考虑了由不确定性引起的“最坏”的情况,如果系统能在这种“最坏”的情况下稳定运行,则对于未来发生的任何一种不确定性,系统仍然可以稳定运行[11−12].虽然这种考虑“最坏”情况的设计方法使得约束能被所有不确定性所满足,但这种方法却是十分保守的,甚至会导致控制问题不可解.在Min-max RMPC算法发展同时,Blanchini和Kouvaritakis等为处理系统的不确定性提出了另一种基于Tube的RMPC算法[13−15].早期的基于Tube的算法和Min-max算法一样,也十分的保守.为了减少考虑不确定性带来的保守性,Rakovi和Cannon等近期提出了新型的基于Tube的RMPC算法[16−21],通过采用分离控制策略,将名义系统(无不确定性系统)从实际系统中分离出来,把对实际系统的控制转化为对名义系统的控制,把系统状态控制在一个状态约束的子集当中,这个子集就是所谓的Tube.Tube的存在保证了实际系统对约束的满足,这种特性使得设计更简单快速的算法成为可能.
系统中的不确定性也可以看作噪声.RMPC算法只能处理有界、确定噪声,并且要求约束也是有界的.如果把随机噪声当作确定有界干扰来处理,会使得控制器过于保守,较大的随机噪声分布范围甚至会导致RMPC控制器找不到可行解.随机模型预测控制(Stochastic MPC,SMPC)利用了噪声的随机特性并且能处理更多约束类型.在SMPC算法当中,人们通常求取的是惩罚函数的最小期望值[7],而用到的随机特性通常是噪声的期望和协方差(如文献[22−23]),有时还会用到噪声的概率密度分布函数(如文献[24−25]).对于无界噪声,SMPC算法一般考虑以下三种约束:均值约束[26]、概率约束(又叫机会约束)[18,22]和有界输入约束[27−28].这种情况下,SMPC算法设计难点在于处理无界噪声,因为噪声的无界特性会在下一时刻将系统状态拉至过远而导致相关OCP没有可行解.当然,SMPC也是可以处理有界噪声下的有界状态约束的,只要把概率约束中的概率当作1来处理,例如文献[18]和[29].
RMPC和SMPC算法主要研究的是参数不确定性、外部不确定性或结构不确定性,结构不确定性可以转化为参数不确定处理[30].本文主要讨论外部不确定性,读者可以将处理外部不确定性的一些方法拓展到参数不确定性或者更复杂的情况上去.例如,当线性系统中参数和外部不确定性都出现时,在RMPC算法中可以通过将两种不确定性分离,并通过适当的LMI转换就可以进行求解[31],而在SMPC算法中也有类似的通过情景优化的方法来解决[32].
本文的目的在于归纳总结和分析各种典型的RMPC和SMPC算法(如图1所示),揭示这些算法的特点,并对可以用于相同控制对象的算法以表1为依据通过仿真实例来比较算法的优劣.在前文已经介绍了MPC、RMPC和SMPC的主要特点,在下一节将介绍两大类主要的RMPC算法,并通过一个2维的仿真实例展示各种算法的特性.然后,探究4种主要的SMPC算法,并通过一个7维的仿真实例来展示各种算法的不同.最后,通过这些算法的应用来说明这些算法使用的广泛性,并总结和展望RMPC和SMPC的一些未来可研究方向.

图1 主要讨论算法Fig.1 Main algorithms

表1 算法主要参数Table 1 Main parameters of algorithms
符号和定义:正整数集和实数集分别表示为N和R.N[a,b]={a,a+1,···,b}表示从a到b的整数集.X表示一个集合,则表示向量由n个分量组成,且每个分量xi∈X,i=1,···,n.对于集合X⊆Rn和Y⊆Rn,Minkowski集合加法定义为X⊕Y={x+y|x∈X,y∈Y},x+X表示{x}⊕X.Pontryagin几何减法定义为X⊖Y={x|x⊕Y⊆X}.对于α∈R(M∈Rm×n),αX(MX):={αx(Mx)|x∈X}.co{v1,v2,···,vn}表示点集{v1,v2,···,vn}的凸包.E(·)表示期望,Exk(·)表示给定xk的条件期望,Pr(·)表示概率.‖·‖表示标准欧几里得范数,‖ ·‖1表示ℓ1范数,‖ ·‖∞表示ℓ∞范数. 对于n×1的矩阵M(w)={m1(w),···,mn(w)}T和
1 鲁棒模型预测控制(RMPC)
鲁棒模型预测控制处理的是一类有界噪声问题,带外部噪声的线性不确定系统可表示为[12,33−36]:
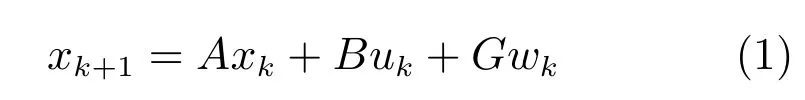
其中,系统状态xk∈Rn,系统输入uk∈Rm,外部噪声wk∈Rr.外部噪声w的值在时刻k和未来时刻都是未知的,只知道它的取值范围,而且(不失一般性)可以表示为:
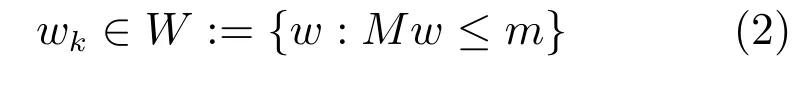
一些文献(如文献[34−37])处理的外部噪声取值范围为∞范数类型(即‖w‖∞≤∈),这可以看作是式(2)的一种特殊情况.外部噪声可能来自于周围环境噪声,也可能来自于对模型失配部分的重构.RMPC中的约束通常都是包含原点的凸集,设闭合凸集X={x|Exx≤1},U={u|Euu≤1},则系统的状态约束和输入约束可分别表示为:

部分如文献(如文献[34−35])会考虑u和x的联合约束(即Exx+Euu≤1).联合约束在表达上更具一般性,但它不利于体现外部干扰在不同控制率下对输入约束和状态约束的影响,同时也不利于应用到基于Tube的算法当中.在实际应用中,独立的约束更常见,所以之后的章节中不对联合约束的情况进行讨论.
1.1 Min-max RMPC
如文献[33]所描述,Min-max RMPC的OCP一般可表示为:

其中输入约束U={u|Euu≤1},状态约束X={x|Exx≤1},终值约束XN={x|Efx≤1},JN(x)=xTPx为终值惩罚,N为预测时域,Q,R为权重正定矩阵.

式中其他矩阵的定义在此省略.为了求解式(5),通常将这样一种Min-max形式的OCP转化成为标准的优化问题,如LP、QP或者SDP.转化的困难主要来源于两方面:一是怎样处理Min-max形式的目标函数;二是怎样让约束摆脱噪声的干扰.为了解决这两个问题,学者们做了很多的努力,这里总结比较常用的策略:
S1目标函数:将Min-max形的目标函数由

决策变量c可以被当作是max(·)部分的上界.文献[8]利用枚举法列举WN所有的顶点,将式(6)中的约束转化为其中是由WN所有顶点组成的集合,nv为顶点的个数.枚举顶点法实质上是基于这样一个性质[38]:如果C为闭合凸集且f:C→R为凸函数,若f在C上存在最大值,那么这个最大值将在C的某个极点处取得.文献[30,34]利用Schur补将式(6)中的约束转化为一个不确定的线性矩阵不等式(LMI),然后通过一个半定松弛过程(具体见文献[39])将不确定LMI转化为确定的LMI.由于枚举法引入的约束随着w的维数和预测时域N的增加而急剧增加,导致OCP的求解速度变得非常缓慢,所以在实际应用中并不是一个很好的选择,而LMI则没有这样的问题.
S2约束处理:通过枚举WN所有顶点的方法(如文献[8])可以保证“最坏”的情况也能够被满足,或将原约束分离为确定和不确定两部分,通过运行一个局部优化问题求解不确定部分的最大值,即“最坏”情况(如文献[39−40]):

决策变量是否出现在不确定部分会使得求解maxw{不确定部分}的方法略有不同.同样,对于约束的处理,枚举法会使得OCP的约束数量急剧增加,而局部优化求解的方法则没有这方面的问题.
Min-max RMPC算法根据控制率是否为与系统状态相关的函数(即u=ϕ(x),其中ϕ(x)通常是仿射的)可分为开环和闭环两大类.如图2所示,在本文中把控制序列为{uk+j}的算法称为开环Minmax(Open-loop min-max,OL2M)RMPC,如文献[8,10];把控制率为uk+j=Kxk+j+vk+j(其中vk+j为新的决策变量,K为反馈矩阵)的算法称为定常反馈Min-max(Fixed feedback min-max,FF2M)RMPC,如文献[33,41];控制率为uk+j=Kjxk+j+vk+j(其中Kj也是决策变量)的算法称为动态反馈Min-max(Dynamic feedback min-max,DF2M)RMPC,如文献[34,42];双模式枚举Minmax(Dual mode enumeration min-max,DME2M)RMPC特指由Scokaert和Mayne在1998年提出的一种控制率uk+j=f(wk,l,wk+1,l,···,wk+j−1,l)的算法,其中f(·)为一个非线性函数,{wk+j,l}为W的各个顶点,详见文献[12].这些算法都采用了S1和S2提及的策略来处理Min-max的OCP问题,它们的特点将在后面进行讨论.
开环Min-max(Open-loop min-max,OL2M)RMPC:作为最简单的控制结构,OL2M RMPC的OCP中的决策变量为通过利用S1和S2,Min-max OCP可以被转化为一个标准的LP问题(如文献[8])或SDP问题(如文献[39]).
定常反馈Min-max(Fixed feedback min-max,FF2M)RMPC:在经典控制论中使用闭环回路往往可以实现更好的控制效果,模型预测中采用反馈校正的方法也能实现闭环回路.反馈的关键是利用可测量的系统状态信息,对原预测系统进行矫正.另一种利用系统状态信息的方法是在输入中直接引入状态信息,FF2M RMPC就是这样一种闭环控制算法,控制率uk+j=Kxk+j+vk+j为系统状态的线性函数,通常选取能使得A+BK幂零的K[33],即存在特定的整数s使得(A+BK)s=0.这种定常反馈的好处在文献[41]中已经进行了详细的叙述,总的来说就是反馈的存在使得式(7)中的maxw{不确定部分}部分在一定程度上得到抑制,从而使得约束得以放宽,降低了保守性.但是,由此并不能断言FF2M RMPC一定比OL2M RMPC好,因为这种约束的放宽往往是针对状态约束而言的,而对于输入约束,由于反馈的存在,使得干扰也进入了输入,从而导致经过局部优化后的输入约束变得更加狭小.比较极端的情况是,输入约束本来就很小,而干扰比较大,经过S2的局部优化后输入约束会变为空集从而导致OCP不可解.同样,FF2M RMPC的OCP也可被转化为一个标准的LP或SDP问题.
动态反馈Min-max(Dynamic feedback minmax,DF2M)RMPC:在反馈控制中,K的选择将极大地影响控制效果,为了综合K的选取与控制器的设计,一种自然的想法是将反馈矩阵K也设置成决策变量,控制率则变为uk+j=Kjxk+j+vk+j.动态反馈使得OCP的自由度增加,使得保守性得以降低.事实上,OL2M RMPC和FF2M RMPC分别属于DF2M RMPC的一种特殊情况,当Kj=0,∀j时,则为 OL2M RMPC,当Kj=K,∀j时则为FF2M RMPC.
但不幸的是,控制率uk+j=Kjxk+j+vk+j并不能直接应用于OCP(4),它会使得OCP(4)变成非凸问题.在发现控制率uk+j=Kjxk+j+vk+j实质上是干扰w的函数后,文献[34]提出了干扰仿射控制率文献[42]则进一步证明了干扰仿射控制率和状态仿射控制率实际存在着一一对应关系,而更有利的是,干扰仿射控制率能继续保持原OCP的凸特性,所以一般用干扰仿射来代替状态仿射的情况.
双模式枚举Min-max(Dual mode enumeration min-max,DME2M)RMPC:Scokaert和Mayne在文献[12]中提出了一种DME2M RMPC的算法.这种算法本质上是一种开环算法,不同的干扰实现对应着不同的决策变量,同时利用了双模策略来保证了算法的可行性与稳定性.双模算法是一种被广泛应用的确保可行与稳定性的算法,如基于Tube的算法[19−20,43]或基于动态规划的算法[44−45].在双模算法当中,有个概念是十分重要的:
鲁棒控制不变(Robust control invariant,RCI)集[12,46]:
如果需要满足约束X和U的系统(1)在控制率uk=Kxk和初始状态xk∈S的情况下满足Kxk∈U且(A+BK)xk+Gwk∈S,∀wk∈W,则集合S⊆X⊆Rn叫做鲁棒控制不变(RCI)集,K可离线计算得到.
注意.文献中有很多种对于不变集的定义,例如文献[31]把如上这样的集合S叫做正鲁棒不变(Robustly positively invariant,RPI)集,而文献[16]和[46]又用正鲁棒不变(RPI)集来定义不需要满足状态反馈控制率和系统约束的不变集,为了避免混淆,本文中鲁棒控制不变(RCI)集指的是如文献[12,46]中所定义的集合.
在DME2M RMPC算法中,S为RCI集,则双模算法可概括为:
·如果xk/∈S,“外部控制器”作用,通过求解相应的OCP,将x引导至S中.
·如果xk∈S,“内部控制器”作用,不需求解任何OCP,直接将输入设置为uk=Kxk,K为与RCI集S相关的反馈矩阵.由RCI集的特性可知,系统状态将始终处于S中,并最终趋于稳定.
文献[12]中的“外部控制器”实质上求解的是一个开环OCP问题.对于预测时域为N的控制器,噪声W的所有顶点实现可用集合表示,其中nv为w顶点的数目,表示nv的N次幂,Wv为W所有顶点的集合.每一种顶点实现Wl都有与之对应的决策序列和相应的状态序列则“外部控制器”求解的OCP可描述见附录中的(A1).
式(A1)是已经枚举过的开环OCP,通过策略S1可以很容易地进行求解.由于不同的噪声顶点实现对应不同的决策组合,使得OCP的自由度比一般开环OCP更高,所以这种双模枚举的算法保守性会更低.可以看到,由于噪声顶点实现有种组合,所以决策变量数由普通开环OCP的N×m个提高到个,但如果没有因果约束的限制,即使求解出所有的决策变量,控制器也不知道选择哪一个输入给系统,且系统稳定性也无法保证,所以文献[12]用因果约束又将决策变量数目降低到个.由前文知,这种顶点实现决定决策变量的方法也可应用到闭环控制策略中,但由于它仍属于枚举法,当N增大,或噪声维数增多时,计算量过于庞大,导致此种算法并不实用.但这种DME2M RMPC算法的意义非凡,它提供了一种直观地确保可行性和稳定性的双模结构,被后期大量的学者和算法广泛采用.
可行性与稳定性:算法可行性是指对应OCP有可行解的特性,对于RMPC来说,算法可行性往往与系统的约束以及噪声的取值范围有关.OCP(4)可行的必要条件为:

可行必要条件指出了系统约束和噪声的取值范围需满足的关系式,它在系统设计阶段能给予设计者很好的帮助.例如,通过Matlab的MPT工具箱[47],很容易对式(8)中的关系进行测试.如果条件没有满足,则无论设计什么样的模型预测控制器,系统的递归可行性都是没有办法保证的.设计者就不需要花费时间去调试不同的算法和设计不同控制率上,而是把精力放在如何从硬件或周围环境上降低噪声范围,如何扩大输入约束,或者扩大状态约束上.
当提及稳定性的时候,是以算法的可行性为前提的.以上算法中,除了DME2M,还没有讨论稳定性所需要满足的条件.系统稳定性可通过终值约束和终值惩罚满足一定条件来实现[48],或者使用无穷预测时域[32−33],但通过无穷预测时域实现的稳定性往往要求系统为渐进稳定系统或者系统矩阵(A,B)可控.为了保证OL2M,FF2M,DF2M RMPC的稳定性,终值惩罚JN(x)=xTPx和终值约束XN需满足[39,48]:A1:XN为RCI集;A2:当uk=Kxk时,对于∀xk∈XN和∀wk∈W有如果不考虑稳定性,仅保证算法的递归可行性的话,A1就足够了.

表2 Min-max算法的问题规模Table 2 Problem scale of algorithms
最大的RCI集:为了降低算法的保守性,XN需要尽可能大.当uk=Kxk,且需满足约束X和U时,系统(1)的最大的RCI集SM可如下求出[31]:

同样的,最大的控制不变(Control invariant,CI)集S0M可以通过令用同样的方法求得.如果对于需满足约束X和U的系统(1)满足:S0⊆X,KS0⊆U且(A+BK)S0⊆S0,则S0叫做控制不变(CI)集,更多和不变集的相关信息可查阅综述文献[46].
Min-max算法的问题规模总结如表2,其中带∗表示求解中利用枚举法进行转化.
参数不确定系统处理的是形如minumax(A,B)∈ΩJ(x,u),s.t.xk+1=Axk+Buk,x∈X,u∈U的问题[49],其中参数不确定集 Ω =co{(A1,B1),···,(Ano,Bno)}.一种自然的想法是类似外部不确定问题那样采用枚举法,然而参数不确定性使得优化问题对(A,B)是非凸的,枚举法并不能保证目标函数的最优和约束的满足.文献[30]利用不变椭圆集和LMI解决了上述问题.具体过程可分为三步:1)将预测时域设置为无穷大,并作相关假设保证惩罚函数有上界;2)采用反馈控制率u=Kx,其中为决策变量,并建立使惩罚函数上界相关不等式得以满足的LMI;3)在u=Kx作用下,未来状态实际上都会保持在不变椭圆集P(Qp)中,再建立使P(Qp)⊆X和KP(Qp)⊆U成立的LMI.这样原问题就被转化成了SDP问题,同时不变集和无穷时域的应用保证了递归可行性和稳定性.文献[30]的这种方法被大量学者处理RMPC问题或LPV问题所采用,如文献[50−53].
1.2 基于Tube的RMPC
基于Tube的RMPC首先由文献[13]提出,之后被文献[15,19−20,43,54−55]等所发展.其基本思想是通过某种控制率将系统的状态xk+j控制在一个可以叫做Tube的集合Xk+j中,这个Tube集合为系统约束X的子集,然后将整个Tube引导至一个希望的位置.这种对于Tube的操作让人们可以直接处理不确定性所带来的对于系统动态和约束的影响[56].此算法的一大优势是可以将系统确定部分和不确定部分分离,使得控制器可以将很多工作离线计算完成,这个特点使基于Tube的算法得到广泛发展和应用.本文讨论三种典型的基于Tube的RMPC算法(如图3所示):基于Rigid tube(RT)的RMPC[55],基于Homethetic tube(HT)的RMPC[19]和基于Parameterized tube(PT)的RMPC[20].
图3 基于Tube的RMPCFig.3 Tube-based RMPC
对于这些基于Tube的RMPC,可以给出一个通用的OCP:
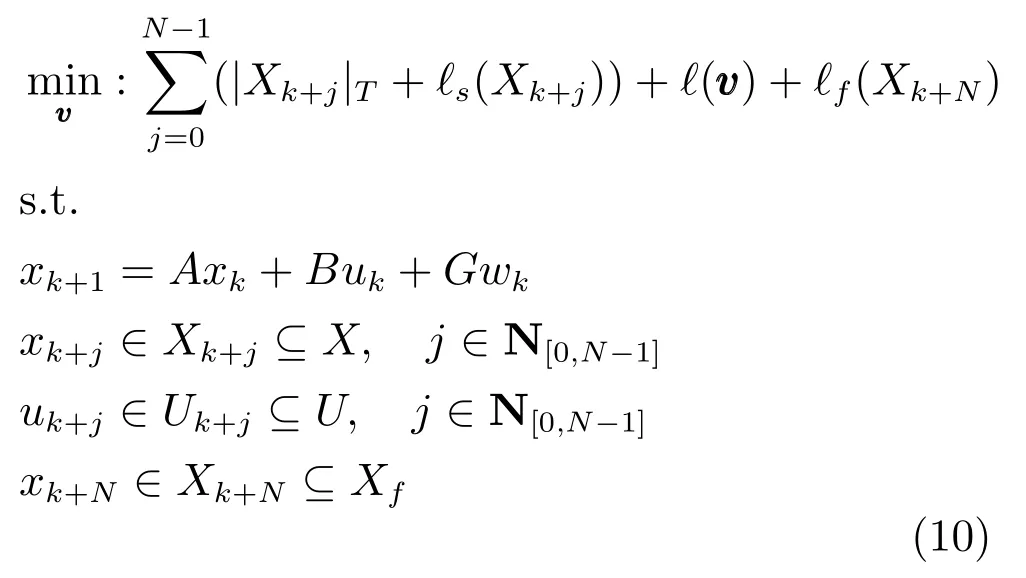
其中|Xk+j|T表示从Xk+j到目标集合T距离的测度,可以叫做“位置控制”.ℓs(Xk+j)表示对集合Xk+j形状(包括大小)的惩罚,可以叫做“形状控制”.表示对决策变量的惩罚.为终值惩罚.
RT和HT RMPC中的T为{0},而PT RMPC中为一个RCI集S.约束xk+j∈Xk+j⊆X需要被分为xk+j∈Xk+j和Xk+j⊆X两部分来单独处理,通常用所属递归法
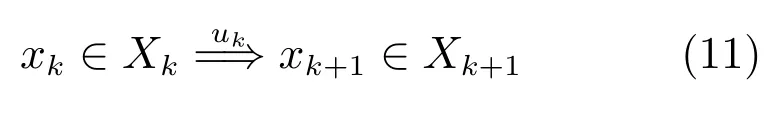
来保证系统状态待在对应Tube中,即xk+j∈Xk+j,第二部分则可直接通过约束Xk+j⊆X保证.uk+j∈Uk+j⊆U同样可直接在约束中保证.
各种算法对于Tube的控制各不相同,在RT RMPC中,只通过控制Tube的中心来控制Tube的位置,如图4(a)所示.在HT RMPC中,Tube的位置和大小同时都可被控制,如图4(b)所示.而PT RMPC提供了更多的自由度,通过控制Tube的顶点,不仅可以控制Tube的位置和大小,还可以控制其形状,如图4(c)所示.
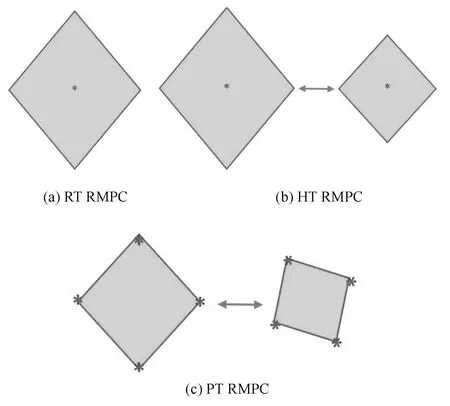
图4 对于Tube的控制Fig.4 Manipulation of tubes
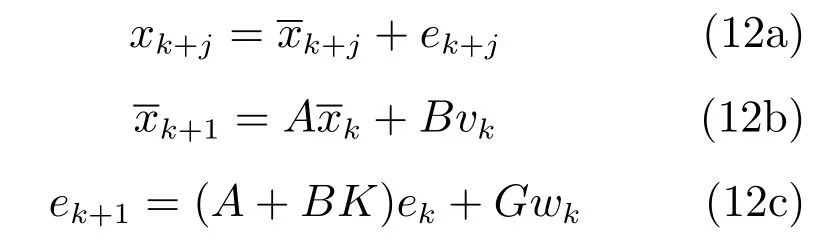
其中式(12b)为名义系统模型,式(12c)为不确定部分.当K被时变参数Kk+j代替时,式(12)仍然成立,只需把式(12c)替换为ek+1=(A+BKk)ek+Gwk.PT RMPC采用了更为复杂的参数化控制策略,但它仍然是基于名义系统(12b)的.这三种算法的目标函数都不包含不确定部分的,更多细节将随后讨论.
Righid tube(RT)RMPC:由于控制率可以将不确定系统进行分离,得到确定的名义系统部分和不确定的噪声部分.文献[55]由此设计了只需控制确定的名义系统状态的RT RMPC算法.RT RMPC中的Tube形式为其中Sr为正鲁棒不变(RPI)集[16]:
正鲁棒不变(Robustly positively invariant,RPI)集:集合Sr叫做系统(1)的正鲁棒不变集,如果当uk=Kxk时,对于∀xk∈Sr和∀wk∈W有(A+BK)xk+Gwk∈Sr成立.
在控制率的作用下,有(A+BK)Sr+GW⊆Sr成立,所以所属递归式 (11)自然成立.由于Xk+j和Uk+j需要分别为X和U的子集,所以希望Sr尽可能小,系统(1)的最小RPI集可通过求得[57],或通过近似求得[16],其中r和ρ∈[0,1)满足(A+BK)rGW⊆ρGW.其实,直接使用Sr是十分保守的,一种有效地降低保守性的方法是令相比于使用无穷时域的RPI集,这里得到的Tube将会更小.但这种方法的提升和PT RMPC比起来,效果是有限的,所以没有学者单独以此提出过一种算法.

因此,RT RMPC的OCP可见附录中的(A2).
文献[31]提出了一种等价于文献[55]中RT RMPC的不同表达式,这种方法里利用了系统(1)的分解模型:
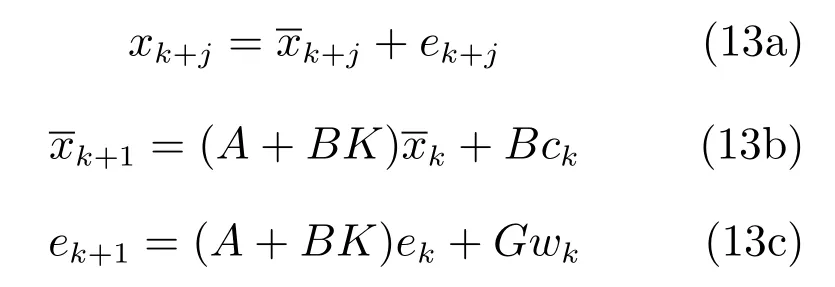
其中uk+j=Kxk+j+ck+j.注意式(13b)和(12b)之间的不同,这种分解模型在基于Tube的SMPC中同样被广泛应用.
Homethetic tube(HT)RMPC:由于RT RMPC算法中Tube的大小是不能改变的,且Tube在设计的过程中过度地考虑了未来所有时刻噪声的影响,使得Tube体积较大,保守性太强,所以文献[19]设计了一种Tube大小可控的HT RMPC算法.在控制率下,HT RMPC中Tube为和(其中决策变量αk+j≥0).集合Sr同样为RPI集.
在HT RMPC中,所属递归式(11)并不能单独靠控制率而得到.由于控制Tube大小的决策变量αk+j的存在,同样的控制率并不能保证(A+BK)αk+jSr+GW⊆αk+j+1Sr,需要显示地将之作为约束条件加入到OCP中才能保证所属递归式(11)成立.

HT RMPC的最终OCP可见附录中的(A3).
Parameterized tube(PT)RMPC:HT RMPC使得Tube算法的保守性在一定程度上得到了降低,但仍存在两个问题,一是Tube可能在某些方向上还有缩小的可能;二是如果系统约束和Tube不在相同的朝向,即使Tube体积很小,但在某些方向上仍会使得紧缩后的系统约束没有多少余量.PT RMPC就是解决了这两个问题的一种算法.在PT RMPC中的Tube和控制率更为复杂,这种复杂给求解OCP提供了更多的自由度.根据文献[20],W被描述为其中q为W的顶点数.为了保证稳定性,OCP中的终值约束为一个RCI集S={x:Esx≤1},Tube和控制率如表3所示.
通过这样的参数化,可确保xk+j∈Xk+j和uk+j∈Uk+j,且参数满足
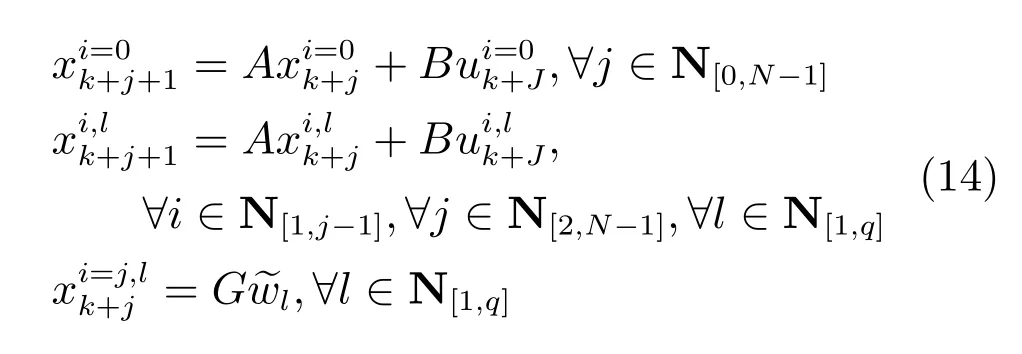
PT RMPC中的目标集合T为终值约束S.点到集合距离测度有许多不同的定义,如文献[20,31],这里讨论容易理解的文献[31]中的定义:
点 到集合的距离:如果x∈S则|x|S=0,否则|x|S=max{Esx}−1.所以集合X到S的距离定义为|X|S=maxx∈X|x|S.则PT RMPC中的OCP(10)最终可见附录中的(A4).
基于Tube的RMPC算法的问题规模如表4所示.设集合Xf={x|Efx≤1}和Sr={x|Esrx≤1}的表达为不可约,则nf表示Ef的行数,nsr表示Esr的行数.
各个算法的保守性是不一样的,往往保守性越大,可行域越小.各算法可行域之间的关系可以通过以下定理来说明:
定理1.假设集合A→B表示A⊆B,AB表示在一定条件下A⊆B,对于满足约束X和U的系统(1),以上算法的可行域满足如图5所示关系.

表3 PT RMPC的Tube和参数化Table 3Tubes and parameterization of PT RMPC

表4 基于Tube的RMPC算法的问题规模Table 4 Problem scale tube-based RMPC


1.3 仿真和分析
采用文献中广泛应用的仿真系统模型[17,19,55]:

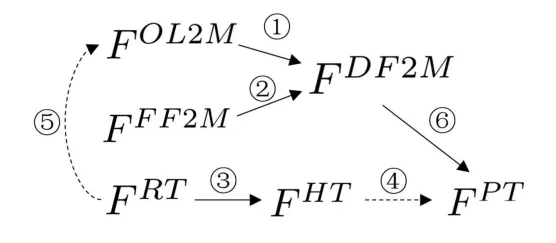
图5 可行域关系Fig.5 Relationships of feasible sets
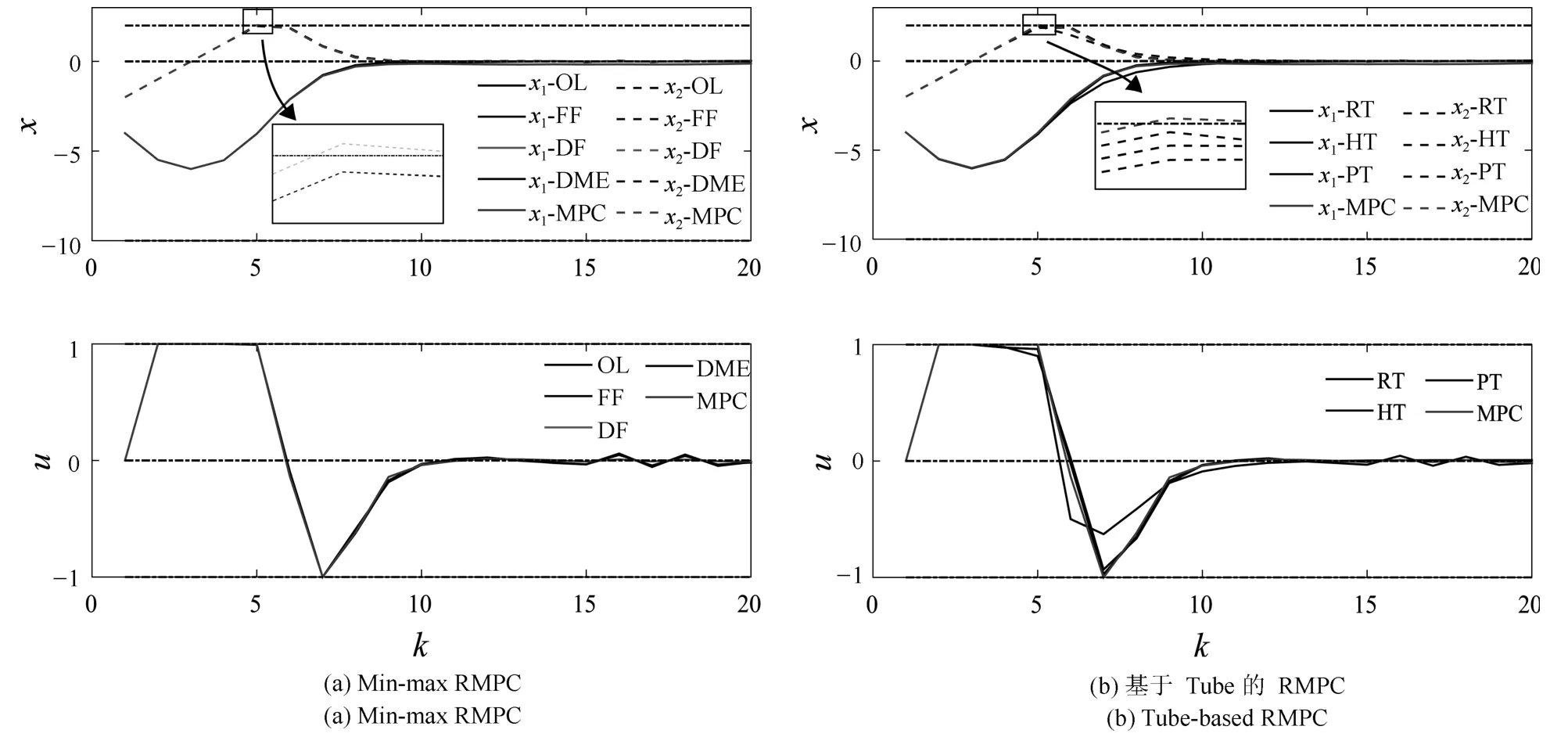
图6 仿真结果Fig.6 Simulation result
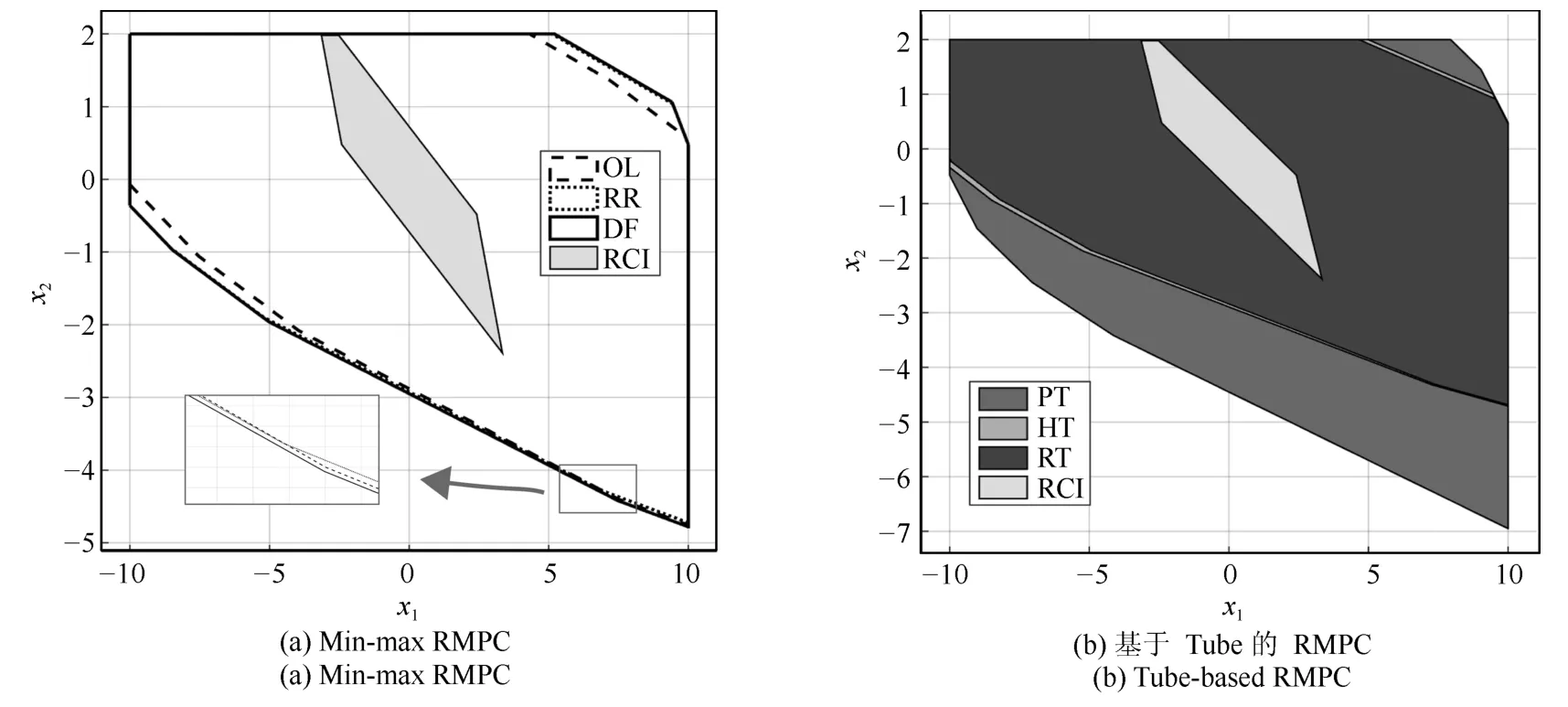
图7 可行域Fig.7 Feasible set

图9 满足条件时OL2M和RT RMPC的可行域Fig.9 Feasible sets of OL2M and RT RMPC under condition

图10 DF2M和PT RMPC的可行域Fig.10 Feasible sets of DF2M and PT RMPC
选择控制时域为N=5,仿真时域为TN=20.仿真结果和可行域如图6~图10所示.从图6可以看到所有RMPC算法都满足约束要求(曲线几乎重合),而MPC算法则违反了约束.从图7(a)可以看到FOL2M⊆FDF2M和FFF2M⊆FDF2M.DME2M RMPC算法作为一种特殊的开环算法,通过增加OCP的自由度使得其可行域也得以扩大,在本例中,FDME2M=FDF2M,但是其变量数目,特别是约束数目太多,使得求解平均用时为88.9s,远远高于其他非枚举算法.从图8~图9可以看到,当XfSc时,不能保证FRT⊆FOL2M,而如图9(b)所示,当Xf⊆Sc时,有FRT⊆FOL2M.所有仿真结果都符合定理1.
仿真由CPU为Intel(R)Core(TM)i7-4600@2.1GHz 2.7GHz的电脑完成,从表5和可行域图中可以看到以下规律:
1)有效的决策变量越多,可行域越大.
2)同类型算法结构下(Min-max或者基于Tube的算法),变量数目和约束数目越多,平均CPU时间就越大.
由于PT RMPC的终值约束为RCI集,所以可以将DME2M RMPC中的双模式方法直接应用到PT RMPC中,即一旦xk进入RCI集,就直接启用控制输入uk=Kxk.双模式方法的启用可以大大缩短平均计算时间,在此例中,双模式方法下的PT RMPC算法平均CPU时间为0.16s.
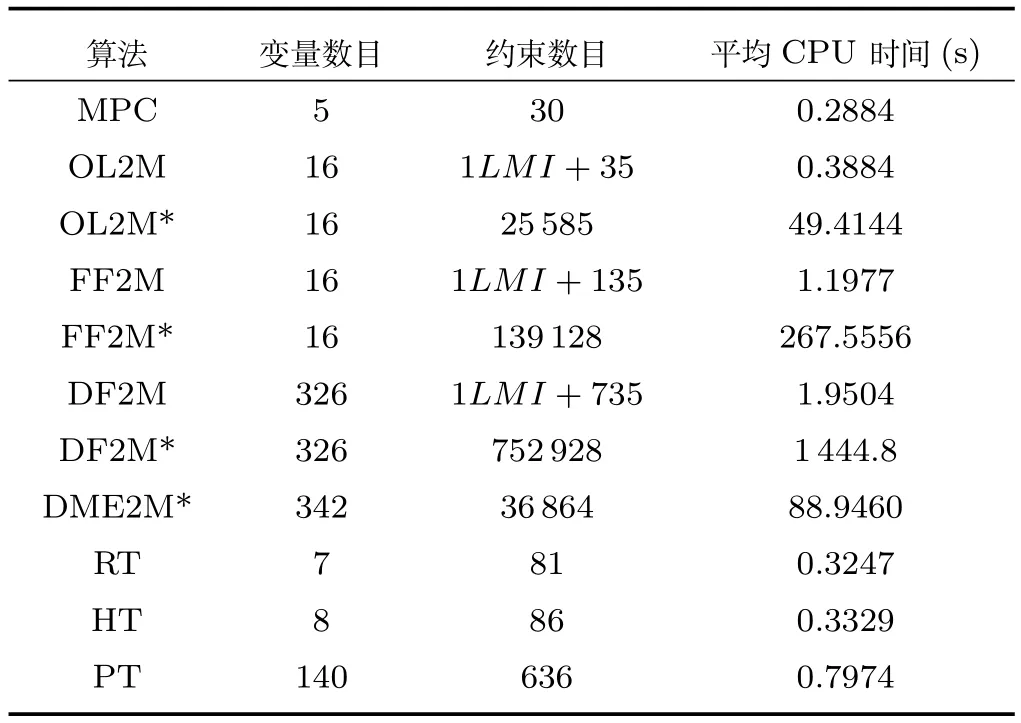
表5 RMPC算法对比Table 5 Comparison of RMPC algorithms
2 随机模型预测控制(SMPC)
随机模型预测控制利用噪声的统计特性来实现控制目标,能够有效地处理机会约束或者有界约束下的系统控制问题.由于机会约束系统在一定程度上允许约束被违反,它通常对噪声的取值范围是不敏感的.而对于有界约束系统,无界噪声的出现往往给系统控制带来巨大的挑战.本文讨论应用较为广泛的基于情景生成法、基于随机Tube和基于确定性等价式的SMPC算法,以及一种处理有界约束系统下无界噪声的SMPC算法.各算法处理的约束和噪声类型如表6所示.
SMPC的OCP的一般形式表示如下[5,32,65]:


表6 主要SMPC算法Table 6 Main SMPC algorithms
2.1 基于情景生成的(Scenario generation,SG)SMPC
情景生成法实质上是一种随机规划中的随机模拟技术,基于SG的SMPC由Cala fiore和Campi在2005年提出[58].这一类方法利用干扰概率密度函数对独立同分布(Independent identically distributed,IID)的干扰进行大量的采样(这些采样也可以叫做情景),来构造一个基于情景的OCP,当情景数目达到一定量时(这个数目往往是可以定量确定的),情景OCP的解能在较大概率上成为原OPC的解.和基于采样的(Sample-based)算法(如文献[66−67])不同的是,基于采样的算法通过对干扰采样并利用大数定理来估算扰动的期望以及概率分布,构建基于期望和概率(而不是采样)的OCP,且基于采样的算法往往无法确定合适的采样数目.
研究基于SG的SMPC的稳定性的文献比较少,学者们更多关注的是算法的可行性和最优性,例如文献[68−69].因此,式(16)中的终值约束和终值惩罚常常被省略.对于基于干扰仿射反馈和状态仿射反馈的控制率来说,OCP(16)可以被转化为文献[58−59]中所描述的基于SG算法的一般形式:
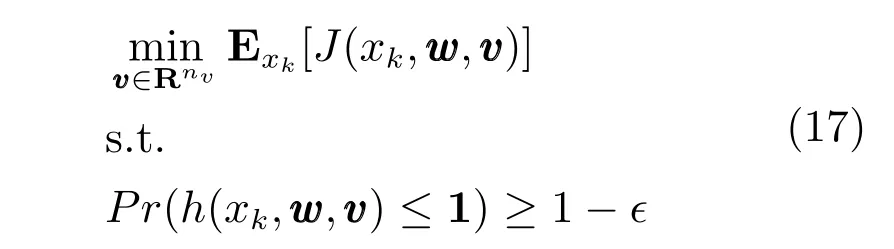
其中v为nv-维的决策变量,w为干扰向量.基于SG的SMPC要求J(xk, w, v)和h(xk, w, v)对于v来说是凸的,而对IID干扰的概率密度分布没有要求,所以这种方法也可以用到参数不确定问题上.通过采样,随机OPC(17)可用情景OCP替代:


2.2 基于随机Tube的(Stochastic tube,ST)SMPC
基于ST的SMPC主要由文献[18,29,61]提出,算法具有以下特点:1)只能处理有界噪声(即w∈W),例如,截断正态分布噪声;2)控制率为u=Kx+c且利用了分解模型(13);3)采用双模式控制策略和无限预测时域(即N→+∞)来保证可行性和稳定性,所以式(16)中的终值约束JN(xk+N)=0.算法允许∈=0.文献[18]和[29]中只处理了状态约束,但是由于反馈控制率u=Kx+c使输入中引入了状态,使得输入约束也可以被用类似方法处理,如文献[61].接下来,仅用状态约束来介绍基于ST的SMPC的算法的基本原理.

2.3 基于饱和函数的(Saturation functions,SF)SMPC
基于SF的SMPC最先由Hokayem在文献[24]中提出,文献 [24]适用于Schur稳定系统(即|λi(A)|<1,i∈N[1,n]),文献 [25]将之扩展到 Lyapunov稳定系统(即|λi(A)|≤1,i∈N[1,n],其中某些|λj(A)|=1).文献 [27]则进一步将该方法应用到系统状态不可测的情况下,其主要方法是通过观测器来估算当前系统状态值.

对于Lypunov稳定系统,文献[25]将系统矩阵(A,B)转化为的形式,其中As为Schur稳定Ao为正交阵,且λ(Ao)=1.为了保证系统具有和文献[24]一样的稳定性,文献[25]对正交部分增加了“负漂移条件”的约束,且假设Umax≥U∗也需要成立,其中U∗为和“负漂移条件”相关的一个常量.
2.4 基于确定性等价式的(Deterministic equivalents,DE)SMPC
确定性等价式是随机规划中处理机会约束的一种常用方法,文献[62]将之应用到模型预测控制中.基于确定性等价式的SMPC有两大特点,一是利用确定性等价式将机会约束转化为确定约束,二是将目标函数利用状态的期望和协方差迭代式直接表示为确定形式.这样,随机MPC就转化成了确定MPC问题.若已知噪声的期望和协方差,当随机噪声的密度分布可知时,可以利用累积概率函数的反函数将机会约束确定化,如文献[62];而当随机噪声的密度分布不可知时,可利用坎泰利不等式(又叫切比雪夫单边不等式)将将机会约束确定化,这种方法由文献[63]提出,文献[22]更详细地介绍了这种算法并通过引入可选的初始约束来提高算法性能.文献[23]将之扩展到系统状态需要用观测器观测的情形,文献[64]随之又将其进一步扩展到系统带有乘法扰动的情况.
对于线性外部干扰系统,可采用控制率uk+j=

机会约束Pr[Exix≤1]≥1−∈(其中Exi为Ex的第i行)可被替换为:
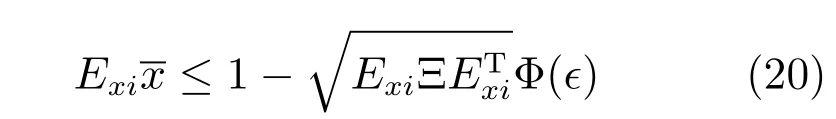
其中,当随机噪声服从正态分布时,式(20)可通过正态分布标准化得到[62],且Φ(∈)=N−1(1−∈),N−1为标准正态分布的累积概率反函数.当噪声的密度分布不可知时,式(20)通过坎泰利不等式得到[63],且由于采用无下标的x,所以也不用下标,当x表示xk时,Ξ相应地表示Ξk.但是式(20)对于Ξ是非线性的,难以直接求解,需要进行线性化:

其中α∈[0,1]为一个自由设计量.由于坎泰利不等式没有用到噪声的密度分布信息,导致其本身是比较保守的,而线性化进一步引入了更多的保守性,这点随后将通过仿真实例展说明.机会输入约束也可以通过类似方法处理得到Ψ(Eui,v,U),其中U=KΞKT.


2.5 仿真实例
仿真模型为一个常压等离子射流仪(APPJ)[74],APPJ的线性化连续模型为式(22):
以采样时间Ts=5对连续模型进行离散化,同时将预测时域选择为N=9,仿真时域TN=50.
由于基于ST的SMPC利用了情景生成法进行求解,这里仅展示基于ST的仿真结果.当X={x|Pr{−6≤x1≤6,−6≤x2≤6,−6≤x3≤6,x4,x5,x6,x7∈R}≥0.8},W={w|w~N(0,0.12),−1≤w≤1},η=0.1,N(nv,∈,η)=(1/∈)(e/(e− 1))(ln(1/η)+nv− 1),x0=(0,0,0,0,0,0,0.8)T时,基于ST的仿真结果如图11所示,可以看到,系统表现没有违反约束.
对于基于SF的SMPC,U={u|Pr{−1≤u1≤1,−1≤u2≤1}≥0.8},Umax=1,x0=(1,1,1,1,1,1,1)T,M=0.1,α=1,仿真结果如图12所示,由于饱和函数的存在,使得无论是在仿真时域还是在预测时域,都没有约束被违反.如果不使用饱和函数,而直接使用反馈率仿真结果如图13所示.可以看到,在仿真时域同样能够满足约束,这是因为uk=vk,并没有噪声被引入第一个输入值.而在预测时域却可以看到输入约束被严重违反,这样就不能保证系统的闭环稳定性了.
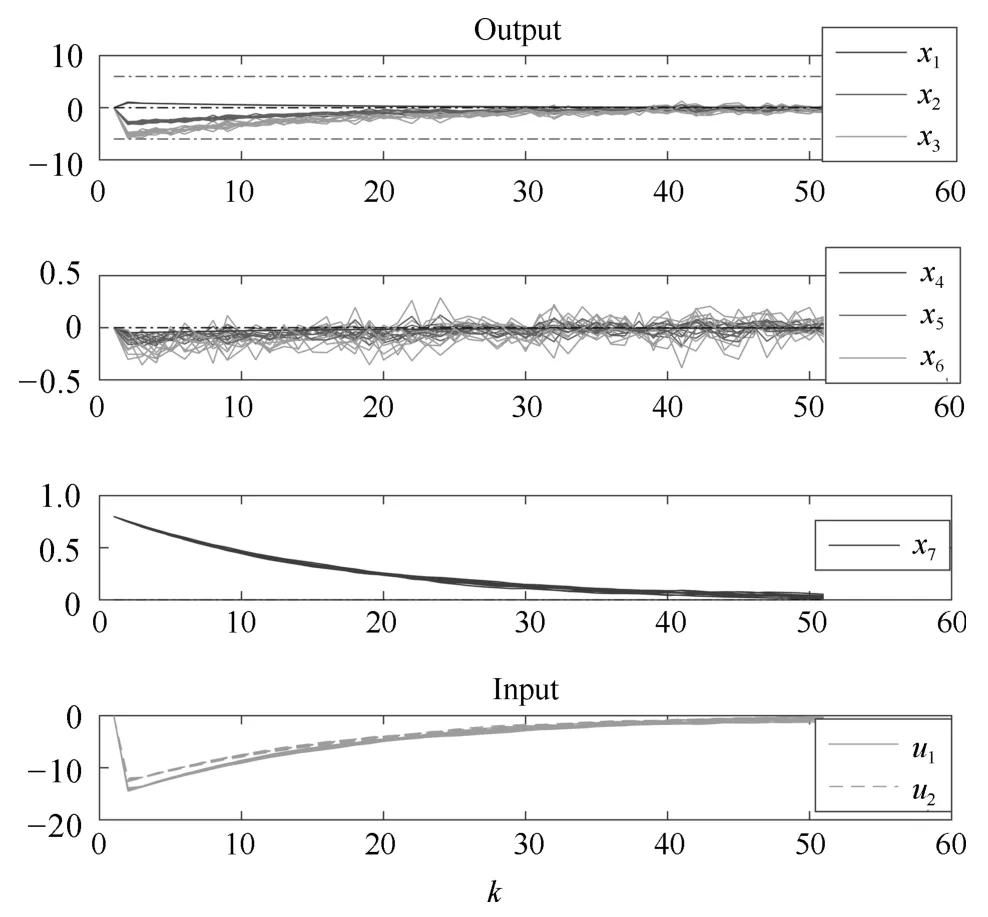
图11 基于ST的SMPCFig.11 ST-based SMPC
对于基于DE的SMPC,X={x|Pr{−4≤x1≤4,−4≤x2≤4,−4≤x3≤4,x4,x5,x6,x7∈R}≥0.8},U={u|Pr{−1≤u1≤1,−1≤u2≤1}≥0.8},W={w|w~N(0,0.12)},x0=(0,0,0,0,0,0,0.2)T.图14(a)展示了100次仿真结果,只有15次违反约束,违反率为15%,满足要求.图14(b)为基于DE的SMPC的可行域,其中红色的为线性化之前的可行域,而蓝色的为线性化之后的,可以看到红色比蓝色大很多,说明线性化后的系统更为保守.

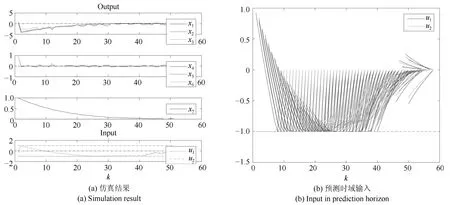
图12 饱和函数下的仿真结果Fig.12 Simulation result with SF

图13 没有饱和函数时的仿真结果Fig.13 Simulation result without SF
3 RMPC和SMPC的应用
随着RMPC算法和SMPC算法的不断发展和日益成熟,使其在各领域得到了较为广泛的应用.表7汇总了近年来(自2010年)本文所讨论的RMPC算法和SMPC算法的部分应用场合.括号内的英文缩写表示应用的算法,其中TB表示基于Tube(Tube-based)的算法,包括本文涉及的RT、HT和PT三种,MM表示Min-max算法,其他SMPC算法缩写和上文一致.可以看到,除了在传统的流程工业中的应用,近年来一些新兴领域,如无人汽车、智能家居、飞行器、机器人、风力发电、水资源、城市交通等都有本文RMPC和SMPC算法的应用场景.同时,在电网、医疗、金融等方面RMPC和SMPC也有不俗的表现.
从表7中可以发现,基于Min-max的RMPC相比于基于Tube的算法应用更为广泛一些,这是因为基于Min-max的算法概念和结构更为简单,易于在复杂实际对象控制中扩展,容易被工程师所接纳和采用.类似的,SMPC的算法中以基于SG和基于DE的算法应用最为广泛,这是因为这两类算法分别代表了随机规划中处理机会约束的两种常用技术,即随机模拟和确定性等价.基于ST的算法在使用过程中也需用到这两种技术来处理其中的子问题,相对较为复杂,且对系统模型更为敏感,应用较少.而基于SF的SMPC算法难以应用于实际对象是因为应用中很少会考虑绝对意义的无界噪声,且该算法仅适用于有界输入约束,而实际应用中常常会伴有状态约束,并且饱和函数的运用使得算法过于局限.但是这种算法弥补了SMPC在有界约束下处理无界噪声的理论空白,具有重要的意义.
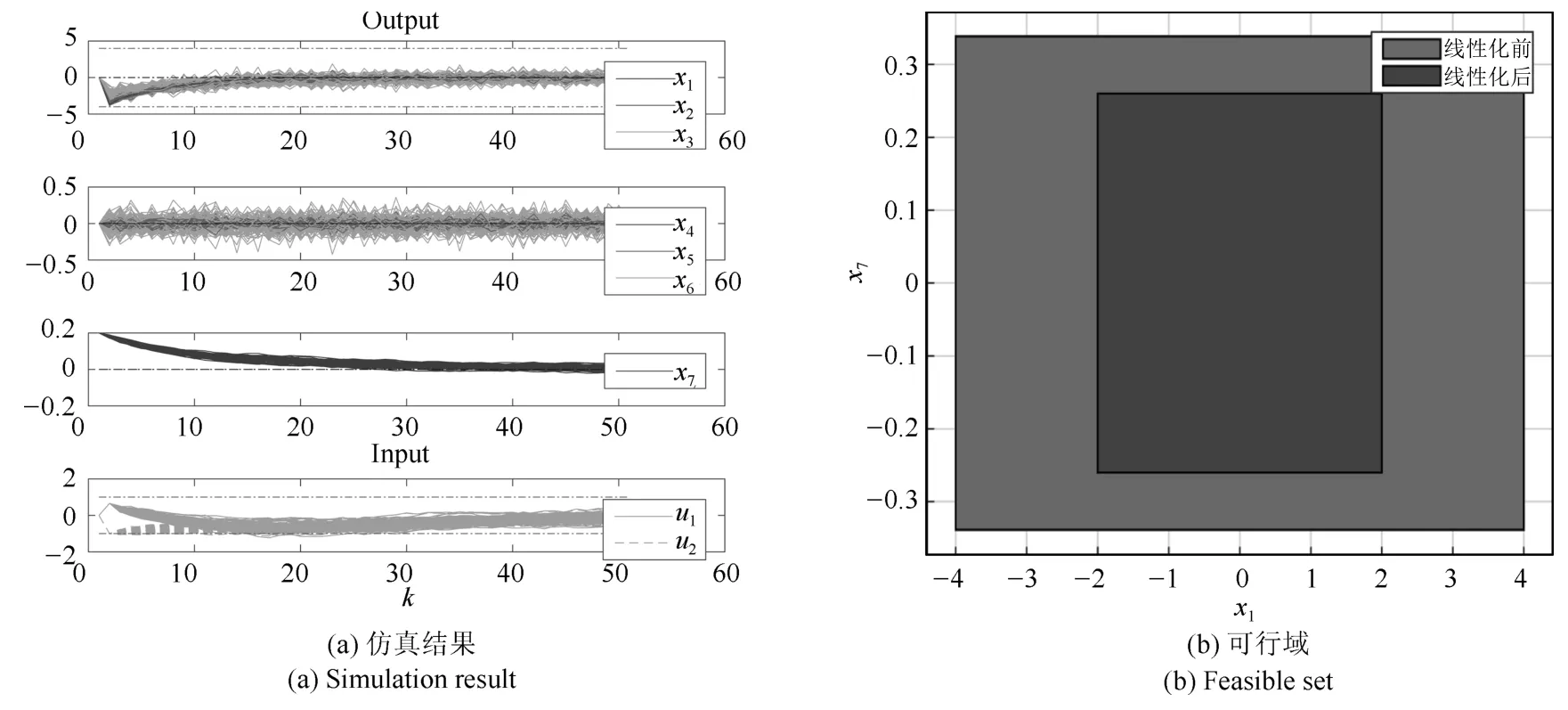
图14 基于CI的SMPC仿真结果Fig.14 Simulation result of CI-based SMPC

表7 RMPC和SMPC应用Table 7 Applications of RMPC and SMPC algorithms
4 总结与展望
本文回顾了RMPC和SMPC中主要的算法及各种算法的主要特点和运作方式.可以看到,所有的算法都是求解一个带约束的OCP问题以实现控制目标.递归可行性可以通过选择合适的终值约束来实现,而稳定性则一般是通过终值约束和终值惩罚共同作用或者是选择无穷预测时域来实现.对于有界干扰,RMPC和SMPC都能渐近收敛到RCI集.而对于无界噪声,正如Mayne在文献[32]中所指出,SMPC的稳定性要想被很好的解决,还有很长一段路要走.
事实上,保守性没有明确定义.但是可以从上述算法讨论看出,对于不确定系统,最终处理的约束往往是被紧缩过的,而保守性越大,指的就是约束紧缩程度越大,系统表现为距离约束边界越远.同时,保守性和算法可行域有着密切关系,往往保守性越大,可行域越小.
虽然近几十年来RMPC和SMPC得到了长足的发展,但在他们的实际应用中,仍有许多需要解决的问题.如系统规模变大时,求解不变集、LMI、紧缩约束等计算量是十分庞大的,当计算时间过长,系统状态与测量状态相差较远时,控制效果会很不理想,特别是对于快速动态系统,要求更快的运算速度.另外,在实际过程中如何确定噪声结构类型和取值范围、如何建立系统模型、如何设计保守性低的算法也将极大地影响控制效果.这些问题的可能解决办法和未来可能的研究方向如下:
观测器和控制器的综合:当系统状态不可测或只有部分可测时,利用观测器对状态进行观测来设计反馈控制器往往效果更好.有时为了实现一些特殊目的也需要获取某些新变量的信息,如为了实现无偏(Offset-free)跟踪需要将噪声看作新状态进行观测.观测器中的不同预测增益矩阵(滤波增益矩阵)L对控制器的影响也会显著不同,极端情况甚至会使得控制器不稳定.如何把L和反馈控制率进行综合设计,可否利用可测的部分状态信息来修正观测值,都是值得探索的话题.
前馈与反馈的综合:在经典控制论中,前馈的引入常常能有效地提高控制器的表现.而在模型预测当中,研究前馈的工作还相对较少,文献[137]讨论了这方面的内容,如何把前馈的设计和反馈结合起来,以及前馈在RMPC中的应用,特别是SMPC的应用仍需要更多的工作.
模型及优化问题的简化:简化模型和优化问题主要是为了提高运算速率,可以从模型降阶、模型转化、优化问题的分解方面考虑.模型降阶在传统MPC上的工作已经有不少,而在RMPC和SMPC方面仍有不足,特别是利用离线数据进行模型校准问题,仍是需要攻克的难点.利用基函数对原模型进行转化也是一个可研究的方向,如文献[138−139]等利用混沌多项式展开模型把高维系统模型转化为基函数的参数模型从而实现快速运算,类似的还有径向基函数模型.这些模型在RMPC和SMPC的相关研究还较少,例如现在对于基函数的选择往往是固定的,是否可以根据测量数据自适应地调整基函数,仍需要更多的研究.有时对优化问题进行分解,将线上计算部分和线下计算部分尽可能分离,或将复杂问题分解为可并行处理的子问题,往往可根据对象特性适当考虑.
轨迹跟踪问题:RMPC中的轨迹跟踪已有较多研究,SMPC领域相对较少,特别是对时变轨迹的跟踪问题.目前SMPC中对轨迹的跟踪往往是利用状态期望去跟踪轨迹,如果轨迹具有统计特性时(如上层计算传递下来的带有概率分布的轨迹),在惩罚函数中引入跟踪误差的期望和方差项,能否提高跟踪效果,如何解决其带来的计算问题,还需要更多的研究.另外,基于不变集的算法一般来说是不太适合跟踪轨迹的,因为系统状态最终都会收敛到不变集,如果跟踪轨迹不在不变集内,是否可设计不变集跟随轨迹变动的算法呢.前馈往往可以提供更多跟踪轨迹的信息,跟踪中引入前馈或许会有好的效果.
多领域的综合:文献[140−141]等对RMPC在经济MPC(EMPC)的应用进行了研究,而近期文献[142]将SMPC与EMPC进行了较好的综合,但这方面的研究相对来说是比较少的,仍有较多的工作可以进行.文献[143]最近提出了一种迭代MPC的算法,可对这种方法在RMPC和SMPC上的应用进行研究.
更多应用:从第3节的表7可以看到,RMPC和SMPC的应用是比较广泛的,但在医疗、金融、云计算、城市交通领域的应用相对较少,进一步加深对这些领域的研究,把理论和实际更紧密结合,探索RMPC和SMPC更多的适用场景,在促进各领域发展的同时也能促进RMPC和SMPC算法本身的研究进展.
附录
DME2M RMPC的“外部控制器”OCP:
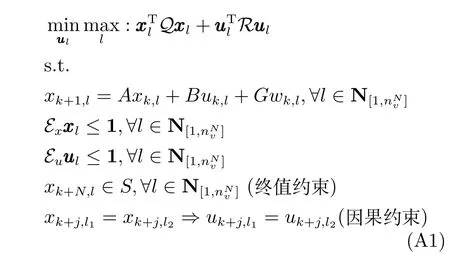
RT RMPC的OCP:

HT RMPC的OCP:

PT RMPC的OCP:


1 Kassmann D E,Badgwell T A,Hawkins R B.Robust steady-state target calculation for model predictive control.AIChE Journal,2000,46(5):1007−1024
2 Qin S J,Badgwell T A.A survey of industrial model predictive control technology.Control Engineering Practice,2003,11(7):733−764
3 Hrovat D,Di Cairano S,Tseng H E,Kolmanovsky I V.The development of model predictive control in automotive industry:a survey.In:Proceedings of the 2012 IEEE International Conference on Control Applications(CCA).Dubrovnik,Croatia:IEEE,2012.295−302
4 Xi Yu-Geng,Li De-Wei,Lin Shu.Model predictive controlstatus and challenges.Acta Automatica Sinica,2013,39(3):222−236(席裕庚,李德伟,林姝.模型预测控制–现状与挑战.自动化学报,2013,39(3):222−236)
5 MesbahA.Stochasticmodelpredictivecontrol:an overview and perspectives for future research.IEEE Control Systems,2016,366:30−44
6 Wang Y J,Rawlings J B.A new robust model predictive control method I:theory and computation.Journal of Process Control,2004,14(3):231−247
7 Mayne D Q.Model predictive control:recent developments and future promise.Automatica,2014,50(12):2967−2986
8 Campo P J,Morari M.Robust model predictive control.In:Proceedings of the 1987 American Control Conference.Minneapolis,MN,USA:IEEE,1987.1021−1026
9 Allwright J C,Papavasiliou G C.On linear programming and robust model-predictive control using impulseresponses.Systems&ControlLetters,1992,18(2):159−164
10 Zheng Z Q,Morari M.Robust stability of constrained model predictive control.In:Proceedings of the 1993 American Control Conference.San Francisco,California,USA:IEEE,1993.379−383
11 Lee J H,Yu Z H.Worst-case formulations of model predictive control for systems with bounded parameters.Automatica,1997,33(5):763−781
12 ScokaertPOM,MayneDQ.Min-maxfeedback model predictive control for constrained linear systems.IEEE Transactions on Automatic Control,1998,43(8):1136−1142
13 Blanchini F.Control synthesis for discrete time systems with control and state bounds in the presence of disturbances.Journal of Optimization Theory and Applications,1990,65(1):29−40
14 Gossner J R,Kouvaritakis B,Rossiter J A.Stable generalized predictive control with constraints and bounded disturbances.Automatica,1997,33(4):551−568
15 Lee Y I,Kouvaritakis B.Constrained receding horizon predictive control for systems with disturbances.International Journal of Control,1999,72(11):1027−1032
17 Limon D,Alvarado I,Alamo T,Camacho E F.Robust tube-based MPC for tracking of constrained linear systems with additive disturbances.Journal of Process Control,2010,20(3):248−260
18 Cannon M,Kouvaritakis B,Rakovic S V,Cheng Q F.Stochastic tubes in model predictive control with probabilistic constraints.IEEE Transactions on Automatic Control,2011,56(1):194−200
22 Farina M,Giulioni L,Magni L,Scattolini R.A probabilistic approach to model predictive control.In:Proceedings of the 52nd Annual Conference on Decision and Control(CDC).Florence,Italy:IEEE,2013.7734−7739
23 Farina M,Giulioni L,Magni L,Scattolini R.An approach to output-feedback MPC of stochastic linear discrete-time systems.Automatica,2015,55:140−149
24 Hokayem P,Chatterjee D,Lygeros J.On stochastic receding horizon control with bounded control inputs.In:Proceedings of the 48th IEEE Conference on Decision and Control,Held Jointly with the 28th Chinese Control Conference.Shanghai,China:IEEE,2009.6359−6364
25 Hokayem P,Chatterjee D,Ramponi F,Chaloulos G,Lygeros J.Stable stochastic receding horizon control of linear systems with bounded control inputs.In:Proceedings of the 19th International Symposium on Mathematical Theory of Networks and Systems.Budapest,Hungary:MTNS,2010.31−36
26 Primbs J A,Sung C H.Stochastic receding horizon control of constrained linear systems with state and control multiplicative noise.IEEE Transactions on Automatic Control,2009,54(2):221−230
27 Hokayem P,Cinquemani E,Chatterjee D,Ramponi F,Lygeros J.Stochastic receding horizon control with output feedback and bounded controls.Automatica,2012,48(1):77−88
28 Lucia S,Zometa P,Kgel M,Findeisen R.Efficient stochastic model predictive control based on polynomial chaos expansions for embedded applications.In:Proceedings of the 54th Annual Conference on Decision and Control(CDC).Osaka,Japan:IEEE,2015.3006−3012
29 Kouvaritakis B,Cannon M,RakoviS V,Cheng Q F.Explicit use of probabilistic distributions in linear predictive control.Automatica,2010,46(10):1719−1724
30 Kothare M V,Balakrishnan V,Morari M.Robust constrained model predictive control using linear matrix inequalities.Automatica,1996,32(10):1361−1379
31 Kouvaritakis B,Cannon M.Model Predictive Control:Classical,Robust and Stochastic.Switzerland:Springer,2015.
32 Mayne D.Robust and stochastic model predictive control:are we going in the right direction?Annual Reviews in Control,2016,41:184−192
33 Bemporad A,Morari M.Robust model predictive control:a survey,Robustness in Identi fication and Control.London:Springer,1999.207−226
35 Alamo T,Ramirez D R,de La Pea D M,Camacho E F.Min-max MPC using a tractable QP problem.Automatica,2007,43(4):693−700
36 Gao Y,Chong K T.The explicit constrained min-max model predictive control of a discrete-time linear system with uncertain disturbances.IEEE Transactions on Automatic Control,2012,57(9):2373−2378
38 Bertsekas D P.Nonlinear Programming(Second edition).Belmont,Massachusetts:Athena Scienti fic,1999
40 Wang Zhen-Ying.Constrained Robust Model Predictive Control of Discrete with Uncertaint Disturbance Case[Master dissertation],Harbin University of Science and Technology,China,2005.(王振英.不确定扰动情形下离散系统约束鲁棒模型预测控制[硕士学位论文],哈尔滨理工大学,中国,2005.)
41 Bemporad A.Reducing conservativeness in predictive control of constrained systems with disturbances.In:Proceedings of the 37th IEEE Conference on Decision and Control.Tampa,FL,USA:IEEE,1998,2:1384−1389
42 Goulart P J,Kerrigan E C,Maciejowski J M.Optimization over state feedback policies for robust control with constraints.Automatica,2006,42(4):523−533
43 Langson W,Chryssochoos I,RakoviS V,Mayne D Q.Robust model predictive control using tubes.Automatica,2004,40(1):125−133
44 Gautam A,Chu Y C,Soh Y C.Optimized dynamic policy for receding horizon control of linear time-varying systems with bounded disturbances.IEEE Transactions on Automatic Control,2012,57(4):973−988
46 Blanchini F.Survey paper:set invariance in control.Automatica,1999,35(11):1747−1767
47 Herceg M,Kvasnica M,Jones C N,Morari M.Multiparametric toolbox 3.0.In:Proceedings of the 2013 European Control Conference(ECC).Zurich,Switzerland:IEEE,2013.502−510
48 Mayne D Q,Rawlings J B,Rao C V,Scokaert P O M.Constrained model predictive control:stability and optimality.Automatica,2000,36(6):789−814
49 Goodwin G C,Kong H,Mirzaeva G,Seron M M.Robust model predictive control:re flections and opportunities.Journal of Control and Decision,2014,1(2):115−148
50 Zheng P Y,Li D W,Xi Y G,Zhang J.Improved model prediction and RMPC design for LPV systems with bounded parameter changes.Automatica,2013,49(12):3695−3699
51 Ping Xu-Bin,Ding Bao-Cang,Han Chong-Zhao.Dynamic output feedback robust model predictive control.Acta Automatica Sinica,2012,38(1):31−37(平续斌,丁宝苍,韩崇昭.动态输出反馈鲁棒模型预测控制.自动化学报,2012,38(1):31−37)
52 Cuzzola F A,Geromel J C,Morari M.An improved approach for constrained robust model predictive control.Automatica,2002,38(7):1183−1189
53 Kouvaritakis B,Rossiter J A,Schuurmans J.Efficient robust predictive control.IEEE Transactions on Automatic Control,2000,45(8):1545−1549
54 Mayne D Q,Langson W.Robustifying model predictive control of constrained linear systems.Electronics Letters,2001,37(23):1422−1423
55 Mayne D Q,Seron M M,RakoviS V.Robust model predictive control of constrained linear systems with bounded disturbances.Automatica,2005,41(2):219−224
57 Kolmanovsky I,Gilbert E G.Theory and computation of disturbance invariant sets for discrete-time linear systems.Mathematical Problems in Engineering,1998,4(4):317−367
58 Cala fiore G,Campi M C.Uncertain convex programs:randomized solutions and con fidence levels.Mathematical Programming,2005,102(1):25−46
59 Campi M C,Garatti S,Prandini M.The scenario approach for systems and control design.Annual Reviews in Control,2009,33(2):149−157
60 Schildbach G,Fagiano L,Frei C,Morari M.The scenario approach for stochastic model predictive control with bounds on closed-loop constraint violations.Automatica,2014,50(12):3009−3018
61 Cannon M,Cheng Q F,Kouvaritakis B,RakoviS V.Stochastic tube MPC with state estimation.Automatica,2012,48(3):536−541
62 Schwarm A T,Nikolaou M.Chance-constrained model predictive control.AIChE Journal,1999,45(8):1743−1752
63 Magni L,Pala D,Scattolini R.Stochastic model predictive control of constrained linear systems with additive uncertainty.In:Proceedings of the 2009 European Control Conference(ECC).Budapest,Hungary:IEEE,2009.2235−2240
64 Farina M,Scattolini R.Model predictive control of linear systems with multiplicative unbounded uncertainty and chance constraints.Automatica,2016,70:258−265
65 Farina M,Giulioni L,Scattolini R.Stochastic linear model predictive control with chance constraints–a review.Journal of Process Control,2016,44:53−67
66 Batina I.Model Predictive Control for Stochastic Systems By Randomized Algorithms[Ph.D.dissertation],Technische Universiteit Eindhoven,Netherlands,2004.
67 Blackmore L,Ono M,Bektassov A,Williams B C.A probabilistic particle-control approximation of chanceconstrained stochastic predictive control.IEEE Transactions on Robotics,2010,26(3):502−517
68 Campi M C,Garatti S.The exact feasibility of randomized solutions of uncertain convex programs.SIAM Journal on Optimization,2008,19(3):1211−1230
69 Campi M C,Garatti S.A sampling-and-discarding approach to chance-constrained optimization:feasibility and optimality.Journal of Optimization Theory and Applications,2011,148(2):257−280
70 Cala fiore G C,Campi M C.The scenario approach to robust control design.IEEE Transactions on Automatic Control,2006,51(5):742−753
71 Cala fiore G C.Random convex programs.SIAM Journal on Optimization,2010,20(6):3427−3464
72 Alamo T,Tempo R,Luque A,Ramirez D R.Randomized methods for design of uncertain systems:sample complexity and sequential algorithms.Automatica,2015,52:160−172
73 Cannon M,Kouvaritakis B,Wu X J.Probabilistic constrained MPC for multiplicative and additive stochastic uncertainty.IEEE Transactions on Automatic Control,2009,54(7):1626−1632
74 Gidon D,Graves D B,Mesbah A.Model predictive control of thermal effects of an atmospheric pressure plasma jet for biomedical applications.In:Proceedings of the 2016 American Control Conference(ACC).Boston,MA,USA:IEEE,2016.4889−4894
75 Wang Qiu,Qu Ting,Chen Hong.Steering control of autonomous vehicles based on stochastic model predictive control.Information and Control,2015,44(4):499−506(王秋,曲婷,陈虹.基于随机模型预测控制的自主车辆转向控制.信息与控制,2015,44(4):499−506)
76 Carvalho A,Gao Y Q,Lefevre S,Borrelli F.Stochastic predictive control of autonomous vehicles in uncertain environments.In:Proceedings of the 12th International Symposium on Advanced Vehicle Control.Tuat,Japan:AVEC,2014.
77 Schildbach G,Borrelli F.Scenario model predictive control for lane change assistance on highways.In:Proceedings of the 2015 IEEE Intelligent Vehicles Symposium(IV).Seoul,Korea:IEEE,2015.611−616
78 Moser D,Waschl H,Kirchsteiger H,Schmied R,del Re L.Cooperative adaptive cruise control applying stochastic linear model predictive control strategies.In:Proceedings of the 2015 European Control Conference(ECC).Linz,Austria:IEEE,2015.3383−3388
79 Liu C C,Carvalho A,Schildbach G,Hedrick J K.Stochastic predictive control for lane keeping assistance systems using a linear time-varying model.In:Proceedings of the 2015 American Control Conference(ACC).Chicago,IL,USA:ACC,2015.3355−3360
80 Gray A,Gao Y Q,Lin T,Hedrick J K,Borrelli F.Stochastic predictive control for semi-autonomous vehicles with an uncertain driver model.In:Proceedings of the 16th International IEEE Annual Conference on Intelligent Transportation Systems-(ITSC).The Hague,the Netherlands:IEEE,2013.2329−2334
81 Carvalho A,Lefvre S,Schildbach G,Kong J,Borrelli F.Automated driving:the role of forecasts and uncertaintya control perspective.European Journal of Control,2015,24:14−32
82 Qu Ting.Driver Behavior Modeling Based on Stochastic Model Predictive Control[Ph.D.dissertation],Jilin University,China,2015.(曲婷.基于随机模型预测控制的驾驶员行为建模[博士学位论文],吉林大学,中国,2015.)
83 Kayacan E,Ramon H,Saeys W.Robust trajectory tracking error model-based predictive control for unmanned ground vehicles.IEEE/ASME Transactions on Mechatronics,2016,21(2):806−814
84 Zhu X Y,Zhang H,Cao D P,Fang Z D.Robust control of integrated motor-transmission powertrain system over controller area network for automotive applications.Mechanical Systems and Signal Processing,2015,58−59:15−28
85 Gao Y Q,Gray A,Tseng H E,Borrelli F.A tube-based robust nonlinear predictive control approach to semiautonomous ground vehicles.Vehicle System Dynamics,2014,52(6):802−823
86 Zhang X J,Grammatico S,Schildbach G,Goulart P,Lygeros J.On the sample size of randomized MPC for chance-constrained systems with application to building climate control.In:Proceedings of the 2014 European Control Conference(ECC).Strasbourg,France:IEEE,2014.478−483
87 Yao J.Determining the energy performance of manually controlled solar shades:a stochastic model based cosimulation analysis.Applied Energy,2014,127:64−80
88 Tanner R A,Henze G P.Stochastic control optimization for a mixed mode building considering occupant window opening behaviour.Journal of Building Performance Simulation,2014,7(6):427−444
89 Ma Y D,Matuško J,Borrelli F.Stochastic model predictive control for building HVAC systems:complexity and conservatism.IEEE Transactions on Control Systems Technology,2015,23(1):101−116
90 Xu X H,Wang S W,Huang G S.Robust MPC for temperature control of air-conditioning systems concerning on constraints and multitype uncertainties.Building Services Engineering Research and Technology,2010,31(1):39−55
91 Yang Shi-Zhong,Ren Qing-Chang.Robust model predictive control for variable air volume air conditioning system.Computer Engineering and Applications,2013,49(6):8−11,104(杨世忠,任庆昌.鲁棒模型预测控制在变风量空调系统中的应用.计算机工程与应用,2013,49(6):8−11,104)
92 Ren M F,Zhang J H,Jiang M,Yu M,Xu J L.Minimum(h,φ)entropy control for non-Gaussian stochastic networked control systems and its application to a networked dc motor control system.IEEE Transactions on Control Systems Technology,2015,23(1):406−411
93 Preindl M.Robust control invariant sets and Lyapunovbased mpc for ipm synchronous motor drives.IEEE Transactions on Industrial Electronics,2016,63(6):3925−3933
94 Zhao X D,Zhang L X,Shi P,Karimi H R.Robust control of continuous-time systems with state-dependent uncertainties and its application to electronic circuits.IEEE Transactions on Industrial Electronics,2014,61(8):4161−4170
95 Rhouma A,Bouani F.Robust model predictive control of uncertain fractional systems:a thermal application.IET Control Theory&Applications,2014,8(17):1986−1994
96 Shahsavari B,Maasoumy M,Sangiovanni-Vincentelli A,Horowitz R.Stochastic model predictive control design for load management system of aircraft electrical power distribution.In:Proceedings of the 2015 American Control Conference(ACC).Chicago,IL,USA:IEEE,2015.3649−3655
97 Hajiloo A,Xie W F.The stochastic robust model predictive control of shimmy vibration in aircraft landing gears.Asian Journal of Control,2015,17(2):476−485
98 Marantos P,Bechlioulis C P,Kyriakopoulos K J.Robust trajectory tracking controlfor small-scale unmanned helicopters with model uncertainties.IEEE TransactionsonControlSystemsTechnology,2017,doi:10.1109/TCST.2016.2642160
99 Alexis K,Papachristos C,Siegwart R,Tzes A.Robust model predictive flight control of unmanned rotorcrafts.Journal of Intelligent&Robotic Systems,2016,81(3−4):443−469
100 Zhang Shao-Kang.Research on Robust Model Predictive Control Based on LPV Model for Hypersonic Vehicles[Master dissertation],Tianjin University,China,2014.(张少康.基于LPV模型的高超声速飞行器鲁棒预测控制方法研究[硕士学位论文],天津大学,中国,2014.)
101 Blackmore L,Ono M,Williams B C.Chance-constrained optimal path planning with obstacles.IEEE Transactions on Robotics,2011,27(6):1080−1094
102 GonzálezR,FiacchiniM,GuzmánJL,ÁlamoT,Rodrguez F.Robust tube-based predictive control for mobile robots in off-road conditions.Robotics and Autonomous Systems,2011,59(10):711−726
103 Goodwin G C,Medioli A M.Scenario-based,closed-loop model predictive control with application to emergency vehicle scheduling.International Journal of Control,2013,86(8):1338−1348
104 Jurado I,Maestre J M,Velarde P,Ocampo-Martinez C,Fernandez I,Tejera B I,del Prado J R.Stock management in hospital pharmacy using chance-constrained model predictive control.Computers in Biology and Medicine,2016,72:248−255
105 Chang H,Krieger A,Astol fiA,Pistikopoulos E N.Robust multi-parametric model predictive control for LPV systems with application to anaesthesia.Journal of Process Control,2014,24(10):1538−1547
106 Jurado I,Millán P,Quevedo D,Rubio F R.Stochastic MPC with applications to process control.International Journal of Control,2015,88(4):792−800
107 Tang Y,Peng C,Yin S,Qiu J B,Gao H J,Kaynak O.Robust model predictive control under saturations and packet dropouts with application to networked flotation processes.IEEE Transactions on Automation Science and Engineering,2014,11(4):1056−1064
108 Bakošová M,Oravec J.Robust model predictive control for heat exchanger network.Applied Thermal Engineering,2014,73(1):924−930
109 Ghaffari V,Naghavi S V,Safavi A A.Robust model predictive control of a class of uncertain nonlinear systems with application to typical CSTR problems.Journal of Process Control,2013,23(4):493−499
110 Liu Zheng-Feng,Wang Jing-Cheng,Shi Yuan-Hao,Zhang Lang-Wen.Robust distributed model prediction control for coal- fired power plant boiler combustion system.In:Proceedings of the 25th Chinese Process Control Conference.Dalian,China,2014.6(刘正峰,王景成,史元浩,张浪文.燃煤电站锅炉燃烧系统的鲁棒分布式模型预测控制.见:第25届中国过程控制会议.大连,中国:中国自动化学会过程控制专业委员会,2014.6)
111 Yorgashov Yu A.Robust model predictive control of industrial reactive distillation column.Journal of Shenyang University of Chemical Technology,2009,23(1):92−96
112 Yang Bin-Hu,Yang Wei-Dong,Qu Lei.Robust predictivemodel-control strategy for automatic gauge control in hot strip finishing milling.Control Theory&Applications,2011,28(6):799−804(杨斌虎,杨卫东,曲蕾.热轧带钢自动厚度控制鲁棒预测模型与控制策略.控制理论与应用,2011,28(6):799−804)
113 Cominesi S R,Farina M,Giulioni L,Picasso B,Scattolini R.Two-layer predictive control of a micro-grid including stochastic energy sources.In:Proceedings of the 2015 American Control Conference(ACC).Chicago,IL,USA:IEEE,2015.918−923
114 Hans C A,Sopasakis P,Bemporad A,Raisch J,Reincke-Collon C.Scenario-based model predictive operation control of islanded microgrids.In:Proceedings of the 54th Annual Conference on Decision and Control(CDC).Osaka,Japan:IEEE,2015.3272−3277
115 Zhu D H,Hug G.Decomposed stochastic model predictive control for optimal dispatch of storage and generation.IEEE Transactions on Smart Grid,2014,5(4):2044−2053
116 Patrinos P,Trimboli S,Bemporad A.Stochastic MPC for real-time market-based optimal power dispatch.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference(CDC-ECC).Orlando,FL,USA:IEEE,2011.7111−7116
117 Zhang Yan,Zhang Tao,Liu Ya-Jie,Guo Bo.Stochastic model predictive control for energy management optimization of an energy local network.Proceedings of the CSEE,2016,36(13):3451−3462(张彦,张涛,刘亚杰,郭波.基于随机模型预测控制的能源局域网优化调度研究.中国电机工程学报,2016,36(13):3451−3462)
118 Velarde P,Maestre J M,Ocampo-Martinez C,Bordons C.Application of robust model predictive control to a renewable hydrogen-based microgrid.In:Proceedings of the 15th European Control Conference(ECC).Aalborg,Denmark:ECC,2016.1209−1214
119 Riverso S,Mancini S,Sarzo F,Ferrari-Trecate G.Model predictive controllers for reduction of mechanical fatigue in wind farms.IEEE Transactions on Control Systems Technology,2017,25(2):535−549
120 Kou P,Gao F,Guan X H.Stochastic predictive control of battery energy storage for wind farm dispatching:using probabilistic wind power forecasts.Renewable Energy,2015,80:286−300
121 Hu Jing.Research on application of stochastic model predictive control in wind power generation systems[Master dissertation],North China Electric Power University,China,2015.(胡婧.随机模型预测控制在风力发电系统的应用[硕士学位论文],华北电力大学,中国,2015.)
122 Evans M A,Cannon M,Kouvaritakis B.Robust MPC tower damping for variable speed wind turbines.IEEE Transactions on Control Systems Technology,2015,23(1):290−296
123 Mirzaei M,Poulsen N K,Niemann H H.Robust model predictive control of a wind turbine.In:Proceedings of the 2012 American Control Conference(ACC).Montral,Canada:IEEE,2012.4393−4398
124 Grosso J M,Ocampo-Martnez C,Puig V,Joseph B.Chance-constrained model predictive control for drinking water networks.Journal of Process Control,2014,24(5):504−516
125 Huang Chong-Yin,Luo Can,Zhao Yong,Han Shou-Dong.Application of stochastic predictive control model to sustainable utilization of water resources.Water Resources and Power,2011,29(12):16−20(黄翀胤,罗灿,赵勇,韩守东.随机预测控制模型及其在水资源可持续中的应用.水电能源科学,2011,29(12):16−20)
127 Di Cairano S,Bernardini D,Bemporad A,Kolmanovsky I V.Stochastic MPC with learning for driver-predictive vehicle control and its application to HEV energy management.IEEE Transactions on Control Systems Technology,2014,22(3):1018−1031
128 Tettamanti T,Luspay T,Kulcsár B,Pni T,Varga I.Robust control for urban road traffic networks.IEEE Transactions on Intelligent Transportation Systems,2014,15(1):385−398
129 Li S K,De Schutter B,Yang L X,Gao Z Y.Robust model predictive control for train regulation in underground railway transportation.IEEE Transactions on Control Systems Technology,2016,24(3):1075−1083
130 Bemporad A,Bellucci L,Gabbriellini T.Dynamic option hedging via stochastic model predictive control based on scenario simulation.Quantitative Finance,2014,14(10):1739−1751
131 Zhang Wei-Guo,Du Qian.Dynamic hedging european option based on stochastic model predictive controldynamic hedging European option based on stochastic model predictive control.Journal of South China University of Technology(Social Science Edition),2016,18(4):1−9(张卫国,杜谦.基于随机模型预测控制的欧式期权动态对冲研究.华南理工大学学报(社会科学版),2016,18(4):1−9)
132 Schildbach G,Morari M.Scenario-based model predictive control for multi-echelon supply chain management.European Journal of Operational Research,2016,252(2):540−549
133 Rostampour V,Keviczky T.Robust randomized model predictive control for energy balance in smart thermal grids.In:Proceedings of the 2016 European Control Conference(ECC).Aalborg,Denmark:IEEE,2016.1201−1208
134 Ghanbari H,Litoiu M,Pawluk P,Barna C.Replica placement in cloud through simple stochastic model predictive control.In:Proceedings of the 2014 IEEE 7th International Conference on Cloud Computing(CLOUD).Anchorage,AK,USA:IEEE,2014.80−87
135 Pizzonia F,Castiglione T,Bova S.A Robust Model Predictive Control for efficient thermal management of internal combustion engines.Applied Energy,2016,169:555−566
136 Hajiloo A,Keshmiri M,Xie W F,Wang T T.Robust online model predictive control for a constrained image-based visual servoing.IEEE Transactions on Industrial Electronics,2016,63(4):2242−2250
137 Carrasco D S,Goodwin G C.Feedforward model predictive control.Annual Reviews in Control,2011,35(2):199−206
138 Paulson J A,Mesbah A,Streif S,Findeisen R,Braatz R D.Fast stochastic model predictive control of highdimensional systems.In:Proceedings of the 53rd Conference on Decision and Control.Los Angeles,California,USA:IEEE,2014.2802−2809
139 Terejanu G,Singla P,Singh T,Scott P D.Approximate interval method for epistemic uncertainty propagation using polynomial chaos and evidence theory.In:Proceedings of the 2010 American Control Conference.Baltimore,MD,USA:IEEE,2010.349−354
140 Bayer F A,Mller M A,Allgwer F.Tube-based robust economic model predictive control.Journal of Process Control,2014,24(8):1237−1246
141 Hovgaard T G,Larsen L F S,Jorgensen J B.Robust economic MPC for a power management scenario with uncertainties.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference(CDC-ECC).Orlando,FL,USA:IEEE,2011.1515−1520
142 Bayer F A,Lorenzen M,Mller M A,Allgwer F.Robust economic model predictive control using stochastic information.Automatica,2016,74:151−161
143 Feller C,Ebenbauer C.A stabilizing iteration scheme for model predictive control based on relaxed barrier functions.Automatica,2017,80:328−339
