批次过程控制—回顾与展望
2017-03-10卢静宜曹志兴高福荣
卢静宜 曹志兴 高福荣
在传统流程工业中,炼油、炼钢、造纸等大规模生产过程占据着主导地位.这类过程从原料输入到制品输出是连续不间断的,被称为连续过程(Continuous process)[1].随着经济的发展,产品种类增多,市场需求变化加快.为了迎合这些需求,对于具有高附加值的产品,小规模多工序的生产方式更受到人们的青睐.这类过程将原料按加工顺序转化为产品,并通过重复操作获得更多同种产品.这类过程被称为批次过程(Batch process),也叫作间歇过程.目前已经被广泛应用于食品、化工、制药、塑料加工等行业中[2−3].
在流程工业中,生产效率和产品品质很大程度上由过程控制的精度决定.在过去的五十年中,过程控制理论及其应用都取得了深远的发展.但传统的过程控制理论和算法大多针对连续过程提出,而批次过程有很多不同于连续过程的特性.这些特性使得传统的控制方法不适用于批次过程或难以取得理想的控制精度.
本文从批次过程的本质特性出发,总结了批次过程区别于连续过程的“多重时变”特性,指出了研究批次过程算法的必要性.进而,基于这些特性,我们对批次过程控制算法近30年的发展进行回顾和分析.我们把批次过程控制算法的发展分为三个阶段:连续控制算法阶段、迭代学习控制阶段和二维控制算法阶段,并在此基础上,进一步介绍了批次过程在控制、优化与建模层面上可能的发展方向.
1 批次过程的“多重时变”特性
批次过程区别于连续过程的特性可以用“多重时变”来概括,如图1所示.即“多样产品”、“重复运行”、“时段切换”和“变换指标”.“多样产品”指在同一个过程装备上可生产不同种类的产品;“重复运行”指通过重复相同的操作以获得多件产品;“时段切换”指在一个批次内生产过程需分时段地在不同的操作条件间切换;“变换指标”指系统控制的指标随时段变换.以在塑料成型加工领域占有重要地位的注塑过程[4](Injection molding process)为例,我们来进一步阐释批次过程的“多重时变”特性:1)多:在注塑过程中,通过变更填充的材料以及模具,同一台注塑机可用来生产不同材质、形状和大小的多种产品;2)重:注塑机通过不断地重复注射、保压、冷却等操作来加工多件塑料制品;3)时:一个典型的注塑过程由注射、保压和冷却三个时段组成.注塑机在不同的时段运行不同的操作.在注射阶段,螺杆以一定的速度将高分子材料填充入模具;而在保压阶段则是在保证模腔压力一定的条件下进行额外的填充来抵消冷却引起的材料收缩.4)变:在注塑过程的不同的生产阶段,决定产品质量的关键变量不同,我们关注的指标量也有所变化.在注射阶段,注射速度最为关键,它对塑料制品的机械强度,如抗拉强度、冲击强度等都有直接影响.而在保压阶段,模腔压力对产品的尺寸、稳定性及表面光滑性影响最大.因而,在注塑阶段的被控变量是注射速度,而在保压阶段的被控变量则是模腔压力.

图1 批次过程多重时变特性示意图Fig.1 Illustration of the characteristics of batch processes
“多重时变”特性是多数批次过程所共有的.在很多典型的批次过程中,如间歇发酵过程、半导体加工等,我们都可以找到这些特性.“多重时变”特性也是批次过程能够提高生产效率和灵活性的关键.正是由于这些特性,批次过程可以很快地适应客户对于产品种类、性质和数量上的需求变化,适应市场的多样性与多变性,从而更符合定制化的生产模式.但这些特性为控制算法的设计带来了挑战.
从控制的角度来看,批次过程“多”、“时”、“变”的特性引起两方面的变化:一是被控对象本身的动态特性变化;二是控制器的设定值的变化.在一个批次中,控制器的设定值通常不是一个固定值,而是根据具体生产状况和用户需求优化得来的曲线.设定值的变化使得系统表现出明显的时变特性.总体来说,“多时变”特性使得系统动态特性变化范围大且频繁,非线性特征显著,而批次过程通常要求快速投运,没有足够的时间运行大量的实验以重新建模.这直接导致精确的系统模型难以获得,显著的模型失配难以避免,进而导致适用于连续过程的多种基于模型的控制算法不适用于批次过程.与此同时,高精度的控制要求也使得多数针对具有模型偏差的系统的鲁棒控制算法显得太过保守,不能够在短时间内实现目标跟踪.因而,过程特性与控制性能的要求构成的矛盾给控制算法的设计带来了巨大的挑战.
另一方面,批次过程的重复特性给控制算法的设计带来了转机.基于重复特性,研究者们引入了学习控制算法.这种算法允许控制效果在控制的初期表现相对较差,但利用在线学习使控制性能沿批次方向逐步改善,从而逐渐达到控制要求.学习算法的引入降低了控制算法对模型的依赖,简化算法的设计,使得批次过程控制得到了进一步的发展和更广泛的应用.接下来我们将系统回顾批次过程控制算法的发展.
2 批次过程发展回顾
2.1 连续过程控制阶段
批次过程控制算法的出现晚于连续过程.在批次过程控制发展的初期,很多针对连续过程的控制算法已经十分成熟,如模型预测控制[5−11]、鲁棒控制[12−14]、自适应控制[15−16]等.因而人们通常把批次过程当作有限时长的特殊的连续过程,进而将连续过程的控制算法直接应用在批次过程中.
早期,研究人员们尝试利用在连续过程中广泛应用的PID控制器来控制批次过程.文献[17]应用一个简单的PI控制器控制注塑过程中的注射速度.实验表明,当控制器的设定值发生变化时,系统输出有明显震荡.PI控制器很难得到令人满意的跟踪效果.这种现象是由系统的时变特性所造成.
为了更好地处理系统的时变特性,文献[17]应用自适应算法来控制注射速度.这种算法通过在线测量得到的输入输出数据来估计出系统模型,再利用得到的模型配置闭环系统的零极点,如图2所示.文献[18]用一个GPC控制器替代[17]中的零极点配置控制器,从而克服了控制器对模型结构失配敏感的问题.总体来说,这类自适应控制算法通过在线更新模型得到一个时变的模型.该时变模型更好地表征了系统的时变特性,从而一定程度上解决了模型不准确的问题.相比于简单的PI、PID控制器,自适应算法明显改善了控制效果.但由于模型辨识算法的收敛需要足够的数据量,所以在每个批次的初始阶段以及设定值发生改变的初期,系统输出的震荡依然明显,需要的稳定时间仍然较长.

图2 自适应控制器示意图Fig.2 Control scheme of adaptive control
文献[19−20]从不同角度出发,尝试在过程开始前建立较准确的机理模型.作者对间歇反应器进行机理建模,得到一个非线性模型,基于该模型设计非线性模型预测控制算法(Nonlinear model predictive control).文献[21−22]考虑到准确的机理模型难以建立,而应用神经网络等基于数据的方式进行建模.这类方法主要面临着两方面的挑战:1)建模困难:很多批次过程机理复杂,人们对机理本身的了解有限,更难说建模.而基于数据的建模则需要大量实验.当产品配方变化时,需要重新进行大量实验来更新模型.在批次过程中产品更换频繁,且通常要求生产过程可以即时投运.这些要求令基于实验数据的准确建模不具有可行性.2)计算困难:基于这类模型的控制算法通常需要在线求解非线性优化问题,这对于硬件系统的计算能力是个不小的挑战.
从上述回顾可以看出,在这一阶段,研究者们在应用连续过程控制思想设计批次过程控制算法方面做了大量尝试,从简单的PID控制器,到自适应控制器和非线性控制器.这些尝试奠定了批次过程控制算法的发展基础,但这些方法没能突破“多时变”特性给控制算法设计带来的困境,针对时变系统的控制效果依然不够令人满意.同时这些设计较为繁琐,不够简明,对模型的准确性依赖性大.因而,在批次过程研究的第二阶段,研究者们跳出连续过程控制的框架,着眼于批次过程的重复特性,并利用重复特性设计不同于连续过程的学习控制算法.
2.2 迭代学习控制阶段
迭代学习控制(Iterative learning control,ILC)[23−24]是一种基于过程重复特性的控制算法.这种算法的基本思想是利用以前批次的跟踪误差来修正当前批次的系统输入.通过引入学习的思想,来降低控制算法对模型准确性的依赖.
为了更好地展示批次过程有限时长特性和重复特性,我们通常用两个维度来描述批次过程,即时间维度(Time dimension,表示为t)和批次维度(Batch dimension,表示为k).批次过程的时变特性通常体现在时间维度上.批次维度上则体现了明显的重复特性.基于批次过程的二维表示,基本的迭代学习控制律可以表示为

此处,u表示系统输入,e表示对设定值的跟踪误差.式(1)所示控制律与PID中的比例控制器有相似结构,因而被称为P类迭代学习控制算法(P-type ILC)[25].随后,为了提高收敛速度和算法的鲁棒性,研究者们进一步提出了D-type[25]、PI-type[26]、PID-type[27]等算法,以及利用多批次输入输出信息的高阶迭代学习控制算法(High-order ILC)[28].
这类算法可视为单纯的数据驱动算法[29−30],控制律的设计不依赖于系统模型.另一种能够将模型信息与历史数据结合的模最优迭代学习控制算法(Norm optimal ILC)[31−33]在批次过程控制中有着更广泛的应用.如文献[31]所示,假定批次过程时长为N,它的时变线性近似模型可表示为:

最优迭代学习控制利用批次过程有限时长的特点,将整个批次的系统输入与输出分别集结成两个长向量:


这里


直观上来看,问题式(8)中的等式约束为对当前批次输出的预测.该预测值由两部分组成,一部分是G(k),可理解为基于模型的预测;另一部分为(k−1)−G(k−1),是利用前一批次的数据对当前模型预测得到输出的校正.对比该式与式(6)可发现,校正部分的引入可消除重复的模型误差和外部扰动对系统的影响,从而降低算法对准确的模型的依赖.
从数学角度来看,我们把跟踪误差表示为:
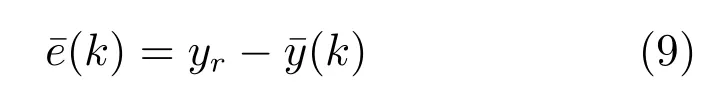
在不考虑约束的情况下,式(8)存在解析解:

将式(10)与式(1)对比可发现,相比于式(1)中点对点的学习,式(10)融入了批次所有时刻的跟踪误差信息.因而,这类算法可以显著地提高收敛速度.文献[34−35]进一步研究了如何合理地设计优化问题,使得跟踪误差单调减小.
基于这个框架,研究者们进一步做了两方面的工作:1)进一步增强算法的鲁棒稳定性.文献[36]针对初始状态不确定和存在干扰的系统提出了一种鲁棒迭代学习算法.文中给出了系统稳定的充分必要条件,并将该方法应用于注塑机注射速度的控制当中.实验结果表明控制效果可以随批次的增加不断地改善.文献[37]基于线性矩阵不等式针对不确定性系统提出了一种鲁棒迭代学习算法.2)提高模型G的准确性.文献[38]利用在线测量得到的数据来估计和更新模型G,从而降低算法对于模型的依赖性,并进一步提高控制效果.文献[39−41]提出用神经网络和神经模糊模型(Neuro-fuzzy model[42])来代替式(6)中的线性模型G.从时间方向上来看,单一的迭代学习控制可以理解为前馈控制.由式(1)及式(10)不难看出,k批次t时刻的输入u(t,k)只跟前一批次的系统输入u(t,k−1)及跟踪误差有关,而与当前批次的其他时间点的输入输出信号无关.因而迭代学习控制律在批次方向具有反馈作用,但在时间方向上未形成闭环.时间方向反馈作用的缺失意味着系统对抗非重复扰动的能力较弱.当系统中存在不重复干扰时,系统收敛性难以保证.为了解决这一问题,研究人员们提出将迭代学习控制算法与批次内的反馈控制算法结合(如图3所示),以此来提高系统的稳定性和收敛速度.
迭代学习控制与模型预测控制(Model predictive control)的结合是反馈迭代学习控制中的一类重要方法,也是在批次过程中应用得较为广泛的一类方法.文献[43]在最优迭代学习控制的框架下引入反馈机制:首先通过求解问题(8)得到迭代学习控制对应的输入¯u(k),在此基础上,利用卡尔曼滤波(Kalman filter)综合当前已经获得的输入输出信息,估计出当前时刻的跟踪误差,并利用该估计值进一步修正¯u(k),进而得到真正的系统输入.简单来说,在每个批次内的每个时间点上,这种方法利用当前信息来校正迭代学习控制算法得到的系统输出,从而引入时间方向的反馈作用.文献[44]将该方法应用于间歇反应器的控制,实验结果表明,该方法在跟踪效果和收敛速度上优于单纯的迭代学习控制.此后,作者将这一设计思路应用在模拟移动床色谱系统(Simulated moving bed chromatography)的控制中[45],同样取得较好的控制效果.在文献[46]中,作者进一步从理论上分析了该类方法的收敛性.

图3 反馈迭代学习控制示意图Fig.3 Control scheme of feedback iterative learning control
此外,研究者们还提出了很多其他方式将迭代学习控制与反馈控制相结合.文献[47]在文献[43]的基础上,提出了一种两阶段(Two-stage)的结合方式,来降低算法对不重复干扰的敏感性.在文献[48]中,作者将内模控制(Internal model control)与迭代学习相结合.此外,间接迭代学习控制方法(Indirect iterative learning control)[49−53]也是一类重要的结合方式.这类方法先设计一个反馈控制器,然后利用迭代学习控制策略来调节反馈控制器的设定值,以达到沿批次方向改善跟踪性能的目的.
2.3 二维系统控制阶段
在批次过程控制发展的第三阶段,人们提出利用二维控制理论来分析设计反馈迭代学习控制方法.二维系统理论[54−55]的研究起始于20世纪70年代,目前已经十分完备.如前所述,批次过程有时间和批次两个维度.从本质上来说,它是一个二维系统.而完善的二维系统理论可以简化反馈迭代学习控制的分析和设计.
文献[56]首次利用二维系统理论来分析基本的P类迭代学习控制的设计.在二维理论框架下研究了如何选取式(1)中的增益K来保证系统的稳定性.文献[57]首先提出在二维理论框架下设计带有反馈控制的迭代学习控制,并应用于批次过程控制中.在文中,作者定义

同时给定控制器结构为

不难看出,式 (11)在式(1)的基础上引入了状态反馈控制器K1∆kx(t,k)和跟踪误差补偿器K2(t,k).该文献的重点是如何利用二维系统理论来选择合适的控制器参数(K1,K2,L)来保证闭环系统的稳定性.先定义系统增广状态:

如式(12)所示,利用这两个增广状态将闭环系统方程写成2D-Roesser模型.

为了分析系统(14)的稳定性,作者设计了一组二维李雅普诺夫函数(Lyapunov function):

继而提出当式(11)中的K1、K2、L使得V、Vh、Vv满足时,系统具有二维稳定性,即具有时间和批次两个方向上的稳定性.

文献[57]首次提出了批次过程控制算法需要同时保证二维稳定性,同时给出了一种在二维系统理论框架下设计反馈迭代学习控制的通用方法和思路.基于这一思路,我们可以针对批次过程中模型失配、非重复干扰,非重复初始状态、时滞等问题设计出相应的控制策略.文献[58]中给出了针对状态延时和系统时变特性的鲁棒控制策略;文献[59−60]设计了一种基于二维系统的线性最优控制(Linear optimal control),通过求解优化问题来提高收敛速度.文献[61]针对系统的不确定扰动和初始状态,基于二维Fornasini-Marchsini(FM)模型提出了一种鲁棒控制算法.文献[62−65]针对执行器故障和传感器故障分别给出了二维容错控制算法.文献[66]将这种容错控制的思想推广到网络系统.文献[67−68]则针对带有时滞的批次过程提出了一系列鲁棒控制算法.
二维框架下迭代学习控制与模型预测控制的结合也是一类重要算法.文献[69]提出了一种迭代学习预测控制.这种方法的设计思路非常直观.首先,对系统建立一个受控自回归整合滑动平均模型(Controlled auto-regressive integrated moving average model),表示为:
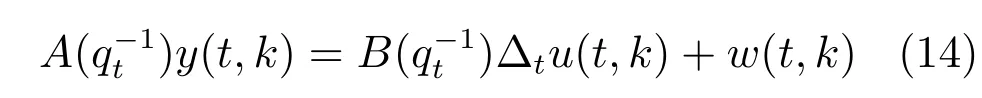
设定控制器的结构为:

将式(15)代入式(14)可得到一个二维等价模型(2D equivalent model):

通过求解二次规划问题(16)来求取r(t,k)

式(16)中的预测模型在时间方向进行了多步预测而批次方向只做一步预测.文献[69]还给出了批次方向多步预测的算法,并验证了批次方向的多步预测可进一步提高收敛速度.
文献[44]与文献[69]中的方法都是将模型预测控制与迭代学习控制相结合.与文献[44]中的两步求解不同,文献[69]直接基于二维系统做一步优化即可得到控制律,这使得控制器的设计更为简单灵活.基于文献[69]所提出的框架,文献[70]给出了该类方法在注射速度控制问题上的实验结果,证明了该方法的有效性.文献[71]利用一个多目标优化问题来解决双注塑机的控制问题.文献[72]将该方法推广到多阶段(Multi-phase)的批次过程控制.文献[73]设计了一种两步优化方法来降低该类方法对不重复性干扰的敏感性.文献[73]将式(13)中的不等式引入优化问题中,作为优化问题的约束条件,从而利用二维李雅普诺夫函数保证系统鲁棒稳定性.文献[74−75]分别将该方法推广到分段仿射(Piece-wise affine)和具有未知非线性输入的非线性系统中.
此外,迭代学习预测控制算法也适用于带约束的系统.通过把系统输入输出上的约束表达成问题(16)中的约束条件,这种方法可保证各种物理约束均得到满足.然而,在存在稳定性约束条件时,如何保证稳定性约束与系统物理约束不冲突,也就是如何保证优化问题解集非空,是一个重要的问题.文献[76]提出了二维可解性(Two-dimensional feasibility)这一概念,并给出了解决这类问题的基本框架,即在二维系统模型的基础上,增加一个零状态终端约束(Zero-terminal state constraint).文献[77]在文献[76]的基础上,将零状态终端约束扩展为椭圆不变集终端约束(Ellipsoid invariant set terminal constraint)(如图4所示),并提出了新的稳定性条件,从而增大可行域的范围,减少算法的保守性.

图4 带终端约束的迭代学习预测控制算法示意图Fig.4 Iterative learning predictive control with terminal constraints
2.4 批次过程控制技术应用
目前批次过程广泛应用在半导体制造、制药、塑料加工等领域.知名的自动化公司如西门子、ABB等都开发了专门的批次过程控制方案.表1显示了几家知名企业在批次过程控制方面的专利申请和购买情况.从此,不难看出,批次过程控制技术不只停留在理论阶段,在应用方面也已经初具规模.

表1 批次过程控制技术应用Table 1 Application of process control
3 展望与前景
过去三十年中,学者们在批次过程控制算法的研究上取得了不少成果,这使得批次过程得到了更广泛的应用,但仍存在着一些问题需要进一步的研究,其中包括以下几个方面.
3.1 不确定时长的批次过程控制
上文回顾的方法都是基于一个假设:每个批次有固定的时长.当批次过程的时长是由过程本身的状态决定时,初始状态的不一致或不重复的外部干扰会使得这一假设不成立.当该假设不成立时,原有的控制算法不再适用.以最简单的P类迭代学习控制为例,如图5所示,假设k批次的时长为T1,k+1批次的总时长为T2,且T1<T2.如式(1)所示,在时刻t(T1<t<T2),u(t,k+1)的取值与u(t,k)有关,但由于t>T1,此时u(t,k)的信息不可用.这种情况使得原本的设计方法行不通.原有的算法需要进行修正.文献[89−91]假设引起批次长度变化的因素是随机的,进而用0补齐较短的批次中缺失的跟踪误差信息,并对输入信号在批次方向上取平均.这类方法解决了信息缺失给控制器设计和收敛性分析带来的困扰,但这些工作大多假设系统动态特性沿批次方向是不变的.在实际的工业过程中,批次时长不定时,这一假设较难成立.从本质上来说,不等长系统只是一个近似重复的系统.因而,不等长问题衍生出一个新的研究课题,即如何利用这种近似重复特性来设计控制算法.

图5 不等长现象示意图Fig.5 Illustration of uneven length phenomena
3.2 针对非线性批次过程的稳定性研究
多数批次过程是具有较明显的非线性的.为了降低在线计算的复杂度,基于迭代学习控制的批次过程算法大多用一个线性时变模型来近似非线性系统.如文献[74]在不同的操作点将非线性模型线性化,从而得到一组线性近似模型,并基于这组线性模型进行控制算法的设计和稳定性分析.从应用的角度来看,当线性模型可以很好地近似非线性模型时,这类算法可以得到不错的控制效果.但从理论角度来看,这样的分析不够严谨,而如何建立起更为严谨的分析方法值得大家的关注.
除了对控制算法本身的研究,对与控制密切相关的模型的建立和设定值的优化也将是对批次过程研究的重点.这里我们简要列举两个方面.
3.3 基于学习的模型辨识方法
对于基于模型的控制算法来说,一个好的模型对于控制效果有着很大的影响.迭代学习控制的引入降低了控制算法对模型的依赖性,但好的模型依然可以加速算法的收敛和提高跟踪性能.对批次过程而言,建模的难点在于系统的时变特性,而如何利用重复性操作下得到的数据对时变系统建模是一个值得关注的问题.文献[92]用一个时间参数化的线性模型来刻画批次过程的时变特性.文献[93]从不同的角度出发,在每个时刻利用批次方向的数据采用递归最小二乘法进行辨识,从而得到一个时变模型.文献[94−96]在文献[93]的基础上,进一步考虑了基于部分先验知识的辨识算法和在线闭环辨识算法.目前这些算法多是基于线性系统,而如何将这类方法推广到非线性较强的批次过程值得进一步研究.
3.4 批次过程优化
如前所述,批次过程中的设定值通常不是一个固定值,而是通过优化质量或能量指标得到的设定值曲线.由于产品质量同控制变量的设定值之间的关系十分复杂,通常很难用简单的数学模型描述,如何设计和求解该优化问题是一个重要问题[93].解决这个问题的思路大体可以归纳为两类:1)基于模型的优化[97];2)基于测量值的优化[98].在基于模型优化中,为了避免由于模型的不准确而违反约束条件,研究者们通常采用鲁棒优化算法,但这会使得算法太过保守[99].因而,研究者们提出应用实时得到的测量数据做优化.其中一类比较重要的方法是无模型优化算法[100−101].这类算法利用测量数据来估计目标函数的一阶导数,进而利用梯度法求解优化问题.这类方法通常需要大量实验数据.文献[102]提出将迭代学习控制和极值搜索(Extremum seeking)[103]相结合来在线求解设定值曲线.如何将两种方法有机结合起来从而扬长避短值得大家关注.
此外,当产品配方改变时,控制器的设定值也需要相应地变化以保证稳定的产品品质.例如在注塑过程中,当模具形状或填充材料变化时,为了使产品质量达到一定标准,注射速度、保压压力、料筒温度的设定值也需要得到相应地调整.但这两组参数之间的关系十分复杂,通常需要大量实验数据来对这两组参数进行建模.考虑到某些批次过程在产品变化时,尽管过程特性有所变化,但依然存在一定程度的相似性,文献[104]提出基于过程相似特性的模型移植策略.这种策略的基本思想是在产品A和B具有相似性的前提下,利用产品A的实验数据对产品B进行建模,以减少对产品B建模所需的实验次数.文献[105−107]进一步提出了一系列方法来减少实验次数.目前,这一方向的理论研究和应用工作都还不够成熟,仍需要很多进一步的研究工作,例如如何界定产品的相似性,以及如何甄别出适合移植的数据.
4 结论
本文针对批次过程“多重时变”的特性,总结了近三十年来批次过程控制算法的发展.从直接应用连续过程的控制算法,到引入迭代学习控制,再到利用二维系统控制理论进行设计和分析,批次过程控制在理论和应用方面都获得了丰硕的成果.此外,本文还提出了批次过程在建模、优化及控制方面存在的几个问题和未来可能的发展方向,供大家参考和进一步讨论.
1 Stephanopoulos G.Chemical Process Control:An Introduction to Theory and Practice.Englewood Cliffs,N.J.:PTR Prentice Hall,1984.
2 Liu T,Gao F R.Industrial Process Identi fication and Control Design.Berlin:Springer-Verlag,2012.
3 Bonvin D.Control and optimization of batch processes.IEEE Control Systems,2006,26(6):34−45
4 Yang Y.Injection Molding Control:from Process to Quality[Ph.D.dissertation],Hong Kong University of Science and Technology,China,2004.
5 Camacho E F,Alba C B.Model Predictive Control.London:Springer Science&Business Media,2013.
6 Mayne D Q,Rawlings J B,Rao C V,Scokaert P.Constrained model predictive control:stability and optimality.Automatica,2000,36:789−814
7 Chen Hong,Liu Zhi-Yuan,Xie Xiao-Hua.Nonlinear model predictive control:the state and open problems.Control and Decision,2001,16(4):385−391(陈虹,刘志远,解小华.非线性模型预测控制的现状与问题.控制与决策,2001,16(4):385−391)
8 Qin S J,Badgwell T A.A survey of industrial model predictive control technology.Control Engineering Practice,2003,11(7):733−764
9 Xi Yu-Geng,Li De-Wei,Lin Shu.Model predictive control:status and challenges.Acta Automatica Sinica,2013,39(3):222−236(席裕庚,李德伟,林姝.模型预测控制–现状与挑战.自动化学报,2013,39(3):222−236)
10 Fan Jia-Lu,Zhang Ye-Wei,Chai Tian-You.Optimal operational feedback control for a class of industrial processes.Acta Automatica Sinica,2015,41(10):1754−1761(范家璐,张也维,柴天佑.一类工业过程运行反馈优化控制方法.自动化学报,2015,41(10):1754−1761)
11 He De-Feng.Stabilizing economic model predictive control of constrained nonlinear systems.Acta Automatica Sinica,2016,42(11):1680−1690(何德峰.约束非线性系统稳定经济模型预测控制.自动化学报,2016,42(11):1680−1690)
12 Morari M,Za firiou E.Robust Process Control.Englewood Cliffs,N.J.:Prentice hall,1989.
13 Zhou K M,Doyle J C.Essentials of Robust Control.Upper Saddle River,N.J.:Prentice Hall,1998.
14 Wang T,Gao H J,Qiu J B.A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control.IEEE Transactions on Neural Networks and Learning Systems,2016,27(2):416−425
15 Bellman R E.Adaptive Control Processes:A Guided Tour.Princeton:Princeton University Press,2015.
16 Kumar P R,Varaiya P.Stochastic Systems:Estimation,Identi fication,and Adaptive Control.Upper Saddle River,N.J.,USA:Prentice-Hall,Inc.,1986.
17 Yang Y,Gao F R.Injection velocity control using a selftuning adaptive controller.International Polymer Processing,1999,14(2):196−204
18 Yang Y,Gao F R.Adaptive control of the filling velocity of thermoplastics injection molding.Control Engineering Practice,2000,8(11):1285−1296
19 Nagy Z,Agachi S.Model predictive control of a PVC batch reactor.Computer&Chemical Engineering,1997,21(6):571−591
20 Nagy Z K,Braatz R D.Robust nonlinear model predictive control of batch processes.AIChE Journal,2003,49(7):1776−1786
21 Tian Y,Zhang J,Morris J.Modeling and optimal control of a batch polymerization reactor using a hybrid stacked recurrent neural network model.Industrial&Engineering Chemistry Research,2001,40(21):4525−4535
22 Mujtaba I M,Aziz N,Hussain M.Neural network based modelling and control in batch reactor.Chemical Engineering Research and Design,2006,84(8):635−644
23 Lee J H,Lee K S.Iterative learning control applied to batch processes:an overview.Control Engineering Practice,2007,15(10):1306−1318
24 Zhu Q,Xu J X,Huang D Q,Hu G D.Iterative learning control design for linear discrete-time systems with multiple high-order internal models.Automatica,2015,62:65−76
25 Wang D W.On D-type and P-type ILC designs and anticipatory approach.International Journal of Control,2000,73(10):890−901
26 Chen Y Q,Moore K L.PI-type iterative learning control revisited.In:Proceedings of the 2002 American Control Conference.Anchorage,AK,USA:IEEE,2002,3:2138−2143
27 Park K H.A study on the robustness of a PID-type iterative learning controller against initial state error.International Journal of Systems Science,1999,30(1):49−59
28 Chen Y Q,Gong Z M,Wen C Y.Analysis of a high-order iterative learning control algorithm for uncertain nonlinear systems with state delays.Automatica,1998,34(3):345−353
29 Yin S,Li X W,Gao H J,Kaynak O.Data-based techniques focused on modern industry:an overview.IEEE Transactions on Industrial Electronics,2015,62(1):657−667
30 Tanaskovic M,Fagiano L,Novara C,Morari M.Data-driven control of nonlinear systems:an on-line direct approach.Automatica,2017,75:1−10
31 Owens D H,Feng K.Parameter optimization in iterative learning control.International Journal of Control,2003,76(11):1059−1069
32 Owens D H.Norm optimal iterative learning control.Iterative Learning Control,London:Springer,2016.233−276
33 Zhao Y M,Lin Y,Xi F F,Guo S.Calibration-based iterative learning control for path tracking of industrial robots.IEEE Transactions on Industrial Electronics,2015,62(5):2921−2929
34 Son T D,Pipeleers G,Swevers J.Robust monotonic convergent iterative learning control.IEEE Transactions on Automatic Control,2016,61(4):1063−1068
35 Ge X,Stein J L,ErsalT,Goele P,SweversJ.Frequency-domain analysis of robust monotonic convergence of norm-optimal iterative learning control.IEEE Transactions on Control Systems Technology,2017.DOI:10.1109/TCST.2017.2692729
36 Gao F R,Yang Y,Shao C.Robust iterative learning control with applications to injection molding process.Chemical Engineering Science,2001,56(24):7025−7034
37 Xu Z H,Zhao J,Yang Yi,Shao Z J.Robust iterative learning control with quadratic performance index.Industrial&Engineering Chemistry Research,2012,51(2):872−881
38 Chi R H,Wang D W,Hou Z S,Jin S T.Data-driven optimal terminal iterative learning control.Journal of Process Control,2012,22(10):2026−2037
39 Chi R H,Hou Z S,Huang B,Jin S T.A uni fied data-driven design framework of optimality-based generalized iterative learning control.Computers&Chemical Engineering,2015,77:10−23
40 Xiong Z H,Zhang J.A batch-to-batch iterative optimal control strategy based on recurrent neural network models.Journal of Process Control,2005,15(1):11−21
41 Zhang J.Batch-to-batch optimal control of a batch polymerisation process based on stacked neural network models.Chemical Engineering Science,2008,63(5):1273−1281
42 Jia L,Shi J P,Chiu M S.Integrated neuro-fuzzy model and dynamic R-parameter based quadratic criterion-iterative learning control for batch process.Neurocomputing,2012,98:24−33
43 Jang J S R,Sun C T.Neuro-fuzzy modeling and control.Proceedings of IEEE,1995,83(3):378−406
44 Lee K S,Chin I S,Lee H J,Lee J H.Model predictive control technique combined with iterative learning for batch processes.AIChE Journal,1999,45(10):2175−2187
45 Natarajan S,Lee J H.Repetitive model predictive control applied to a simulated moving bed chromatography system.Computers&Chemical Engineering,2000,24(2−7):1127−1133
46 Lee S K,Lee J H.Convergence of constrained model-based predictive control for batch processes.IEEE Transactions on Automatic Control,2000,45(10):1928−1932
47 Chin I,Qin S J,Lee K S,Cho M.A two-stage iterative learning control technique combined with real-time feedback for independent disturbance rejection.Automatica,2004,40(11):1913−1922
48 Liu T,Gao F R,Wang Y Q.IMC-based iterative learning control for batch processes with uncertain time delay.Journal of Process Control,2010,20(2):173−180
49 Wang Y Q,Doyle F J.Indirect iterative learning control:application on arti ficial pancreaticβ-cell.In:Proceedings of the 2009 Chinese Control and Decision Conference.Guilin,China:IEEE,2009.1728−1733
50 Wang Y Q,Doyle F J.Stability analysis for set-point-related indirect iterative learning control.In:Proceedings of the 48th IEEE Conference on Decision and Control,Jointly with the 28th Chinese Control Conference.Shanghai,China:IEEE,2009.5702−5707
51 Yang Yue-Nan,Wang You-Qing.Internal model controlenhanced learning-type model predictive control:application to arti ficial pancreas.Control Theory&Applications,2012,29(8):1057−1062(杨跃男,王友清.内模强化学习型模型预测控制及其在人工胰脏上的应用.控制理论与应用,2012,29(8):1057−1062)
52 Wang Y Q,Yang Y N,Zhao Z.Robust stability analysis for an enhanced ILC-based PI controller.Journal of Process Control,2013,23(2):201−214
53 Liu T,Wang X Z,Chen J.Robust PID based indirecttype iterative learning control for batch processes with timevarying uncertainties.Journal of Process Control,2014,24(12):95−106
54 Kaczorek T.Two-dimensional linear systems.Advances in Control.London:Springer,1999.283−284
55 Du C L,Xie L H.H∞Control and Filtering of Two-Dimensional Systems.Berlin Heidelberg:Springer,2002.
56 Kurek J E,Zaremba M B.Iterative learning control synthesis based on 2-D system theory.IEEE Transactions on Automatic Control,1993,38(1):121−125
57 Shi J,Gao F R,Wu T J.Robust design of integrated feedback and iterative learning control of a batch process based on a 2D Roesser system.Journal of Process Control,2005,15(8):907−924
58 Liu T,Gao F R.Robust two-dimensional iterative learning control for batch processes with state delay and time-varying uncertainties.Chemical Engineering Science,2010,65(23):6134−6144
59 Shi J,Gao F R,Wu T J.From two-dimensional linear quadratic optimal control to iterative learning control.Paper 1.Two-dimensional linear quadratic optimal controls and system analysis.Industrial&Engineering Chemistry Research,2006,45(13):4603−4616
60 Shi J,Gao F R,Wu T J.From two-dimensional linear quadratic optimal control to iterative learning control.Paper 2.Iterative learning controls for batch processes.Industrial&Engineering Chemistry Research,2006,45(13):4617−4628
61 Shi J,Gao F R,Wu T J.Robust iterative learning control design for batch processes with uncertain perturbations and initialization.AIChE Journal,2006,52(6):2171−2187
62 Wang Y Q,Shi J,Zhou D H,Gao F R.Iterative learning fault-tolerant control for batch processes.Industrial&Engineering Chemistry Research,2006,45(26):9050−9060
63 Wang Y Q,Zhou D H,Gao F R.Iterative learning reliable control of batch processes with sensor faults.Chemical Engineering Science,2008,63(4):1039−1051
64 Zhang R D,Gan L Z,Lu J Y,Gao F R.New design of state space linear quadratic fault-tolerant tracking control for batch processes with partial actuator failure.Industrial&Engineering Chemistry Research,2013,52(46):16294−16300
65 Zhang R D,Lu J Y,Qu H Y,Gao F R.State space model predictive fault-tolerant control for batch processes with partial actuator failure.Journal of Process Control,2014,24(5):613−620
66 Gao M,Sheng L,Zhou D H,Gao F R.Iterative learning fault-tolerant control for networked batch processes with multirate sampling and quantization effects.Industrial&Engineering Chemistry Research,2017,56(9):2515−2525
67 Wang L M,Mo S Y,Zhou D H,Gao F R,Chen X.Delayrange-dependent robust 2D iterative learning control for batch processes with state delay and uncertainties.Journal of Process Control,2013,23(5):715−730
68 Wang L M,Yu J X,Shi J,Gao F R.Delay-range dependentH∞control for uncertain 2D-delayed systems.Numerical Algebra,Control and Optimization,2015,5(1):11−23
69 Shi J,Gao F R,Wu T J.Single-cycle and multi-cycle generalized 2D model predictive iterative learning control(2DGPILC)schemes for batch processes.Journal of Process Control,2007,17(9):715−727
70 Mo S Y,Wang L M,Yao Y,Gao F R.Two-time dimensional dynamic matrix control for batch processes with convergence analysis against the 2D interval uncertainty.Journal of Process Control,2012,22(5):899−914
71 Cao Z X,Yang Y,Lu J Y,Gao F R.Two-time-dimensional model predictive control of weld line positioning in biinjection molding.Industrial&Engineering Chemistry Research,2015,54(17):4795−4804
72 Wang Y Q,Zhou D H,Gao F R.Iterative learning model predictive control for multi-phase batch processes.Journal of Process Control,2008,18(6):543−557
73 Lu J Y,Cao Z Z,Wang Z,Gao F R.A two-stage design of two-dimensional model predictive iterative learning control for nonrepetitive disturbance attenuation.Industrial&Engineering Chemistry Research,2015,54(21):5683−5689
74 Liu T,Wang Y Q.A synthetic approach for robust constrained iterative learning control of piecewise affine batch processes.Automatica,2012,48(11):2762−2775
75 Li D W,Xi Y G,Lu J Y,Gao F R.Synthesis of real-timefeedback-based 2D iterative learning control-model predictive control for constrained batch processes with unknown input nonlinearity.Industrial&Engineering Chemistry Research,2016,55(51):13074−13084
76 Lu J Y,Cao Z X,Gao F R.A stable two-time dimensional(2D)model predictive control with zero terminal state constraints for constrained batch processes.IFACPapersOnLine,2015,48(8):514−519
77 Lu J Y,Cao Z X,Gao F R.Ellipsoid invariant set-based robust model predictive control for repetitive processes with constraints.IET Control Theory&Applications,2016,10(9):1018−1026
78 Gorinevsky D M.Iterative Learning Update for Batch Mode Processing,U.S.Patent 6647354,November 2003.
79 Takagi K.Position Control Apparatus Including Iterative Learning Circuit,Exposure Apparatus,Method for Manufacturing Device,and Iterative Learning Method for Use in Position Control Apparatus Having Iterative Learning Circuit Including Learning Filter,U.S.Patent 8676355,March 2014.
80 Nie J B,Sheh E D,Weerasooriy S S.Disk Drive Adapting Feed-Forward Compensation Using Iterative Learning Control Over Segments of Seek Length,U.S.Patent 8902535,December 2014.
81 Havlena V,Horak J,Jelinek J.Polymerization Process Controller,U.S.Patent 6106785,August 2000.
82 Austin D P.Batch Process for Re fining Used Oil,U.S.Patent WO/2002/011850,February 2002.
83 Kanodia H,Davidsson M H,Nair R,Poorman A,Ruhe J,Martin P M.System for Analyzing Batch Processes,U.S.Patent 7894918,February 2011.
84 Predina J P,Broberg H L.Tuned Open-Loop Switched to Closed-Loop Method for Rapid Point-to-Point Movement of a Periodic Motion Control System,U.S.Patent 6686716,February 2004.
85 Stevenson J F,Marsh G,LaSalle J C,Behi M.Recycle Methods for Water Based Powder Injection Molding Compounds,U.S.Patent 6776954,August 2004.
86 Himberg J,Mannila H,Korpiaho K,Toivonen H T T,Tikanmaki J.Method for Controlling Operation of a Mobile Device by Detecting Usage Situations,U.S.Patent 6912386,June 2005.
87 Finan D,McCann T.Method and System for a Hybrid Control-to-Target and Control-to-Range Model Predictive Control of an Arti ficial Pancreas,U.S.Patent WO/2014/099882,June 2014.
88 Dobbles J M,Kamath A U,Mahalingam A,Brauker J H.Integrated Insulin Delivery System with Continuous Glucose Sensor,U.S.Patent 9572935,February 2017.
89 Li X,Xu J,Huang D.An iterative learning control approach for linear systems with randomly varying trial lengths.IEEE Transactions on Automatic Control,2014,7:1954−1960
90 Li X F,Xu J Z,Huang D Q.Iterative learning control for nonlinear dynamic systems with randomly varying trial lengths.International Journal of Adaptive Control and Signal Processing,2015,29(11):1341−1353
91 Shen D,Zhang W,Wang Y Q,Chien C J.On almost sure and mean square convergence of P-type ILC under randomly varying iteration lengths.Automatica,2016,63:359−365
92 Xu Z H,Zhao J,Yang Y,Shao Z J,Gao F R.Optimal iterative learning control based on a time-parametrized linear time-varying model for batch processes.Industrial&Engineering Chemistry Research,2013,52(18):6182−6192
93 Cao Z X,Yang Y,Lu J Y,Gao F R.Constrained two dimensional recursive least squares model identi fication for batch processes.Journal of Process Control,2014,24(6):871−879 94 Cao Z X,Zhang R D,Lu J Y,Gao F R.Online identi fication for batch processes in closed loop incorporating priori controller knowledge.Computers&Chemical Engineering,2016,90:222−233
95 Cao Z X,Zhang R D,Lu J Y,Gao F R.Two-time dimensional recursive system identi fication incorporating priori pole and zero knowledge.Journal of Process Control,2016,39:100−110
96 Cao Z X,Yang Y,Yi H,Gao F R.Priori knowledge-based online batch-to-batch identi fication in a closed loop and an application to injection molding.Industrial&Engineering Chemistry Research,2016,55(32):8818−8829
97 Srinivasan B,Palanki S,Bonvin D.Dynamic optimization of batch processes:I.Characterization of the nominal solution.Computers&Chemical Engineering,2003,27(1):1−26
98 Srinivasan B,Palanki S,Bonvin D.Dynamic optimization of batch processes:II.Role of measurements in handling uncertainty.Computers&Chemical Engineering,2003,27(1):27−44
99 RuppenD,BenthackC,BonvinD.Optimizationof batch reactor operation under parametricuncertaintycomputational aspects.Journal of Process Control,1995,5(4):235−240
100 Kong X S,Yang Y,Chen X,Shao Z J,Gao F R.Quality control via model-free optimization for a type of batch process with a short cycle time and low operational cost.Industrial&Engineering Chemistry Research,2011,50(5):2994−3003
101 Yang Y,Yang B,Zhu S Q,Chen X.Online quality optimization of the injection molding process via digital image processing and model-free optimization.Journal of Materials Processing Technology,2015,226:85−98
102 Cao Z X,Durr H B,Ebenbauer C,Allgower F,Gao F R.Iterative learning and extremum seeking for repetitive timevarying mappings.IEEE Transactions on Automatic Control,2016,DOI:10.1109/TAC.2016.2633724
103 AriyurK B,KrsticM.Real-TimeOptimizationby Extremum-Seeking Control.Hoboken,N.J.:John Wiley&Sons,2003.
104 Lu J D,Yao K,Gao F R.Process similarity and developing new process models through migration.AIChE Journal,2009,55(9):2318−2328
105 Luo L K,Yao Y,Gao F R.Iterative improvement of parameter estimation for model migration by means of sequential experiments.Computers&Chemical Engineering,2015,73:128−140
106 Luo L K,Yao Y,Gao F R.Bayesian improved model migration methodology for fast process modeling by incorporating prior information.Chemical Engineering Science,2015,134:23−35
107 Luo L K,Yao Y,Gao F R.Cost-effective process modeling and optimization methodology assisted by robust migration techniques.Industrial&Engineering Chemistry Research,2015,54(21):5736−5748
