基于化学物质释放的五点傅里叶变换求解泊松方程的方法

徐朝辉 赵海生 许正文 吴健 冯杰 徐彬 马征征 黄文龙

(中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107)

引 言

在电离层化学物质释放引起的等离子体小尺度不均匀体数值模拟中,电势求解是非常重要的一环．在静电粒子模型中,静电力起着决定作用,已知电荷密度分布的情况下,不必求解复杂的麦克斯韦方程组,通过求解泊松方程,就能够获得空间电势分布,进而得到空间电场分布,可用于描述化学物质释放产生等离子体不均匀结构的动力学过程．通常求解泊松方程的方法有矩阵法、迭代法和谱方法[1-2]．

等离子体主要表现为集体运动特性,在等离子体粒子模拟中使用有限大小粒子可以使近距离碰撞作用极大降低,而不改变远程相互作用,从而使集体运动特性保留下来．粒子模拟中有限大小粒子的电荷不再是集中一点,而是按照一定的形状连续地分布在它的有限空间里,因而力的计算方法有很大的不同．因为力的计算采用卷积的形式,显然没有必要再像点粒子那样用两粒子作用力叠加的办法来计算,而用傅里叶变换的方法计算要简单很多,也就是说,求解泊松方程,不必再去使用精确的电荷密度,而只要将电荷密度在空间网格点上作近似的展开即可[3]．这样的展开一方面收敛快,另一方面不必使用偶极展开项,并且傅里叶变换方法编程程序简单,占用计算机处理器内存少,节约了粒子模拟的运算时间[4]．

快速傅里叶变换(Fast Fourier Transform,FFT)在空间网格点上求解泊松方程最早由Cooley、Tukey提出[5],后来Weaver在Cooley的基础上做了详细的离散傅里叶分析[6]．Birdsall 和 Langdon提出了经典的FFT解泊松方程的方法[7],这个方法推导方便,计算效率高,程序实现简单,成为国内外沿用至今的方法．近年来,随着离子模拟应用场景的推广,根据各种应用条件的不同也发展了几种其他的FFT求解泊松方程的方法[2]．

在将离子模拟方法引入电离层化学物质释放的数值模拟过程中,我们发现Birdsall方法在计算精度上有待提高,参考国内外相关文献[1,5-6],在经典谱方法的基础上[8],提出了一种新的FFT求解泊松方程的方法．结果表明,改进的方法精度更高,电势分布更符合解析值,为等离子体粒子模拟过程中静电模型的泊松方程求解提供了一种新的方法．

1 求解原理

首先给出电离层化学物质释放后系统中静电场电势的泊松方程:

(1)

ρ=ρe+ρx+ρO.

(2)

式中:ρ是电子和离子总的电荷密度;下标e、x、O分别代表电子、负离子和氧离子;ε0是真空介电常数．为了便于计算,这里模拟的系统是释放早期,约等于或少于负离子回旋周期的时间内电子和离子行为,但是忽略了扩散效应和电子吸附过程等其他因素的影响,并非是在整个释放稳定后的状态．

1.1 级数求导方法

级数求导法是一种常用的泊松方程求解方法[9],该方法的基本思路是通过FFT求得电荷密度和电势傅里叶级数的系数,得到电荷密度和电势的傅里叶级数;将得到的傅里叶级数代入泊松方程,可得到电势的傅里叶象函数对应关系;对电势的象函数做逆傅里叶变换,即可求得电势．以二维形式为例,对于周期系统,在满足Dirichlet条件下得到电势的傅里叶象函数:

(3)

式中:Pkx,ky为电荷密度的象函数;Nx和Ny为网格大小．可以看到,电势象函数在频域下为显式格式,求解十分方便．不过还需要注意到该方法可能引起吉布斯现象[10],所以需要一个额外的滤波器通过减小高阶傅里叶系数的方法来平滑边界,同时还要注意到对模型化简时,用到了近似替代的简化手段,这些操作使计算精度有所下降．

1.2 Birdsall 和 Langdon经典解法

Birdsall和Langdon给出了一种经典FFT求解泊松方程的方法[5],以二维形式为例,对于周期系统,求解泊松方程的基本流程[3]如图1所示．

图1 FFT方法求解电势的流程图

根据文献[5]可以得到,电势象函数的表达式为

(4)

可以看到,Birdsall方法中,电势象函数的计算过程有了很大简化,但同时要考虑网格大小Δx和Δy对近似替代精度的影响．

1.3 五点傅里叶变换方法

传统等离子体粒子模拟中FFT求解泊松方程的方法已经十分成熟[11],计算精确度在大多数情况下能够满足粒子模拟的需要．然而在开展电离层化学物质释放产生的电子密度空洞和等离子体云的小尺度扰动数值模拟仿真过程中,为了进一步精确模拟电子密度空洞边界不规则体的演化,得到不稳定性相干结构,本文提出一种改进的FFT求解泊松方程的方法,满足了化学物质释放早期演化过程模拟精度的需要．

对于周期边界条件下的二维系统,将式(1)差分得到

(5)

将式(5)用中心差分法继续分解,有

(6)

整理得到

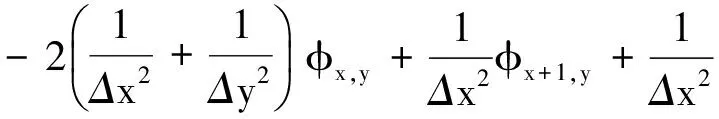
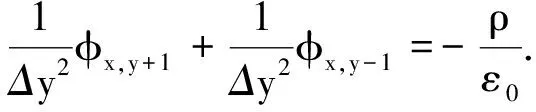
(7)

(8)

对式(8)化简,合并为三角函数形式有

(9)

在粒子模拟网格划分时,网格长度设为Δx=Δy,式(9)进一步化简为

(10)

此时,考虑到对二阶偏导做中心差分存在较大误差,为了弥补二阶差分对差分精度的影响我们引入差分误差修正项Rn(Rn≤ε),

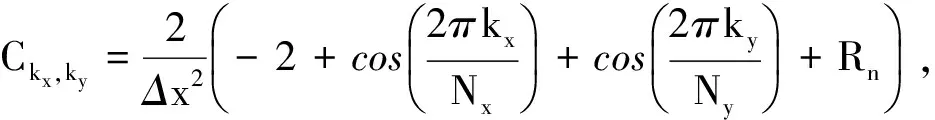
(11)

ε取值根据网格长度的不同而变化[4, 12]．则电势的傅里叶象函数可表示为

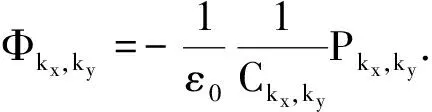
(12)

最后,对电势的傅里叶象函数求傅里叶逆变换得到电势φx,y的值．

改进的五点傅里叶变换方法,计算效率方面,只需一次插值、一次FFT和IFFT计算,仅比Birdsall方法和级数求导法多了一次插值运算．但是在傅里叶空间的系数运算中并未使用近似替代等处理方法,减小了非线性误差,同时对二阶差分误差采取了误差弥补措施,进一步提高了差分精度,同时保证了算法的稳定性．这种算法精度高、稳定性好,而且计算效率尚可,具有重要的理论意义和实际应用价值．

2 求解对比分析

2.1 单点电荷电势分布举例

下面使用三种方法求解一个简单例子,对比分析五点傅里叶改进方法和另外两种方法的优缺点．首先,建立一个64×64二维网格,在化学物质释放数值模拟领域,网格边界取为电子德拜长度,边界条件采用周期边界．电子和离子的总电荷密度分布已知,为了便于观察对比求解结果,这里用一个网格点(33,33)上20个单位正电荷的数密度给出,密度值为6.6942×10-13C/m2,如图2所示．

图2 点电荷密度二维分布

根据解析公式,可得到点电荷的电势

(13)

式中:q为点电荷的带电量,取值为20个单位正电荷;r为二维空间任一点距点电荷的距离．q>0时,电场中各点的电势都是正值,且随r的增加而减小．由式(13)可以得到在网格大小为64×64的系统中电势的解析分布,如图3所示,电势的最大量级在10-5．

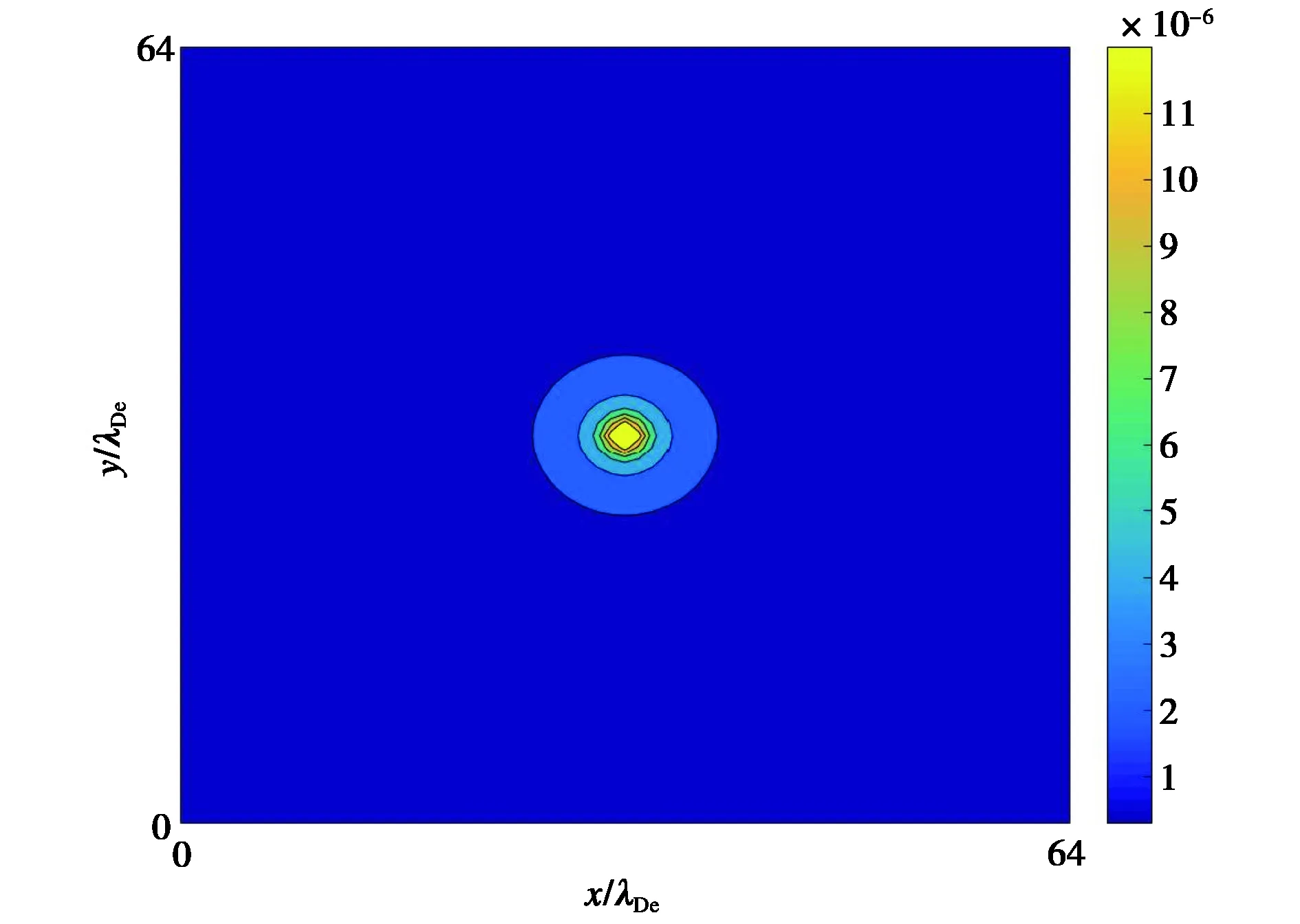
图3 解析方法得到的点电荷电势二维分布

根据点电荷密度分布,分别使用三种方法求解泊松方程,得到三种方法下电势的分布,如图4、5、6所示．五点傅里叶方法求得的电势最大值在10-7量级,Birds all方法和级数求导法求得的电势最大值在10-2量级,单纯从最大值误差精度看,五点傅里叶方法相比其他两种方法误差更小,更加趋近真实值．由图4可见,点电荷的电势梯度分布均匀,电势等值线轮廓近似圆形,电势关于点电荷对称分布,近似符合数值解析结果．与图3结果相比较,二者的电势空间分布结构基本一致,电势值与解析值之间的均方误差(Mean Square Error, MSE)为1.0539×10-12,电势的空间分布符合实际,其优势足以弥补小量级精度误差的缺陷．

图4 五点傅里叶方法得到的点电荷二维电势分布

图5为Birdsall经典方法得到的近似电势分布．电势分布近似为y=x对称分布,电势最大值约为10-2量级,与理论解析分布存在较大误差,电势值与解析值之间的MSE达到 1.2378×10-6,同时由于折叠计算导致电势空间分布失真,与解析电势分布差异较大．

图5 Birdsall经典解法得到的点电荷电势分布

由图6可以看到,级数求导方法得到的电势分布存在明显数值误差,电势最大值趋近10-2量级,而MSE达到8.4134×10-6,电势空间分布出现负值,与理论解析分布亦存在较大差异．

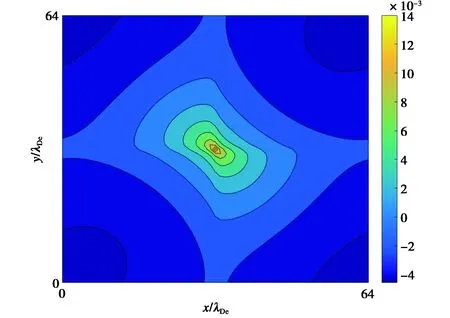
图6 级数求导方法得到的点电荷电势分布

为了研究三种方法数值解的精度,我们做了三种方法的误差对数(lg(e))曲线,如图7所示．从图7可以看到,五点傅里叶方法的误差对数远小于其他两种方法,且数值精度有了很大提高．

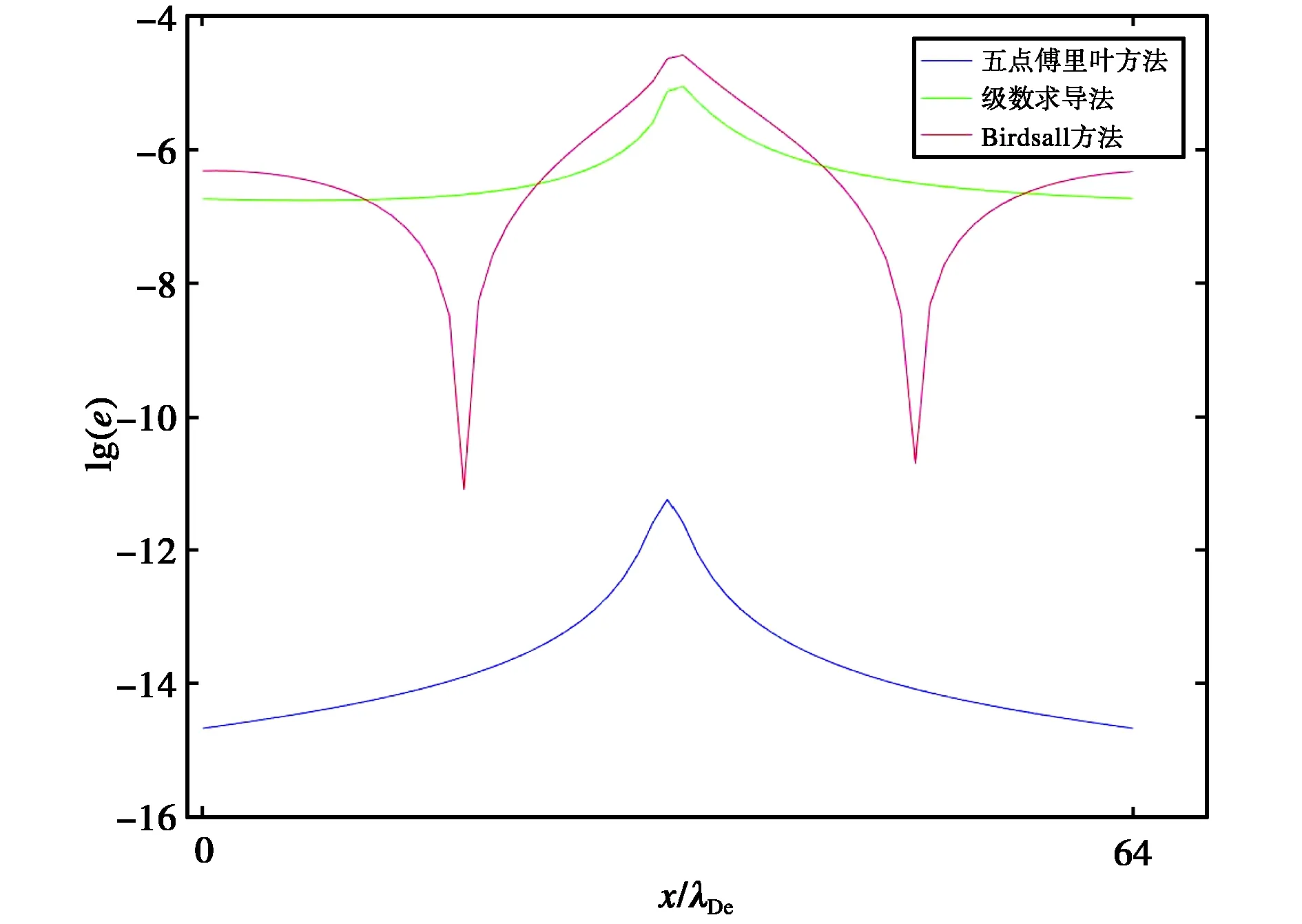
图7 三种方法的误差对数曲线

2.2 求解化学物质释放实际应用

将五点傅里叶变换方法代入中性气体化学物质释放产生密度空洞的静电全粒子模拟例子中,设网格为128×128,网格大小为电子德拜半径λDe,时间尺度为1/ωpe;周期边界条件下,电子、离子数密度分布已知,电子密度为中间区域为零,四周均匀分布,负离子密度为中间盘状区域均匀分布,正离子密度在全区域均匀分布[8]．在模拟系统启动时,系统呈整体电中性,电势能为零,如图8所示．

图9为利用五点傅里叶变换方法求得的化学物质释放后电势分布．在系统运行到ωpet=100时,空洞边界层开始出现明显的电势分界,此时负离子运动到边界层外,而电子由于磁场的束缚不能进入边界层,导致负电荷在边界层外积聚形成内外电势差,从而形成一个外向的电场．从图9可以看到,电势分布基本聚集在电子空洞的边界层,里面电势高外面电势低,电势分布细节清晰,符合理论推导．进而证明,我们采用五点傅里叶方法求解泊松方程满足系统的要求．

图8 初始时刻电子、负离子和氧离子密度分布(顺序从上到下)

图9 ωpet=100时系统电势分布

3 结 论

在化学物质释放粒子模拟中,针对粒子模拟仿真模型,本文研究了泊松方程的FFT方法求解问题,提出一种改进的FFT方法求解泊松方程,取消近似替代项,并引入误差修正项,消除非线性误差对计算结果的影响,在仿真案例中求得的点电荷泊松方程电势的MSE相对Birdsall方法和电势求导方法小6个量级,误差对数量级也远远小于这两种方法,同时电势空间分布更加符合实际．通过实际应用仿真模拟发现,仿真结果符合理论推导,结果证明五点FFT方法求得电势的精度符合化学物质释放早期小尺度不均匀体演化模拟的需要．

研究证明:改进的五点傅里叶变换方法在傅里叶空间的系数运算中并未使用近似替代等处理方法,减小了非线性误差,同时对二阶差分误差采取了误差弥补措施,进一步提高了差分精度,保证了算法的稳定性,这种算法精度高、稳定性好,而且计算效率尚可;采用改进的傅里叶变换方法求得电势的空间分布更接近解析法求解结果,精度更高,能够满足化学物质释放数值仿真的精度要求,具有重要的理论意义和实际应用价值．在未来的工作中该方法将应用于中性气体释放产生电子耗空的混合模型数值模拟,以及电子增强的化学物质释放数值仿真中．

[1] TREFETHEN L N. Spectral methods in Matlab[M]. Philadelphia:Society for Industrial &Applied, 2000.

[2] 马征征, 徐彬, 许正文, 等. 尘埃等离子体混合模型中电荷-电势问题的迭代法求解[J]. 电波科学学报, 2015, 30(3): 549-553.

MA Z Z, XU B, XU Z W, et al. Solving charge-potential issue in dusty plasma hybrid model by iteration method[J]. Chinese journal of radio science, 2015, 30(3): 549-553. (in Chinese)

[3] KRUER W L, DAWSON J M, ROSEN B, et al. The dipole expansion method for plasma simulation[J]. Journal of computational physics, 1973, 13(1): 114-129.

[4] 邵福球. 等离子体粒子模拟[M]. 北京: 科学出版社, 2002.

[5] COOLEY J W, TUKEY J W. An algorithm for the machine calculation of complex Fourier series[J]. Math comput. 1965.

[6] WEAVER H J. Applications of discrete and continuous Fourier analysis [M]. New York: Wiley, 1983.

[7] BIRDSALL C K, LANGDON A B. Plasma physics via computer simulation[M]. New York: Mcgraw-Hill Book Company, 1985.

[8] SCALES W A, BERNHARDT P A, GANGULI G, et al. Early time evolution of negative ion clouds and electron density depletions produced during electron attachment chemical release experiments[J]. Journal of geophysical research, 1994, 99(A1): 373-381.

[9] CHAE G S, SCALES W A, CHAIR C, et al. Numerical simulation of ion waves in dusty plasmas[D]. Virginia: Virginia Polytechnic Institute and State University, 2000.

[10] 卢文祥.信号分析[M].武汉: 华中科技大学出版社.2002.

[11] 蒋伯诚.计算物理中的谱方法[M]. 湖南科学技术出版社, 1988.

[12] 冯象初, 任春丽,尚晓清等.数值分析[M]. 西安电子科技大学出版社.2012.