一种高选择性的宽带滤波功分器

吴绍炜 张宏映 李蓉 魏玉龙 李晋军 唐聪

(1. 电子科技大学,成都 611731;2. 北方自动控制技术研究所,太原 030006)

引 言

自从1960年Wilkinson[1]功分器被设计出来,由于其结构简单以及端口之间良好的隔离度的优点,一直广泛应用于无线通信系统中．在传统的无线通信系统中,滤波器和功分器通常是级联在一起来达到滤波和功分的目的．但是,这样的措施会导致整个电路系统尺寸比较臃肿,并且会增加插入损耗．另一方面,由于目前无线系统小型化发展的需要,也要求无线系统中的器件具有小型化和多功能的特点．基于此目的,很多学者对同时具有滤波和功分功能的器件展开了研究,并取得了很大的进展．在文献[2-3]中,设计人员提出了一种基于谐振器的滤波功分器,该功分器可以抑制某些谐波．在文献[4-7]所提出的电路结构中,传统Wilkinson功分器中的四分之一波长变换器被替换为滤波器,并且滤波器两个端口的阻抗被调整到70.7 Ω,而非50 Ω．然而,以上这些报道的滤波功分器件的工作带宽较窄,并且这些器件的带外抑制也不够高．近些年来,为了实现宽带的滤波功分器,有关人员尝试了各种方法,包括在输出端口加上额外的枝节[8-9],加载环形谐振器结构[10],或者利用多层宽带渐变结构[11]．然而,以上这些措施虽然能够在一定程度上扩展工作带宽,但是器件的带外抑制度还不够高．另外,这些报道的器件的矩形系数也不够高,也就意味着它们的频率选择性有待改善．

为了解决以上宽带和带外抑制度的问题,本文设计了一种宽带、高选择性、高带外抑制度的滤波功分器．并利用奇偶模的方法,推导了设计公式．实测结果与软件仿真结果吻合,验证了该设计的有效性．

1 理论分析

传统的Wilkinson功分器及本文所提出的滤波型功分器的原理框图如图1所示．比较两个电路的原理图可以发现,将图1(a)中的四分之一波长传输线替换为中心枝节加载的带通滤波器,同时合理安排起着阻抗匹配与隔离作用的隔离电阻R的位置,即可得到图1(b)中的电路．图1(b)中的耦合线的特征阻抗分别为Zoei,Zooi(i=1, 2),中心加载开路枝节的特征阻抗为Z1,θ代表在中心频率f0处的电长度为90°．

由于图1(b)中的电路结构对称,为了便于分析,本文采取奇偶模的方法来推导该滤波功分器的设计公式．

(a) 传统Wilkinson功分器

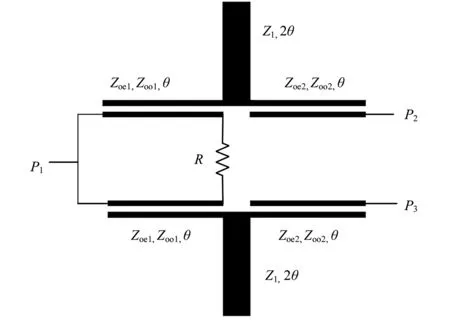
(b) 本文所提出的滤波型功分器图1 功分器的原理框图

1.1 奇次模等效电路

当在图1(b)中电路的P2端口与P3端口之间加奇次模激励(等幅反相)时,由于电路结构对称,在整个对称面上的电压为零．因此,在奇次模激励下的等效电路可以表示为图2(a)．根据电压与电流关系,Zin1的表达式可表示为

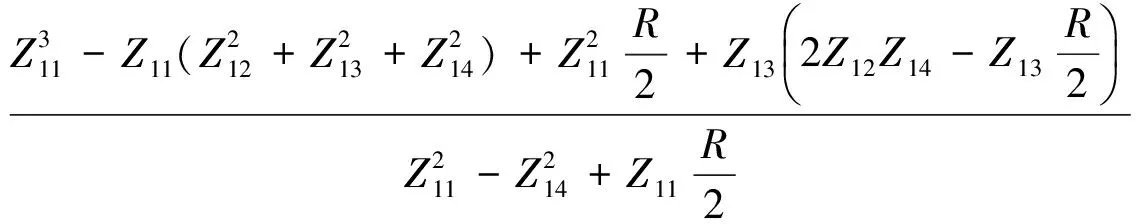
(1)

式中:

从中心点处向枝节加载看进去的阻抗为

Zin2=-jZ1cot(2θ)．

(2)

假设在端口2能够达到良好的阻抗匹配,则应该满足以下关系式:

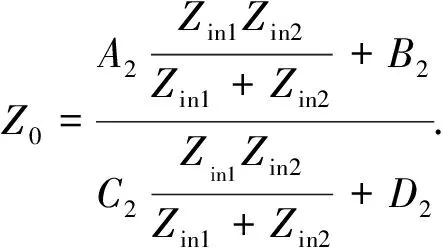
(3)

式中:

将式(3)中的实部与虚部分离,可以得到以下两个方程:

(4)

(5)

式中:

(Zoe2+Zoo2)2cos(2θ)+

j2Z0(Zoe2+Zoo2)sin(2θ);

N= j2(Zoe2+Zoo2)sinθ[2Zoe2Zoo2cosθ-

jZ0(Zoe2+Zoo2)sinθ]．

1.2 偶次模激励

当在图1(b)中电路的P2端口与P3端口之间加偶次模激励(等幅同相)时,由于流过电阻的电流为零,因此电阻可以去掉;另外,由于整个电路结构对称,可以沿着整个对称面切割．此时,端口P1处的负载为2Z0．故,在偶次模激励下的等效电路可以用图2(b)表示．

(a) 奇次模激励

(b) 偶次模激励图2 滤波型功分器在两种激励下的等效电路图

假设在端口P1处的阻抗完美匹配,则可以得到

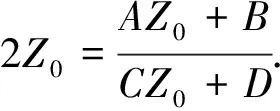
(6)

式中,ABCD为图2(b)虚线框图中电路的传输矩阵,且有

A1B1C1D1和A2B2C2D2分别表示平行耦合线1和平行耦合线2的传输矩阵．

对式(6)进行整理,并分离它的实部与虚部,可以得到以下方程:

(7)

1.3 传输零点

在上节对电路进行偶次模分析时,已经得到了端口P1和端口P2之间的ABCD传输矩阵．进一步地,端口P1与端口P2之间的传输系数可以由以上得到的参数推导出来,并表示如下:

(8)

故当式(8)等于零时,可以得出该电路的传输零点:

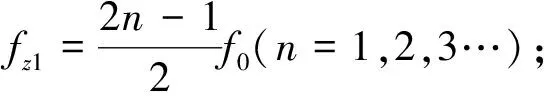
(9)

fz2=2nf0(n=1,2,3…)．

(10)

观察式(9)和(10)两式不难发现,该电路的传输零点与电路中的特征阻抗无关．传输零点的位置是固定的,它只与电路的中心工作频率f0有关．也就是说,一旦该电路的中心频率给定了,则电路的传输零点位置也就相应地固定了．

1.4 讨论

经过以上的理论分析,式(4),(5),(7)即是本文滤波功分电路的设计公式．观察以上三式可以发现,Z1并未出现在这三个表达式中．这表明Z1的值并不影响端口的阻抗匹配．为了进一步研究Z1的值对电路性能的影响,图3列出了在Zoe1,Zoo1,Zoe2和Zoo2的值分别固定在 200 Ω, 60 Ω, 180 Ω和80 Ω情况下,电路的频率响应随着Z1值变化时的理论曲线．

图3 所设计的滤波功分电路在Zoei和Zooi (i=1, 2)固定时随Z1值变化的理论响应曲线

由图3可以看出:随着Z1的增大,该电路的带宽变宽;在通带的上下边带均有传输零点,这非常有利于该电路的频率选择特性．另外,不难发现,这些零点的位置是固定的,并不随Z1的变化而移动,进一步验证了上文中的理论分析．

为了进一步说明怎么设计该滤波功分器,将设计步骤总结如下:

1)根据指标要求,确定中心频率f0,电长度θ,带宽WB．调整Z1的值以满足带宽要求;

2)根据式(4)和(7)中的条件,调整耦合线的特征阻抗值,以满足带内回波损耗的要求;

3)根据式(5)计算出隔离电阻R的值;

4)整体仿真优化以达到最佳性能．

2 实验测试

为了验证上文设计思路的有效性,依据上文的理论分析,设计并加工了一个中心频率f0为2.97 GHz的滤波功分器．采用的基板是RF-35,介电常数是3.5,基板厚度为0.508 mm,介质损耗角正切为0.0018．根据上文推导的理论公式(4)、(5)和(7),并考虑到加工精度(最小加工缝隙和线宽均为0.1 mm),所选择的设计参数是Z1=30 Ω,Zoe1=193 Ω,Zoo1=63 Ω,Zoe2=179 Ω,Zoo2=80 Ω,R=338 Ω (在实际的电路中选择的阻值为330 Ω)．因为在实际的微带耦合线中奇次模与偶次模的相速并不相等,这会导致在2f0处出现寄生通带．为了抑制此现象,部分输入端的耦合线折叠起来补偿奇次模与偶次模之间的相速差．

图4是所加工电路的版图及实物照片．详细的尺寸信息列在表1中．该电路的有效电路面积为0.46λg×0.53λg,其中,λg为中心频率f0处的导波波长．

(a) 版图

(b) 实物照片图4 设计加工的滤波功分器的版图和实物照片

表1 所加工电路的具体尺寸参数 mm

该器件是由安捷伦N5244A网络分析仪测量的．测量与仿真结果均描绘在图5中．由测试结果可知:中心频率为2.97 GHz,1 dB通带为2.05 GHz到3.89 GHz,相对带宽为62%;S21和S31在中心频率处的插损分别为3.72 dB和3.9 dB;带内回波损耗优于13.5 dB;在低频带的带外抑制优于38.2 dB,上边带从4.34 GHz到7.92 GHz (2.67f0)带外抑制优于31.4 dB;两个端口之间的隔离度优于19.2 dB．另外,由图5还可知,在该功分器的工作频带内,测试结果的极点个数少于仿真结果的极点个数.这是由于加工或者装配误差引起的,但这不影响该功分器的整体性能．总之,整体上仿真结果与测试结果吻合良好,验证了本文设计思路的正确性．

为了描述器件的频率选择特性,定义矩形系数如下:

(11)

式中:Δf40dB表示比中心频率处的插损下降40 dB时通带的带宽;Δf3dB表示比中心频率处的插损下降3 dB时通带的带宽．式(11)表明,k的值是小于1的,k的值越接近于1代表该器件的选择性越好,k的值越接近于0代表该器件的选择性越差．

表2给出了本文设计加工的滤波功分器件与之前公开报道的同类器件之间的性能对比．由表2可知,该器件同时具有较宽的通带、良好的频率选择特性、很高的带外抑制、较宽且较深阻带的优良特性．

(b) S22,S33和S23图5 所加工的滤波功分器的仿真与测试结果对比

表2 所设计加工的电路器件与之前报道的器件的性能对比

3 结 论

针对无线通信系统小型化发展的趋势,本文设计了一种同时具有滤波和功分功能的器件,它可以大大减小电路的尺寸和插入损耗．利用奇偶模的方法,推导了设计公式．最后为验证本设计思路的有效性,设计并加工了一个工作在2.97 GHz的滤波功分器．实验测试结果与仿真结果吻合良好．与之前公开报道的同类器件相比,本文所设计的器件具有宽带、高频率选择性、高带外抑制度的优点,特别适用于小型化射频前端系统中．未来的研究将扩展阻带的带宽,以使得该器件能够应用于未来多频带通信系统中．

[1] WILKINSON E J. An N-way hybrid power divider [J]. IEEE transaction on microwave theory and techniques, 1960, 8(1): 116-118.

[2] ZHANG X Y, WANG K X, HU B J. Compact filtering power divider with enhanced second-harmonic suppression [J]. IEEE microwave wireless component letters, 2013, 23(9): 483-485.

[3] CHEN C F, HUANG Y, SHEN T M, et al. Design of miniaturized filtering power dividers for system-in-a-package [J]. IEEE transaction on microwave theory and techniques, 2013, 3(10): 1663-1672.

[4] SHAO J Y, HUANG S C, PANG Y H. Wilkinson power divider incorporating quasi-elliptic filters for improved out-of-band rejection[J]. Electronics letters, 2011, 47(23): 1288-1299.

[5] CHAO S F, LI Y R. Miniature filtering power divider with increased isolation bandwidth [J]. Electronics letters, 2014, 50(8): 608-610.

[6] LI Y C, XUE Q, ZHANG X Y. Single- and dual-band power dividers integrated with bandpass filters[J]. IEEE transaction on microwave theory and techniques, 2013, 61(1): 69-76.

[7] SONG K J. Compact filtering power divider with high frequency selectivity and wide stopband using embedded dual-mode resonator[J]. Electronics letters, 2015, 51(6): 495-497.

[8] ZHANG B, LIU Y N. Wideband filtering power divider with high selectivity[J]. Electronics letters, 2015, 51(23):1950-1952.

[9] CHAO S F, LI Y R. Filtering power divider with good isolation performance[J]. Electronics letters, 2014, 50(11): 815-817.

[10] GAO S S, SUN S, XIAO S Q. A novel wideband bandpass power divider with harmonic-suppressed ring resonator[J]. IEEE microwave wireless component letters, 2013, 23(3):119-121.

[11] SONG K J, XUE Q. Novel ultra-wideband (UWB) multilayer slot-line power divider with bandpass response[J]. IEEE microwave wireless component letters, 2010, 20(1):13-15.