基于解析积分的TDSBR算法及其在目标散射中的应用

申宁 魏兵

(1. 西安电子科技大学物理与光电工程学院,西安 710071; 2. 西安电子科技大学信息感知技术协同创新中心, 西安 710071; 3. 西安邮电大学电子工程学院,西安 710121)

引 言

随着短脉冲和超宽带雷达在工程中的广泛应用,目标时域电磁散射的计算分析越来越受到重视.常用的时域数值方法[1]有时域矩量法(Time Domain-Method of Moment,TD-MOM),时域有限元法(Time Domain-Finite Element Method,TD-FEM),时域有限差分(Finite Difference Time Domain,FDTD)方法等.数值方法计算精度高,但是要消耗较多的内存,适用于求解电尺寸相对较小目标的电磁问题.电大尺寸目标电磁特性的研究常常采用高频方法.常见的时域高频方法有时域物理光学(Time Domain Physical Optics,TDPO)法[2],时域等效边缘电流(Time Domain Equivalent Electric Current,TDEEC)方法,时域几何绕射(Time Domain Geometric Theory of Diffraction,TDGTD)方法,时域弹跳射线(Time Domain Shooting and Bouncing Rays,TDSBR)方法等等.与时域数值方法相比,时域高频近似方法具有计算内存需求小、计算速度快的优点.

TDSBR是弹跳射线(Shooting and Bouncing Rays,SBR)法和TDPO方法相结合的时域算法.SBR法将入射的平面波等效为大量离散的射线管来模拟入射电磁波在目标中传播的情况,并采用TDPO方法积分求解散射场,特别适合于计算目标几何结构之间的多次反射场,具有物理概念清晰、精度高、容易实现等优点.传统的SBR方法为满足准确度要求,射线管的尺寸至少为入射电磁波波长的十分之一.对于电大复杂目标,射线数量庞大,计算效率低.为提高SBR方法的计算效率,许多学者提出了改进方案.Suk[3]等于2001年提出了多分辨率网格法,多分辨率加速技术提高了计算效率.然而该算法中射线管太大可能导致SBR方法无法捕捉到目标的一些细小几何结构,有损计算精度.2013年殷宏成[4]等提出了一种自适应射线管分裂算法,将射线管依据其在实际追踪过程中的情况分裂成若干个子射线管,这种方式不仅能保证计算精度,还能显著降低待追踪射线管数量.另外为了加速射线和目标求交测试的效率,Gao等人利用KD-tree进行加速求交[5],Tao等人用GPU对射线跟踪进行了加速[6].

本文将基于解析积分的TDPO算法和SBR方法相结合,给出了一种基于解析积分的TDSBR算法.与传统的TDSBR算法相比,本文方法可以明显减少射线管数量,在保证计算精确度的前提下提高电大尺寸目标电磁特性的计算效率.

1 时域弹跳射线(TDSBR)法

TDSBR方法是一种求解复杂目标多次散射的经典时域高频方法.TDSBR方法基本原理是:首先是射线管的生成,在垂直于入射方向上定义虚拟孔径面(等相位面).考虑到计算的精确性,虚拟孔径面需以波长的十分之一来划分射线管,本文射线管形状取为三角形.其次,对每一射线管的角点射线进行追踪,直到射出目标为止,记录角点射线的最终出射位置.然后,追踪射线管中心点发出的射线,与目标相交时利用几何光学法计算反射场.同时考虑射线管发散、极化和介质反射系数等因素,并记录射线管中心点的出射场;最后,采用解析TDPO积分计算该射线管在接收方向上的散射场,将所有射线管的远区散射场叠加,即得到目标总的远区散射场.弹跳射线方法主要包括三个主要部分:射线管的生成、射线管的追踪、口径面相关的积分计算,如图1所示.

图1 时域弹跳射线方法

1.1 射线场强的追踪

在角点射线跟踪结束后,确定有效射线管,选取其中心射线的场强进行跟踪计算,直到中心射线不再与目标相交或达到终止条件才停止追踪.射线管在传播过程中,第i+1次的交点ri+1处的场值可以通过第i次的交点ri处的场值递推:

E(ri+1)=(DF)i(R)iE(ri)e-j,φ.

(1)

式中:(R)i为ri处的反射系数矩阵;由传播路径引起的相位变化

φ=kr·(ri+1-ri)+ki·ri;

(2)

(DF)i为ri处的散度因子,用于描述射线管束中场强的变化,由几何光学可得到.在射线管发出时,面元被赋予了一定的能量,传播过程中总能量不变,随着横截面积发生变化,随之改变的是单位面积的能量,散度因子(DF)i就是用来描述这种变化[7],

(3)

1.2 远场解析积分计算

在入射场已知的情况下,完成射线追踪后,可由TDPO积分求得每一个射线管在远区产生的散射场.

TDPO算法求解时,积分区域就是射线管最后一次投影在目标的面积.传统的TDPO算法为了计算精度,需要将射线管离散划分取入射电磁波波长的十分之一,射线管投影面元中每一点的入射场大小看作是一致的,或者采用高斯积分的办法,用三角形射线管面元上多个特征点的场来拟合整个射线管的远场散射.本文采用解析的TDPO算法[8]计算,可明显减少射线管数量,提高计算效率.

考虑多次反射时的情况,如图2所示,TDPO方法观察点的场是目标上射线管最后一次反射时照亮面积积分的累加结果,远区散射电场可以由式(4)计算

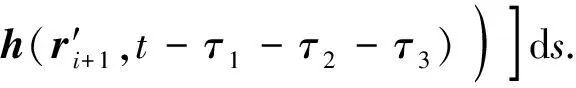
(4)

图2 TDPO算法各参量示意图

(5)

式中:ki为射线管初始入射方向;kri为射线管第i次反射时的方向,也是第i+1次反射时的入射方向;rre为源点所在的空间位置.

对于单个射线管,式(4)中的入射磁场方向、射线管面元法向以及散射方向都是已知的,即散射场公式可以改写成

(6)

式(6)中ds在积分计算时需向各个坐标面投影，如果投影到xoy平面，时间延迟用位置坐标表示，即

t-τ1-τ2-τ3=t+ax+by+c.

(7)

式中a、b、c为常数，可由式(5)计算得到.

入射波为微分高斯脉冲时,经过积分运算,最终得到散射场表达式如下[8]:

(8)

其中

(9)

式中:τ为入射波脉冲宽度;L1、L2和a1x+b1、a2x+b2分别为三角形射线管投影到xoy坐标面后沿着x轴的顶点坐标位置和对应的三角形边的直线方程．对单个射线管而言,在式(8)的求解过程中脉冲宽度、时间变量均由外界给定,与射线管本身尺寸大小无关.因此,在保证计算精度的情况下尽可能使射线管划分尺寸放大,从而减少对计算机内存的需求.

2 算例分析

图3 二面角的后向散射时域波形

在上述情形下,二面角的后向RCS的解析解为[9]

(10)

式中:L、M为矩形二面角反射器的长和宽;λ为入射波波长.图4为二面角的后向RCS随频率的变化情形.图中实线、三角形和圆点分别表示本文方法、传统方法和解析结果.可见,几种方法的计算结果吻合.

图4 二面角的后向RCS

算例2:金属角反射器的后向RCS.角反射器由三个5 m×5 m的平面组成.入射波为微分高斯脉冲,入射方向θ=45°,φ=45°(见图5),后向散射.传统TDSBR算法需要按照λ/10离散大约300 000个射线管,本文方法按照λ/6离散大约108 000个射线管.如图5所示为采用解析TDSBR计算θθ极化时三面角后向散射的时域波形.

图5 三面角的后向散射时域波形

图6为角反射器后向RCS随频率的变化曲线与商业软件FEKO计算结果的对比.由图可见,两种方法的计算结果吻合.此时本文方法射线管的数量仅为传统TDSBR射线管数量的1/3.

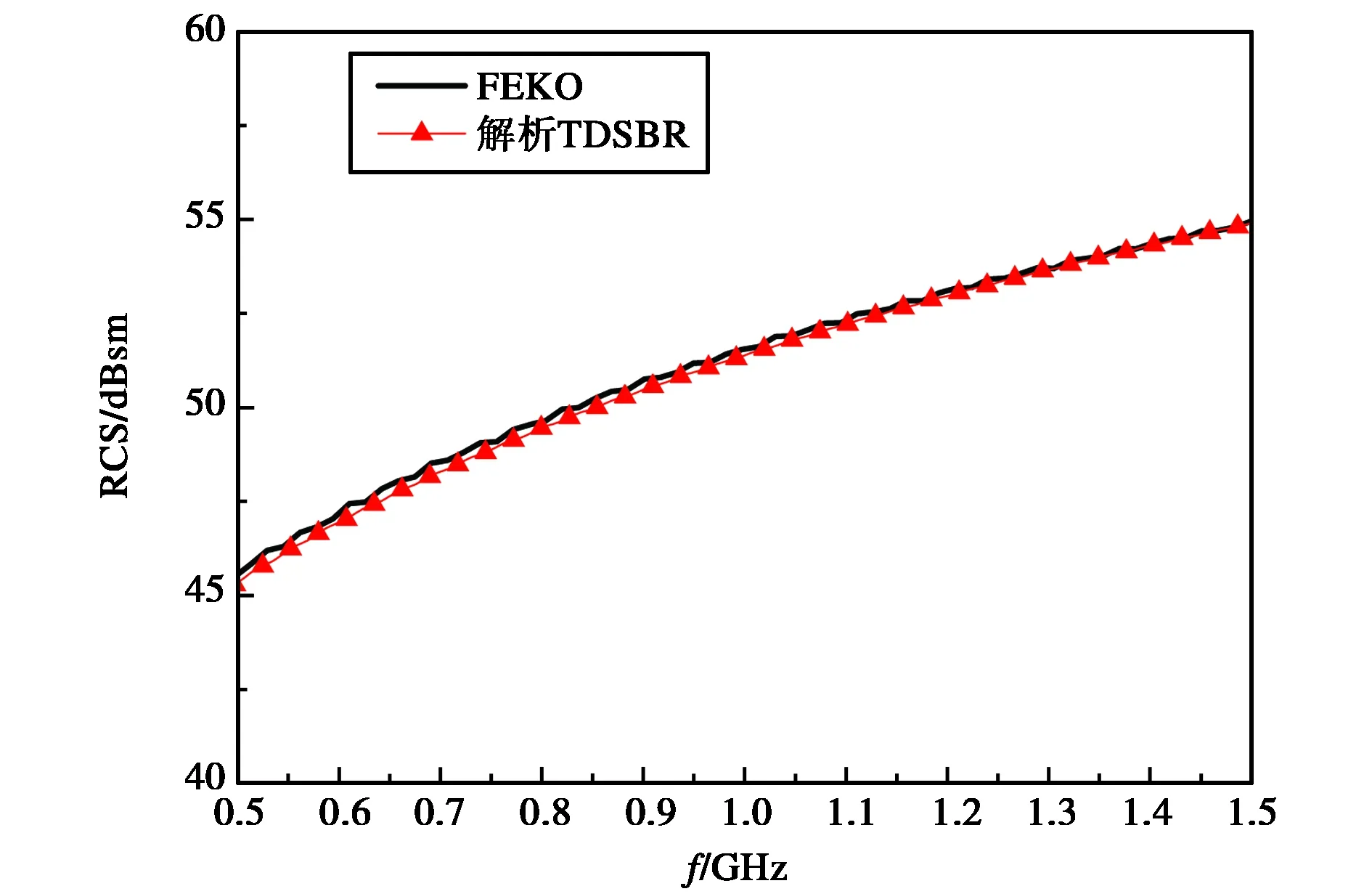
图6 三面角的后向RCS

算例3:双脊喇叭天线的后向散射.喇叭天线的口径面为12 cm×10 cm,长30 cm.模型离散为3 317个面元,如图7所示.入射波为微分高斯脉冲,沿着双脊喇叭天线口径垂直入射,后向散射.射线跟踪时反射次数上限取为3次.考虑到模型的复杂性,按照λ/10离散约6 000个射线管.图8为采用解析TDSBR计算θθ极化时后向散射的时域波形.图9为采用相同射线管划分时,解析TDSBR、传统TDSBR方法计算后向RCS随频率的变化曲线.从图中可以看出传统TDSBR与解析TDSBR计算结果在入射波频率为11 GHz以前基本吻合,之后传统TDSBR计算结果出现强烈的不稳定性.可见本文方法比传统方法更为稳定.

图7 双脊喇叭天线模型

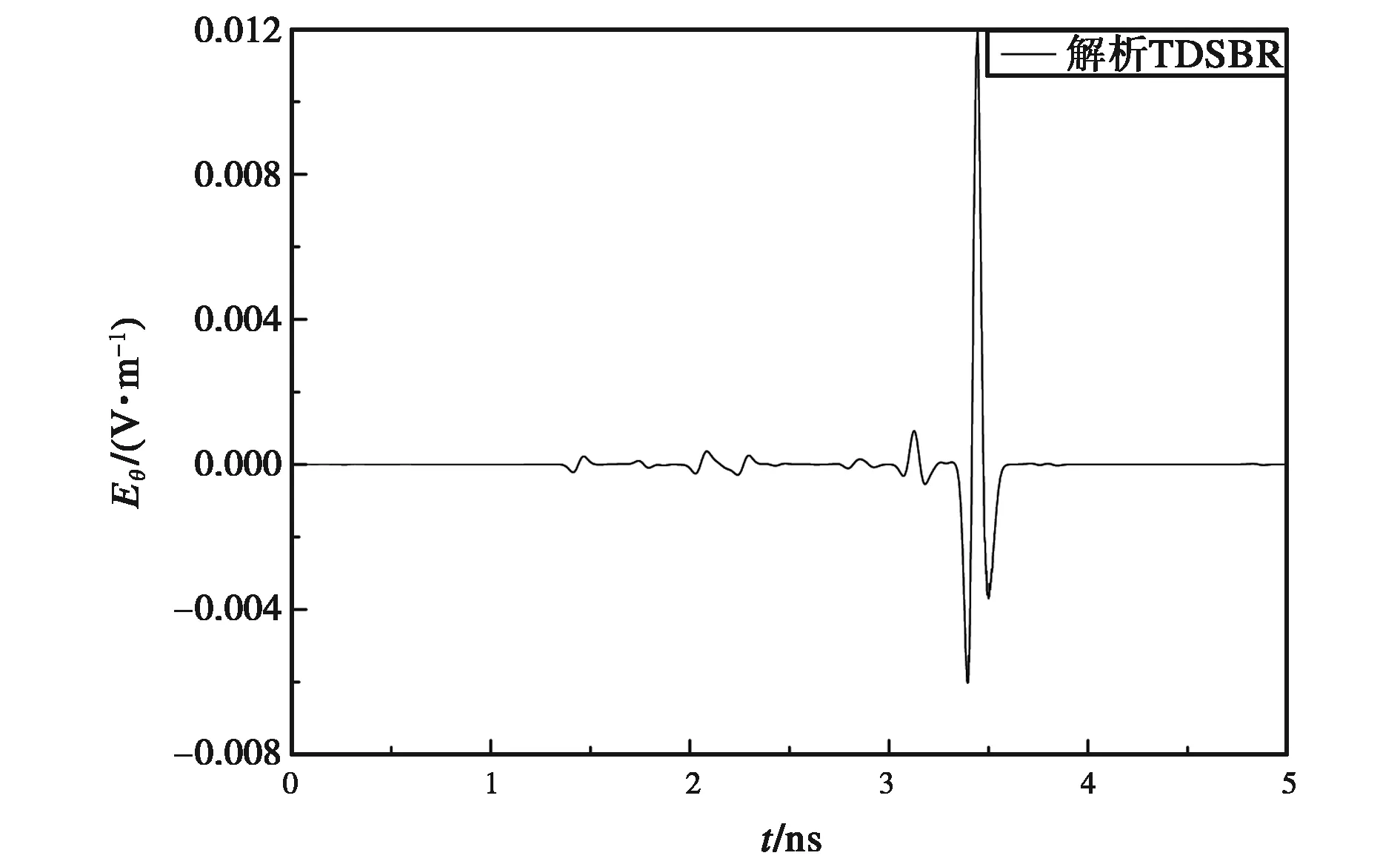
图8 双脊喇叭天线的后向时域散射波形

图9 双脊喇叭天线的后向RCS

图10为解析TDSBR计算按不同尺度划分射线管时RCS的对比,从图中可以看出按照λ/8划分射线管的计算结果与λ/10,λ/15划分是基本一致.图11 为传统TDSBR计算按不同尺度划分射线管时RCS的对比,从图中可以看出射线管λ/15划分时,高频区域的震荡才消失.由此可见,对复杂模型采用解析TDSBR计算结果比较稳定,与传统TDSBR比较,可用较少的射线管得到较精确的计算结果.

图10 解析TDSBR不同射线划分RCS的对比

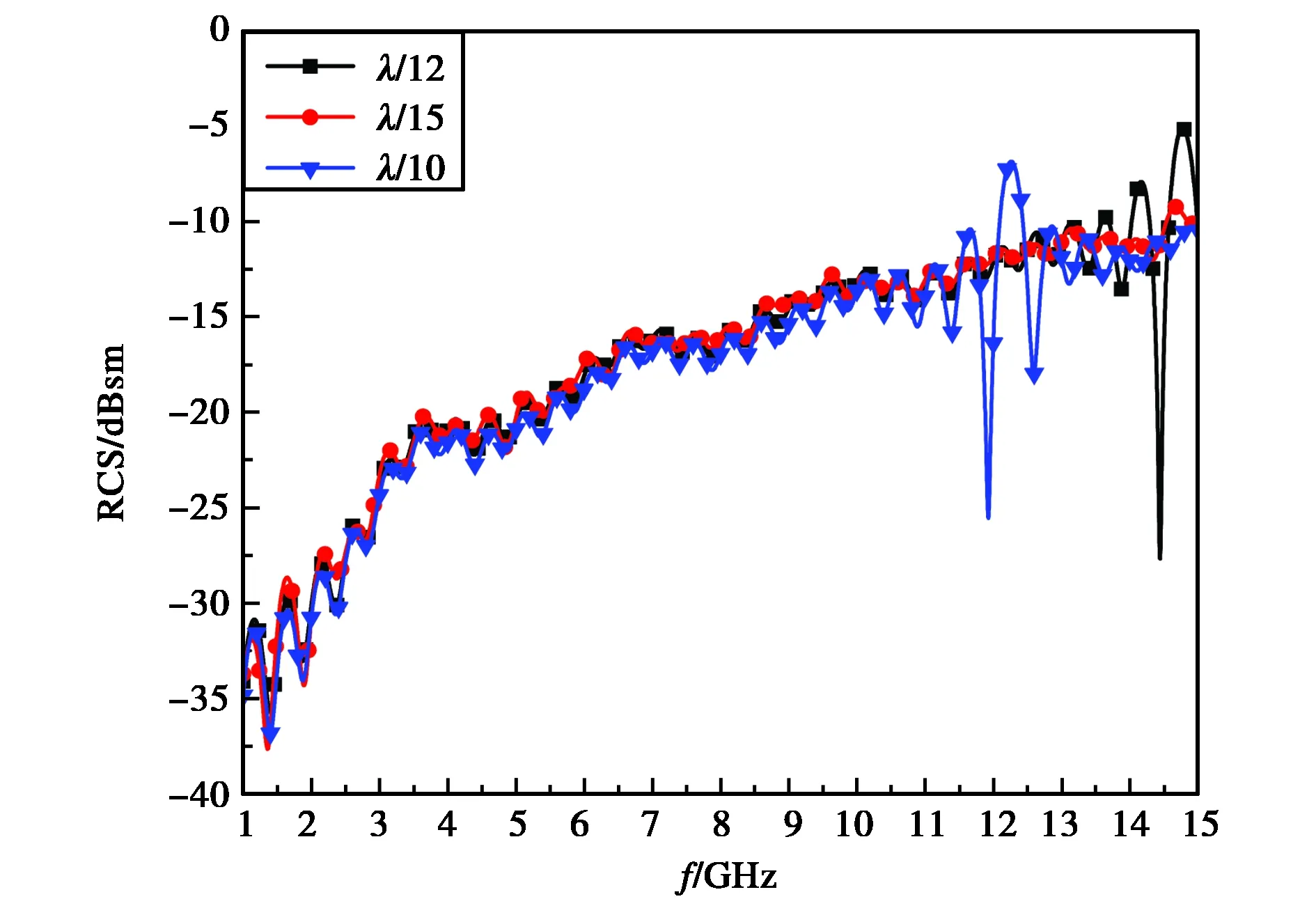
图11 传统TDSBR不同射线划分RCS的对比

3 结 论

时域弹跳射线法的优点是在处理电大尺寸目标时计算速度快、所需内存少、一次计算能得到宽频带RCS.但是庞大的射线管数目和耗时的射线与目标求交测试,使得计算效率低.文中的时域弹跳射线法采用解析TDPO积分计算目标的远区散射场,算例表明在保证计算精度的前提条件下,使得射线管的划分可不必取入射电磁波波长的十分之一,明显减少了射线管的数量,计算稳定性较好,提高了计算效率.

[1] 葛德彪, 魏兵. 电磁波时域计算方法[M]. 西安:西安电子科技大学出版社,2014.

[2] 杨凌霞, 葛德彪, 魏兵. 电大目标电磁散射的TDPO分析 [J]. 电波科学学报, 2007, 22(4): 552-556.

YANG L X, GE D B, WEI B. Analysis of large-scale EM scattering problems by using TD-PO method[J]. Chinese journal of radio science, 2007, 22(4): 552-556. (in Chinese)

[3] SUK S H, SEO T I, PARK H S, et al. Multi-resolution grid algorithm in the SBR and its application to the RCS calculation[J]. Microwave and optical technology letters, 2001, 29(6):394-397.

[4] 殷红成, 朱国庆, 董纯柱, 等. 基于自适应射线管分裂的多次反射计算方法[J]. 系统工程与电子技术, 2013,35(4):700-705.

YIN H C, ZHU G Q, DONG C Z, et al. Efficient multi-reflection computational method based on adaptive ray tube splitting[J]. Systems engineering and electronics, 2013, 35(4):700-705. (in Chinese)

[5] GAO P C, TAO Y B, LIN H. Fast RCS prediction using multiresolution shooting and bouncing ray method on the GPU[J]. Progress in electromagnetics research, 2010, 107(4): 187-202.

[6] TAO Y B, LIN H, BAO H J. GPU-based shooting and bouncing ray method for fast RCS prediction[J]. IEEE transactions on antennas and propagation, 2010, 58(2): 494-502.

[7] 张磊, 侯兆国, 董纯柱, 等.含曲面介质结构复杂目标电磁散射计算的射线追踪方法[J]. 电波科学学报, 2016,31(3): 546-552.

ZHANG L, YAO Z G, DONG C Z, et al. Ray tracing method for electromagnetic scattering computation from complex target with curved surface dielectric structure[J]. Chinese journal of radio science, 2016, 31(3):546-552. (in Chinese)

[8] 覃璐瑶, 魏兵, 边成, 等. 一种基于解析积分的TDPO算法及其在散射问题中的应用[J]. 电波科学学报, 2016,31(3): 508-511.

QIN L Y, WEI B, BIAN C, et al. A TDPO algorithm based on analytic integral and its application in scattering problems[J]. Chinese journal of radio science, 2016, 31(3): 508-511. (in Chinese)

[9] 阮颖铮. 雷达截面与隐身技术[M]. 北京: 国防工业出版社, 1998.

[10] 丁建军, 陈磊, 刘志伟, 等. 基于时域弹跳射线法分析电大尺寸目标的散射[J]. 系统工程与电子技术, 2010,32(9): 1846-1849.

DING J J, CHEN L, LIU Z W, et al. Analysis of electromagnetic scattering of electrically large objects with time domain shooting and bouncing rays method[J]. Systems engineering and electronics, 2010, 32(9): 1846-1849. (in Chinese)

[11] 丁建军, 刘志伟, 徐侃, 等. 基于高频方法分析电大尺寸目标的散射,系统工程与电子技术, 2010, 32(11): 2309-2312.

DING J J, LIU Z W, XU K, et al. Application of high frequency methods for scattering analysis of electrically large objects[J]. Systems engineering and electronics, 2010, 32(11): 2309-2312. (in Chinese)