有限域上一类1-生成元准扭转码的计数问题
2017-03-09吕京杰
吕京杰
( 山东理工大学 理学院,山东 淄博 255049)
有限域上一类1-生成元准扭转码的计数问题
吕京杰
( 山东理工大学 理学院,山东 淄博 255049)
在准扭转码的指标l与有限域Fq的扩张次数L互素的情况下,给出了有限域上任意长度的具有相同校验多项式的不同1-生成元准扭转码的计数公式.通过建立集合之间的双射,间接地解决了有限域上1-生成元扭转码的计数问题.
1-生成元准扭转码;任意长度;计数公式
近些年来,已有多篇文章探讨了扭转码(QT)的相关问题.研究QT码的原因主要有以下几个方面:首先QC码具有良好的代数结构、易于编码和译码工作的展开[1],其次QT码中含有大量性质优良的线性码[2],然后QT码和卷积码是密切相关的[3].在参考文献[4]中,高健等讨论了当QT码的分组码长和有限域特征互素时,关于有限域上1-生成元的QT码的计数问题.Jia[5]研究了任意长度QT码的结构特性,Jia首先运用中国剩余定理将QT码分解成扩域上一些线性码的直和,然后通过广义的离散傅里叶变换构造QT码.然而,Jia并没有讨论有限域上任意长度的1-生成元QT码的计数问题.本文将对这一问题进行深入探讨,我们给出了在特定情况下,任意长度的1-生成元QT码的计数公式,其可作为参考文献[4]和[5]的有效补充.
1 预备知识
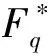
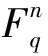

c=(c0,0,c0,1,…,c0,l-1,c1,0,c1,1,…,c1,l-1,…,cm-1,0,cm-1,1,…,cm-1,l-1)∈C
如果存在最小的正整数l,使得向量
Tl(c)=
(λcm-1,0,λcm-1,1,…,λcm-1,l-1,c0,0,c0,1,…,c0,l-1,c1,0,c1,1,…,c1,l-1,…,cm-2,0,cm-2,1,…,cm-2,l-1)∈C
我们就说,C是Fq上码长为n,指标为l的λ-QT码,这里T是λ-常循环移位算子.显然,l是n的一个因子,令n=ml.
满足
ρ(c0,0,c0,1,…,c0,l-1,c1,0,c1,1,…,c1,l-1,…,cm-1,0,cm-1,1,…,cm-1,l-1)=(c0(x),c1(x),…,cl-1(x)).
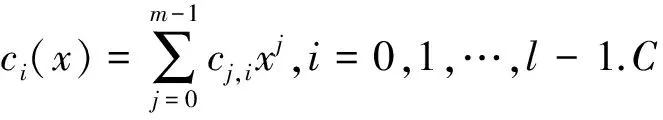
为了进一步研究λ-QT码,我们需要研究多项式xm-λ在有限域Fq上的分解.

xm-λ=(xt-α)pa.
令xt-α=f1(x)f2(x)…fk(x),其中f1(x),f2(x),…,fk(x)是Fq上的不可约多项式,那么
xm-λ=f1(x)paf2(x)pa…fk(x)pa.
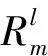
2 主要结果及其证明
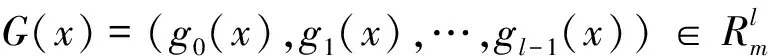
g(x)=gcd(G(x),xn-λ)=gcd(g0(x),g1(x),…,gl-1(x),xn-λ).
称为C的生成多项式. 进一步,若h(x)是使得h(x)g(x)=0成立的次数最低的首一多项式,则称h(x)为C的校验多项式,并且g(x)和h(x)是唯一的.
如果g(x)和h(x)分别是λ-QT码的生成多项式和校验多项式,则xn-λ=g(x)h(x).且
dim(C)=degh(x).
令
g(x)=f1(x)pa-i1f2(x)pa-i2…fk(x)pa-ik.
那么
h(x)=f(x)1i1f2(x)i2…fk(x)ik.
其中0≤i1,i2,…,ik≤pa.
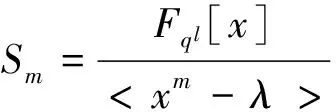

其中集合{α0,α1,…,αl-1}为FqL的一组Fq-基.
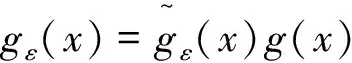
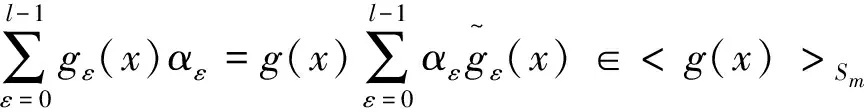
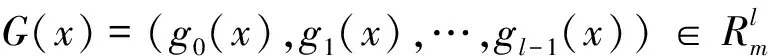

(2)h(x)是C的校验多项式当且仅当gcd(θ(x),h(x))=1.
(3)令G=(
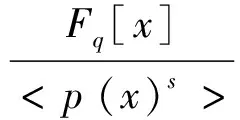
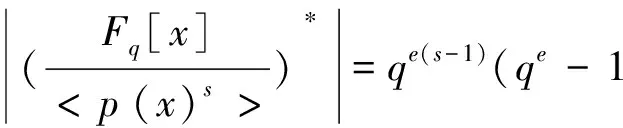
通过引理1和引理2,我们给出有限域上任意长度的具有相同校验多项式的不同的1-生成元λ-QT的计数公式.
定理1 令A是Fq上码长为n,指标为l的所有不同1-生成元λ-QT码组成的集合.设集合A中的λ-QT码的校验多项式为h(x).令h(x)=f(x)1i1f2(x)i2…fk(x)ik,其中fj(x)是Fq上次数为ej的不可约多项式,j=1,2,…,k.则
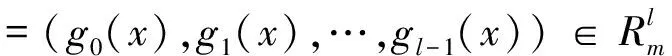


并且

由引理2,我们有
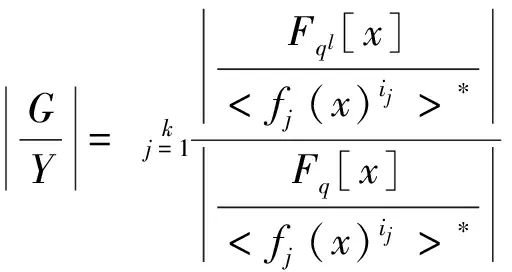
因此
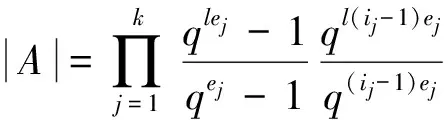
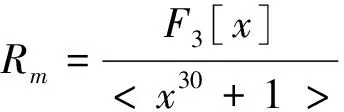
g0(x)=x14+x13+2x11+x10+x4+x3+2x+1.
g1(x)=x15+x14+2x12+x11+x5+x4+2x2+x.
g2(x)=x16+x15+2x13+x12+x6+x5+2x3+x2.
则
gcd(G(x),x30+1)=(x2+1)(x4+x3+2x+1)2(x4+2x3+x+1),
其中C的校验多项式h(x)为
h(x)=(x2+1)2(x4+x3+2x+1)(x4+2x3+x+1)2.
令A是F3上所有码长为90,指标为3并以h(x)为校验多项式的不同的1-生成元2-QT码构成的集合,则
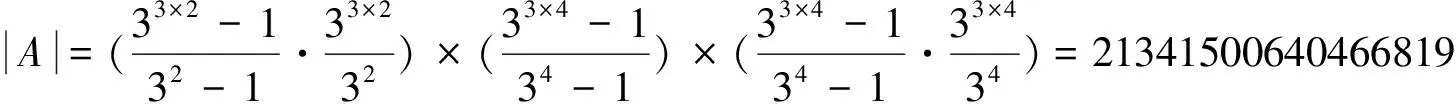
[1]LINGS,SOLÉP.Onthealgebraicstructureofquasi-cycliccodesI:finitefields[J].IEEETransactionsonInformationTheory, 2001,47(7) :2 751-2 760 .
[2]GULLIVERTA,BHARGAVAVK.Twonewrate2/pbinaryquasi-cycliccodes[J].IEEETransactionsonInformationTheory,1994,40(5):1 667-1 668.
[3]ESMAEILIM,GULLIVERTA,SECORDNP,etal.Alinkbetweenquasi-cycliccodesandconvolutionalcodes[J].IEEETransactionsonInformationTheory. 1998,44(1):431-435.
[4]GAOJ,FUFW.Noteonquasi-twistedcodesandanapplication[J].JournalofAppliedMathematicsComputing2015, 47(1):487-506.
[5]JIAY.Onquasi-twistedcodesoverfinitefields[J].FiniteFieldsandTheirApplications, 2012,18(2):237-257 .
[6]WANZX.LecturesonFiniteFieldsandGaloisRings[M]. [s.l.]:WorldScientific, 2003.
(编辑:姚佳良)
Enumeration of a class of one generator quasi-twisted codes over finite fields
LYU Jing-jie
(School of Science, Shandong University of Technology, Zibo 255049, China)
When the idexlofquasi-cycliccodesiscoprimewiththeextensiondegreeLofthefinitefieldFq,theenumeratorofdifferentonegeneratorquasi-twisted(QT)codesofarbitrarylengthwithafixedparity-checkpolynomialoverfinitefieldsisgiven.Wedefineabijectionamongsets,andresolvetheenumeratorofonegeneratorquasi-twistedcodesoverfinitefieldsindirectly.
one generator quasi-twisted codes; arbitrary length; enumeration.
2016-03-30
吕京杰,男,18353363182@163.com
1672-6197(2017)02-0049-04
TN
A
