基于和声搜索算法的软件可靠性模型参数估计方法

周园园，钱 丽，李敬明

(1.安徽广播电视大学省直分校 技术中心，安徽 合肥 230001；2.安徽新华学院 信息工程学院, 安徽 合肥 230088)

基于和声搜索算法的软件可靠性模型参数估计方法

周园园1，钱 丽2，李敬明2

(1.安徽广播电视大学省直分校 技术中心，安徽 合肥 230001；2.安徽新华学院 信息工程学院, 安徽 合肥 230088)

针对软件可靠性模型中参数估计不精确的问题，提出了一种基于和声搜索算法的软件可靠性模型参数估计方法.为了避免和声搜索算法在求解参数时陷入局部最优解，对算法作了改进：在和声记忆库初始化时采用反向学习策略，提高了收敛速度；利用全局信息产生新解，提高了全局搜索能力.使用该方法对5组数据的两个软件可靠性模型的参数进行了估计，实验结果表明，本算法应用于参数估计具有可行性和有效性，在精度和算法的收敛性上，明显优于其他智能算法.

软件可靠性模型；和声搜索算法；参数估计

随着软件规模日益扩大，人们对软件可靠性也越来越重视.软件可靠性模型就是采用统计知识对软件实际使用中收集的或软件测试中的失效数据进行分析，找出规律，建立一个参数模型，然后在软件可靠性数据的基础上对模型中的未知参数进行估计，最后用此模型对软件的可靠性进行定量估计或评价，从而开发出可靠的软件[1]. 参数估计是软件可靠性预测中最重要的一部分，参数估值结果的准确性决定了软件产品的可靠性评估结果的准确性.但是目前的软件可靠性模型大部分是非线性函数模型，其参数较难以估计.估计模型中参数的方法有很多，传统的有极大似然法、最小二乘法和贝叶斯法. 目前较新的参数估计方法是采用智能优化算法. 马敏书等利用遗传算法求解可靠性模型中的参数[2]，但该方法结构较复杂，精确度很低；张克涵等利用粒子群算法求解可靠性模型的参数[3]，该方法计算的结果精确度较高，但搜索范围大，收敛速度慢；郑长友等利用蚁群算法求解可靠性模型的参数[4]，该算法虽收敛速度较快，但精确度有待提高.因此，需要寻求一种更好的算法. 和声搜索(HarmonySearch，HS)算法是一种新的智能优化算法，该算法简单通用，易于与其他算法混合，构造出具有更优性能的算法从而更好地解决函数优化问题.有关研究表明,在解决多维函数优化问题上HS算法比遗传算法、模拟退火算法等具有更好的优化性能[5-8]. 因此，将该算法应用到软件可靠性模型的参数估计中是可行的.

1 软件可靠性模型

目前软件可靠性模型有100多种，其中使用最多的是GO模型和MO模型，这两个模型在预测的可靠性方面比较好.GO模型属于指数软件可靠性模型，MO模型属于非齐次泊松过程模型，它们代表了大部分的软件可靠性模型.本文研究的是GO模型和MO模型，它们的均值函数形式如下[9]：

GO模型：

μ(t)=a(1-e-bt)

(1)

MO模型：

μ(t)=ln(λ0θt+1)/θ

(2)

式中：μ(t)表示截止到t时刻检测到错误数的期望值；t表示错误发现的时刻；a,b,λ0,θ为未知参数.

2 和声搜索算法

2.1 标准和声搜索算法(HS)

HS算法模拟音乐演奏家创作的过程，在创作过程中音乐家不断地调整所奏乐器的音调，使整个演奏过程达到最佳状态.HS算法中将乐器、乐器的音调、和声、和声效果评价与组合优化问题中的决策变量、决策变量的值、决策变量组成的解向量、目标函数的适应度值进行类比. 具体的算法步骤如下[8]：

(1)初始化算法参数

初始化算法参数包括：决策变量的个数N；和声记忆库的大小HMS;各个决策变量的取值范围[Li,Ui];和声记忆库考虑概率HMCR;音调微调概率PAR;音调微调带宽BW;算法的迭代次数NI.

(2)初始化和声记忆库HM

随机生成HMS个和声x1，x2，…，xHMS存入和声记忆库HM作为优化问题的初始解.

和声记忆库中的每个音调(即决策变量)按照式(3)产生：

(3)

式中，i=1,2,…,HMS；j=1,2,…,N；Li和Ui分别是j分量值域的下界和上界；

(3)产生一个新的和声

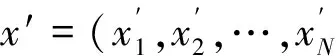
首先，考虑和声记忆库或者随机产生音调，公式如(4)式：

(4)

(5)

(4)更新和声记忆库HM

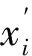
(5)检查算法终止条件

重复步骤(3)和步骤(4)，直到创作( 迭代) 次数达到NI为止.

2.2 改进的和声搜索算法

针对标准HS算法在后期收敛速度较慢和容易陷入局部最优解的问题，本文对标准HS算法做了如下两点改进：

(1)和声记忆库初始化的改进

反向学习策略已经被证明能产生高质量的初始解[10]，提高算法的收敛速度，而且已经被成功地应用到其他智能算法的解空间的初始化中.

为了提高初始解的质量，本算法不再按照标准的HS算法采用均匀分布的策略，而是采用均匀分布与反向学习相结合的策略对和声记忆库初始化. 和声记忆库中一半的解按照均匀分布策略产生如式(3)，剩余的一半解采用反向学习策略产生如式(6).

(6)

式中，k=HMS/2+1,…,HMS.

(2)新解产生的改进

为了提高算法的全局搜索能力，避免算法陷入局部最优解，在产生新解的步骤中，保留当前和声记忆库中的最优解，对标准HS算法中的式(5)做了改进，若新解来自于和声记忆库，有一半的概率是来自最优解，新解不再按照式(5)产生，而是按照式(7)产生：

(7)

式中，i=1,2,…,n；k=1,2,…,HMS,即将当前和声记忆库中最优解的第j维变量赋值给新解的第j维变量.

改进的HS算法流程与标准HS算法流程相同.

3 基于和声搜索算法的软件可靠性模型参数估计方法

3.1 算法流程

对两个模型中参数估计就是如何确定式(1)中a和b的值，式(2)中λ0和θ的值，使得每个模型的均值函数曲线更接近于实测数据曲线.

目标函数的构造是利用HS算法估计软件可靠性模型参数的关键，它是最优解的评价标准，借鉴文献[3]，本文采用式(8)作为目标函数，即

(8)

式中:T表示测试终止时间；m(t)表示累计到t时刻实际测试出来的软件失效数;μ(t)表示模型的均值函数;J表示模型估计的软件失效数与实际测试出的软件失效数之间的欧氏距离，其大小可以表示模型预测的精确度，J值越小，参数估计越准确，模型越精确.

利用HS算法估计参数时，首先预估每个式子中的未知参数的个数即HS算法中变量的个数，式(1)和(2)变量个数都是2；然后给出未知参数取值范围即HS算法中变量的值域；最后将文献[11]的实际数据集作为m(t)的数据，使用HS算法求解软件可靠性模型的均值函数的未知参数.具体算法流程如图1所示.

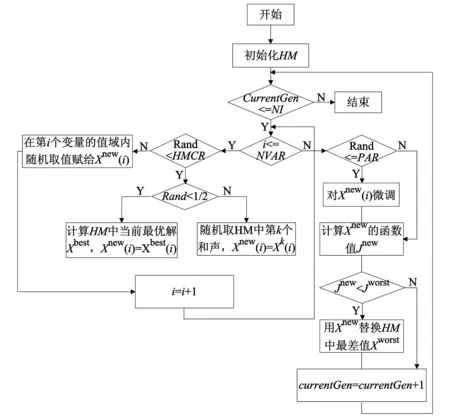
图1 算法流程图

3.2 仿真实验

采用Matlab2013使用改进后的HS算法，对Musa数据集[11]中的SYS1、SYS2、CSR1、CSR2、SS3 5组数据进行实验. 实验中HS算法中参数设置为HMS=5,HMCR=0.95，PARmin= 0.01，PARmax=0.99，BWmin=0.000 001，BWmax=(Ui-Li)/20，NI=50 000. 算法独立运行20次，取目标函数J的最小值所对应的参数.参数估计的精确度根据目标函数评价，目标函数值J越小，说明参数估计的精确度越高.

表1和表2给出了用5组数据估计两个可靠性模型参数的实验结果.结果表明了HS搜索算法应用于参数估计的可行性. 表3给出了粒子群(PSO)算法、蚁群算法和本文的HS算法参数拟合的结果.图2～图8则给出了两种模型分别拟合5组数据的曲线.

表1 G-O模型参数估计结果

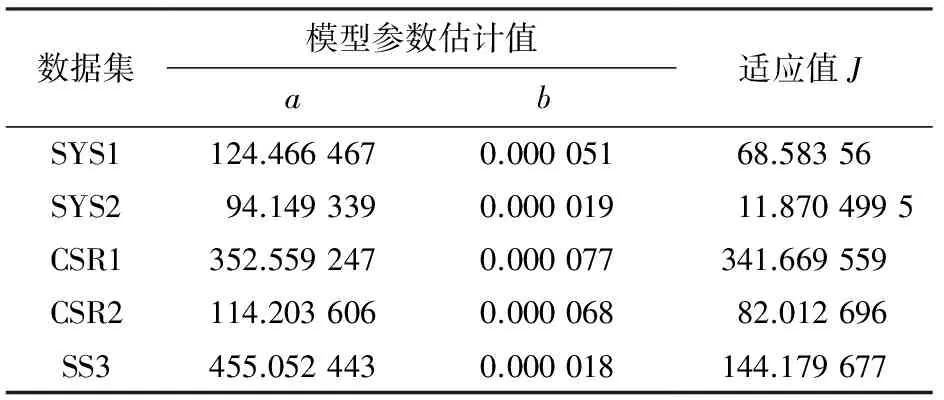
数据集模型参数估计值ab适应值JSYS1124．4664670．00005168．58356SYS294．1493390．00001911．8704995CSR1352．5592470．000077341．669559CSR2114．2036060．00006882．012696SS3455．0524430．000018144．179677

表2 M-O模型参数估计结果

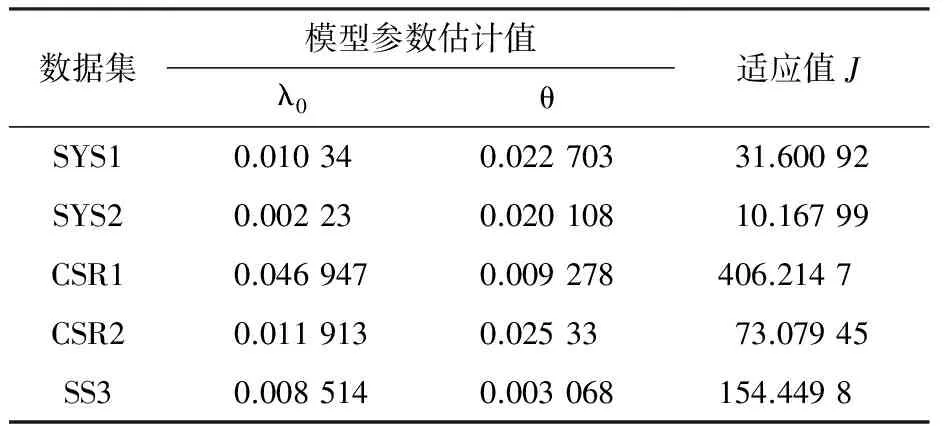
数据集模型参数估计值λ0θ适应值JSYS10．010340．02270331．60092SYS20．002230．02010810．16799CSR10．0469470．009278406．2147CSR20．0119130．0253373．07945SS30．0085140．003068154．4498

表3 PSO、蚁群算法和HS算法参数拟合的结果

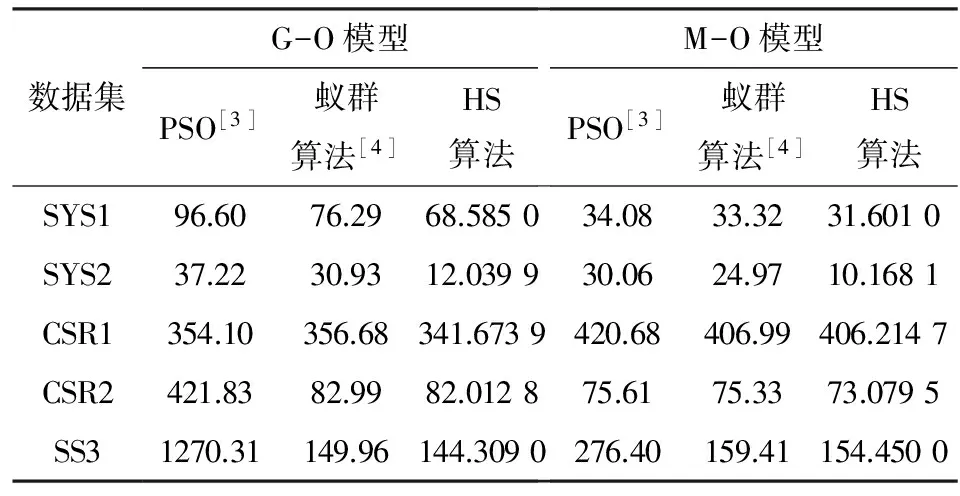
数据集G-O模型M-O模型PSO[3]蚁群算法[4]HS算法PSO[3]蚁群算法[4]HS算法SYS196．6076．2968．585034．0833．3231．6010SYS237．2230．9312．039930．0624．9710．1681CSR1354．10356．68341．6739420．68406．99406．2147CSR2421．8382．9982．012875．6175．3373．0795SS31270．31149．96144．3090276．40159．41154．4500

3.3 结果分析

(1)与PSO算法、蚁群算法的比较

由表1～表3和图2～图6可见, 本文提出的软件可靠性模型参数估计方法效果比较好，没有拟合不出来的情况，说明该算法对不同软件可靠性模型的适应性也比较好.从表3中可以看出，本文的方法得出的精度明显比PSO和蚁群算法的精度高.

图2 SYS1数据的拟合结果

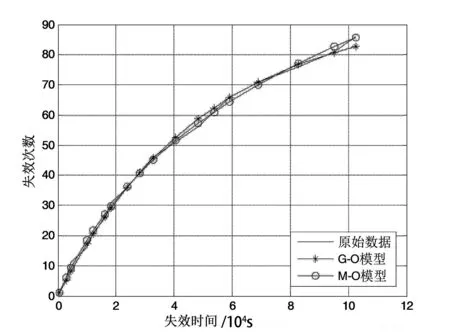
图3 SYS2数据的拟合结果

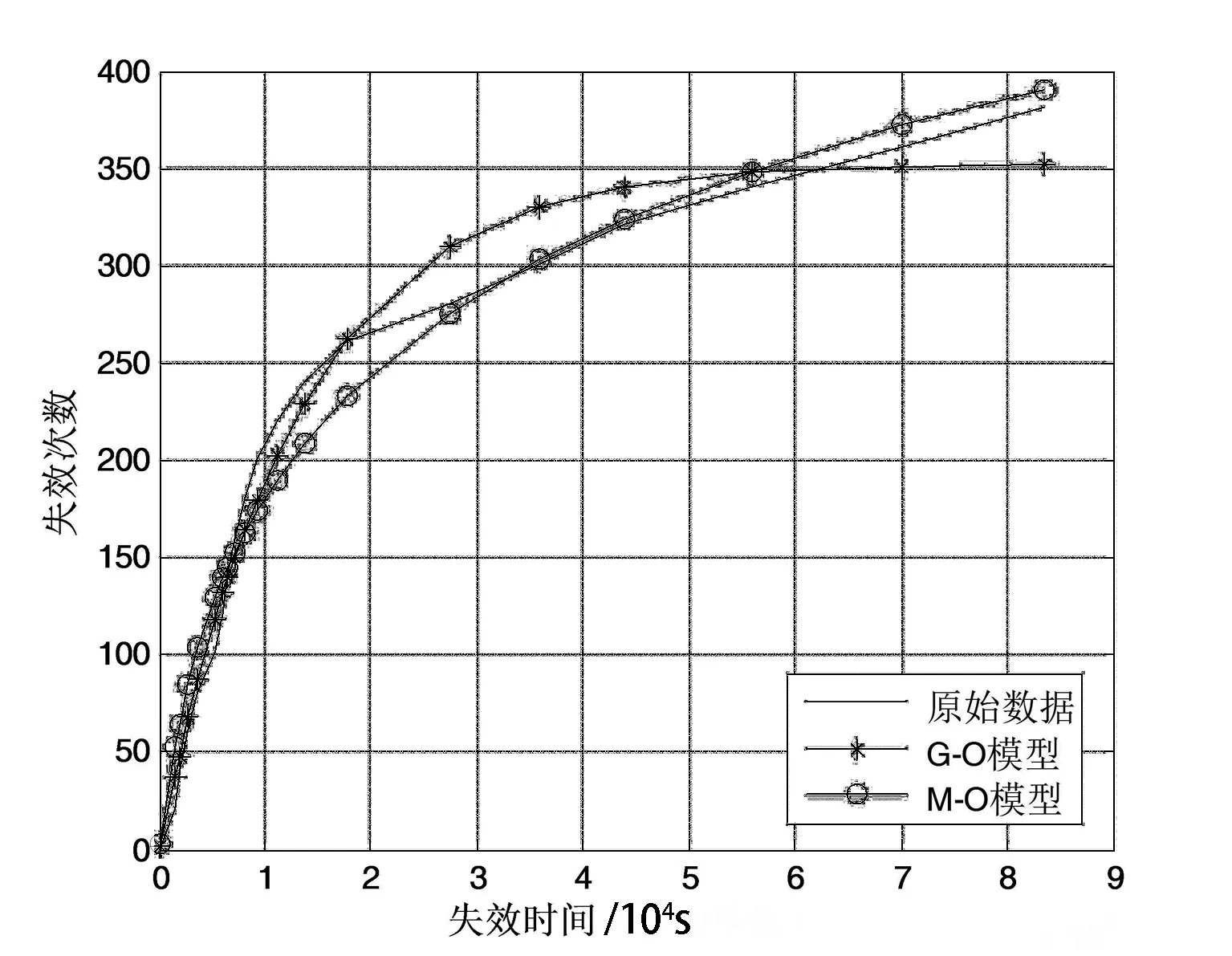
图4 CRS1数据的拟合结果

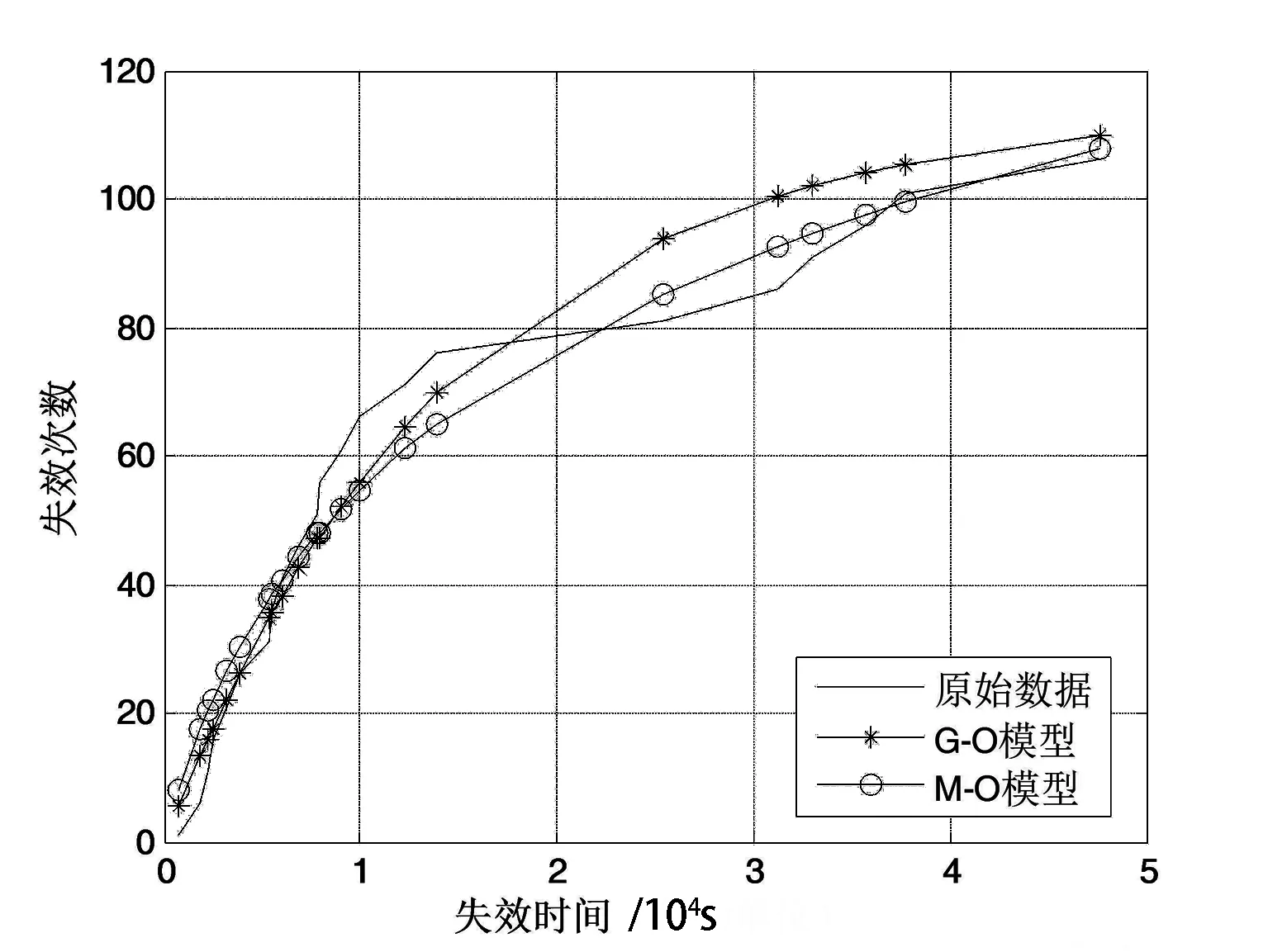
图5 CRS2数据的拟合结果

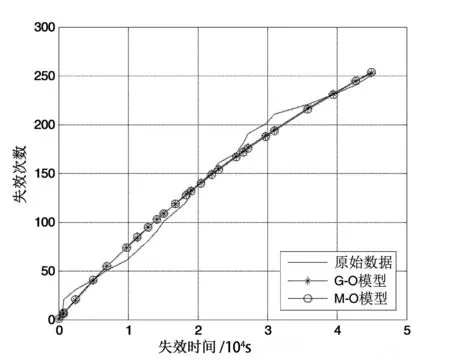
图6 SS3数据的拟合结果

(2)与其他HS方法的比较

图7给出了HS、IHS和IGHS 3种算法以SYS1数据集为测试数据求解GO模型优化的收敛曲线(限于篇幅，未给出其他模型优化收敛曲线)，比较了3种算法的收敛速度，横坐标表示迭代次数，每迭代1 000次保留一次最优值，纵坐标取最优值的以2为底的对数表示.从图7可以看出，改进算法的初始解的质量较高，在前3 000次迭代曲线相差不大，表明3种算法都能较快收敛，在8 000次时本文算法已趋于收敛，12 000次后HS和IHS算法才趋于收敛，这表明本文算法的收敛速度比HS，IHS的更快，其中IHS收敛速度是最慢的，这表明仅仅按照线性的调整参数未必能改善HS的性能.

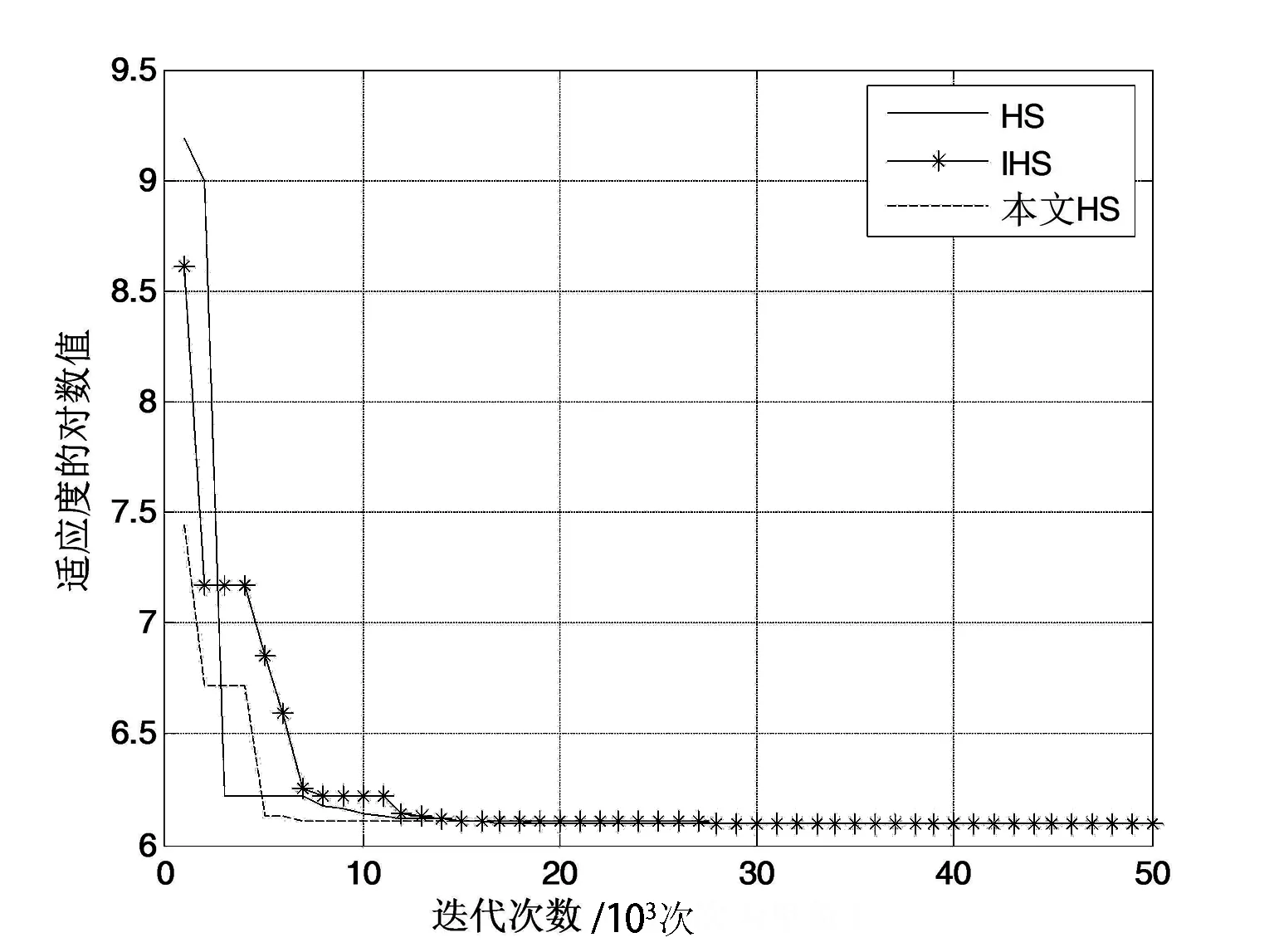
图7 3种HS算法的收敛曲线

4 结束语

针对估计软件可靠性模型中的参数不精确问题，提出一种改进的和声搜索算法用于估计软件可靠性模型参数.该算法采用反向学习策略初始化和声记忆库，并利用当前和声记忆库的最优解产生新解来改进算法. 使用该方法分别估计了Musa数据集中的5组数据的两种软件可靠性模型，通过实验验证了和声搜索算法在参数估计应用中的可行性和有效性.通过与其他智能算法比较可知，该算法参数估计的精度高、收敛速度快，能适应不同的模型.

[1]陆民演. 软件可靠性工程[M]. 北京: 国防工程出版社, 2011.

[2] 马敏书, 张仲义, 吕永波. 利用遗传算法进行软件可靠性增长模型参数估计[J]. 中国安全科学学报, 2004, 14(7): 9-12.

[3] 张克涵, 李爱国, 宋保维. 基于 PSO 的软件可靠性模型参数估计方法[J]. 计算机工程与应用, 2008, 44(11): 47-49.

[4] 郑长友, 刘晓明, 黄松. 基于蚁群算法的软件可靠性模型参数估计方法[J]. 计算机应用, 2012, 32(04): 1 147-1 151.

[5] TUO S H, ZHANG J Y. A harmony search algorithm for high dimensional multimodal optimization problems[J]. Digital Signal Processing, 2015, 46 : 151-163 .

[6] EHSAN V, SAEED T, SHAHRAM M. An intelligent global harmony search approach to continuous optimization problems[J]. Applied Mathematics and Computation, 2014, 232 : 670-684.

[7] ASHRAFI S M, DARIANE A B. Performance evaluation of an improved harmony search algorithm for numerical optimization: Melody Search (MS)[J]. Engineering Applications of Artificial Intelligence, 2013, 26(4): 1 301-1 321.

[8] 雍龙泉.和声搜索算法研究进展[J]. 计算机系统应用, 2011, 20(7): 244-248.

[9] HOANG P. 系统软件可靠性[M].李璐炜,译.北京:国防工程出版社,2014:203-205.

[10] WANG H, WU Z, RAHNAMAYAN S, et al. Enhancing particle swarm optimization using generalized opposition-based learning[J]. Information Sciences, 2011, 181(20): 4 699-4 714.

[11] LYU M R.Handbook of software reliability engineering[M/OL].New York:IEEE.Computer Society Press,1996[2016-05-13]. http://www.cse.cuhk.edu.hk/～lyu/book/reliability/data.htm.

(编辑：郝秀清)

Estimatingparametersofsoftwarereliabilitymodelbyharmonysearchalgorithm

ZHOUYuan-yuan1,QIANLi2,LIJing-ming2

(1.TechnologyCenter,AnhuiShengzhiRadioandTVUniversity,Hefei230001,China;2.SchoolofInformationEngineering,AnhuiXinhuaUniversity,Hefei230088,China)

Astotheproblemofinaccurateestimationoftheparametersofsoftwarereliabilitymodel,amethodofestimatingparametersofsoftwarereliabilitymodelbasedontheharmonysearchalgorithmisproposedinthispaper.Inordertoavoidtheharmonysearchalgorithmforsolvingtheparametersintoalocaloptimalsolution,twoimprovementsaremade.Firstly,theopposition-basedlearningisusedtoinitializedharmonymemorytoimprovethespeedofconvergence.Secondly,globalinformationisusedtogeneratethenewtoimprovetheglobalsearchability.Theparametersoftwosoftwarereliabilitymodelsofsevendatasetswereestimatedbytheproposedmethod.Theexperimentalresultsshowthatthealgorithmisfeasibilityandeffectivenessinparameterestimationandissuperiortoothermeta-heuristicalgorithmsintheconvergenceandaccuracy.

softwarereliabilitymodel;harmonysearchalgorithm;parameterestimation

2016-05-18

安徽省教育厅自然科学基金重点项目(KJ2014A100,KJ2016A308)

周园园, 女,yuanyzhou@qq.com

1672-6197(2017)02-0044-05

TP301.6

A