3-RCR并联机构结构参数综合优化设计

陈海真，魏 峥，李爱军，王红梅,毛立云

(1.山东理工大学 机械工程学院，山东 淄博 255049；2.山东省水利技师学院 基础部，山东 淄博 255130)

3-RCR并联机构结构参数综合优化设计

陈海真1，魏 峥1，李爱军1，王红梅1,毛立云2

(1.山东理工大学 机械工程学院，山东 淄博 255049；2.山东省水利技师学院 基础部，山东 淄博 255130)

少自由度并联机构优化设计的理论研究虽然取得了一定的成果，但其推广应用仍受到限制.对3-RCR并联机构位置进行了求解，得到了其雅可比矩阵，并获得了机构工作空间的体积和全域条件数；以此为基础对机构进行了参数综合优化，以工作空间的体积最大和灵巧度最高为目标，建立了优化设计数学模型，并用MATLAB遗传算法优化工具箱求解，得到了满足目标要求的结果，为机构的推广应用提供了理论基础.

三平移并联机构；灵巧度；工作空间；工程遗传算法；结构参数优化

目前，对少自由度并联机器人机构优化设计的理论研究取得了一定的成果，但以增大工作空间或者是单纯提高灵巧度为单目标进行优化的居多，以多目标进行优化设计的还较少，因此并联机器人机构不能得到很好的推广应用. 并联机构优化设计数学模型特点之一是多维非线性，因此如何采用一种有效的算法进行全局并行搜索，实现多个目标综合考虑来寻求结构参数的最优值是人们一直致力研究的目标.本文基于3-RCR并联机构的工作空间体积和全域条件数，以工作空间和灵巧度[1-2]为目标，利用工程遗传算法求解，对其结构参数进行综合优化设计.

1 机构描述

图1所示为3-RCR并联机构的结构简图，此并联机构由动平台、静平台、3个结构相同的支链(RCR)组成.动平台和静平台都是正三角形而且相互平行，3条支链将动静平台相连，3条支链所在的平面都与上下动、静平台垂直，并且同时与三角形平台相应的边垂直，每条支链中的C副和两个R副轴线都与三角形平台的相应边平行，3条支链呈120°度对称布置.

图1 并联机构结构简图

2 机构的位置解及雅可比矩阵

2.1 位置正反解

建立如图1所示坐标系A1-XYZ，X轴与EF重合，Y轴与EF垂直，据右手法则确定Z轴的方向垂直向上.机构的相关参数如下：静、动平台都是等边三角形，边长分别是a、b；连杆AiBi(i=1,2,3)的长度是l1，并且与竖直方向的夹角分别为i(i=1,2,3)；连杆BiCi(i=1,2,3)的长度是l2，且与水平方向的夹角各为βi(i=1,2,3)；支链AiBiCi(i=1,2,3)中圆柱副中心的位移分别是di(i=1,2,3).

2.1.1 位置反解

机构的位置反解，即已知动平台上点D的输出参数(XD,YD,ZD),求解支链的输入参数αi(i=1,2,3)[3].动平台作三维平移，其上各点具有相同运动情况，因此可以从动平台上任选一点对其运动进行分析，本文选动平台几何中心点D进行分析. 通过每条支链末端的转动副将运动输入i(i=1,2,3)最终传递给动平台，位置反解可以根据D点与各转动副中心点Ci(i=1,2,3)的空间位置关系来建立.

在坐标系A1-XYZ中，设点Ci(i=1,2,3)、D的空间坐标依次是: (Xci,Yci,Zci) (i=1,2,3) 、(XD,YD,ZD)，各坐标之间有如下关系：

(1)

在坐标系A1-XYZ中，点Ci(i=1,2,3)的坐标分别为

(2)

(3)

(4)

由式(1)、式(2)可得

(5)

将式(5)中的后两式取平方和消去中间变量β1，得

(6)

同理，由式(1)、式(3)可分别求得

(7)

(8)

式中：

2.1.2 位置正解

由式(5)后两式可得

(9)

同理，由式(1)、式(3)和式(4)、可分别求得

(10)

(11)

用Newton-Raphson方法可以对以上三元二次方程组进行求解.

2.2 机构的雅可比矩阵

式(9)～式(11)为3-RCR并联机构输入和输出之间的函数关系式，要求解主动关节输入速度与动平台输出速度的关系，可以将式两端分别对时间求导[4-5],即

(12)

式中，J-1为速度雅克比矩阵的逆矩阵，且

J-1=

(13)

如果det(J-1)≠0，则

(14)

式中，J为机构速度雅克比矩阵[4-5].

3 机构工作空间的体积和全域条件数

3.1 工作空间的体积

图2为工作空间截面示意图.对工作空间进行边界搜索[6]，然后用与平面XY平行的平面将工作空间分割成若干个微分子空间，微分子空间的厚度为ΔZ.如果ΔZ足够小，这些微分子空间可以近似被看作是高度为ΔZ的柱体，机构工作空间的体积近似等于这些子空间体积的累加.

根据机构的位置反解不难看出机构的工作空间截面是单域的，因此机构工作空间的体积可表示为[3]

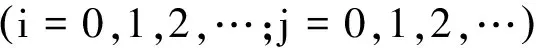
(15)

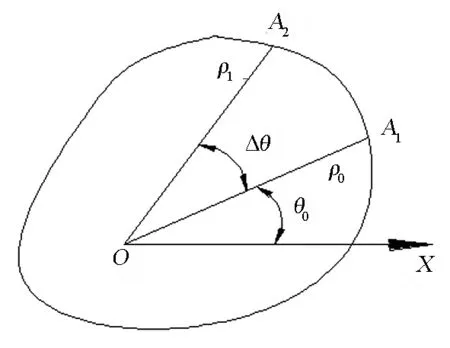
图2 工作空间截面示意图

工作空间搜索程序根据机构的位置反解编写，并结合式(15)可计算出工作空间的体积.

3.2 机构的全域条件数

用局部条件数衡量机构在某一位置的运动灵巧度，其定义为

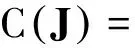
(16)

式中：J是机构的雅可比矩阵；C为条件数，其范围为1≤C≤.当条件数C的值接近1，雅可比矩阵J是良态矩阵；当条件数C=1，机构的运动传递性能最佳，机构的这一形位被称为运动学各向同性；如果条件数C无穷大，机构的雅可比矩阵J为病态，机构处于特殊形位.

机构在给定工作空间内的总体运动性能用全域条件数来表示[4]，全域条件数可作为衡量机构运动性能指标的工具，若G为全域条件数，则

(17)

式中，W为机构的工作空间容积.将条件数C代入式，可得出G的值域.当全域条件数G接近于0，表明有坏的全域条件数，机构的运动性能较差；反之，全域条件数G接近于1，表明有好的全域条件数，机构运动性能较好，而且G越接近于1，机构在给定空间内的总体运动性能越好.但是因为一般较难得到全域条件数G的解析解，或者有解析解但其表达式也十分复杂，所以全域条件数G一般用离散型表示，即

(18)

式中：∑(1/C)为工作空间网格内的每一个条件数倒数的累加；w为落在工作空间网格内点的数量.对于非离散型和离散型全域条件数的值域意义相同.w与机构的工作空间容积W相对应，分子与满足工作空间约束条件的点的条件数倒数的积分相对应，用极坐标搜索算法来求取工作空间G的值时，式(18)可以作为机构优化的目标函数.

4 机构结构参数综合优化

为使并联机构有更大的工作空间和更好的灵巧性，必须对其进行结构参数综合优化[7-8].优化方法采用多目标优化方法中的主目标函数法，以灵巧度为主目标函数，将子目标工作空间转化为新的约束条件，并将工作空间子目标限制在一定的范围内.运用遗传算法进行求解.设G为主要目标函数，则待优化的函数可以表示为

(19)

为了计算简单，对结构参数变量进行处理，给出尺寸约束范围为

由前面工作空间优化分析对工作空间体积约束可确定为：11≤V≤14.灵巧度函数用MAT LAB中的M文件编写，利用MATLAB遗传工具箱求机构的最优解[9].

此并联机构结构参数优化前后在同一工作空间截面上的灵巧度图谱如图3、图4所示；优化前后机构的工作空间三维图如图5、图6所示.

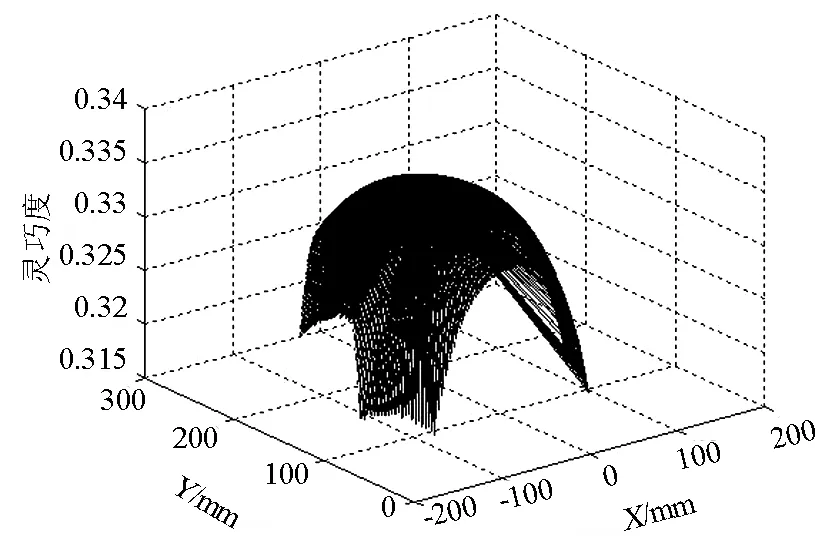
图3 优化前截面Z=300mm上的灵巧度

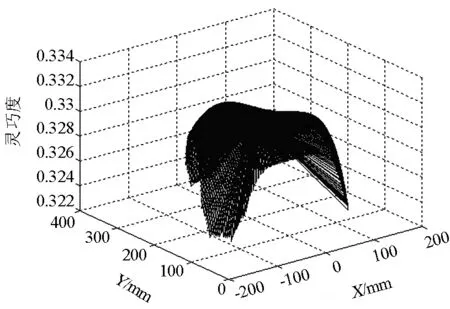
图4 优化后截面Z=300mm上的灵巧度

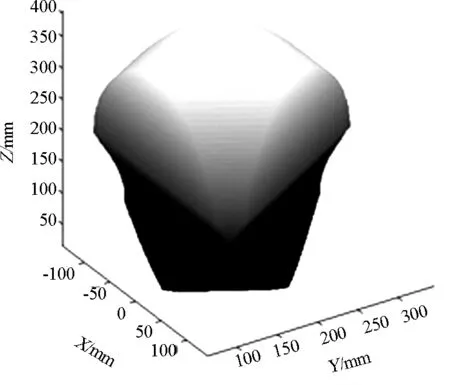
图5 优化前机构的工作空间三维图

由图3和图4看出，由于各截面所处的位置不同，各个截面上的灵巧度在优化前后有所变化，优化后截面边界处的灵巧度有所提高，中心处的灵巧度与边界处的灵巧度差值变小了，即优化后机构截面各处的运动性能波动变小了，机构有更加平稳的运动性能.由图5和图6看出，与优化前相比，多目标综合优化后的工作空间更加饱满.

图6 优化后机构的工作空间三维图

机构在给定工作空间内的灵巧度用全域条件数来表示，表1给出一组结构参数优化前后工作空间体积和全域条件数的值，由表1可进一步看出优化后机构工作空间和灵巧度的变化. 多目标优化后工作空间的体积相对增大了34.97%，全域条件数的值相对提高了7.4%，说明优化后此并联机构的总运动性能有所提高.

表 1 参数、工作空间体积和全域条件数初值及优化值

参数值参数/mmabl1l2工作空间体积/mm3全域条件数G优化前6003002002009．44×1060．2404优化后649．931290．960202．231241．011．274×1070．2582

5 结束语

采用主目标函数法对3-RCR并联机构结构参数进行了多目标综合优化，以工作空间和灵巧度为优化目标，运用MATLAB遗传工具箱计算得到了最优方案.用极坐标搜索法绘制出机构优化前后在某截面上的灵巧度图，通过与单目标优化灵巧度图对比可知，机构参数进行多目标综合优化后，其运动平稳性有所提高；优化后机构的工作空间变得更饱满，机构的综合性能显著提高.

[1] 高洪，蒋璇，肖平，等. 6-3-3并联机构尺度的优化综合[J].机械设计，2012，29(8)：57-60.

[2] YU Y,LIANG W Y. Design optimization for parallel mechanism using on human hip joint power assisting based on manipulability inclusive principle [C] //2012 IEEE International Conference on Robotics and Automation, 2012：2 306-2 312.

[3] 黄真．空间机构学[M]．北京：机械工业出版社，1991．

[4] 刘大炜，王立平. 基于工作空间的4RRR冗余并联机构支链优化[J].清华大学学报(自然科学版)，2010，50(8)：1 239-1 242.

[5] 杨明星，郭宗和，王德军， 等.一种新型4自由度并联机构的参数优化及其应用研究[J].机床与液压，2014，42 (15 ):15-18.

[6] 贾晓辉，刘今越 . 3-PRR柔性并联机构的优化设计机械设计[J].2014，31(1)：26-29.

[7] 王庚祥 ，刘宏昭，原大宁. 一种新型3-SPS/CR并联机构及其优化设计[J]. 机械科学与技术，2012，31(7)：1 094-1 099.

[8] KONG M X， CHEN L， DU Z J，et al . Multi-objective optimization on dynamic performance for a planar parallel mechanism with NSGA-II algorithm[J]. Jiqiren/Robot，2010，32(2):271-277.

[9] STORMY A. MATLAB编程与工程应用[M]. 鱼滨, 等, 译. 北京: 电子工业出版社, 2013.

(编辑：郝秀清)

Structural parameters multi-objective optimization design of 3-RCR parallel mechanism

CHEN Hai-zhen，WEI Zheng, LI Ai-jun, WANG Hong-mei, MAO Li-yun

(1.School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China；2. Basic Department， Normal School of Water Conservation Technology of Shandong University, Zibo 255130, China)

Some achievements have been obtained for structural parameter optimization design theoretical research of the less freedom parallel mechanism, but its spread application is still restricted. In this research, the 3-RCR position solutions are obtained, then Jacobin matrix of the structural is received. The workspace volume and global condition index are calculated through position analysis and solution of the Jacobin matrix．On this basis, structural parameters multi-objective optimization design are executed and the optimization mathematical model is established in order to get the largest workspace volume and the highest degree of dexterity．The mathematical model is solved by using the genetic algorithm toolbox of MATLAB．It provides the theoretical basis for the popularization and application of the mechanism.

three translation parallel mechanism；dexterity；workspace；engineering genetic algorithm; optimization of structural parameters

2016-05-11

陈海真,女,chhaizhen@163.com

1672-6197(2017)02-0035-05

TH

A