基于希尔伯特-黄变换和EMD消噪的电压闪变信号检测

1 基于HHT与EMD消噪的电压闪变检测方法

1.1 Hilbert变换

对于任意连续信号c(t)，经由Hilbert变换可以得到它的共轭信号:

(1)

其解析信号为

(2)

瞬时频率可表示为

(3)

1.2EMD算法

EMD分解是通过提取原始信号中固有模态函数IMF(IntrinsicModeFunction)，来揭示信号的故障特征.IMF应当满足a信号曲线的极值点数量与曲线本身穿过零点的次数要相等或者两者数量相差最大为一.b任意信号上一点，极大值组成的包络与极小值组成的包络，它们的平均值为0[5].

EMD对信号的具体处理过程如下[6-7]：

(1)任意给定信号X(t)，首先确定X(t)所有极值点，用三次样条插值曲线连接所有极大值形成上包络线，同理用三次样条插值曲线连接极小值可得下包络线.上下包络线的均值为m1

h1(t)=X(t)-m1

(4)

将h1(t)作为新的X(t)，重复上述的步骤，直到h1(t)满足IMF两个条件；此时的h1(t)为原始信号第一阶IMF，标记为C1.

(2)把C1从X(t)中剥离出来，就可以得到一个去除了高频分量的信号r1.

r1=X(t)-C1

(5)

将r1视作为“新信号”X(t)，重复步骤(1)，就可得到第二个IMF分量C2；然后不断重复这个过程可以得到C3到Cn，直到第n阶的rn是个单调的函数，此时再不会产生IMF分量.

rn(t)=rn-1-Cn

(6)

(3)X(t)可以表示为n个IMF分量与残余项之和，即

(7)

式中：rn(t)是残余量；Cj(t)是各个IMF分量，象征着由高到低不同频率段信号的成分.

1.3 EMD消噪

早先的EMD消噪方法通过直接删除噪声最多的几个IMF分量并将余下IMF分量进行重构，即得到消噪后信号.这种方法过于粗略，其结果往往误差严重.因此近年来EMD消噪都是对各IMF分量进行阈值滤波，然后再进行重构.文献[8]提出经验模态分解与小波阈值滤波相结合的方法.文献[9]提出一种基于自相关的EMD消噪方法，但是其消噪核心依然是小波变换.为了更便捷选取IMF分量的阈值，本文提出了一种基于噪声能量统计特性的EMD消噪方法.

假设含噪声的原始信号为S(t)=X(t)+n(t)，X(t)为原始无噪声信号，n(t)代表方差为δ2的白噪声信号.首先将S(t)进行经验模态分解，随后对各个IMF进行滤波处理.文献[10-11]对EMD分解与白噪声统计特性进行了研究得出结论：

(1)经过EMD分解的高斯白噪声在每个IMF分量里依然遵循高斯分布.其噪声能量如以下公式逐层递减：

(8)

式中Ek代表第k个IMF分量中含有高斯白噪声的能量，ε≈2.01，δ≈0.719.

(2)由于EMD分解产生的第一个IMF分量中满含高频噪声，该IMF中高斯白噪声分布的能量E1近似的等于该IMF的总能量.文献[10-11]定义能量公式，每一个样本点的能量等于该样本点值的平方.N为样本点数.

(9)

因此EMD消噪时，由于第一个IMF分量含有大量高频噪声，信号分解后该分量不再参与重构过程.随后对其余的IMF分量进行阈值消噪.由于软阈值去噪后的信号与实际信号存在偏差，因此选用硬阈值去噪，即

(10)

消噪时每个IMF分量中作为噪声被删除的能量应当等于估算的该IMF噪声能量.根据公式(8)与公式(9)即可求出各个IMF分量的噪声估计能量.然后将各个IMF分量样本点值的绝对值从小到大进行排序：

(11)

Cj(ti),i=1,2,3…n,i表示第j个IMF分量采样点经过重新排列后所在的次序，第i项.

根据(10)式除第一个IMF分量外，每个IMF分量消噪时被删除的点的总能量应该近似等于公式(8)与公式(9)估算的噪声能量Ek，k=2,3…n.按照(式11)的排序结果，将已排序样本点的能量进行累加至如式(12)成立时

(12)

则对应的IMF的消噪阈值为

(13)

以上方法遵循能量近似对等的原则，依据各个IMF分量中样本点的值自适应确定各个IMF分量的消噪阈值，然后IMF分量对应相应的阈值按照(10)式进行消噪，最终得到S(t)消噪后信号

(14)

综上所述EMD消噪步骤如下：

(1)将带有噪声的原始信号进行经验模态分解，其结果如式(7)所示.

(2)采用公式(8)与公式(9)估算出各个IMF含有的噪声能量Ek.

(3)将各个IMF分量的采样点按照式(11)进行排序，然后按照式(12)进行累加确定各个IMF分量的消噪阈值.

(4)利用已经确定的各个IMF阈值对各个IMF进行硬阈值去噪，再利用式(14)重构消噪后的信号.

2 仿真与分析

闪变是因为电压波动引起的，电压波动的检测可看成单一频率的调幅波对工频载波(50Hz或60Hz)的调制[4]，其瞬时电压可以表示为

u(t)=A(1+mcos(Ωt))cos(ωt)

(15)

式中：A为工频载波的幅值；ω为工频载波的角频率；m为调幅波的幅值；Ω为调幅波的角频率.

2.1EMD消噪仿真对比

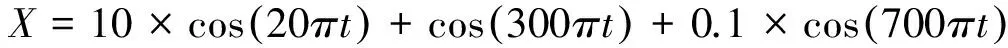
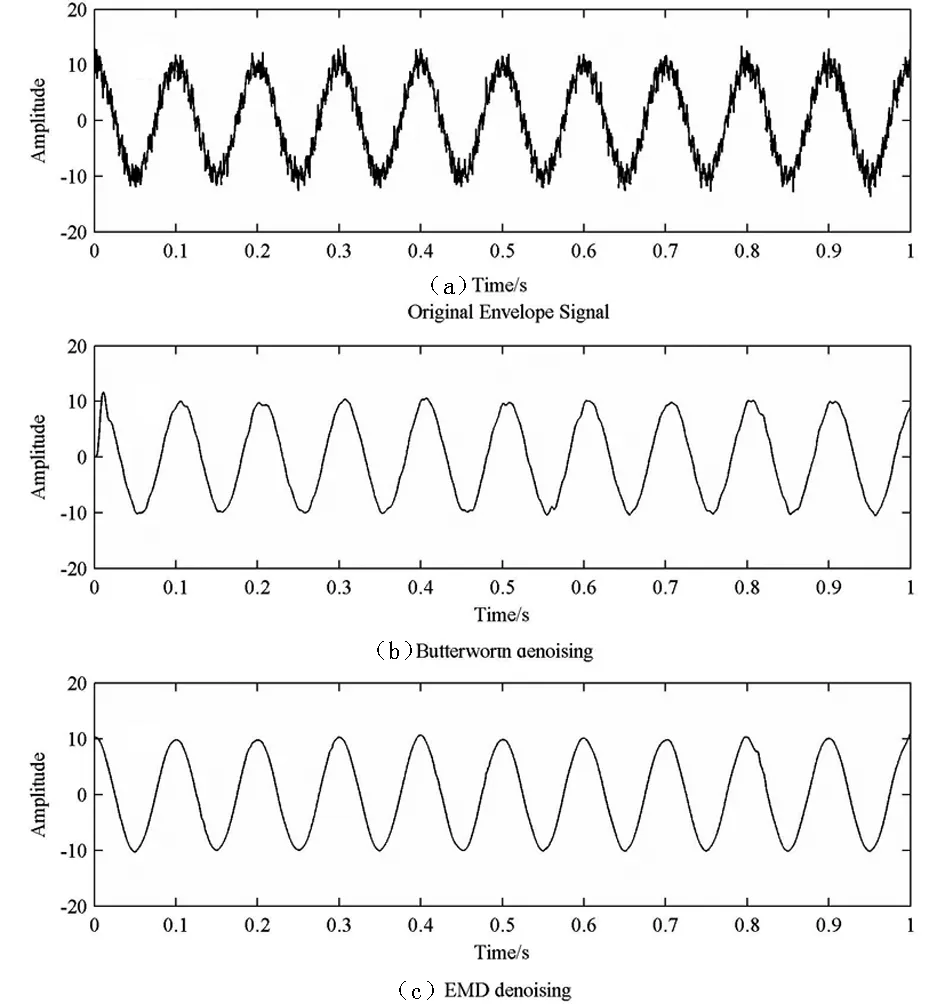
图1 消噪仿真对比图

由图1可知，图1(a)显示的是含噪声的原始信号，图1(b)显示噪声信号经由巴特沃兹消噪后的信号曲线，图1(c)显示的是噪声信号经由EMD消噪后的信号曲线.对比图1(a)于图1(b)可知，基于噪声能量统计特性的EMD硬阈值消噪方法对于噪声信号有着良好的消噪特性.

2.2 电压闪变的仿真与分析

分别采用IEC平方检测法、小波分解与同步检测法、希尔伯特-黄变换与EMD消噪相结合检测法对某一时刻发生的单频电压闪变、某一时刻发生的多频电压闪变进行仿真检测.对比三种方法提取电压闪变的图形与信息.

2.2.1 某一时刻发生单频电压闪变

1)某一时刻发生单频电压闪变可以表示为

(16)

表1 某一时刻发生电压闪变的信号仿真参数

相对幅值频率/Hz初始相位工频载波1500调幅波0．09110

假设采样的时间设置成2s，采样频率为3 200Hz.小波分解的小波基选为DB24，分解层数为6层.

2)信号仿真图像

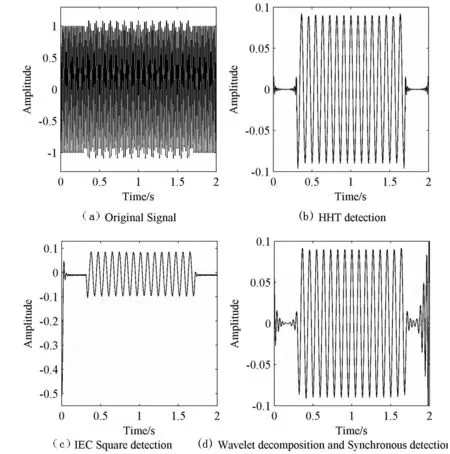
图2 某一时刻发生单频闪变信号的仿真结果

图2(a)是原始信号，假设该信号在某一时刻发生单一频率的闪变，图2(b)是采用基于希尔伯特-黄变换结合EMD去噪法提取的电压闪变调幅波信号.图2(c)显示为采用IEC推荐的平方检测法提取的调幅波信号.图2(d)显示的为采用基于小波的同步检测法提取的调幅波信号.对比以上图可知希尔伯特-黄变换与EMD消噪相结合的电压闪变检测法能够良好的提取电压闪变的调幅波而且采用新方法提取的调幅波在边界上比小波法提取的调幅波要好.

图3 原始信号时频图

由图3原始信号的时频图可知，发生电压闪变开始时间：开始是0.3s，结束是1.7s.

3)仿真结果分析

由于边界效应，在计算信号的参数时(幅值和频率)，波形两边均应去除两个周期，以保证测量的精度.三种检测方法仿真，得到的调幅波频率、幅值计算结果见表2.

表2 三种方法得到调幅波参数

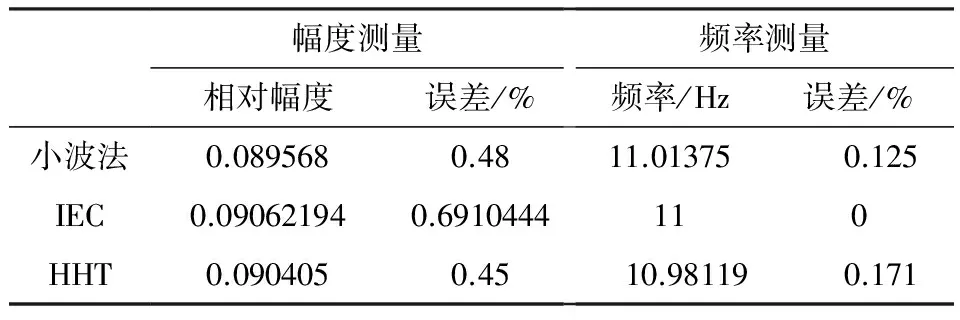
幅度测量频率测量相对幅度误差/%频率/Hz误差/%小波法0．0895680．4811．01375 0．125IEC0．090621940．6910444110HHT0．0904050．45 10．98119 0．171

由表2可知，三种检测方案得到调幅波相对幅度误差都不超过0.7%，得到的频率误差皆不超过0.2%.对于某一时刻发生的单频电压闪变而言，三种方案都有极好的检测效果.

2.2.2 某一时刻发生多频电压闪变

1)某一时刻发生多频电压闪变可以表示为

(17)

某一时刻发生多频电压闪变信号构造参数见下表3;仿真时在信号里添加信噪比为20的高斯白噪声.

表3 某一时刻发生多频电压闪变信号的仿真参数

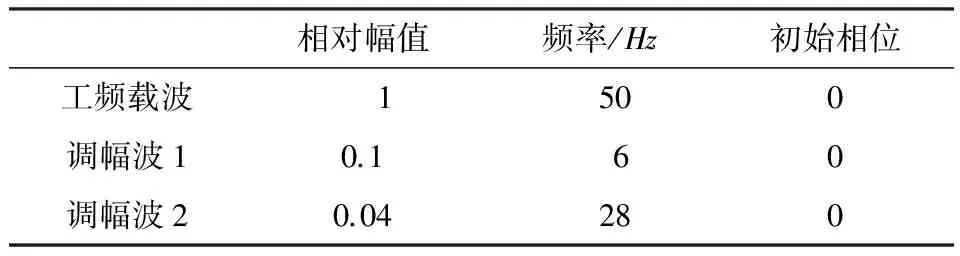
相对幅值频率/Hz初始相位工频载波 1 500调幅波10．1 60调幅波20．04 280

假设采样的时间设置成2s，采样频率为3 200Hz.小波分解的小波基选为DB24，分解层数为7层.

2)信号仿真图像

由于采用IEC平方检测法难以提取多频闪变信号中的各频率调幅波，因此某一时刻多频电压闪变仅取小波分解与同步检测法、基于希尔伯特-黄变换和EMD消噪的电压闪变检测法进行仿真.

图4 某一时刻发生多频闪变信号的仿真结果

图4(a)是原始信号，假设该信号在某一时刻发生多频率的闪变并伴有噪声.图4(b)显示的为消噪后的原始信号的时频图，由图4(b)可以看出电压闪变的时刻：开始是0.3s，结束是1.6s.图4(c)、(d)显示的分别为采用基于希尔伯特-黄变换与EMD消噪的检测法得到的较高频率调幅波信号与较低频率调幅波信号；图4(e)、(f)显示的分别为采用小波分解与同步检测法得到的较高频率调幅波信号和较低频率调幅波信号.对比图4(c)～4(f)可知，小波法对于多频电压闪变信号提取多少存在缺陷.

3)仿真结果分析

由于边界效应，在计算信号的参数时(幅值和频率)，波形两边均应去除两个周期，以保证测量的精度.两种检测方法仿真，得到的调幅波频率、幅值计算结果见表4、表5.

表4 两种方法提取高频率调幅波的计算参数

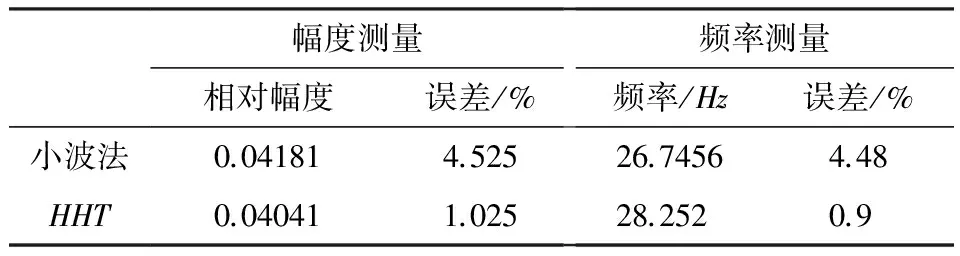
幅度测量频率测量相对幅度误差/%频率/Hz误差/%小波法0．041814．52526．74564．48HHT0．040411．02528．2520．9

表5 两种方法提取低频率调幅波的计算参数

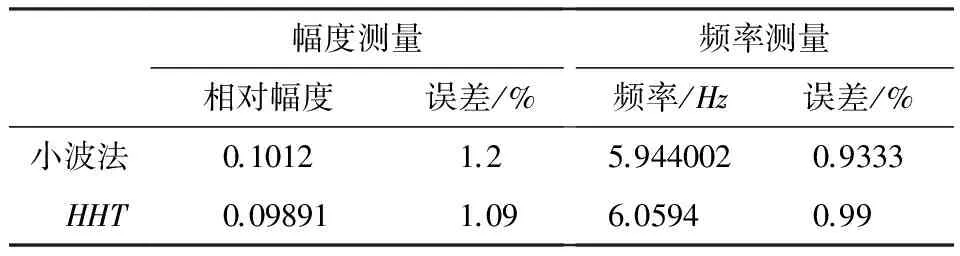
幅度测量频率测量相对幅度误差/%频率/Hz误差/%小波法0．10121．25．9440020．9333 HHT0．09891 1．096．05940．99

由表4、表5知，小波分解与同步检测法虽然能提取高频与低频调幅波，但提取的较高频率调幅波幅度、频率误差过大，不能很好的揭示电压闪变调幅波讯息；而基于希尔伯特-黄变换和EMD消噪的电压闪变检测方法能够精确的检测多频闪变信号的调幅波数据，提取的高频与低频调幅波数据误差<1.1%，其准确性优于小波分解与同步检测法.

3 结束语

针对突变性电压闪变现象，提出了基于希尔伯特-黄变换和EMD消噪的电压闪变检测方法.该方法首先利用希尔伯特-黄变换提取电压闪变信号的包络并进行EMD消噪，随后将消噪的包络信号进行经验模态分解，提取调幅波的特征信息，获得电压波动与闪变的发生及结束时刻.仿真结果表明，对于突变性的单频电压闪变，提取的调幅波幅值和频率的误差分别为0.45%和0.171%；对于突变性的多频电压闪变，提取的高频率调幅波幅值和频率的误差分别为1.025%和0.9%，提取的低频率调幅波幅值和频率的误差分别为1.09%和0.99% .因此，新方法能精确地检测出电压闪变信号的频率、幅值与时间，是一种电压闪变的有效检测方法.

[1]郭上华,黄纯,王磊,等. 电压波动和闪变的检测与控制方法[J]. 继电器, 2004, 32(3) : 45-48.

[2]TOIVONENL,MORSKYJ.Digitalmultiratealgorithmsformeasurementofvoltage,currentpowerandflicker[J].IEEETransonPowerDelivery, 1995, 10(1):116-126.

[3]堵俊,邵振国,郭晓丽,等. 用小波分析提取电压闪变的幅值调制信号[J]. 电力系统及其自动化学报, 2006,18 (3) : 34-37.

[4]LIZM,SHENJ,LIUW,et.Voltageflickermonitoringbasedonvirtualinstrumentandwaveletpackettransform[J].InternationalJournalofAdvancementsinComputingTechnology(IJACT), 2012, 23(4):466-474.

[5]杨永锋,吴亚锋. 经验模态分解在振动分析中的应用[M]. 北京: 国防工业出版社, 2013.

[6]刘志刚,李文帆,孙婉璐.Hilbert-Huang变换及其在电力系统中的应用[J]. 电力自动化设备, 2012, 32(4): 109-116.

[7]张杨,刘志刚.EEMD在电能质量扰动检测中的应用[J]. 电力自动化设备, 2011, 31(12): 86-91.

[8]陈卫萍,潘紫微. 基于经验模态分解的小波阈值滤波去噪[J]. 安徽工业大学学报(自然科学版), 2010, 27(4):397-400.

[9]席旭刚,武昊,罗志增. 基于EMD自相关的表面肌电信号消噪方法[J]. 仪器仪表学报, 2014, 35(11): 2 494-2 500.

[10]FLANDRINP,RILINGG,GONCALVESP.Empiricalmodedecompositionasaflickerbank[J].IEEETransactiononSignalProcessingLetters, 2004, 11(2): 112-114.

[11]WUZH,NORDENEH.Astudyofthechar—acteristicsofwhitenoiseusingtheempiricalmodedecompositionmethod[J].ProceedingsoftheRoyalSocietyofLondonA, 2004, 460: 1 597-1 611.

(编辑：刘宝江)

Detecting voltage flicker signal based on Hilbert-Huang transform and EMD denoising

XU Xi-yu1,LI Zhen-mei1,LI Hai-tao1,MA Rui1,XING Dong-mei2

(1.School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255049,China (2.Wendeng Jinlida Steel Structure Company Limited , Weihai 264400, China)

Aiming at the increasing phenomenon of voltage flicker,a new method based on Hilbert-Huang Transform and EMD denoising is proposed for extracting feature information of voltage flicker.First, envelope signal could be extracted by using Hilbert-Huang Transform .Then the noises components of envelope signal could be removed by using EMD. Finally, the denoising envelope signal could be decomposed by using Empirical Mode Decomposition (EMD) for getting accurate amplitude modulation wave. Simulation results show that the accurate time, amplitude,frequency of signal which is non-stationary can be obtained through this new method. This method has good adaptability to different voltage flicker.

Hilbert-Huang Transform,EMD; flicker; amplitude modulation wave; envelope

2016-04-05

国家自然科学基金项目(51407112)

徐浠钰，男，xuxiyu486900@163.com; 通信作者：李震梅，女，lzm650208@126.com

1672-6197(2017)02-0008-05