中国城镇化的空间动力机制与效应——基于第六次人口普查2869个县域单元数据

赵果庆，吴雪萍

(云南财经大学 数量经济研究所，云南 昆明 650221)

中国城镇化的空间动力机制与效应
——基于第六次人口普查2869个县域单元数据

赵果庆，吴雪萍

(云南财经大学 数量经济研究所，云南 昆明 650221)

城镇化是一个空间现象。如何揭示与测度城镇化的空间动力机制，是经济地理学的一大难题。本文利用我国第六次人口普查的2869个区县域单元(县，区，市)城镇化率数据，通过构造空间动态计量模型揭示我国城镇化的空间动力机制。结果显示，以城市人口、人口迁入、工业化、地理位置为控制变量，我国城镇化具有稳健的二阶空间滞后动力机制。这表明，城镇化形成空间动力系统，一个县域单元的城镇化受周边两县域单元城镇化的促进。在城镇化空间动力效应作用下，我国已形成北部与东南部两个高城镇化区域，大西南区域的城镇化水平仍较低。因此，我国要加大力度促进“南方丝绸之路”城市群建设，重塑城镇化经济地理，促进城镇化的区域协调发展。

县域单元；城镇化；空间动力机制；空间计量；中国

一、问题提出

城镇化也称城市化(Urbanization)，是当今中国重要的社会、经济与空间现象之一，也是当今世界影响最大、最深刻、最全面的经济地理重塑。正如斯蒂格利茨所说：“中国的城市化与美国的高科技发展将是影响21世纪人类社会发展进程的两件大事。”他认为城市化将使中国成为世界领袖。究竟是什么动力推进着中国的城镇化？这是人口学、经济学、文化学、生态学、地理学等多学科理论探索与实证研究的焦点。

城镇化是一个复杂的、多层面的社会经济空间变迁的动态过程，是经济与非经济因素共同作用的结果。城镇化动力是城镇化研究中的核心问题。目前，学术界已对城镇化动力机制进行了大量的研究，总体上可分为定性与定量两条线路。

在定性方面，人口城镇化的根本动力在其初期主要来自工业化的进步，在中后期主要来自城市服务业的发展与新兴产业的创新[1]；后来出现了以多元城镇化动力替代以往一元或二元城镇化动力的新的机制形式[2-4]，人口迁移[5]、工业化[6]、乡镇企业[7]、外资[8]，文化[9]等均成为中国人口城镇化的重要动力因素。值得一提的是，宁越敏[10]从政府、企业、个人三个城市化主体的角度分析了90年代中国城市化的动力机制和特点。

在定量方面，学者们主要是对城镇化动力机制进行统计评价和实证研究。(1)城镇化动力机制的评价。纪晓岚和赵维良在中国城市化动力机制的分析框架下，构建了城市化动力机制评价指标体系，对城市化动力机制进行准确反映和综合评价，但没有具体评价出城市化动力机制[11-12]；曹广忠等[13]利用2000年截面数据，用因子分析法考察了东部沿海省区人口城镇化影响因素的差异、特征和类型；也有学者以四维分析视角对人口城镇化的动力过程进行了分析，总结出行政力、市场力、外向力与内源力等主要影响动力，并强调城镇化动力的多元化[14-15]。(2)实证研究。一些学者对部分地区如江苏[16]、广东[17]城市化动力机制的进行实证研究；陈波翀等[18]建立了不确定条件下农村剩余劳动力的城市化决策模型，认为城市化快速发展是政府和市场共同作用的结果；在对传统工业化与城市化之间数量关系进行计量分析的基础上，提出了城市化快速发展主要是由第三产业推动的观点。有的学者还应用VAR模型分别对内蒙古和新疆城镇化的时间动力机制进行了实证研究[19-20]。

近年来，随着地理信息技术的快速发展，越来越多的学者开始将空间计量分析等方法运用到人口城镇化动力机制的研究中[21-23]。从方法上，除非传统的空间计量模型外，庞瑞秋等[24]还使用了地理加权回归模型(GWR)，邓志旺[25]最先依据空间杜宾模型构建中国城市化动力机制模型，并分别进行时间固定效应模型、空间固定效应模型以及双固定效应模型回归检验本地区城市化水平的提高将会对其他地区城市化的发展所具有促进或阻碍作用。

不难看出，揭示城镇化动力机制是一个重要的研究领域，目前已取得了丰硕成果，但探索城镇化动力机制的研究远没有结束。城镇化也是一个空间现象。虽然，国内学者应用空间计量实证了城镇化动力机制的存在，但是仅把空间作为一个动力因素来看待，并没有揭示出具体的空间动力机制。城镇化是人口迁移引起人口经济重塑的必然结果。空间力量是城市化的重要力量[26]，空间动力机制也同样是城市化不可缺失的重要机制。观察发现，在我国城镇化水平高的地区如长三角地区和珠三角地区会成片出现，而城镇化水平较低的地区也相对成片出现，城镇化呈现出空间集聚的特征。为什么会有这种现象？我们猜想，这是空间单元城镇化相互作用的结果，进一步体现为空间动力机制产生的效应。类比时间动力机制，空间动力机制也应是一种空间滞后自相关现象。也就是说，空间动力机制来源于空间单元相互依赖产生系统性。而区域相互依赖的原理规律及测算方法仍是一道尚未得到解决的地理学难题[27]。这说明，揭示城镇化的空间动力机制是地理学的一大难题。目前，基于空间计量研究了空间单元的空间相邻自相关，所揭示的是城镇化空间集聚机制，因此，有必要从空间滞后自相关的角度予以审视城镇化的空间动力机制。这不仅是对城镇化动力机制研究的有效完善，而且更是对中国城镇化空间过程演化机理的深入探索。

本文沿第二条线路，从空间滞后自相关视角探寻城镇化的空间动力机制。本文创新之处主要在于用空间单元的城镇化滞后自相关中发现我国城镇化的空间动力机制，并以人口迁入率、工业化水平和地理位置为控制变量对其进行对稳健性检验；其次，本文在2869个县区市(县、区、市，下同统称县域)空间单元第六次人口普查的大样本数据中通过可视化展示出我国城镇化空间动力效应的空间结构，有助于认清我国城镇化发展的空间力量格局，为重塑城镇化经济地理、优化城镇化空间布局提供政策依据和支持。

二、研究方法与模型构建

(一)城镇化的空间效应

人类活动是在一定的空间范围内进行的，也就是人们的经济社会活动要受空间因素的制约。人类行为与所在地区有着密切关系，依据引力定律，此种关系随著距离的增大而递减。具体地，空间有两个重要的效应，一是集聚效应，二是位置效应。“物以类聚，人以群居”是一个自然的现象。集聚成为人类空间经济活动的一种属性，其表现为对空间的依赖性，本地依距离受相邻地区的影响。按新经济地理学解释，人口集聚或聚类产生可以节约资源和交易成本，具有外部性，规模效应和溢出效应。在现实人口分布中，具有高人口密度地区会在空间“抱团”集聚在一起，产生城市与城市群，进而出现高水平的城镇化集聚区或城镇化带。

从空间位置看，纬度决定气候，气候又影响生产环境和人的生产力，进一步影响城镇化。由于地理位置决定着交通的通达程度、离出海口的距离，决定着运输成本。同时地理位置决定着宜居性，空间异质性产生不同的人口集聚区。城市化有着向低纬度地区发展，是一个规律。从我国看，东南沿海低海拔地区拥有众多的港口码头和低成本的航运优势，国际贸易较为发达，形成人口的集聚生产力，具有其它地区无法比拟的地缘优势，而西北地区不具有人口集聚的有利地理条件和区位优势，地广人稀，人口的集聚功能较弱。从世界上看，大多数大城市分布在气温适中的中纬度地带，其中又明显集中于年降雨量在400mm以上的湿润半湿润地区，而气候恶劣的荒漠干旱地区，高纬度寒冷地区，海拔3500米以上的高原和湿热的热带雨林地区则鲜有人居住。地理因素通过对经济发展的促进或限制而影响到城镇化的发展[28]。

城市是人口在一定地域范围的大量集聚和有效集中的空间形态，而人口城镇化在一定程度上体现着人口集聚，城镇化成为当代人口生存与发展最有效的空间组织机制。我国区域经济无论在单个城市、城市群的层面上，还是在经济地带的层面上，城镇化都表现出明显的集聚趋势。相对来说，在人口城镇化进程中，资源、地理位置、气候等地理因素(或者说传统的经济地理因素)对人口城镇化发展的过程中的确起着根本性的作用，而其中特别重要的则是空间集聚动力与地理位置。实证表明，区位地理条件是城市规模等级序列的首要要素[29]。显然，理解空间的动力机制直接关系到城镇化发展战略。

在空间效应下，我国人口分布具有极大的差异，形成了东部—中部—西部的东高西低梯度集聚的格局。最为突出的是“胡焕庸线”所说明的区域分异现象。不论是历史因素，还是改革开放以来的新因素，“胡焕庸线”*胡焕庸线(Hu Line，或Heihe-Tengchong Line，或Aihui-Tengchong Line)，即中国地理学家胡焕庸(1901-1998)在1935年提出的自黑龙江瑷珲至云南腾冲画出一条我国人口密度对比线(约为45°)，线东南半壁36%的土地供养了全国96%的人口；西北半壁64%的土地仅供养4%的人口，二者平均人口密度比为42.6∶1。“胡焕庸线”不仅是人口界线，同时为一条中国生态环境界线和适宜人类生存地区的界线。所揭示的人口分布规律依然没有被打破。

(二)城镇化的空间滞后自相关

空间集聚是空间自相关的具体表现。城镇化的空间动力机制来自空间滞后自相关性。如果，城镇化存在空间动力机制，那么各空间单元之间的城镇化之间存在空间自相关性。这种空间自相关与时间序列自相关类似，表现为空间依赖性中的空间滞后效应。只要城镇化存在显著的空间自相关，就可将其分成四类集群，在空间上形成中心—外围结构。具体到中国的具体国情，县域相邻空间单元与其滞后空间单元的城镇化在地理空间上表现出一定的相关性，就说明县域城镇化的空间相互作用或影响的途径可以通过邻接县域而相互传递。检验县域城镇化的空间相关性存在与否，在实际的空间相关分析中可以使用空间自相关指数Moran’I，但是空间滞后自相关指数与Moran’I仍有一定差别。为直接分析空间滞后自相性，这里采用空间自关系数[30]。空间滞后自相关系数定义如下：

(1)

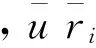
(三)地理位置相关与趋势面

地理位置相关性是研究一个观察变量与一个地理变量的关系是否密切。地理相关系数就是用来研究空间变量与地理位置要素间的相互关联强度的一种度量指标。城镇化率的地理相关系数计算公式：

(2)

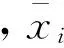
城镇化与地理位相关性分析揭示了城镇化与地理位置之间的相关程度，但是当使用经度和纬度进行相关分析时，只能反映东西或南北关系。如果要分别做回归分析，那么就会产生两个回归模型，尚不能确定城镇化与空间位置的关系。因此，客观需要经度和纬度同时进入一个回归模型，一般情况还是非线性方程，这就产生了趋势面分析。趋势面分析就是用空间数据拟合一个数学曲面，以反映观察变量空间分布的变化趋势特征。实际上，趋势面分析是通过回归分析原理，运用最小二乘法拟合一个二维函数，应用线、面或三维曲面来识别、分离和度量趋势的一种空间分析方法[31]。

趋势面反映的是总体变化，受大范围的系统性空间位置的影响。趋势面分析的基本功能，是把空间分布的一个具体的或抽象的曲面分解成两部分：一部分主要由变化比较缓慢、影响遍及整个研究区域分量组成，称为趋势分量；另一部分是变化比较快，其影响在研究区域内并非处处可见的分量，称为局部分量。设(xi,yi)表示某一观察变量Yi对应于空间位置，xi、yi分别为经度和纬度值。每一个观测点的Yi都可分解为两个部分：

Yi=f(xi,yi)+εi

(3)

(3)式中，f(xi,yi)为Yi的趋势量，εi为残差值。趋势面模型的数学方程式为多项式函数：

f(xi,yi)=a00+a10xi+a01yi

(4)

(5)

(6)

(4)式为一次多项式，是一个平面。它可以是水平的，但极少见，一般是以某倾角倾向于某一方向。(5)式为二次多项式曲面，可以是椭圆面，双曲面，或是抛物面，只有一个极值点的曲面。(6)式三次多项式曲面，可以出现四个极值点，多为马鞍型三次曲面。但在建立实际模型时，有些项不显著，一般只使用多项式函数中的几项。不同次数的多项式函数所描述的曲面有不同的复杂程度。

(四)城镇化空间动力机制计量模型

在采用传统的计量分析方法时，隐含假设横截面空间单元是同质的，也就是空间单元之间没有自相关性或集聚。而实际上，根据“地理学第一定律”，几乎所有的空间数据都具有一定程度的空间依赖性或空间自相关性的特征。经济的动力机制就来源于空间单元的经济空间依赖性[32]。具体到城镇化，亦即一个空间单元上的城镇化水平与邻近空间单元上的城镇化水平是正相关的，这种自相关性是城镇化空间动力机制的来源。

空间计量经济学的基本思想是将空间单元之间的空间依赖关系引入基本线性回归模型[33-34]。借鉴时间动力机制的AR模型，引入空间滞后变量，建立在控制变量作用下的城镇化空间动力机制模型即SAR(q)模型：

(7)

(7)式为在考虑其它因素影响下，多阶空间空间滞后自相关模型，其中，ur为城镇化率，X为控制变量，wi-k, j-k为n×n阶的空间滞后相邻矩阵，i=1，2，…，n；k滞后阶数，λk是空间动力效应系数。

城镇化空间相关分为空间自相关与空间位置相关。因此，只有把空间自相关与空间位置相关结合起来，才能更有效地解释空间因素对城镇化的影响。另外，城镇化与城镇人口有关，城镇人口规模越大，城镇化水平越高；城镇化还与人口迁移和工业化存在正向关系[5-6]。基于上此，构造出我国城镇化空间动力机制的空间杜宾计量模型：

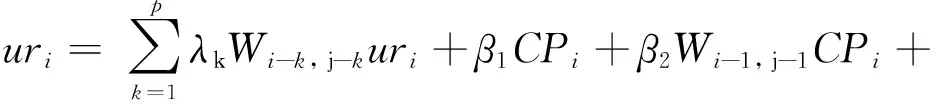
β3IPi+β4Wi-1, j-1IPi+β5Ii+β6Wi-1, j-1Ii+

f(xi,yi)+εi

(8)

(8)式中CPi、IPi、Ii和f(xi,yi)为控制变量，用于检验假设及空间动力机制的稳健性。其中，CPi表示城镇人口总量，IPi为迁入人口量，Ii表示工业化率，f(xi,yi)为地理位置效应。

(9)式揭示了县域城镇化率的拟合值，而偏差表示县域城镇化实际值和拟合值之差，即：

(9)

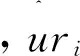
三、数据来源

(一)数据来源

本文数据来自《中国2010年人口普查分县资料》[33]提供的第六次人口普查分2869个县域相关数据计算，其中，城镇化率为城镇人口/总人口，人口迁入率为迁入人口/总人口，工业化率以第二产业人口占全行业人口比重表示。此外，代表县域地理位置的经度和纬度数据来自国家地理信息系统网站。

(二)数据描述性统计

从表1可以看出，各个变量的差别非常大，选择的2869个县域中有的城镇化率达到100%，也有城镇化率仅为1.38%的县域，工业化率、人口迁入率和城镇化人口规模分布均呈非正态分布，存在着两极分化的现象，最大值和最小值相差较大。

表1 2010年我国县域人口城镇化率、工业化率、人口迁入率的描述性统计

(三)城镇化率空间分布

城镇化率是城镇化发展水平的关键指标，其空间分布基本可以代表城镇化发展水平分布。以2010年我国城镇化率平均值(46.91%)为界线，超过平均水平的县域有1065个，其平均城镇化率为75.23%；低于平均水平的县域有1804个，其平均城镇化率仅为30.19%。城镇化率超过平均值的县域分布相对集中，包括两个主集聚区和两个次集聚区。其中主集聚区：一是在东经120度，北纬30度附近，以上海为中心主要包括浙江、江苏的长三角地区；二是在东经115～125度，北纬35～42度的环渤海经济地区，包括山东，河北、北京和天津。两个次集聚区分别是广东珠三角和福建(图1)。可见，高发展水平县域主要分布在东部沿海一带地区，大部分中部和西南地区很少有高发展水平县域分布。而城镇化率小于平均水平的地区，全国31个省市都有分布，主要集中在东经97～115度，北纬23～40度区域，以西南地区和广大中部地区为主，东南沿海县域分布很少，已是点缀其中(图2)。

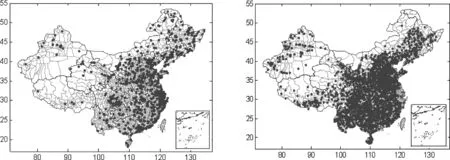
图1 2010年城镇化率高于平均值的县域分布 图2 2010年城镇化率低于平均值的县域分布

按(2)式计算，我国县域城镇化率与经度的相关系数为0.1835，与纬度的相关系数为0.1718。当N为1000时，0.1%显著性水平为临界值为0.104。可见，两者均在0.1%的水平上显著。这表明，县域城镇化率随东经和北纬的增加而增大，以随东经的增加更为明显。也就是说，东南部城镇化率明显高于西北部。总体上，我国城镇化率分布与地理位值具有极强的相关性，我国南北差距相对较小，而东西差距更大。

四、城镇化滞后自相关检验与空间动力机制参数估计

(一)城镇化空间自相关与显著性检验

根据我国2869个县域的经度和纬度计算，得到我国县域1-3阶和4-6阶滞后的空间矩阵结构(图3和图4)。以(1)式计算，2010年城镇化率的滞后1-6阶空间自相关系数分别为0.5457、

0.5408、0.4772、0.4014、0.3726和0.3392，均为正值，且在1%的水平上显著，显示出了很强的空间滞后自相关性。可以看出，我国县域城镇化水平的空间自相关系数随滞后期数的增加而递减。这也意味着，我国城镇化的空间动力随空间距离增大而减小。相对而言，一阶滞后的城镇化率空间自相关系数最大，表明对一个县域来说，最邻近的县域城镇化率对其城镇化水平的作用越明显。

(二)城镇化空间动力模型参数估计

由于县域之间的人口城镇化水平存在显著的空间滞后自相关性，所以必须采用控制了空间自相关性的空间计量模型对各动力因素的贡献进行分析，以得到回归系数的无偏估计量。利用2010年的2869个县域数据对(8)式进行回归分析，得到参数估计结果(表2)。

图3 1-3阶空间滞后矩阵 图4 4-6阶空间滞后矩阵

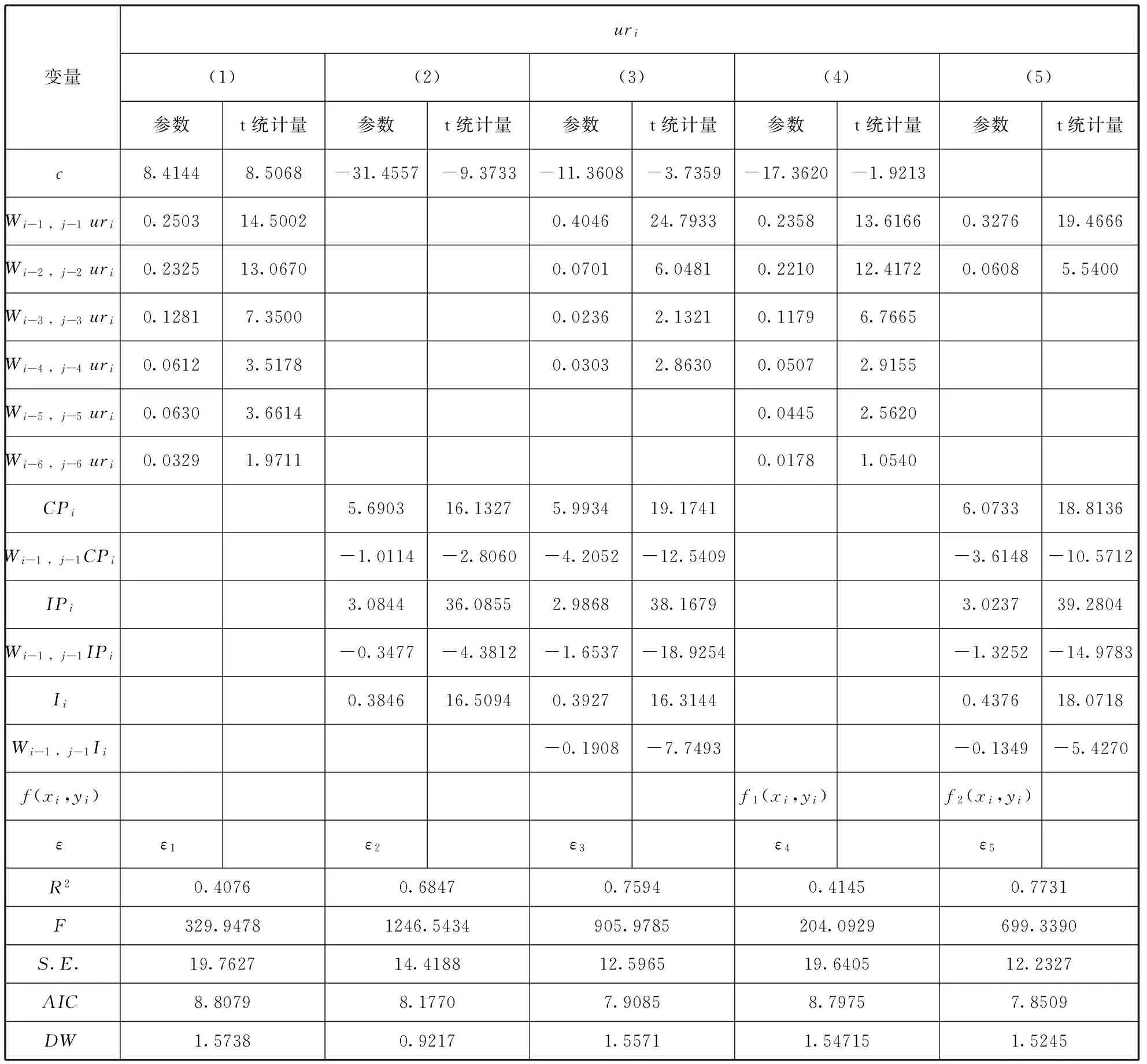
变量uri(1)(2)(3)(4)(5)参数t统计量参数t统计量参数t统计量参数t统计量参数t统计量c8.41448.5068-31.4557-9.3733-11.3608-3.7359-17.3620-1.9213Wi-1,j-1uri0.250314.50020.404624.79330.235813.61660.327619.4666Wi-2,j-2uri0.232513.06700.07016.04810.221012.41720.06085.5400Wi-3,j-3uri0.12817.35000.02362.13210.11796.7665Wi-4,j-4uri0.06123.51780.03032.86300.05072.9155Wi-5,j-5uri0.06303.66140.04452.5620Wi-6,j-6uri0.03291.97110.01781.0540CPi5.690316.13275.993419.17416.073318.8136Wi-1,j-1CPi-1.0114-2.8060-4.2052-12.5409-3.6148-10.5712IPi3.084436.08552.986838.16793.023739.2804Wi-1,j-1IPi-0.3477-4.3812-1.6537-18.9254-1.3252-14.9783Ii0.384616.50940.392716.31440.437618.0718Wi-1,j-1Ii-0.1908-7.7493-0.1349-5.4270f(xi,yi)f1(xi,yi)f2(xi,yi)εε1ε2ε3ε4ε5R20.40760.68470.75940.41450.7731F329.94781246.5434905.9785204.0929699.3390S.E.19.762714.418812.596519.640512.2327AIC8.80798.17707.90858.79757.8509DW1.57380.92171.55711.547151.5245

(2.0156) (4.1613) (-3.3863) (2.6832)

(-3.1608) (3.9335) (3.3601) (-4.3957)

(-3.7095) (4.8521)

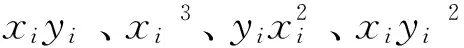
值得一提的是，DW在时间序列计量经济学中用于检验残差项的序列自相关。在时间序列中时间序列是单向的，且是唯一的，而从空间看，空间位置是固定的，由距离决定，空间滞后也是唯一的。因此，以可以借用DW检验一种特定排列的空间计量模型残差序列的自相关性。从表2看，(2)中没有城镇化的的空间滞后变量，仅有控制变量及其一阶空间滞后变量，DW值仅为0.9217，ε2存在较强的空间自相关性，而(1)、(3)、(4)和(5)中具有多项城镇化的空间滞后变量，其DW值在1.5以上，残差序列中的的自相关性已较弱。显然，城镇化空间滞后变量已消除了空间自相关。

(三)城镇化空间动力机制化的稳健性检验

从表2的(1)看出，在不考虑其它因素的情况下，在5%的显著性水平上，中国城镇化具有显著的5阶滞后空间动力机制。从1阶到5阶，t值大幅度减小，空间动力的边际效应也大幅度减小。(5)表明，城市人口规模、人口迁入量、工业化水平与空间位置对城镇化的空间动力机制产生明显的影响，对3阶到5阶空间动力因子产生了挤出效应。这也就是，在控制变量作用下，我国城镇化只具有稳健的空间二阶滞后动力机制。

五、可视化分析

(一)LISA集群与可视化

表2中(5)表明，我国城镇化具有稳健的一阶、二阶空间滞后动力机制。这表明，县域城镇化具有较强的一阶、二阶滞后自相关性，城镇化率与其滞后一阶和二阶滞后城镇化率平均值的相关性为0.6138，在大样本下表现出极强的显著性。以城镇化率与其滞后一阶和二阶城镇化率的平均值(46.9149，50.8711)为坐标原点，把我国县域分为四类集群：HH集群，由一个高城镇化率县域与其滞后一阶和二阶平均高城镇化率县域构成；LH集群，由一个低城镇化率县域与其滞后一阶和二阶平均高城镇化率县域构成；LL集群，由一个低城镇化率县域与其滞后一阶和二阶平均低城镇化率县域构成；HL集群，由一个高城镇化率县域与其滞后一阶和二阶平均低城镇化率县域构成。

图5是以一阶和二阶滞后城镇化率平均值计算的我国县域城镇化四分类结构。其中，HH类、LH类、LL类和HL类的数量分别为754、446、1358和311，占总县域数的26.28%、15.55%、47.33%和10.84%。不难看出，我国LL类的样本占比较大比重，接近50%，其次是HH类，两类并在一起占72%，它们是我国城镇化空间滞后自相关的主导力量，呈现出典型的空间俱乐部特征。

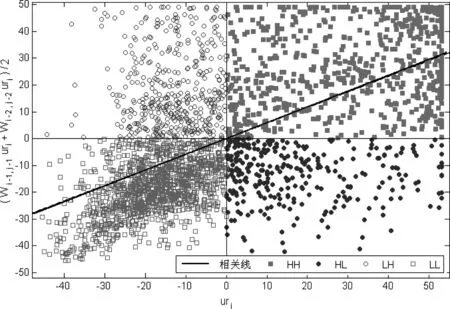
图5 城镇化率与其1、2阶滞后空间变量平均值相关性

把图5中的四象限的县域在空间展开，分别得到图6-9。HH类县域主要分布在黑龙江省东部与俄罗斯接壤的地区，辽宁省的沈阳等几个主要城市；外向型经济特征明显的长三角地区到珠三角地区形成的东南沿海地带；西部乌鲁木齐与克拉玛依、内蒙中南部与东北部区域也比较集中，其它地域和零星分布，西藏没有分布(图6)。LL类县域主要分布在次沿海与次沿边的腹地较大区域，沿边分布较少，沿海的长三角和珠三角地区有较少分布出现(图7)。HL类和LH类县域主要分布在我国东南部，西藏、内蒙、新疆、甘肃、宁夏分布较少，西藏没有LH类县域分布(图8和图9)。

(二)城镇化空间动力机制与效应趋势面

表2中的(5)表明，我国城镇化具有稳健的一阶、二阶空间滞后的动力机制，因此，再对一阶、二阶空间滞后的联合动力机制进行估计，SAR(2)模型：

uri=0.4396Wi, i-1uri+0.4307Wi, i-2uri+εi

(10)

(28.0986) (27.0167)

R2=0.3202，DW=1.7672，AIC=8.9437。

对比(10)式与表2中的(1)，(10)式的R2值小于(1)的R2值，而(10)式的AIC值高于(1)的AIC值，但(10)没有截距项，其DW值高于(1)的DW值。这说明(10)代表着主要的空间动力机制。图10为(10)式拟合城镇化率的空间动力效应的趋势面。

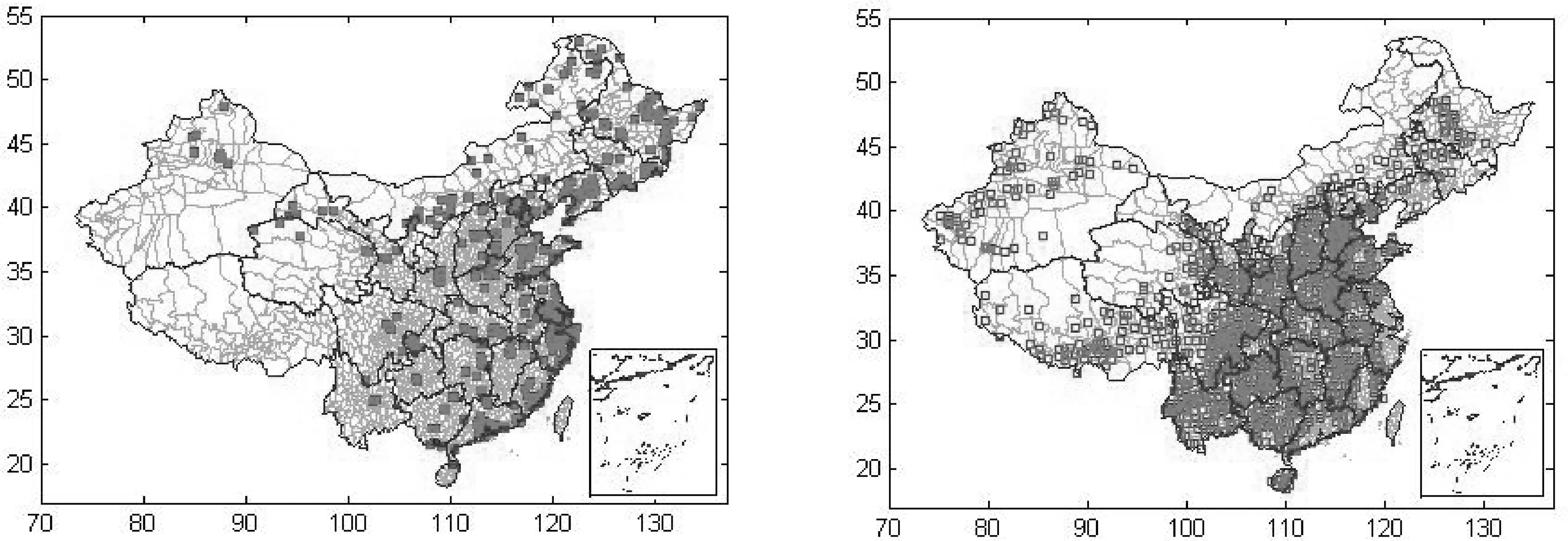
图6 2010年我国HH类县域分布 图7 2010年我国LL类县域分布

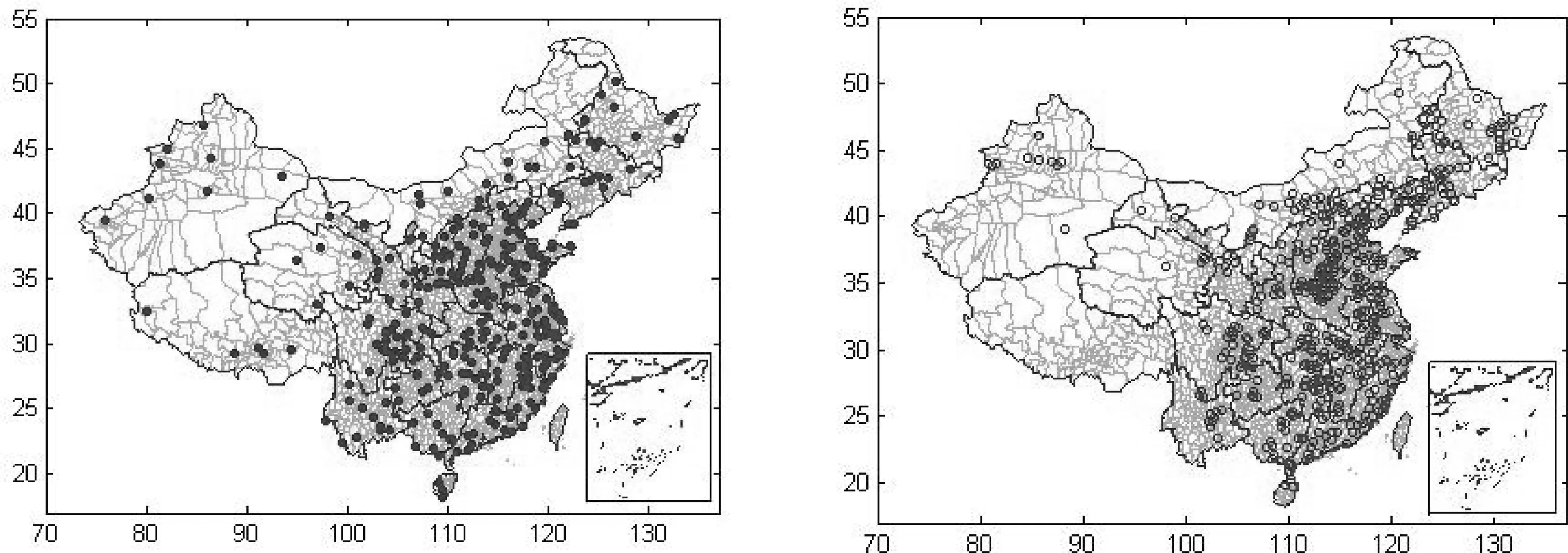
图8 2010年我国HL类县域分布 图9 2010年我国LH类县域分布

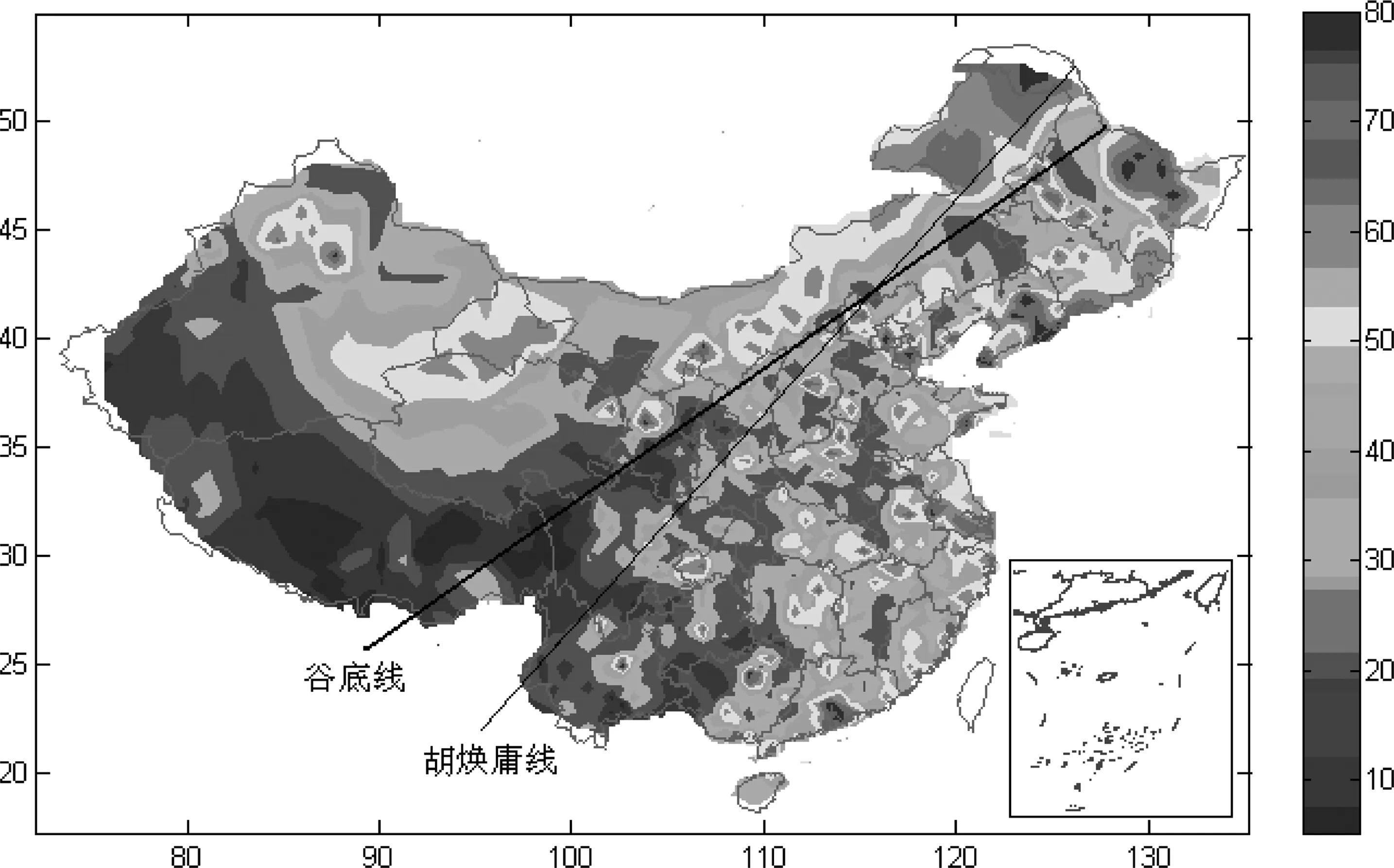
图10 我国城镇化SAR(2)动力效应的空间分布

图10显示，中国的版图上，城镇化空间动力效应分布空间趋势面具有多中心—外围结构，而总体形态呈鞍型结构，可以划分为四个区域。(1)由东南沿海、环勃海和东北三省东部沿边地带构成一个高城镇化区域。(2)由北部沿边地带主要是新疆东北部、青海北部、甘肃西北部、宁夏北部、陕西北部、内蒙沿边区域、内蒙与黑龙江交界地区构成的高城镇化区域。(3)由新疆西南部、西藏、青海南部、宁夏南部、甘肃南部、四川西北部、云南西北部连片形成低城镇化大区域(简称“大西南片区”)。(4)由内蒙古自东南部、黑龙江中部、吉林北部构成了另一个低城镇化小区域。此外，在安徽、河南、江苏、山东和河北的交界处有一个低城镇化小区域，江西等也有低城镇化区的零星分布。除西藏外，每一个省份都有超过50%的高城镇化局部小区域分布。很明显，我国城镇化水平具有明显的多元化差距特征，空间异质性较为突出。

不难发现，两个高城镇化区域分布在“胡焕庸线”的两侧(图10)。从空间动力效应看，城镇化低谷区域也形成了从西藏错那县勒门马巴民族乡到黑龙江萝北名山镇的一条分界线，称城镇化空间动力效应“谷底线”。按两地东经和北纬计算，“谷底线”长达4899.50公里。“谷底线”与“胡焕庸线”交于河北张家口市沽源县九连城镇。

(三)残差空间趋势面

(10)式的εi值序列只有较弱的空间自相关性。从图11看出，非空间动力效应在全国范围只有局部的特征，没有趋势和规律所循，但也有一些明显的特点。非空间动力强正效应(>20)的区域分布在北部，尤其是在青海、新疆和甘肃交界区域具有较强的城镇化非空间动力效应，在内蒙古东北部也有非空间动力效应优势。非空间强阻力效应(<-40)区域呈分散分布，在西部的云南、四川、重庆分布较少，在广东、福建、江苏、浙江、山东为主的东南沿海区域更是少见。

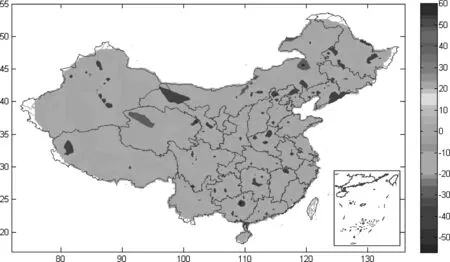
图11 我国城镇化的非空间动力因素效应(εi)的空间分布

六、结论与含义

本文利用我国第六次人口普查的2869个区县域单元城镇化率数据，通过构造动态空间计量模型，揭示我国城镇化的空间动力机制与效应。结果表明：

一是城镇化空间扩展的过程和格局受空间动力机制的影响。在城市人口规模、人口迁入量、工业化水平及地理位置参与的情况下，我国城镇化仍具有稳健的空间二阶滞后动力机制。中国每个县域空间单元的城镇化水平对其最近两个县域空间单元的城镇化存在明显的空间依赖性。这意味着孤立县域空间单元的城镇化难以推进，县域空间单元越密集，城镇化越易抱团发展。这就是我国版图上形成高城镇化水平集聚区和低城镇化水平集聚区的根本原因。

二是城镇化是一个复杂的、多层面的社会经济空间变迁的动态过程，是多动力综合作用结果。我国城市人口规模、人口迁入量、工业化水平及其地理位置也是城镇化的显著动力因素。这意味着，我国在制定区域政策时，既不能以地理决定论的观点夸大地理因素作用而忽视政府的宏观调控作用，也不能以非地理因素排斥或忽视空间效应，以导致在调节城镇化发展差距政策效应受到空间力量阻制与抗拒，过高预期政策对城镇化不发达区域的促进作用。

三是在空间动力机制影响下我国城镇化空间分布呈现出鞍型结构。在我国北部沿边已突破了“胡焕庸线”，形成多个高水平城镇化集聚区，这意味着，我国人口分布难以突破“胡焕庸线”，但城镇化可以突破“胡焕庸线”，这一点对中国具有特殊的意义。目前，“胡焕庸线”西南端“次大西南片区”的城镇化仍然相对滞后，主要是城镇化的空间动力不足。我国要加大对“大西南片区”发展的政策支持力度，加快人口迁移，扩大城市人口规模，提升人口密度，提高城镇化率，重塑经济地理，同时，要进一步推进“三纵两横”的城镇化战略，加快南方丝绸之路经济带工业化发展，让“大西南片区”居民分享城镇化和工业化的成果。

[1] 赵新平，周一星. 改革以来中国城市化道路及城市化理论研究述评[J]. 中国社会科学，2002(2)：132-138．

[2] 宁越敏. 新城市化进程: 90年代中国城市化动力机制和特点探讨[J]. 地理学报, 1998, 53(5): 470-477.

[3] 周一星, 曹广忠. 改革开放20年来的中国城市化进程[J]. 城市规划，1999, 23(12): 8-13.

[4]蔡建明. 中国城市化发展动力及发展战略研究[J]. 地理科学进展, 1997, 16(2) :9-14.

[5]ZhangKH,SongS.Rural-urbanmigrationandurbanizationinChina:Evidencefromtime-seriesandcross-sectionanalyses[J].ChinaEconomicReview, 2003, 14(4):386-400.

[6]顾朝林. 改革开放以来中国城市化与经济社会发展关系研究[J]. 人文地理, 2004, 19(2): 1-5.

[7]崔功豪, 马润潮. 中国自下而上城市化的发展及其机制[J]. 地理学报, 1999，54(2): 106-115.

[8]薛凤旋, 杨 春. 外资: 发展中国家城市化的新动力——珠江三角洲个案研究[J]. 地理学报, 1997, 52(3): 193-206.

[9] 俞万源. 城市化动力机制: 一个基于文化动力的研究[J]. 地理科学, 2012, 32(11): 1135-1139.

[10] 宁越敏. 新城市化进程: 90年代中国城市化动力机制和特点探讨[J]. 地理学报, 1998, 53(5): 470-477.

[11] 纪晓岚, 赵维良. 中国城市化动力机制评价指标体系的构建[J]. 统计与决策, 2007, 233(3): 70-72.

[12] 赵维良, 纪晓岚. 中国城市化动力机制评价指标体系的构建[J]. 上海市经济管理干部学院学报, 2007, 5(6): 52-58.

[13] 曹广忠, 王纯洁, 齐元静. 我国东部沿海省区城镇化水平影响因素的空间差异[J]. 地理研究, 2008, 27 (6):1399-1406.

[14]欧向军, 甄峰, 秦永东等. 区域城市化水平综合测度及其理想动力分析: 以江苏省为例[J]. 地理研究, 2008, 27(5): 993-1002.

[15]陈明星, 陆大道, 张华. 中国城市化水平的综合测度及其动力因子分析[J]. 地理学报, 2009, 64(4): 387-398.

[16] 吴莉娅. 生产要素市场化与江苏城市化动力机制演变[J]. 地理科学, 2006, 26(5): 529-535.

[17] 陈德宁, 沈玉芳. 广东城市化的动力特征与发展方向探讨[J]. 经济地理, 2004, 24(1): 76-80.

[18] 陈波翀, 郝寿义, 杨兴宪. 中国城市化快速发展的动力机制[J]. 地理学报, 2004, 59(6):1068-1075.

[19] 王瑞鹏, 冯晓华. 基于VAR模型的新疆城市化动力机制研究[J]. 企业经济, 2013,(2): 149-153.

[20] 耿丽娟. 基于VAR模型的内蒙古城镇化动力机制研究[J]. 内蒙古科技与经济, 2015, 333(11): 21-23.

[21] 柳思维, 徐志耀, 唐红涛. 基于空间计量方法的城镇化动力实证研究——以环洞庭湖区域为例[J]. 财经理论与实践, 2012, (4):100-104.

[22] 曾昭法, 左 杰. 中国省域城镇化的空间集聚与驱动机制研究——基于空间面板数据模型[J]. 中国管理科学, 2013, (S2): 580-586.

[23] 王小斌, 邵燕斐. 基于空间计量的新型城镇化动力机制研究[J]. 工业技术经济,2015(12): 144-155.

[24] 庞瑞秋, 腾 飞, 魏冶. 基于地理加权回归的吉林省人口城镇化动力机制分析[J]. 地理科学, 2014, 34(10): 1210-1217.

[25] 邓志旺. 中国城市化动力机制的模型构建及其空间计量分析[J]. 统计与决策, 2015, 427(25):129-131.

[26] 陆 铭. 空间的力量: 地理、政治与城市发展[M]. 上海：格致出版社, 2012.

[27] “10000个科学难题”地球科学编委会. 10000个科学难题(地球科学卷)[M]. 北京：科学出版社, 2010.

[28] 陆大道．地理学关于城镇化领域的研究内容框架[J].地理科学，2013，33(8):897-901．

[29]PeterChristensen,GordonC.McCord．GeographicdeterminantsofChina’surbanization[J].RegionalScienceandUrbanEconomics, 2016, (59): 90-102.

[30] 罗宏翔, 赵果庆.FDI产业空间自相关与空间集聚——再论为什么FDI不集聚西部[J]. 经济管理, 2012, (9): 37-45.

[31] 郭仁忠. 空间分析[J]. 北京：高等教育出版社, 2001.

[32]RobertoBasile,MaríaDurbán,RománMínguez,JoseMaríaMontero,JesúsMur.Modelingregionaleconomicdynamics:Spatialdependence,spatialheterogeneityandnonlinearities[J].JournalofEconomicDynamicsandControl, 2014, 48: 229-245.

[33]L.Anselin.Spatialeconometrics:methodsandmodels[M].Dordrecht:KluwerAcademicPublishers, 1988.

[34]AnselinL,FloraxR.Smallsamplepropertiesoftestsforspatialdependenceinregressionmodels[C].InAnselinandFloraxREds.NewDirectionsinSpatialEconometrics.Berlin:Springer, 1995, 21-74.

(本文责编：王延芳)

Spatial Dynamic Mechanism and Effect of Urbanization in China Based on Spatial Unit Data of 2869 Counties Derived from the Sixth Census

ZHAO Guo-qing，WU Xue-ping

(InstituteofQuantitativeEconomics，YunnanUniversityofFinanceandEconomics，Kunming650221，China)

Abstract:Urbanization is a phenomenon of space, how to reveal the space dynamic mechanism of urbanization is a major difficult problem of geography. In this paper, using the 2869 county urbanization rate data of our sixth census, by constructing dynamic spatial econometric model reveals the space dynamic mechanism of urbanization in China. The results show that to urban population, population migration, industrialization, geographical location as a control variable, urbanization in china still has a robust spatial second-order lag dynamic mechanism and urbanization formation a spatial dynamic system, it is shown that a county urbanization is promoted by two surrounding counties. Under the effect of the dynamic effect of urbanization, the high level of urbanization in the north and the south has formed and big Southwest regional urbanization level is still relatively low. Therefore, China should intensify efforts to promote the construction of the“Southern Silk Road” urban agglomeration, reshape the economic geography of the city, and promote coordinated development of regional urbanization.

county unit; urbanization; spatial dynamic mechanism; spatial econometrics; China

2016-11-10

2017-02-08

国家自然科学基金项目(71563059)。

赵果庆(1964-)，男，云南鹤庆人，云南财经大学教授，经济学博士，博士后，博士生导师，研究方向：数量经济。

C813

A

1002-9753(2017)02-0076-12