30 t轴重重载铁路简支梁桥-轨道系统地震响应研究

闫 斌, 潘文彬, 刘 施, 戴公连, 魏 标

(1. 中南大学 土木工程学院，长沙 410075; 2.高速铁路建造技术国家工程实验室，长沙 410075)

30 t轴重重载铁路简支梁桥-轨道系统地震响应研究

闫 斌1,2, 潘文彬1, 刘 施1, 戴公连1,2, 魏 标1,2

(1. 中南大学 土木工程学院，长沙 410075; 2.高速铁路建造技术国家工程实验室，长沙 410075)

为研究多跨30 t轴重重载铁路简支梁桥-轨道系统地震响应规律，采用经过验证的梁轨相互作用模拟方法，建立了考虑桩-土共同作用、桥墩弹塑性变形、滑动支座摩阻力、线路非线性阻力的多跨重载铁路简支梁桥与双线有砟轨道相互作用仿真模型，揭示了一致激励和行波效应下重载铁路简支梁桥-轨道系统地震响应规律，探讨了路基段钢轨长度、简支梁跨数、跨度、线路纵向阻力形式、滑动支座摩阻系数等设计参数的影响，分析了温度、列车制动和地震耦合作用下系统的受力特征。研究表明：当地形地质条件相差不大时，简支梁跨数可简化为11跨、路基段钢轨长度可取为150 m；线路阻力减小时，梁体间、梁体与桥台间可能出现碰撞现象甚至发生落梁；纵向一致激励下，钢轨应力包络图呈“双菱形”，其最大值出现在桥台附近，而梁缝附近梁轨相对位移较大，易发生动力失稳；行波效应下，系统受力和变形规律发生显著改变，即使对于跨度较小的简支梁桥，也应考虑行波效应的影响；温度和列车制动作用将进一步增大轨道结构在地震中发生动力失稳的可能性。

重载铁路；铁路桥梁；简支梁；无缝线路；地震响应

为提高铁路运输能力、满足日益增长的铁路运输需求，重载铁路成为我国铁路建设的发展重点，而提高轴重是进一步提高货运量、降低运行成本的有效措施[1]。目前，我国正在规划和建设(改建)运行轴重30 t列车的重载铁路，如山西晋煤-渤海湾铁路、朔黄铁路、山西中南部铁路通道和蒙西至华中运煤通道等[2]。与以往的铁路桥梁不同，重载铁路桥梁除结构形式特殊外，还有轴重大、运量高的特点，且桥上采用75 kg/m焊接长钢轨。近年来，我国地震频发，在西部地区修建重载铁路时还将面临地震的严峻考验，桥梁及轨道结构一旦在地震中受到破坏，将造成难以估量的经济损失。

目前，国内外学者已对重载铁路标准活载模式[3-4]、既有桥梁对重载列车适应性[5]、重载铁路桥梁动力疲劳特性[6]，以及重载铁路桥上无缝线路纵向力分布规律[7]等课题进行了较为深入的研究，但地震作用下重载铁路桥梁与轨道系统的动力响应特征仍不明确。

本文针对30 t轴重重载铁路标准跨度简支梁桥，基于大质量法建立可考虑非一致激励的多跨32 m重载铁路简支梁桥-轨道系统动力仿真模型，研究一致激励及行波效应作用下桥梁-轨道系统受力和变形特征，并探讨关键设计参数对系统地震响应的影响规律。

1 重载铁路桥梁-轨道系统地震响应仿真模型

1.1 仿真模型的建立

假设轨道和梁体间不发生横向相对位移，采用带刚臂的梁单元模拟梁体。简化起见，用道床阻力代替线路纵向阻力[8]，并采用非线性杆单元模拟，其滞回曲线[9]如式(1)所示。

(1)

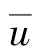
采用梁单元模拟钢轨，在桥台两侧各建立150 m路基上的钢轨[10]，采用线性弹簧模拟下部结构纵向刚度。以该模型计算温度、竖向活载和列车制动作用下单线单跨50 m简支梁桥上钢轨纵向力，与UIC774-3规范附录C2算例结果相比，钢轨应力相对误差为0.3%～4.9%，墩顶水平力相对误差为1.4%～7.4%，证明该模型可准确模拟桥梁和轨道之间的相互作用[11]。

以30 t轴重重载铁路双线32 m简支T梁为例，其截面形式如图1所示。

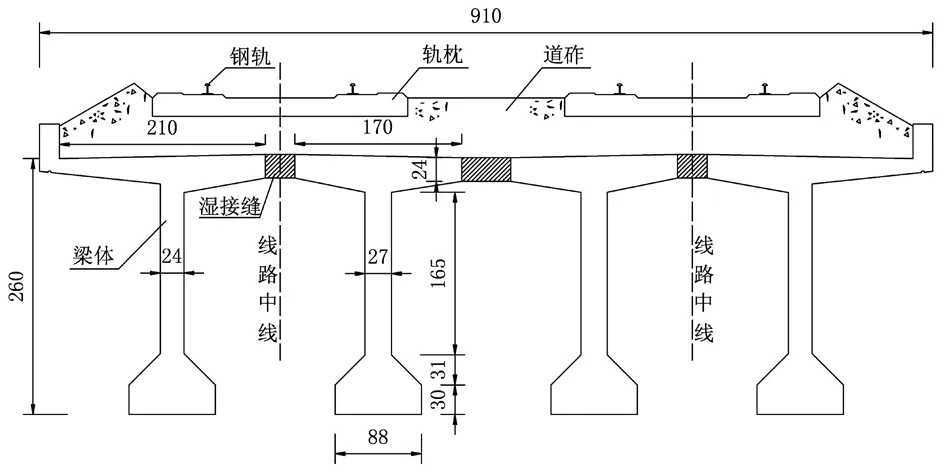
图1 重载铁路32 m简支T梁截面示意图Fig.1 Section of 32 m simply-supported T-beam for heavy haul railway(m)

建立11～32 m简支T梁桥-轨道系统地震响应仿真模型，其中：桥面铺装层、道砟、扣件等二期恒载按130 kN/m计；固定支座按线性弹簧处理；滑动支座采用理想弹塑性弹簧模拟，弹性阶段剪切刚度取为5.3 MN/m、弹塑性临界位移为9.3 mm；桥墩采用非线性梁单元以模拟可能出现的塑性变形，墩体混凝土取用Mander材料模型(无约束混凝土峰值应力为34 MPa，极限应变0.004，墩底塑性铰区截面配箍率0.004，纵向主筋配筋率0.03)，墩高统一取为20 m；墩底使用具有6个自由度的等效刚度矩阵模拟桩-土共同作用。在墩底支承点和路基支承点处建立大质量单元，释放支承点在激励方向上的约束，并在该点施加动力时程以模拟基础运动(质量取为结构总质量的1.0×108倍[12])，所建立的有限元模型如图2所示。

图2 重载铁路简支梁桥-轨道系统仿真模型Fig.2 Simulation model for bridge-track system

系统采用Rayleigh阻尼，阻尼比h取为0.05，阻尼系数α和β按式(2)取值：

(2)

式中：w1和w1为第一阶和对结构纵向振型贡献最大的一阶频率。

1.2 荷载参数的选取

在选取地震波时，将规范[13]反应谱导入美国加州大学伯克利分校开发的SIMQKE-GR软件生成人工波，将该人工波的反应谱与规范反应谱比较，使二者基本相符。按上述方法生成4类人工波作为地震激励，见表1。

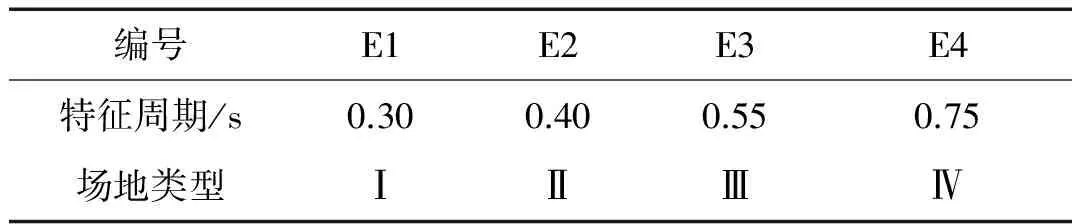
表1 本文所采用的人工波

地震设防烈度为8度，保留各地震波频谱特性，仅将各波最大峰值加速度调至0.3 g(设计地震)[13]。

进行地震动行波效应下系统动力响应分析时，仅考虑不同支承点输入时间上的差异，视波速取为200 m/s。

考虑温度效应时，采用考虑温度加载历史的荷载步法[14]，在梁体升降温15 ℃产生的温度变形的基础上进行地震激励。

在考虑列车制动作用时，参照文献[15]将30 t轴重重载铁路的重载等级系数取为1.2，即1.2倍ZH标准活载(图3)。假设列车以180 km/h的速度从P11台端驶入桥梁并制动，制动力率取为0.2[16]。

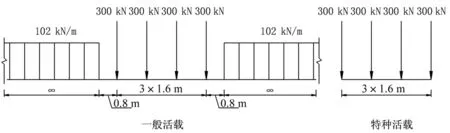
图3 30 t轴重重载铁路活载图式Fig.3 Live load diagram for 30t axle load railway

2 重载铁路简支梁桥-轨道系统主要设计参数

2.1 路基段钢轨长度

为考察路基段钢轨长度的影响，分别在桥梁两端路基上建立0～300 m钢轨，进行桥梁-轨道系统特征值及非线性时程分析，计算结果见图4。

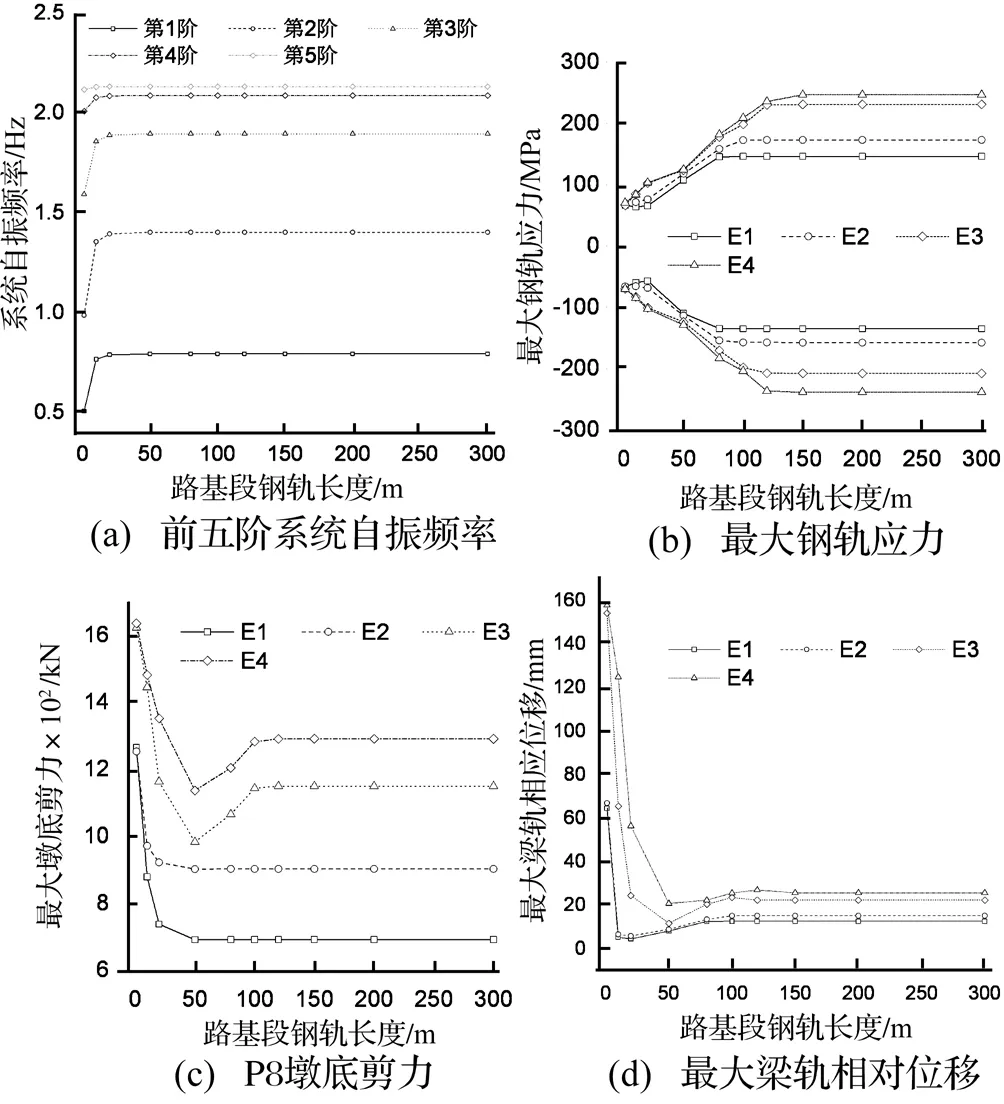
图4 路基段钢轨长度的影响Fig.4 Influence of track length on embankment

由图4可知，重载铁路简支梁桥-轨道系统地震响应对地震波频谱特性极为敏感，不同地震波作用下系统受力和变形在数值上存在显著差异。在考虑路基段钢轨后，相当于为桥梁结构增加了额外的纵向约束，可大幅度提高系统前3阶自振频率，改变结构振动特性。4种地震波作用下，当路基段钢轨长度超过110 m时，墩底剪力和梁轨相对位移最大值趋于稳定；超过130 m时，最大钢轨应力趋于稳定。

2.2 简支梁跨数

分别建立1～16跨32 m简支T梁桥-轨道系统仿真模型，计算系统自振频率及4种地震波作用下系统的动力响应，见图5。

图5 简支梁跨数的影响Fig.5 Influence of simply-supported bridge amount

随着简支梁跨数的增加，系统自振频率大幅度降低，钢轨应力、梁轨相对位移和台底剪力逐渐增加。当桥梁跨数超过10跨时，系统自振频率趋于定值；跨数超过8跨时，最大钢轨应力趋于定值。

2.3 滑动支座摩阻系数

将滑动支座摩阻系数分别取为0～0.07，研究其对系统地震响应的影响，见图6。

图6 滑动支座摩阻系数的影响Fig.6 Influence of sliding bearing friction factor

滑动支座摩阻系数对钢轨应力影响极小。随着摩阻系数的增大，墩底剪力分布更为均匀，梁轨相对位移和梁间相对位移均有不同程度的减小。

2.4 线路纵向阻力形式

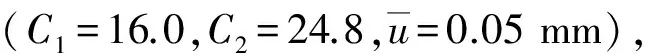
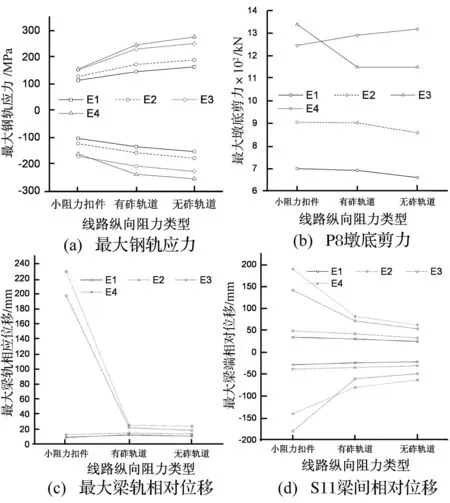
图7 线路纵向阻力的影响Fig.7 Influence of track longitudinal resistance

随着线路纵向阻力的提高，桥梁和轨道之间的相互作用增强，钢轨应力和墩底剪力有所增加，而梁轨相对位移和梁端位移差减小。由图7也可看出，在采用小阻力扣件时，梁间出现较大的相对位移，梁体将发生碰撞甚至落梁。

2.5 简支梁跨度

分别建立11跨20 m、24 m、32 m和40 m重载铁路简支梁-轨道系统模型，研究桥梁跨度对系统动力响应的影响，见图8。

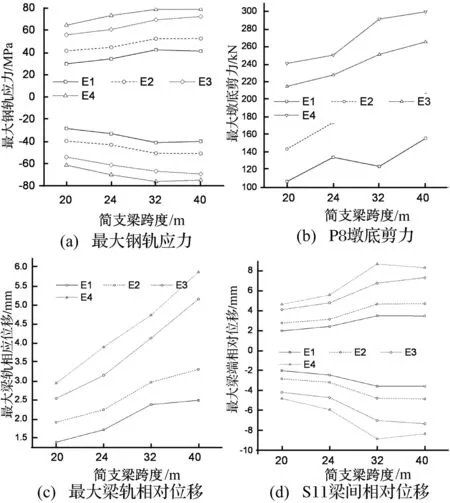
图8 简支梁跨度的影响Fig.8 Influence of simply-supported bridge span length

由于20～40 m简支梁跨度增幅不大，此范围内桥梁跨度对钢轨应力影响极小，但墩底剪力快速增大，桥梁跨度由32 m增加至40 m时，墩底剪力平均增大20%。

3 一致激励下简支梁-轨道系统地震响应

分别计算4种地震波(0.3 g，下同)作用下11～32 m重载铁路简支梁-轨道系统纵向受力及变形情况，见图9。

图9 纵向一致激励作用Fig.9 Longitudinal uniform excitation effect

由图9可以看出，地震波频谱特性对桥梁-轨道系统地震响应影响显著。一致激励作用下，钢轨应力包络图呈“双菱形”分布，钢轨最大应力均出现桥台附近(E4地震波作用下可达260.5 MPa)，各梁缝处钢轨受力亦较大。放置固定支座的桥台承受较大剪力，其余桥墩受力较为均衡。

与桥台相邻的第二跨简支梁梁缝处梁轨相对位移普遍较大(E4地震波作用下可达25.6 mm)，表明钢轨已发生快速滑移。与放置滑动支座的桥台相接的简支梁存在较大的纵向位移(E4地震波作用下达80.2 mm)，存在碰撞风险。

4 行波效应作用下简支梁-轨道系统地震响应

4.1 行波效应作用规律

设视波速为200 m/s，分别计算4种地震波作用下11～32 m重载铁路简支梁-轨道系统受力和变形情况，见图10。

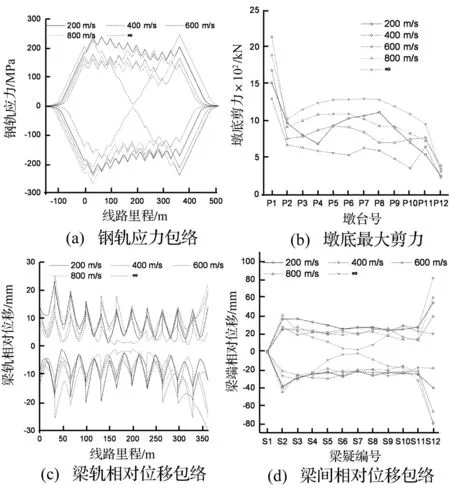
图10 纵向行波效应作用Fig.10 Longitudinal traveling wave effect

由图10可知，钢轨对纵向非一致激励极为敏感，与一致激励作用下的“双菱形”分布不同，行波效应下钢轨应力、梁轨相对位移和梁间相对位移分布均较为均匀。

4.2 视波速的影响

以E4地震波为例，分析视波速为200～800 m/s的行波效应和一致激励下，11～32 m重载铁路简支梁-轨道系统地震响应，见图11。

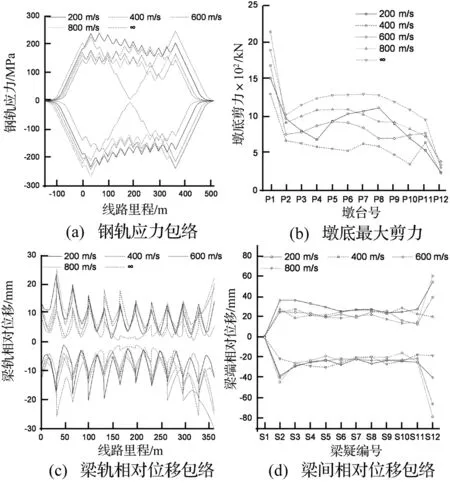
图11 视波速的影响Fig.11 Influence of apparent wave velocity

由图11可得，视波速对钢轨应力、墩底剪力、梁轨相对位移和梁间相对位移均有较大影响，且规律性并不明晰。总体而言，随着视波速的增加，系统的受力和变形逐渐接近一致激励下的情况。

5 温度、列车制动与地震的耦合作用

5.1 温度与地震耦合作用

在梁体升降温15℃的基础上，采用考虑加载历史的荷载步法分析E4地震波(0.3 g)作用下系统的动力响应。分析表明，考虑温度与否对钢轨应力和墩底水平力的影响极为微小，究其原因，笔者认为地震中钢轨单元受到反复动力作用(且数值大于钢轨伸缩力)，对钢轨应力产生耗散作用[17]。但梁体温度变形导致梁轨相对位移和梁间相对位移增大，一定程度上降低了钢轨的动力稳定，见图12。

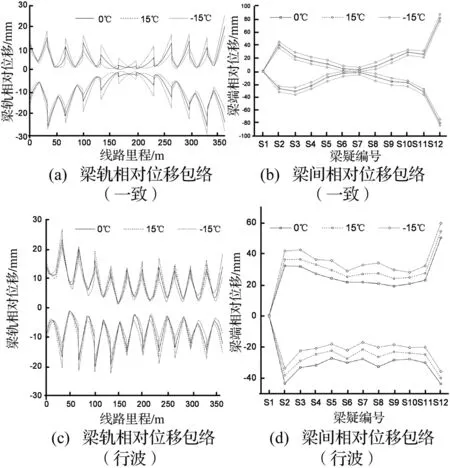
图12 温度与地震耦合作用Fig.12 Coupling effect of temperature and earthquake

5.2 列车制动与地震耦合作用

以E4波为例，假设(一致激励和行波效应)地震发生后第5 s、10 s和15 s时刻，列车从P11端入桥并制动，考虑列车竖向活载，制动力率取为0.25，系统动力响应见图13。

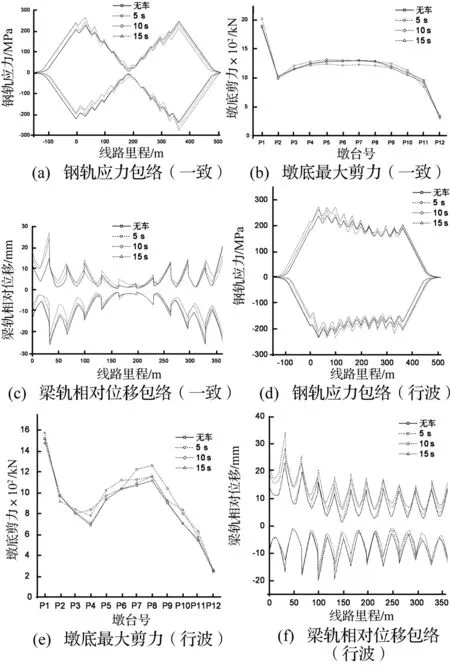
图13 列车制动和地震耦合作用Fig.13 Coupling effect of train brake and earthquake

由图13可以看出，不同时刻列车在桥上制动将一定程度上增大桥梁-轨道系统的受力和变形：某些区域钢轨应力可增大约53.6 MPa、墩底剪力增大215.8 kN、梁轨相对位移增大15.2 mm、梁间相对变形增大28.1 mm。

6 结 论

本文针对30 t轴重重载铁路桥梁，研究了一致激励和行波效应下重载铁路简支梁桥-轨道系统动力响应规律，并探讨了主要设计参数对系统响应的影响，得到的主要结论包括：

(1) 无缝线路的存在显著改变了重载铁路简支梁桥的自振特性，在进行铁路桥梁地震响应分析时，必须考虑桥上轨道结构的影响。

(2)当地形地质条件差别相差不大时，路基段钢轨长度可取为150 m、简支梁跨数可简化为11跨、滑动支座摩阻系数可取为0.03。

(3)线路纵向阻力对系统受力影响显著，线路阻力较小时，梁体与梁体、梁体与桥台间可能出现碰撞现象，甚至发生落梁。随着简支梁跨度的增加，墩底剪力快速增大。

(4)桥梁-轨道系统地震响应与地震频谱特性有关。总体而言，一致激励作用下，钢轨应力包络呈现“双菱形”分布，应力最大值出现在两端桥台处。某些情况下，梁轨快速相对位移可达25.6 mm，钢轨易发生动力失稳。

(5) 由于无缝线路轨道结构的纵向连续性，即使对于跨度较小的简支梁桥，也应考虑行波效应的影响，随着视波速的增加，钢轨应力和墩底剪力有所增加。

(6) 温度和列车制动作用增强了重载铁路简支梁桥-轨道系统的地震响应，进一步增大了轨道结构在地震中发生动力失稳的可能性。

[ 1 ] WU Qing, LUO Shihui, COLIN C.Longitudinal dynamics and energy analysis for heavy haul trains [J]. Journal of Modern Transportation, 2014, 22(3): 127-136.

[ 2 ] 杨德修. 重载铁路轨道技术发展方向研究 [J]. 铁道工程学报, 2012(2): 41-44. YANG Dexiu. Research on development direction of track technology of heavy-haul tailway [J]. Journal of Railway Engineering Society, 2012(2): 41-44.

[ 3 ] 戴福忠, 陈雅兰. 重载铁路桥梁设计列车标准活载的研究 [J]. 中国铁道科学, 2004, 25(4): 81-86. DAI Fuzhong, CHEN Yalan.Study on the standard live load of a train for the design of heavy load railway bridge [J]. China Railway Science, 2004, 25(4): 81-86.

[ 4 ] 王丽, 张玉玲. 新建重载铁路桥梁设计荷载标准的研究 [J]. 土木工程学报, 2013,46(3):103-109. WANG Li, ZHANG Yuling. Study on the design load model for new heavy haul railway bridges [J]. China Civil Engineering Journal, 2013, 46(3):103-109.

[ 5 ] 戴公连, 朱俊樸, 闫斌. 重载列车与既有铁路简支梁桥的适应性研究 [J]. 铁道科学与工程学报, 2014, 11(2): 7-13. DAI Gonglian, ZHU Junpu, YAN Bin. The adaptability research of heavy haul trains and existing railway simply-supported bridge [J]. Journal of Railway Science and Engineering, 2014,11(2): 7-13.

[ 6 ] 余志武, 李进洲, 宋力. 疲劳荷载后重载铁路桥梁剩余静载承载力试验研究 [J]. 铁道学报, 2014,36(4):76-85. YU Zhiwu, LI Jinzhou, SONG Li. Experimental study on post-cyclic-loading residual static bearing capacity of heavy-haul railway bridges [J]. Journal of the China Railway Society, 2014, 36(4):76-85.

[ 7 ] 戴公连, 朱俊樸, 闫斌. 30 t轴重重载铁路简支梁桥上无缝线路纵向力研究 [J]. 土木工程学报, 2015,48(8):1-10. DAI Gonglian, ZHU Junpu, YAN Bin. Longitudinal force of continuous welded rail on simply-supported bridge traveled by 30 t axle load heavy haul [J]. China Civil Engineering Journal, 2015, 48(8):1-10.

[ 8 ] EuroPean Committee For Standardization. Eurocaode 1:Actions on structures-Part 2:Traffic loads on bridges:BS EN 1991-2[S]. 2003.

[ 9 ] 铁路无缝线路设计规范:TB 10015—2012[S]. 北京: 中国铁道出版社, 2013.

[10] Track/bridge interaction. Recommendations for calculations:UIC. UIC 774-3 [S]. Paris: International Union of Railways, 2001. [11] 戴公连, 闫斌. 高速铁路斜拉桥与无缝线路相互作用研究 [J]. 土木工程学报, 2013,46(8):90-97. DAI Gonglian, YAN Bin. Interaction between cable-stayed bridge traveled by high-speed trains and continuously welded rail [J]. China Civil Engineering Journal, 2013.46(8): 90-97.

[12] YAN Bin, DAI Gonglian. Seismic pounding and protection measures of simply-supported beams considering interaction between continuously welded rail and bridge [J]. Structural Engineering International, 2013, 23(1):61-67.

[13] 中华人民共和国铁道部. 铁路工程抗震设计规范:GB 50111—2006[S]. 北京: 中国计划出版社, 2006.

[14] 闫斌, 戴公连. 考虑加载历史的高速铁路梁轨相互作用分析 [J]. 铁道学报, 2014,36(6):75-80. YAN Bin, DAI Gonglian. Analysis of interaction between continuously-welded rail and high-speed railway bridge considering loading-history [J]. Journalof the China Railway Society, 2014, 36(6): 75-80.

[15] 重载铁路设计规范(征求意见稿) [S]. 北京: 中国铁道出版社, 2011.

[16] 雷俊卿, 李宏年, 冯东. 铁路桥梁列车制动力的试验研究与计算分析 [J]. 工程力学, 2006,23(3):134-140. LEI Junqing, LI Hongnian, FENG Dong. Experimental study and computational analysis on braking force between running train and railway bridge [J]. Engineering Mechanics, 2006, 23(3):134-140.

[17] 闫斌. 高速铁路中小跨度桥梁与轨道相互作用研究 [D]. 长沙: 中南大学, 2013.

Seismic responses of a 30 t axle weight havey loaded railway simply-supported bridges-tracks system

YAN Bin1,2, PAN Wenbin1, LIU Shi1, DAI Gonglian1,2, WEI Biao1,2

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China)

In order to study seismic responses of a multi-span heavy loaded railway simply-supported bridges- tracks system, the validated bridge-track interaction analysis method was used to establish the simulation model of interaction between heavy loaded railway simply-supported bridges and double ballast tracks considering pile-soil interaction, pier elastic-plastic deformation, sliding bearing friction and track nonlinear resistance. The study revealed the seismic response law of the heavy loaded railway simply-supported bridges and tracks system under the seismic uniform excitation and traveling wave effect. The influences of design parameters, such as, track segment length, simply-supported bridge amount, span length, track longitudinal resistance form and sliding bearing friction coefficient were discussed. The stress characteristics of the system under the coupling effects among temperature, train brake and earthquake were analyzed. The results showed that when the geological conditions are similar, simply-supported bridges can be reduced to 11 spans and 150 m is taken as the length of track segment on embankment; when the track resistance decreases, both collision and beam falling may occur between beams and between abutment and beam; under longitudinal uniform excitation, the track stress envelope shape is a “double-diamond” with its maximum value appearing near the abutment, and the dynamic instability may occur due to larger track-bridge relative displacements near beam gaps; under the traveling wave effect, the stress and deformation laws of the system change significantly, so it is necessary to consider the effect of traveling wave even for smaller span simply-supported bridges; temperature and train braking action further increase the possibility of dynamic instability of the system under earthquakes.

heavy loaded railway; railway bridge; simply-supported beam; continuously welded rail; seismic response

高速铁路基础研究联合基金(U13342023); 中国铁路总公司科技研究开发计划课题(2015G001-G); 中国博士后科学基金资助项目 (2014M552158)

2015-08-05 修改稿收到日期：2016-01-09

闫斌 男，博士后，副教授，1984年生

魏标 男，副教授，1982年生

U213.912

A

10.13465/j.cnki.jvs.2017.03.030