基于A-T模型的长杆弹超高速侵彻陶瓷靶体强度分析
2017-03-09翟阳修
翟阳修, 吴 昊, 方 秦
(解放军理工大学 爆炸冲击防灾减灾国家重点实验室,南京 210007)
基于A-T模型的长杆弹超高速侵彻陶瓷靶体强度分析
翟阳修, 吴 昊, 方 秦
(解放军理工大学 爆炸冲击防灾减灾国家重点实验室,南京 210007)
Alekseevskii-Tate(A-T)模型广泛应用于长杆弹超高速冲击的终点效应分析中。A-T模型对于金属弹靶强度有明确的表达式,而对于陶瓷靶体强度尤其是弹体初始冲击速度大于1 500 m/s时还没有统一的结论。基于长杆钨弹超高速(1 500~5 000 m/s)侵彻三种陶瓷(AlN,B4C,SiC)/铝复合靶体的缩比逆弹道实验数据;基于A-T模型,给出了上述陶瓷材料在不同侵彻速度范围内的靶体强度表达式。进一步通过与47发长杆钨弹超高速(1 250~2 500 m/s)侵彻陶瓷(AlN,B4C,SiC,AD85)/RHA钢复合靶体DOP实验数据对比,验证了提出的陶瓷靶体强度表达式的适用性。
长杆弹;侵彻;陶瓷;强度;Alekseevskii-Tate模型
金属、陶瓷及其复合靶体具有优异的弹道性能,从而在武装直升机、军用车辆以及单兵防护系统中得到广泛应用。Alekseevskii-Tate(A-T)[1-2]模型对于长杆弹超高速冲击的终点效应有较好的预测,其核心问题在于弹靶强度的确定。对于金属弹靶材料强度,已有明确的表达式[3]。而由于脆性陶瓷材料成分复杂且制备工艺不同,使得在基于A-T模型进行长杆弹超高速冲击陶瓷靶体效应分析中,对于陶瓷强度的确定尚无统一的方法。
已有研究中,ROSENBERG等[4]基于对三种材料(铜、硬化钢、钨合金)弹体冲击AD85陶瓷靶体临界侵彻速度(侵蚀侵彻产生的临界速度)的实验研究,得出AD85陶瓷靶体强度可取其Hugoniot弹性极限(HEL)。并进一步得到4发长杆钨弹高速(1 122~1 400 m/s)侵彻AD85/RHA钢复合靶体DOP实验的验证,但该工作在实验发射次数和弹体冲击速度方面还存在局限。
TATE和STERNBERG[5]分别对长杆弹超高速冲击作用下陶瓷材料阻力进行分析,认为A-T模型中陶瓷靶体强度等于弹体侵入靶体形成空腔的径向准静态膨胀压力。FORRESTAL等[6-8]进一步基于静态球形空腔膨胀理论(空腔膨胀压力与膨胀速度无关),分别针对弹体超高速冲击作用下靶体不同的响应分区(弹性-开裂-塑性,弹性-塑性,弹性-开裂-破碎),对AD85和AD995陶瓷的A-T模型强度进行了分析。魏雪英等[9-10]针对弹性-开裂-破碎的靶体响应分区,分别基于静态球形和柱形空腔膨胀理论对陶瓷靶体强度进行分析,并对长杆钨弹侵彻AlN陶瓷靶体的侵彻深度进行了预测对比。李金柱等[11]基于静态球形空腔膨胀理论得到陶瓷靶体强度随弹体速度增大而减小的结论,并进一步认为陶瓷材料平均阻抗可用于侵彻深度的计算。
为了进一步表征不同速度弹体冲击作用下,靶体开裂程度引起的靶体强度变化。基于动态空腔膨胀理论(空腔膨胀压力与膨胀速度相关),KARTUZOV等[12-13]分别基于弹性-开裂-破碎靶体响应分区对AD995陶瓷靶体强度进行了讨论。SATAPATHY进一步发现陶瓷靶体强度在弹体冲击速度大于3 000 m/s时出现显著下降。
虽然基于空腔膨胀理论可以得到任意冲击速度下陶瓷靶体的强度,且具有较高的预测精度。但其应用往往需要开展包括一维平板撞击在内的多个静动力实验来确定靶体材料压剪系数、体积模量、抗压和抗拉强度等一系列物理力学参数,无法满足工程设计快速计算的需要。
本文基于ORPHAL等[14-16]开展的长杆钨弹超高速(1 500~5 000 m/s)侵彻三种陶瓷(AlN,B4C和SiC)/铝复合靶体的缩比逆弹道实验,给出了上述陶瓷材料在不同弹体冲击速度范围的A-T模型靶体强度的显式表达式。并与FRANZEN等[17-19]开展的47发长杆钨弹超高速(1 250~2 500 m/s)侵彻后覆RHA钢的四种陶瓷(AlN,B4C,SiC和AD85)靶体DOP实验数据进行了对比。
1 A-T模型[1-2]
TATE和ALEKSEEVSKII在一维流体Bernoulli方程中引入弹体和靶体强度参数Yp和Rt,建立了长杆弹超高速侵彻金属靶体时弹靶交界面轴向应力平衡关系,即一维半流体动力学Alekseevskii-Tate(A-T)模型,
(1)
式中:ρp和ρt分别为弹体和靶体材料的密度。v和u分别为弹体尾部的瞬时刚性侵彻速度和弹体头部(弹靶接触界面)的瞬时侵彻速度。
A-T模型假设高速侵彻过程中弹靶接触界面区域呈流体状态,弹体发生侵蚀,控制方程为:
(2)
(3)
(4)
式中:P和l分别为弹体的瞬时侵彻深度和长度。
对于金属材料,弹靶强度Yp和Rt的确定已有公认的结论
(5)
式中:σyp和σyt分别为弹体和靶体材料的静态屈服强度,Et为靶体材料的弹性模量。
2 陶瓷靶体强度Rt确定
2.1 实验
ORPHAL等开展了长杆钨弹超高速(1 500~ 5 000 m/s)侵彻AlN、B4C和SiC三种陶瓷/铝复合靶体的缩比逆弹道实验,得到了弹体的无量纲侵彻深度P/L,其中P为实验侵彻深度,L为弹体初始长度。图1和图2分别给出了上述实验示意图以及弹体无量纲侵彻深度的实验数据。

图1 长杆弹超高速侵彻陶瓷靶体缩比逆弹道实验示意图Fig.1 Scheme of reduce-scaled reverse ballistic test of long-rod projectile hypervelocity penetrating into ceramic target(mm)

图2 长杆弹超高速侵彻陶瓷靶体无量纲侵彻深度Fig.2 Penetration tests data P/L of ceramic target against hypervelocity penetration of long-rod projectile
2.2 模型求解与陶瓷靶体强度确定
基于MATLAB软件对A-T模型进行数值求解。弹体在t时刻的瞬时刚性侵彻速度、侵彻深度和长度分别为vt、Pt和lt。基于式(2)求得弹体瞬时刚性侵彻速度变化量dv,进而得到t+1时刻的弹体瞬时刚性侵彻速度vt+1=vt+dv。基于vt+1和式(1)求得t+1时刻的弹体瞬时侵彻速度u,将u代入式(3)、(4)分别求得弹体瞬时侵彻深度和长度的变化量dP和dl,进而得到t+1时刻的弹体瞬时侵彻深度与长度分别为Pt+1=Pt+dP和lt+1=lt+dl。初始条件为t=0时,v=V0,P=0,l=L。循环以上计算过程直至上述变量满足条件v
对于图1所示的陶瓷/金属复合靶体,将长杆钨弹贯穿3.18 mm金属盖板后的瞬时刚性侵彻速度和瞬时长度作为侵彻陶瓷靶体的初始条件。基于A-T模型对弹体冲击金属盖板和陶瓷靶体分别计算,其中金属材料弹靶强度由式(5)给出。

图3 A-T模型求解流程图Fig.3 Flow chart based on A-T model
基于图2中弹体无量纲侵彻深度实验数据和图3给出的计算流程,得到弹体不同初始冲击速度下三种陶瓷靶体的强度值Rt如图4所示。

(a) AlN (b) B4C (c) SiC图4 三种陶瓷靶体强度值Rt与弹体冲击速度V0的关系Fig.4 Relationship of Rt and V0 of three ceramic targets
从图4可以看出,当弹体冲击速度V0小于3 000 m/s时,三种陶瓷靶体强度值Rt没有明显的下降。当弹体冲击速度V0大于3 000 m/s时,靶体材料行为趋于流体,Rt值下降趋势明显,这与SATAPATHY[13]结论一致。为方便快速工程计算,对上述三种陶瓷靶体强度值Rt确定如下:
1)当弹体冲击速度满足V0小于1 500 m/s时,结合ROSENBERG[4]工作,认为陶瓷靶体强度值Rt近似取陶瓷材料的HEL。
2)当弹体冲击速度V0在1 500~3 000 m/s时,取该速度范围内Rt值的平均值,如图4所示,对于上述三种陶瓷靶体,有:
Rt(AlN)=7.04 GPa
(7a)
Rt(B4C)=6.25 GPa
(7b)
Rt(SiC)=8.89 GPa
(7c)
式(7a)与魏雪英等[9]基于静态球形空腔膨胀理论得到的AlN陶瓷靶体强度为7.02 GPa和SATAPATHY[13]基于动态球形空腔膨胀理论得到的AlN陶瓷靶体强度为7 GPa基本一致。
3)当弹体冲击速度V0在3 000~5 000 m/s时,对Rt值进行线性拟合,如图4所示,得到:
Rt(AlN)=-0.004 7V0+21.12 GPa
(8a)
Rt(B4C)=-0.002 6V0+14.06 GPa
(8b)
Rt(SiC)=-0.005 1V0+24.13 GPa
(8c)
4)当弹体冲击速度V0大于5 000 m/s时,陶瓷靶体可按流体处理,靶体强度值Rt=0。
2.3 靶体强度验证
弹体冲击速度在1 500~3 000和3 000~5 000 m/s时,陶瓷靶体强度Rt分别由式(7)和式(8)给出。基于A-T模型和图3给出的求解流程计算得到的弹体无量纲侵彻深度P/L与ORPHAL等实验数据对比如图5和图6所示。图5和图6同时给出计算结果±10%的误差范围,可以看出90%的预测结果误差均小于10%。

(a) AlN (b) B4C (c) SiC图5 计算结果与实验数据对比(1 500~3 000 m/s)Fig.5 Comparisons of calculate results and tests data (1 500~3 000 m/s)

(a) AlN (b) B4C (c) SiC图6 计算结果与实验数据对比(3 000~5 000 m/s)Fig.6 Comparisons of calculate results and tests data (3 000~5 000 m/s)
3 实验对比
终点效应研究中较多采用DOP(Depth of Penetyation)实验来定量衡量某种陶瓷靶体的抗弹体冲击能力,图7给出了DOP实验示意图。本节进一步基于FRANZEN等开展的陶瓷/RHA钢复合靶体DOP实验对上节给出的陶瓷靶体强度表达式进行验证。表1给出了上述实验的弹靶材料及其A-T模型参数。
3.1 FRANZEN等实验
FRANZEN等进行了长杆钨弹超高速(1 500~ 2 500 m/s)侵彻AlN/RHA钢和SiC/RHA钢复合靶体

表1 弹靶参数
的DOP实验。基于A-T模型和表1中参数计算得到的弹体无量纲侵彻深度P/L与实验数据对比如图8所示。图8同时给出了计算结果±10%的误差范围。
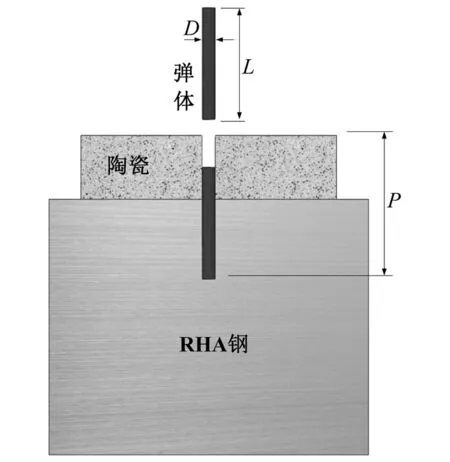
图7 DOP实验示意图Fig.7 Scheme of DOP test
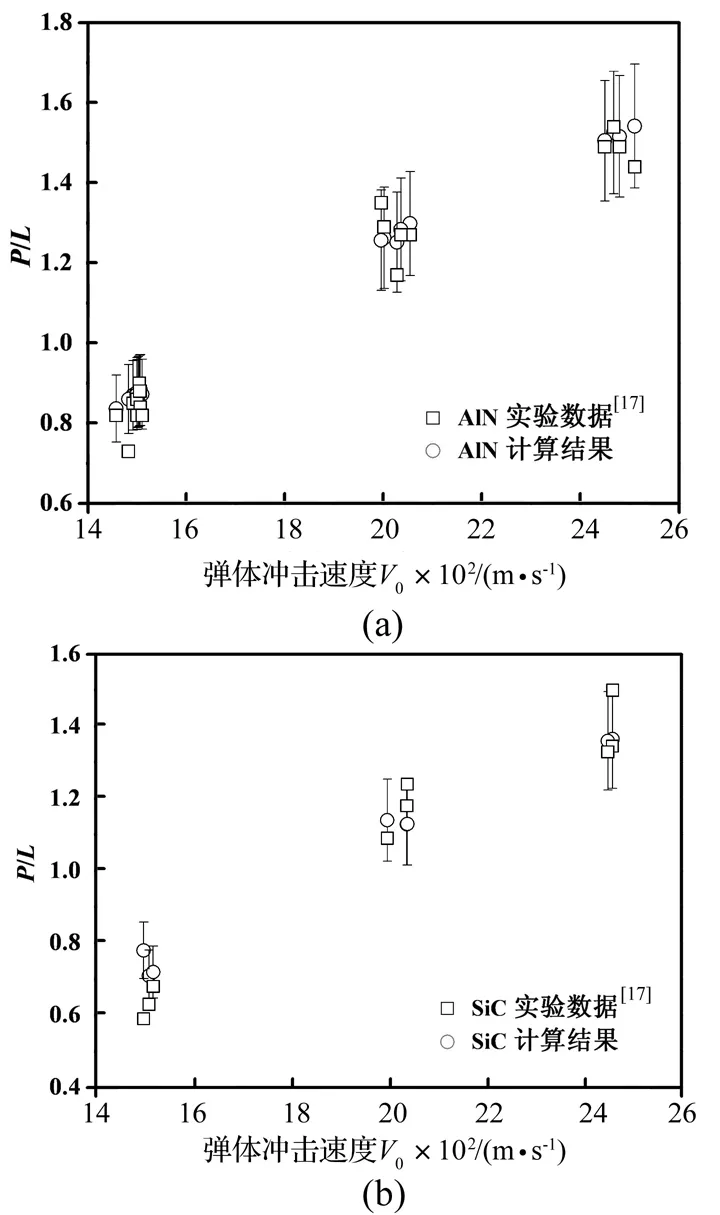
图8 弹体无量纲侵彻深度计算结果与实验数据对比Fig.8 Comparisons of calculate results and tests data of P/L
3.2 ROSENBERG等实验
ROSENBERG等开展了钨合金长杆弹近似1 250 m/s速度冲击三种厚度(19.8 mm,39.6 mm和59.8 mm)AD85陶瓷/RHA钢复合靶体的DOP实验,弹靶参数见表1所示。基于A-T模型计算得到的弹体无量纲侵彻深度P/L与实验数据对比如图9所示。

图9 弹体无量纲侵彻深度计算结果与实验数据对比Fig.9 Comparison of calculate result and test data of P/L
ROSENBERG等[19]开展了钨合金长杆弹超高速(1 700 m/s)侵彻后覆RHA钢的不同厚度陶瓷(AlN,B4C,SiC)复合靶体DOP实验,弹靶参数见表1所示。基于A-T模型计算得到的弹体无量纲侵彻深度P/L与实验数据对比如图10所示。

图10 弹体无量纲侵彻深度计算结果与实验数据对比Fig.10 Comparisons of calculate results and tests data of P/L
从图8~图10可以看出,当陶瓷靶体强度值Rt由式(7)确定时,基于A-T模型计算得到的92%的预测结果误差均小于10%,从而验证了上节给出的陶瓷靶体强度表达式的正确性和适用性。
4 结 论
本文基于A-T模型和ORPHAL等开展的长杆钨弹对三种陶瓷复合靶体超高速缩比逆弹道侵彻实验,给出了方便工程快速计算的陶瓷靶体强度值Rt的显式表达式,并得到实验验证。主要结论有:
(1)弹体侵彻金属靶体的一维经典A-T理论模型同样可用于陶瓷靶体抗弹体超高速冲击的终点效应分析中;
(2)弹体冲击速度小于1 500 m/s时,陶瓷靶体强度Rt取其HEL;弹体冲击速度在1 500~3 000 m/s时,三种陶瓷靶体强度的建议取值分别为Rt(AlN)=7.04 GPa,Rt(B4C)=6.25 GPa和Rt(SiC)=8.89 GPa;
(3)弹体冲击速度在3 000~5 000 m/s时,给出了与冲击速度相关的陶瓷靶体强度表达式。计算得到的预测结果与ORPHAL等实验数据有较好的吻合性。但因缺乏更多的实验数据,该速度范围内Rt表达式的适用性有待进一步实验验证。
[ 1 ] TATE A. A theory for the deceleration of long rods after impact [J]. Journal of Mechanics and Physics of Solids, 1967, 15(6): 387-399.
[ 2 ] ALEKSEEVSKII V P. Penetration of a rod into a target at high velocity [J]. Combustion Explosion and Shock Waves, 1966, 2(2): 63-66.
[ 3 ] TATE A. Long rod penetration models-partII. Extensions to the hydrodynamic theory of penetration [J]. International Journal of Mechanical Sciences, 1986, 28(9): 599-612.
[ 4 ] ROSENBERG Z, TSALIAH J. Applying Tate’s model for the interaction of long rod projectiles with ceramic targets [J]. International Journal of Impact Engineering, 1990, 9(2): 247-251.
[ 5 ] STERNBERG J. Material properties determining the resistance of ceramics to high velocity penetration [J]. Journal of Mechanics and Physics of Solids, 1989, 65(9): 3417-3424.
[ 6 ] FORRESTAL M J, LONGCOPE D B. Target strength of ceramic material for high-velocity penetration [J]. Journal of Applied Physics, 1990, 67(8): 3669-3672.
[ 7 ] PARTOM Y, LITTLEFIELD D L. Dependence of ceramic armor resistance on projectile velocity [C]// The 14thInternational Symposium on Ballistic, Quebec, 1993, 563-572.
[ 8 ] SATAPATHY S, BLESS S. Calculation of penetration resistance of brittle materials using spherical cavity expansion analysis [J]. Mechanics of Materials, 1996, 23(96): 323-330.
[ 9 ] 魏雪英, 俞茂宏. 钨杆弹高速侵彻陶瓷靶的理论分析 [J]. 兵工学报, 2002, 23(2): 167-170. WEI Xueying, YU Maohong. Analysis of tungsten rods on penetrating ceramictargets at high velocity [J]. Chinese Acta Armamentarii, 2002, 23(2): 167-170.
[10] 王延斌, 李九红, 魏雪英, 等. 高速钨杆弹对脆性靶体的侵彻分析 [J]. 高压物理学报, 2005, 19(3): 257-263. WANG Yanbin, LI Jiuhong, WEI Xueying, et al. Analysis of high-velocity tungsten rod on penetrating brittle target [J]. Chinese Journal of High Pressure Physics, 2005, 19(3): 257-263.
[11] 李金柱, 黄风雷, 张连生. 陶瓷材料抗长杆弹侵彻阻抗研究 [J]. 北京理工大学学报, 2014, 34(1): 1-5. LI Jinzhu, HUANG Fenglei, ZHANG Liansheng. Penetration resistance of ceramic materials subjected to projectile’s impact [J]. Transactions of Beijing Institute of Technology, 2014, 34(1):1-5.
[12] KARTUZOV V V, GALANOV B A, IVANOV S M. Concept of ultimate fracture velocity in the analysis of spherical cavity expansion in brittle materials: application to penetration problems [J]. International Journal of Impact Engineering, 1999, 23(1): 431-442.
[13] SATAPATHY S. Dynamic spherical cavity expansion in brittle ceramics [J]. International Journal of Solids and Structure, 2001, 38: 5833-5845.
[14] ORPHAL D L, FRANZEN R R, PIEKUTOWSKI AJ, et al. Penetration of confined aluminum nitride targets by tungsten long rods at 1.5-4.5 km/s [J]. International Journal of Impact Engineering, 1996, 18(95): 355-368.
[15] ORPHAL D L, FRANZEN R R, CHARTERS A C, et al. Penetration of confined boron carbide targets by tungsten long rods at impact velocities from 1.5 to 5.0 km/s [J]. International Journal of Impact Engineering, 1997, 19(96): 15-29.
[16] ORPHAL D L, FRANZEN R R. Penetration of confined silicon carbide targets by tungsten long rods at impact velocities from 1.5-4.6 km/s [J]. International Journal of Impact Engineering, 1997, 19(1): 1-13.
[17] FRANZEN R R, ORPHAL D L, ANDERSON C E. The influence of experimental design on Depth-Of-Penetration (DOP) test results and derived ballistic efficiencies [J]. International Journal of Impact Engineering, 1997, 19(8): 727-737.
[18] ROSENBERG Z, DEKEL E, HOHLER V, et al. Hypervelocity penetration of tungsten alloy rods into ceramic tiles: experiment and 2-D simulations [J]. International Journal of Impact Engineering, 1997,20: 675-683.
[19] ROSENBERG Z, DEKEL E, HOHLER V, et al. Penetration oftungsten-alloy rods into composite ceramic targets: Experiment and 2-D simulations [C]//The tenth American Physical Society topical conference on shock compression of condensed matter. AIP Publishing, 1998, 429(1): 917-920.
Strength analysis of ceramic targets against hypervelocity penetration of long-rod projectiles based on A-T model
ZHAI Yangxiu, WU Hao, FANG Qin
(State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact, PLA University of Science and Technology, Nanjing 210007, China)
Alekseevskii-Tate (A-T) model is widely used in the terminal ballistic analysis of long-rod projectiles’ hypervelocity penetrations. The explicit expressions for both strengths of metallic projectile and target in a A-T model were proposed previously. However, there was no uniform conclusion for the strength of ceramic targets in a A-T model, especially, when the initial impact velocity of projectiles was larger than 1 500 m/s. Based on reduce-scaled reverse ballistic test data of long-rod tungsten projectiles’ hypervelocity (1 500~5 000 m/s) penetrating into three ceramic (AlN, B4C, SiC)/aluminum composite targets, by using A-T model, the expressions of the above three ceramic targets’ strengths under various projectile impact velocities were obtained. Furthermore, by comparing the above test data with the DOP tests data of 47 long-rod tungsten projectiles’ hypervelocity (1 250~2 500 m/s) penetrating into ceramic (AlN, B4C, SiC, AD85)/RHA steel blocks targets, the applicability of the proposed expressions of ceramic strength were validated.
long-rod projectile; penetration; ceramic; strength; Alekseevskii-Tate (A-T) model
国家自然科学创新研究群体基金(51321064);国家自然科学基金(51522813)
2016-01-05 修改稿收到日期:2016-06-22
翟阳修 男,硕士生,1991年生
吴昊 男,博士,副教授,1981年生
O348
A
10.13465/j.cnki.jvs.2017.03.029
