基于改进MP的稀疏表示快速算法及其滚动轴承故障特征提取应用

王 林, 蔡改改, 高冠琪, 周 菲, 杨思远, 朱忠奎

(苏州大学 城市轨道交通学院 苏州 215131)

基于改进MP的稀疏表示快速算法及其滚动轴承故障特征提取应用

王 林, 蔡改改, 高冠琪, 周 菲, 杨思远, 朱忠奎

(苏州大学 城市轨道交通学院 苏州 215131)

在恒定转速情况下，旋转机械中滚动轴承的局部故障往往导致周期性冲击，从而产生周期性瞬态振动信号。对局部故障的瞬态特征提取一直是故障检测的关键问题。基于匹配追踪(Matching Pursuit, MP)算法的稀疏分解是一种信号自适应分解算法，是强噪声背景下微弱特征提取的有效方法之一。针对滚动轴承故障振动信号稀疏表示过完备字典的选择与构造问题，基于相关滤波法优选与冲击波形匹配的Laplace小波原子构造稀疏表示中的过完备字典；针对基本匹配追踪算法计算量大、效率低的问题，结合FFT快速运算特性，通过互相关运算替换基本匹配追踪算法中的内积运算，研究基于改进MP的稀疏表示快速算法，进而提高计算效率。仿真与滚动轴承故障实验分析结果表明该算法能准确的提取滚动轴承故障特征且计算效率高。

滚动轴承；匹配追踪；字典构造；FFT；特征提取

作为机械设备的关键零部件，滚动轴承往往长期运转于高温、高压及复杂的力学环境下，极易发生故障。以航空发动机为例，高压压气机前轴承失效是致使发动机空中停车的主要原因之一，而航空发动机中的中介轴承一旦失效，会在极短时间内导致发动机主轴抱轴裂断，因此，对滚动轴承的运行状态进行监测与诊断至关重要。运转中的滚动轴承一旦发生故障，其振动信号中将会出现周期性的冲击成分，致使滚动轴承的振动信号出现调制现象。尤其是在故障初期，冲击成分往往比较弱，加之受到周围噪声干扰，致使微弱的故障特征难以提取。因此，如何有效提取滚动轴承微弱故障特征是滚动轴承故障诊断的关键，对保障滚动轴承的安全可靠运行具有重要意义。

在滚动轴承故障诊断方面，大量的非平稳信号分析方法如短时傅里叶变换[1],小波变换[2-4],经验模态分解[5-6],EEMD算法[7-8]等被提出并取得良好的应用效果。稀疏分解的思想最早可追溯到MALLAT等[9]基于过完备冗余字典库所提出的匹配追踪方法，该方法通过在过完备库中自适应地选择与信号最相似的原子，并使选择的原子个数尽可能的少，从而得到原始信号非常简洁的表示，即稀疏表示。稀疏表示能够在稀疏正则化约束下对复杂信号进行变换和分解，它通过设计超完备字典并构造合适的目标函数，优化求解得到复杂信号在超完备字典中的稀疏解，用较少的变换系数就可以刻画信号本质。稀疏表示一经提出，便以其良好的特性引起诸多领域如图像处理、人脸识别、生物信号处理、特征提取等研究人员的广泛关注。其中基于匹配追踪(MP)的稀疏分解是稀疏表示算法中最常用的方法之一。在机械设备故障诊断领域，诸多学者也对相关算法做了大量的研究和改进工作，并获得了较好的应用效果。CUI等[10]结合故障产生机理，提出了基于自适应冲击字典的匹配追踪稀疏表示算法，并成功应用于滚动轴承故障诊断。周凤星等[11]研究了基于相干累积量分段正交匹配追踪方法的轴承早期故障特征稀疏表示方法。CAI等[12]针对齿轮故障信号的特点，提出基于可调Q因子小波变换的稀疏分解算法。尽管基于匹配追踪的稀疏分解算法在信号自适应分解方面取得良好的效果，然而在基于匹配追踪的信号稀疏分解过程中，每一步都要进行信号或残差信号在过完备字典库中每一个字典上的内积计算，这势必带来巨大的运算量，影响算法效率。此外，在基于匹配追踪的稀疏分解算法中，过完备字典的选取及构造也直接决定了算法对信号稀疏表示的效果。

本文针对滚动轴承故障振动信号稀疏表示过完备字典的选择与构造问题，通过相关滤波法优选与冲击信号波形匹配的Laplace小波原子构造过完备字典，提高轴承故障振动信号稀疏表示的效果；针对基于匹配追踪的稀疏表示算法计算量大，算法效率低的问题，利用快速傅里叶变换(FFT)快速计算的特性实现快速互相关运算，替换原始算法中的内积运算，提高算法运算速度。仿真分析及实验表明所研究方法既能实现滚动轴承故障信号中冲击成分的更佳稀疏表示，又能显著提高计算效率，能快速有效地将滚动轴承信号中的微弱冲击成分提取出来。

1 基于FFT的改进MP算法

匹配追踪(MP)算法是MALLAT等于1993年提出的一种迭代算法，在进行每一次迭代时，挑选过完备原子库(或冗余字典)中与输入信号结果最为匹配的原子，达到对信号的一种逼近。

目前MP稀疏表示在信号处理的实际应用中遇到较大障碍，关键问题之一在于信号稀疏分解的计算量十分巨大。国内有研究人员指出，当信号长度为1024时，信号稀疏分解的难度将十分巨大[13]。MP稀疏表示算法的计算量一方面受过完备原子库结构特性的影响，另一方面则是由于在该稀疏表示过程中，要进行多次内积运算，且每次运算都是在高维空间进行的。为解决上述问题，本文从以下两个方面考虑，一方面，如果构建的字典中的原子与待分析信号的主要成分相似，就不必构造大量的原子，可直接选取与其较为相似的一系列原子进行分解重构，因此针对滚动轴承故障振动信号特点，本文选取与轴承故障振动信号较为相似的Laplace小波基作为过完备原子库；另一方面，为解决内积运算速度较慢的问题，利用FFT快速计算的特性，将内积运算转换为利用FFT实现互相关运算，用FFT来降低运算复杂度，进而在性能不变的情况下，有效降低运算复杂度，提高运算速度。

假设原子库中的原子由参数(ui,vi,ωi,si)所确定，由文献[13]知，在稀疏分解的过程中，如果对原子库中的某一原子参数(vi,ωi,si)的选取方法保持不变，可以取u=N/2,通过平移就可以得到参数为(si,vi,ωi,ui)的原子(ui≠N/2)，为了不影响稀疏分解结果，u取所有可能的值[0∶N-1]。对于具有参数(si,vi,ωi)的一个原子gγ，这个原子要和残余信号做N次内积运算。由于ui从0到N-1连续取值，从理论上讲，所有的N次内积运算〈Rkf,gγk〉可以转换为两个向量Rkf和gγk的一次互相关运算。在寻找内积最大值的过程实际上就是寻找互相关最大值的过程，原子平移的运算量是可以忽略不计的，因此，既可以减少原子生成的时间，也可以减少存储空间，进而达到较好的折中。

此外，利用FFT可以实现互相关运算，对上述算法进一步改进，这种改进不会影响稀疏分解的效果，却可以大大提高稀疏分解的速度。

对于信号g、SR，其互相关函数定义为R=g*SR，对互相关函数R做FFT变换，即fft(R)=fft(g*SR)=fft(g)×fft(SR)。那么R=ifft(fft(g)×fft(SR))，具体过程如图1所示。图中g为冗余字典中的原子，SR是信号或信号残差的反转序列，Co为这个子集所对应的投影系数值，也即为g、SR的互相关运算值R。

图1 FFT实现互相关过程Fig.1 Implementation of cross-correlation with FFT

2 基于改进MP的稀疏表示快速算法

在恒定转速情况下，旋转轴承的局部故障往往导致周期性冲击，从而产生周期性瞬态冲击成分，且由轴承故障引起的瞬态冲击成分一般呈现接近单边振荡衰减的波形。

Laplace小波是一种单边衰减的复指数小波，訾艳阳等给出了Laplace小波的数学表达式，考虑到实际采集信号多为实信号，本文采用Laplace小波实数形式，

D(t,τ)=ψ(t,τ,ζ,f)=

(1)

式中:f为衰减频率,ζ为黏滞阻尼比,τ为时延,WS为支撑区间,A用来归一化小波函数。

Laplace小波与滚动轴承故障振动信号特征极为相似，故本文选取Laplace小波作为稀疏表示过完备字典中的原子。过完备原子库D由不同参数(τ,f,ζ)的Laplace小波构成，利用相关滤波法确定ζ的取值范围，优选与轴承瞬态成分最相似的小波原子[14-15]。f由故障信号频谱峰值确定，τ与时间t变化范围相同，以此形成的过完备原子库中每个原子与轴承故障信号中的瞬态冲击响应成分匹配度较高，用该字典D来进行稀疏表示，字典中的原子与噪声匹配度较低，用该方法可以有效的消除噪声的干扰。

利用上述方法生成字典D，对轴承故障振动信号进行基于FFT互相关的匹配追踪，得到各匹配时刻，各投影系数之间时间间隔即为故障周期，同时对重构信号进行包络分析也可以得到故障周期。具体算法流程如图2所示。

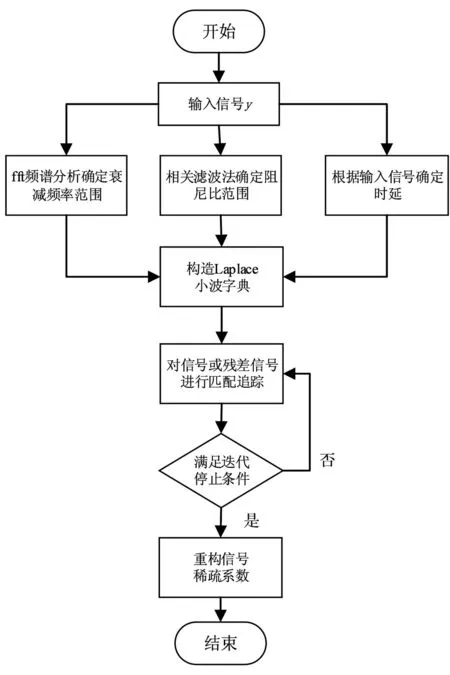
图2 基于改进MP的稀疏表示快速算法Fig.2 The fast algorithm of sparse representation based on improved MP

为验证本文方法的有效性及优越性，首先用仿真信号进行分析说明。考虑到滚动轴承出现故障时其振动响应信号特点，构造如式(2)所示的仿真信号来模拟轴承故障振动信号。

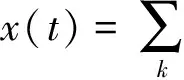
(2)

式中:t∈[0,1] s，f0=300 Hz，ζ0=0.05，τ0=0.05 s，T0=0.1 s，n(t)为白噪声，An为噪声幅值，取An=0.25 m/s2，采样频率为2 000 Hz。

利用本文方法对该仿真信号进行分析，验证该方法对冲击时刻的辨识能力。轴承故障仿真信号如图3(a)所示，对仿真信号进行FFT频谱分析如图3(b)所示，得到峰值频率f=299.9 Hz，确定冲击衰减频率变化区间。通过相关滤波确定最佳阻尼比为ζ0=0.05。对仿真信号进行稀疏表示，迭代10次得到重构信号结果如图3(d)所示，迭代时间为1.98 s。由图3(c)稀疏系数得到冲击时刻，根据相邻主要响应成分的时间间隔Δt的平均值得到周期T，从图3(c)中可得到T=0.1 s，与设定值相同。在仿真过程中，字典D中的原子与冲击成分相似度很高，几次迭代就可以得到原始信号的主要冲击成分，过多的迭代次数则会引入噪声成分，为避免该情况发生，本文通过设置阈值co来确定迭代次数,

(3)

式中:rformer表示前一次信号残差，rafter表示后一次信号残差。

相关系数可用于评价两信号或矢量之间的相似程度，利用重构信号与仿真信号的相关系数(Correlation Coefficient, CC)来评判重构信号的优劣程度，相关系数用内积定义如下：

(4)

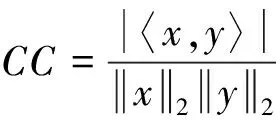
(5)

相关系数越接近1，表明重构信号与原信号相关程度越大，重构性能越好。

对图3(a)和3(e)信号做相关计算得相关系数为0.986 4，表明该方法的重构性能较好，且能够确定周期性冲击信号的周期成分。

为进一步验证该方法的微弱故障特征提取能力，进一步增大白噪声幅值An=0.4 m/s2进行分析，仿真信号、频谱、稀疏系数、重构信号如图4所示。

从图4(c)可以得到周期性冲击信号的平均周期T=0.1 s，与设定值相同，由此可见，在信噪比较低情况下，所提出方法依旧能够获得良好的分析效果。为进一步验证本文算法相较于MP基本算法在运算效率上的优势，分别利用两算法对仿真信号进行分析。图5(a)所示为轴承故障仿真信号，图5(b)、5(c)分别为改进算法和MP基本算法稀疏重构结果。MP基本算法根据MP迭代计算过程编写，通过内积运算匹配最佳原子。在相同条件下，运算时间如表1所示，从表1可以看出在重构效果相似情况下，本文算法运算效率有明显提高。

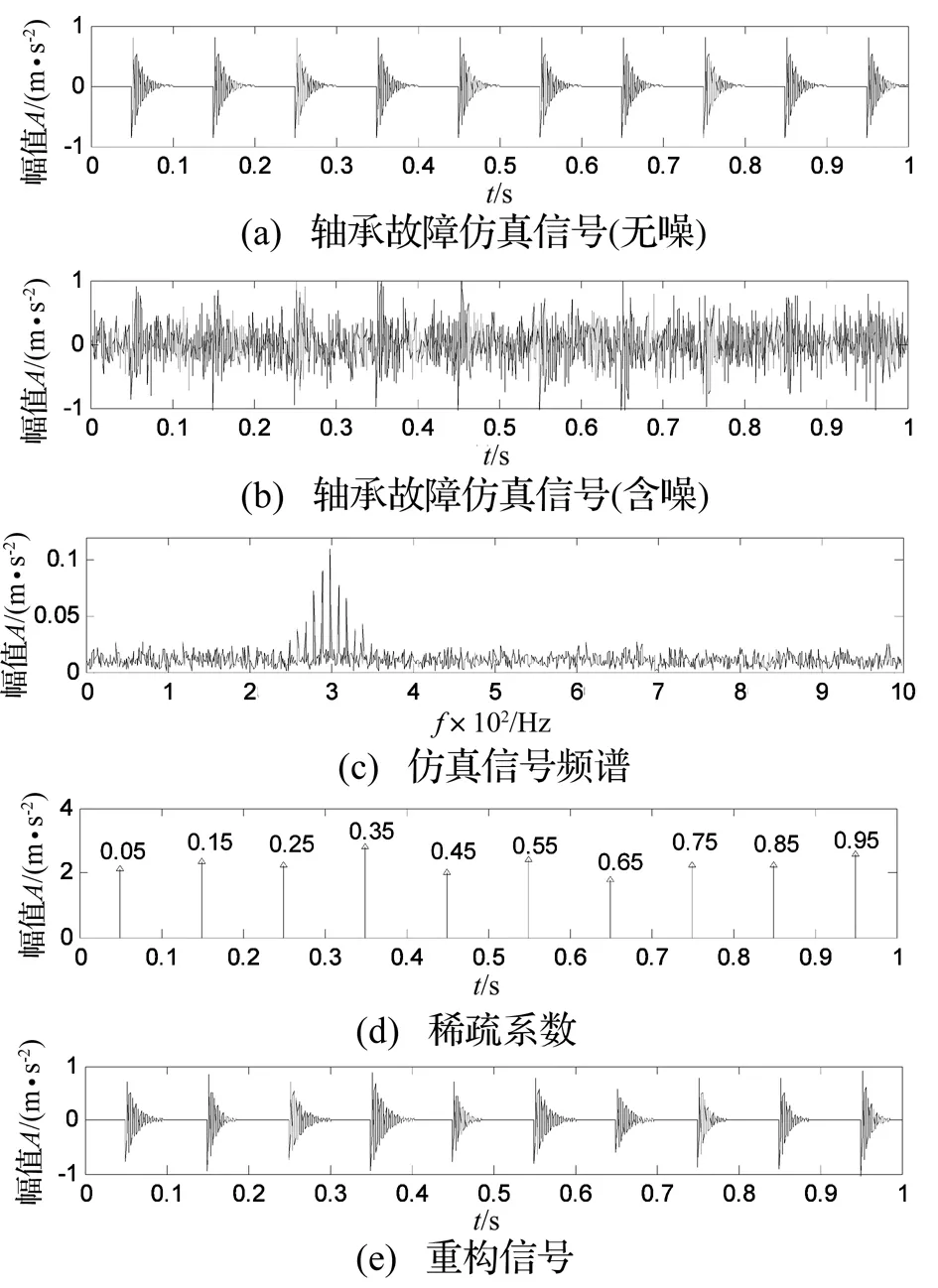
图3 轴承故障仿真信号分析结果Fig.3 Analysis results of the simulation signal

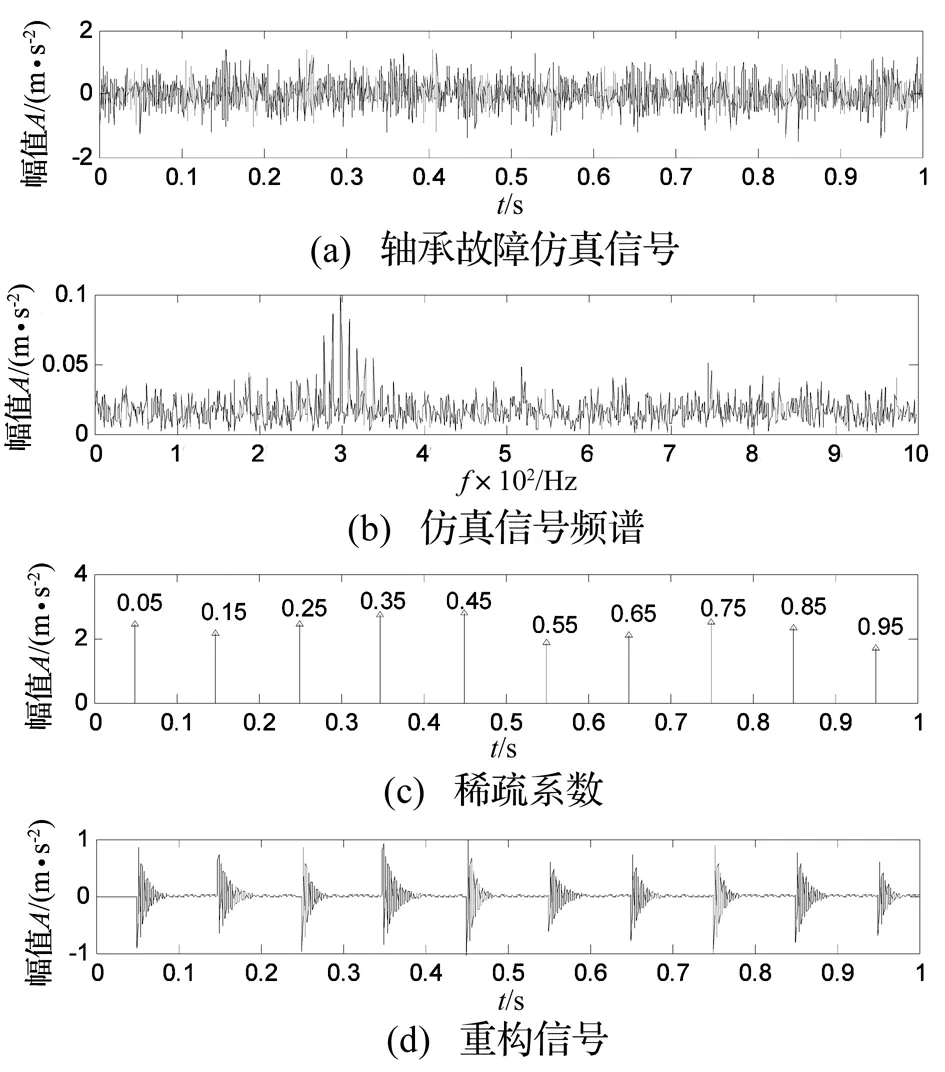
图4 轴承故障仿真信号分析结果Fig.4 Analysis results of the simulation signal

图5 基于不同算法的仿真信号分析Fig.5 Analysis of the simulation signal by using different algorithms

算法MP基本算法改进MP算法时间/min10．13240．0452

3 滚动轴承故障特征提取应用

上述仿真分析表明，由本文算法所得稀疏系数和重构信号可清楚地得到周期性特征，且具有高效，抗干扰能力强的优点。接下来将应用该方法分别对凯斯西储大学轴承数据及美国智能维护(IMS)中心轴承全寿命实验振动信号进行分析，进一步验证所提出方法的有效性。

3.1 凯斯西储大学轴承故障数据分析

实验采用6205-2RS JEM SKF深沟球轴承，实验时滚动体故障尺寸为0.18 mm，振动数据采集采样频率为48 kHz。实验时轴承转速为1 796 r/min，滚动体理论故障特征频率为119.36 Hz。

图6(a)为轴承滚动体轻微故障时的振动信号，图6(b)为该振动信号频谱，从中可以看出峰值频率为4 138 Hz。应用相关滤波法确定最佳阻尼比为0.03，按照本文方法构造Laplace小波字典，对轴承滚动体故障信号进行改进的MP快速算法进行分析，得到稀疏表示系数如图6(c)所示，从图6(c)中可以看到轴承滚动体故障冲击响应时刻，从而识别冲击时刻与故障周期，表2中给出各冲击响应时刻，并由此确定故障周期。由于实验时并不能完全保证恒速，因此采用平均周期来确定故障频率。实验测得故障频率为123.82 Hz，与滚动体理论故障频率接近，由此判断该故障为滚动体故障。对于同一信号，利用MP基本算法对故障信号进行分析，重构信号如图6(e)所示。在相同条件下，利用两种算法对故障信号进行分析，运算时间如表3所示，相较于MP基本算法，改进MP算法运算效率明显提高。

图6 轴承滚动体故障振动信号MP算法分析结果Fig.6 Analysis results for the signal of the bearing with roller fault by using MP algorithm

表3 稀疏算法运算效率比较

3.2 IMS轴承全寿命实验数据分析

为了进一步验证本文方法的有效性及对微弱故障特征提取的有效性，对IMS轴承全寿命试验不同阶段的数据进行分析。在此实验中，每隔10 min采集一次数据，采样频率为20 kHz,轴承外圈理论故障频率为236.4 Hz。图7(a)、7(b)、7(c)、7(d)分别为正常轴承、轴承外圈早期故障、中度故障及严重故障信号波形，从图中可看出，随着轴承运行时间加长，轴承故障冲击特征越来越明显。

图8(a)为轴承外圈轻微故障时的振动信号，图8(b)为该振动信号频谱，从中可以看出峰值频率为4 575 Hz。应用相关滤波法确定最佳阻尼比为0.09，按照上述原理构造Laplace小波字典，并利用本文方法对其进行稀疏表示，得到稀疏表示系数如图8(c)所示，从图8(c)中可以直观看到轴承外圈故障冲击响应时刻。从而能够有效识别冲击时刻与故障周期，表4中给出各冲击响应时刻，并由此确定故障周期。由于实验时并不能保证完全的恒速，采用平均周期来确定故障频率，为232.56 Hz，与外圈理论故障特征频率236.4 Hz接近，由此判断该故障为外圈故障，与实际一致。

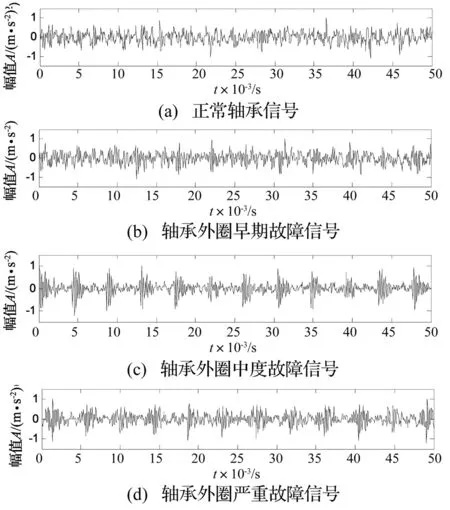
图7 不同阶段的轴承故障信号Fig.7 Bearing fault signal at different stages

时刻/ms时间间隔/ms平均周期/ms0．054．804．758．954．1512．253．3017．505．2521．854．354．3026．204．3530．554．3534．904．3539．054．1543．604．5547．353．75

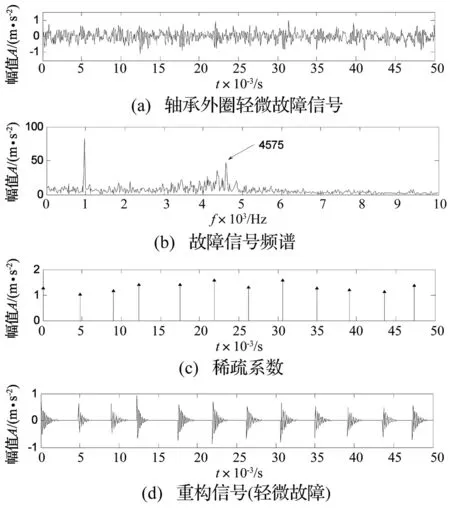
图8 轴承外圈故障MP算法分析结果Fig.8 Analysis results for the signal of the bearing with outer race fault at the early stage

4 结 论

(1)针对滚动轴承故障振动信号稀疏表示过完备字典的选择与构造问题，结合滚动轴承故障振动信号特点，基于Laplace小波原子，利用相关滤波法构造稀疏表示中的过完备字典，提高了轴承故障振动信号稀疏表示效果。

(2)针对基于匹配追踪的稀疏表示算法计算量大，效率低的问题，结合FFT快速运算的特性，通过互相关运算替换基本匹配追踪算法中的内积运算，提高算法的运算速度。

(3)实验结果表明，该方法能够较好的识别故障信号冲击响应时刻，具有较强的抑制噪声干扰的能力，同时，相较于MP基本算法，本文方法在运算效率方面有明显优势。将该方法应用于轴承故障特征提取，实验结果表明，本文方法能够有效识别轴承故障响应发生的时刻，通过分析重构信号的周期特征，判断轴承故障类型。

[ 1 ] KLEIN R, INGMAN D, BRAUN S.Non-stationary signals: phase-energy approach-theory and simulations [J]. Mechanical Systems and Signal Processing, 2001, 15(6):1061-1089.

[ 2 ] WANG S B, HUANG W, ZHU A. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis [J].Mechanical Systems and Signal Processing, 2011, 25(4):1299-1320.

[ 3 ] YAN R, GAO R X, CHEN X. Wavelets for fault diagnosis of rotary machines: A review with applications [J]. Signal Processing, 2014, 96(A):1-15.

[ 4 ] ZHU A, YAN R, LUO L, et al. Detection of signal transients based on wavelet and statistics for machine fault diagnosis[J].Mechanical Systems and Signal Processing, 2009,15(4):1076-1097.

[ 5 ] YANG Y, YU D J, CHENG J S. A roller bearing fault diagnosis method based on EMD energy entropy and ANN [J].Journal of Sound and Vibration, 2006, 294(1/2):269-277.

[ 6 ] PENG Z K, TSE P W, CHU F L. An improved Hilbert-Huang transform and its application in vibration signal analysis[J].Journal of Sound and Vibration, 2005, 286(1/2):187-205.

[ 7 ] 李昌林，孔凡让，黄伟国，等.基于EEMD和Laplace小波的滚动轴承故障诊断[J].振动与冲击, 2014, 33(3):63-69. LI Changlin, KONG Fanrang, HUANG Weiguo, et al. Rolling bearing fault diagnosis based on EEMD and Laplace wavelet [J].Journal of Vibration and Shock, 2014, 33(3):63-69.

[ 8 ] 彭畅，柏林，谢小亮.基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法 [J].振动与冲击, 2012, 31(20):143-146. PENG Chang, BO Lin, XIE Xiaoliang. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram[J].Journal of Vibration and Shock, 2012, 31(20):143-146.

[ 9 ] MALLAT S, ZHANG Z. Matching pursuits with time-frequency dictionaries [J]. IEEE Transactions on Signal Processing, 1993, 41(12):3397-3415.

[10] CUI L, WANG J, LEE S. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis [J]. Journal of Sound and Vibration, 2014, 333(10):2840-2862.

[11] 严宝康，周凤星.基于相干累积量分段正交匹配追踪方法的轴承早期故障稀疏特征提取[J]. 机械工程学报, 2014, 50(13):88-96. YAN Baokang, ZHOU Fengxing. Initial Fault identification of bearing based on coherent cumulant stage-wise orthogonal matching pursuit [J].Journal of Mechanical Engineering, 2014, 50(13):88-96.

[12] CAI G, CHEN X, HE Z.Sparsity-enabled signal decompo-sition using tunable Q-factor wavelet transform for fault feature extraction of gearbox[J]. Mechanical Systems and Signal Processing, 2013, 41(1/2):34-53.

[13] 尹忠科,邵君,VANDERGHEYNST P. 利用FFT实现基于MP的信号稀疏分解[J].电子与信息学报，2006, 25(4): 614-618． YIN Zhongke, SHAO Jun, VANDERGHEYNST P. MP based signal sparse decomposition with FFT[J].Journal of Electronics & Information Technology, 2006, 28(4):614-618.

[14] 訾艳阳，李庆祥，何正嘉. Laplace 小波相关滤波法与冲击响应提取[J].振动工程学报, 2003, 16(1):67-70. ZI Yanyang, LI Qingxiang,HE Zhengjia. Extraction of impulse response based on correlation filtering method of laplace wavelet[J]. Journal of Vibration Engineering, 2003, 16(1):67-70.

[15] 王诗彬, 朱忠奎, 王安柱.基于瞬态冲击响应参数辨识的轴承故障特征检测[J].振动工程学报, 2010, 23(4):445-449. WANG Shibin, ZHU Zhongkui, WANG Anzhu.Bearing fault feature detection based on parameter identification of transient impulse response [J].Journal of Vibration Engineering, 2010, 23(4):445-449.

Fast sparse representation algorithm based on improved MP and its applications in fault feature extraction of rolling bearings

WANG Lin, CAI Gaigai, GAO Guanqi, ZHOU Fei, YANG Siyuan, ZHU Zhongkui

(School of Urban Rail Transportation, Soochow University, Suzhou 215131, China)

At constant rotating speed, localized faults of rolling bearings in rotating machines may lead to periodic impacts and thus cause periodic transient vibration signals. The transient feature extraction always is a crucial problem for localized fault detection. The sparse decomposition based on matching pursuit (MP) is an adaptive sparse representation for signals. It is one of the effective methods for weak feature extraction. Here, aiming at the selecting and constructing problems of the over complete dictionary for sparse representation of rolling bearing fault vibration signals, the matching correlation filtering method was used to construct Laplace wavelet atoms used to match the impact waveform and construct the over-complete dictionary. Aiming at the large computational cost and low efficiency problems of the basic matching tracking algorithm, combined with FFT fast operation characteristics, the correlation algorithm was used to replace the basic matching pursuit algorithm for inner product computation to improve the computational efficiency. Simulation and test analysis results of rolling bearings with faults showed that the proposed algorithm can extract their fault features accurately and efficiently.

rolling bearing; matching pursuit; dictionary construction; Fast Fourier Transform(FFT); feature extraction

国家自然科学基金(51405321);江苏省自然科学基金(BK20140339);江苏省高校自然科学基金(14KJB460023);江苏省大学生创新训练(201410285103X);苏州市应用基础研究(SYG201511)

2015-09-14 修改稿收到日期：2016-01-13

王林 男，硕士生，1993年生

蔡改改 女，博士,副教授，1986年生

TH165；TN911

A

10.13465/j.cnki.jvs.2017.03.028