颗粒调谐质量阻尼器减震控制的数值模拟

鲁 正， 陈筱一， 王佃超， 吕西林

(1.同济大学 土木工程防灾国家重点实验室，上海 200092； 2.同济大学 结构工程与防灾研究所，上海 200092)

颗粒调谐质量阻尼器减震控制的数值模拟

鲁 正1,2， 陈筱一2， 王佃超2， 吕西林1,2

(1.同济大学 土木工程防灾国家重点实验室，上海 200092； 2.同济大学 结构工程与防灾研究所，上海 200092)

提出一种颗粒调谐质量阻尼器，即通过摆绳将颗粒阻尼器悬挂于主体结构上，将目前广泛应用的调谐质量阻尼器与减震效能优越的颗粒阻尼器结合起来，以扩大减振频带，增加减振鲁棒性。基于一定的等效原则将多颗粒阻尼器等效为单颗粒阻尼器，提出一种近似的颗粒调谐质量阻尼器数值模拟方法，并介绍了系统参数的取值方法。进行了附加颗粒调谐质量阻尼器的单自由度结构实际地震输入下的振动台试验，通过对比试验结果与数值模拟结果，发现两者吻合较好，说明该简化方法可以较好地模拟颗粒调谐质量阻尼器的减震控制效果。

颗粒调谐质量阻尼器；调谐质量阻尼器；颗粒阻尼器；数值模拟；结构振动控制

调谐质量阻尼器(Tuned Mass Damper,TMD)由质量块、弹簧和阻尼系统组成，通过调整TMD的自振频率，使其接近主体结构的被控频率，当主体结构受迫振动时，TMD随之产生与主体结构相反的运动并施加反作用力于主体结构，输入结构的振动能量通过调谐质量阻尼器逐步消散，从而控制结构的振动[1]。近年来，通过颗粒-结构、颗粒-颗粒之间的非弹性碰撞与摩擦来实现动量交换及结构能量耗散的颗粒阻尼器，克服了调谐质量阻尼器减振频带窄的缺点，具有对原系统改动小、可靠度高、耐久性好、对温度变化不敏感(在颗粒金属熔点以下均可正常使用，钨粉能承受近2 000 ℃高温)、易于用在恶劣环境等优点[2]，受到了广大土木工程研究人员的重视，但目前在实际建筑结构工程中的应用甚少。本文尝试将目前已成熟应用于工程实际的TMD与颗粒阻尼技术结合起来，通过摆绳将填充颗粒群的容器悬挂于主体结构上，形成一种新型的颗粒调谐质量阻尼器，以增强其在地震激励下的能量耗散，并扩大其减振频带。

对于颗粒阻尼器在地震、风振等荷载下颗粒行为的数值模拟始终是一个难点。考虑到多颗粒碰撞引起运动量的突变，使其动力学行为表现出很强的非线性，系统很难得到解析解，学者们研究出一些简化方法和数值方法。PAPALOU等[3]将多颗粒阻尼器通过一定的等效原则简化为单颗粒阻尼器；FRIEND等[4]提出一种解析方法，即把多颗粒模拟为一个凝聚的质量块，并将各种机理引起的能量耗散由一个通过实验拟合得到的“有效恢复系数”表示；鲁正等[5]基于离散单元法，建立了颗粒阻尼器对多自由度结构进行减震控制的数值模拟方法；闫维明等[6]建立了调谐型颗粒阻尼器的数值分析简化模型，并提出了该模型等效阻尼比的能量估算方法。此外，学者们还提出了回归模型法[7]和恢复力曲面法[8]等应用于颗粒阻尼技术的数值模拟方法。

本文提出一种新型的颗粒调谐质量阻尼器，基于等效前后颗粒阻尼器中腔体空隙体积相等以及颗粒质量相等的原则，将多颗粒阻尼器等效为单颗粒阻尼器，建立颗粒调谐质量阻尼器的数值模型，并进行试验验证，为今后工程应用提供一种简单高效的分析方法。

1 数值模拟方法

本节采用等效的简化方法来分析颗粒调谐质量阻尼器的减震效果。颗粒调谐质量阻尼器将颗粒阻尼器腔体通过摆绳与主体结构相连，对于腔体可按照单摆进行简化，在传统颗粒阻尼器的基础上增加一个自由度即可。以下重点讨论对多颗粒阻尼器的简化方法。

1.1 多颗粒阻尼器等效方法

由于多颗粒在碰撞时表现出很强的非线性，因此要进行带有多颗粒阻尼器的动力系统的精确分析是相当困难的。鉴于单颗粒阻尼器的理论分析比较完善，并考虑阻尼器的运动特点，本节采用以单颗粒阻尼器等效替代多颗粒阻尼器的方法来研究其振动响应[3]。等效原则如下：

(1)等效前后阻尼器腔体中的空隙体积相等。

(2)等效前多颗粒总质量与等效后单颗粒质量相等。

(3)等效前后颗粒均为球形，且密度均为ρ。

(4)等效前的多颗粒阻尼器为长方体，等效后的单颗粒阻尼器为圆柱体，且圆柱体的直径与等效后单颗粒的直径相等。

依据以上原则等效后得到的单颗粒阻尼器示意图，如图1所示。等效前后颗粒调谐质量阻尼器的参数及符号见表1。

图1 多颗粒阻尼器和等效的单颗粒阻尼器Fig.1 Diagrams of particle damper and equivalent single unit impact damper

类型物理意义符号表示多颗粒阻尼器腔体尺寸(长，宽，高)(dx，dy，dz)单个颗粒质量m1p颗粒总质量m颗粒直径Dp单颗粒阻尼器颗粒质量m3颗粒直径D颗粒自由运动距离d

简化方法如下：

等效前颗粒在阻尼器中占据的体积Vspd由式(1)得出，式中N是颗粒的总数，即N=m/m1p：

(1)

多颗粒阻尼器中的空隙体积Vepd由式(2)得出，式中Vpd是颗粒阻尼器的体积，并假设盒子颗粒与腔体的体积比，即颗粒填充率ρp=Vspd/Vpd：

Vepd=Vpd-Vspd=(1/ρp-1)Vspd

(2)

等效后单颗粒阻尼器的空隙体积Veid为：

(3)

根据等效原则式(1)，令式(2)和式(3)相等，可得：

(4)

HALES[9]的研究表明，半径相等的球在发生球密堆积时体积比不能超过0.74，即ρp≤0.74。根据等效原则式(2)，m=m3，至此，建立了等效的单颗粒阻尼器中颗粒自由运动长度的表达式，即式(4)。

1.2 颗粒调谐质量阻尼器系统控制方程

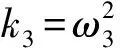
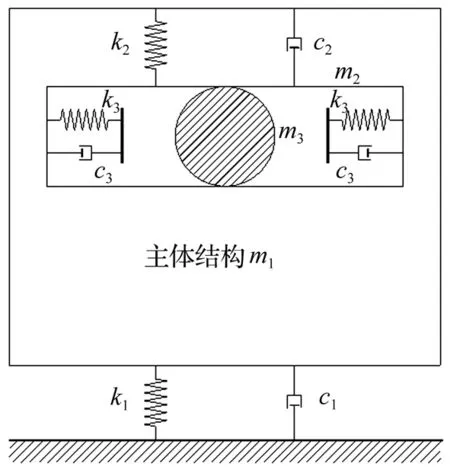
图2 计算模型简图Fig.2 Schematic diagram of computational models

其系统的控制方程用矩阵表示为

[K]{X(t)}={Fp(t)}

(5)

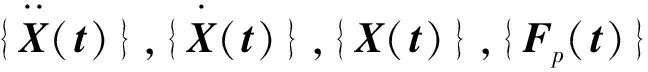
设振动台的位移为xg(t)，主体结构的位移为x1(t)，质量为m1；腔体的位移为x2(t)，质量为m2；颗粒的位移为x3(t)，质量为m3。则系统控制方程展开如

图3 G(y)和的形式Fig.

1.3 数值模拟流程

本文对于颗粒调谐质量阻尼器的数值模拟采用如下的流程：①确定主体结构、颗粒调谐质量阻尼器和荷载的相关参数，并确定结构的初始运动状态；②计算等效的单颗粒阻尼器的自由运动距离d；③计算主体结构动力响应，绘制数值模拟结果的响应时程曲线并与实际测量曲线对比，并对比响应的峰值结果。参数选取详见2.2。

该数值模拟过程运用MATLAB软件实现，调用程序中内置的求常微分方程数值解的方法ode45，即四阶-五阶龙格-库塔(Runge-Kutta)算法。输入主体结构和颗粒调谐质量阻尼器的相关参数，以及1.2中的控制方程，即可进行迭代求解。

2 数值模拟结果及试验验证

为了验证本文提出的简化方法用于颗粒调谐质量阻尼器减震控制模拟的可行性和合理性，开展了一个单自由度结构附加颗粒调谐质量阻尼器的模拟地震振动台试验。

1.4 试验简介

试验主体结构模型为单自由度钢排架，为了模拟常见的高层结构，调整结构的基频至1.0 Hz左右，在结构顶部附加6 kg质量块，最终其自振频率为1.37 Hz。填充颗粒的盒子通过四根细线垂直悬吊在结构顶部。盒子横截面尺寸相同，均为60 mm×60 mm，长度为80 mm。盒子内置26颗直径为10 mm的钢球，颗粒密度为ρ=7 644 kg/m3，单个颗粒质量为m1p=0.032 kg。

试验中采用El-Centro波和Kobe波作为结构底部的振动输入。在进行数值模拟时，从采集的台面加速度时程曲线中截取一个完整波作为计算输入波。为方便起见，将各质点的位移和速度初值赋为0。本文将计算得到的结构顶层加速度与位移时程曲线与试验采集得到的结果进行比较，通过二者的对比来验证该简化方法的准确性。关于试验过程及结果在文献[10]中有详细介绍，本文仅介绍数值模拟参数的选取和结果。

2.2 数值模拟参数取值

主体结构的质量可以通过测量模型的实际质量得到，其圆频率和阻尼比可以通过试验前的白噪声扫频，并考虑模型加工误差，采用半功率法得到。同理，可得阻尼器腔体的质量，考虑到调谐的因素，其圆频率与主体结构的自振圆频率取值相同。

腔体的阻尼比较难测得，在数值模拟时通过试算的方式确定，计算发现当腔体阻尼比低于0.05时，主体结构的响应几乎不变，即主体结构的响应对于腔体阻尼比并不敏感。本文取腔体阻尼比为ξ2=0.05。

根据MASRI[11]的研究，当ω3≥20ω1时，可以较合适地模拟颗粒与容器壁的相互作用。本文取颗粒圆频率ω3=20ω1，即ω3=172.16 rad/s。

颗粒的阻尼比ξ3与颗粒的恢复系数e存在如图4所示的关系[5]。在本文的试验中，根据文献[12]，颗粒的恢复系数e一般取为0.25，由图4关系可得ξ3=0.375。

数值模拟中用到的系统参数汇,总如表2所示。

由于振动台面的数据采集频率为500 Hz，因此上述数值模拟过程均以0.002 s为计算步长。

图4 颗粒阻尼比与恢复系数关系图Fig.4 Relationship between damping ratio ξ3 and coefficient of restitution e

Tab.2 Values of system parameters

质量/kg圆频率/(rad·s-1)阻尼比主体结构7．68．6080．032阻尼器腔体0．1288．6080．05等效后的单颗粒0．832172．160．375

2.3 数值模拟结果

图5显示了附加颗粒调谐质量阻尼器的单层钢排架模型顶层在El-Centro波地震激励下加速度和位移响

应的计算值和试验值对比曲线。总体上看，两者符合较好，但有部分区段计算值和试验值存在一定误差。一方面是由于为方便起见，数值模拟时将位移和速度初值赋为零所致，随着计算的逐步进行，初值的选取对结构在地震激励下响应的影响逐渐减小；另一方面是由于颗粒阻尼器在地震激励下表现出很强的非线性，本文提出的数值模拟方法对此有一定程度的简化，比如并未考虑颗粒之间的碰撞的影响。

此外，表3列出了附加不同颗粒形式的颗粒调谐质量阻尼器的结构模型在不同激励下的顶层峰值和均方根加速度响应计算值与试验值的对比，发现峰值加速度两者吻合较好，而均方根加速度也可以将误差控制在可接受的范围内。事实上，在高层建筑结构抗震设计的时候，对于主体结构舒适度的要求，主要就反映在最大加速度的数值上面，设计人员对该数值十分关心。而本简化方法能对该数值给出一定程度的合理预测。

图5 附加颗粒调谐质量阻尼器模型顶层在地震激励(El-Centro波)下的响应Fig.5 Response at roof level of the test frame with particle tuned mass damper under earthquake excitations (El-Centro Wave)

地震波类型颗粒形式峰值加速度计算值/(m·s-2)试验值/(m·s-2)误差/%均方根加速度计算值/(m·s-2)试验值/(m·s-2)误差/%4个20mm钢球2．60242．56451．460．56960．53785．58El⁃Centro5个20mm钢球2．60492．6949-3．460．55820．55380．7919个10mm钢球1．96741．92991．900．57710．54944．8126个10mm钢球1．88331．82593．050．57630．56072．714个20mm钢球3．52153．5518-0．860．50560．5377-6．34Kobe5个20mm钢球3．74003．73540．120．53450．5799-8．4919个10mm钢球3．88693．85620．790．52450．5751-9．6426个10mm钢球3．64103．7484-2．950．49830．5435-9．07

总体而言，本文提出的数值模拟方法能够较合理地计算出附加颗粒调谐质量阻尼器系统在实际地震激励下的响应，并且由于其原理简单、操作方便，具有一定的实用价值。然而，要更精确的模拟附加颗粒调谐质量阻尼系统在地震激励下的行为，尤其是考虑颗粒之间碰撞对减振性能的影响，还需要进一步的研究。

3 结 论

本文在颗粒阻尼器和调谐质量阻尼器的基础上，结合各自的优点，提出一种新型的颗粒调谐质量阻尼器。基于等效前后颗粒阻尼器内空隙与腔体体积比一致以及多颗粒总质量与等效后单颗粒质量相等的原则，将多颗粒阻尼器简化为单颗粒阻尼器，建立颗粒调谐质量阻尼器的数值模型，并介绍了系统参数的取值方法。为了验证该方法的可行性和准确性，进行了附加颗粒调谐质量阻尼器的单自由度结构实际地震输入下的振动台试验，通过数值模拟结果与试验结果的对比发现两者整体吻合较好，并且加速度峰值和均方根也吻合良好，说明该简化方法可以较好地模拟颗粒调谐质量阻尼器的减震控制效果，有助于进一步了解其物理本质，从而为进一步推广其在土木工程中的应用提供有效的分析途径。

[ 1 ] 李晓玮,施卫星. 人行天桥MTMD减振控制的鲁棒性研究[J]. 结构工程师,2012，28(4)：7-12. LI Xiaowei，SHI Weixing. Research on robustness of vibration control of pedestrian bridges using multi degree of freedom passive tuned mass-dampers [J].Structure Engineers, 2012，28(4)：7-12.

[ 2 ] 鲁正,吕西林,闫维明. 颗粒阻尼技术研究综述[J]. 振动与冲击,2013,32(7):1-7. LU Zheng，LÜ Xilin，YAN Weiming. A survey of particle damper technology [J]. Journal of Vibration and Shock, 2013, 32(7):1-7.

[ 3 ] PAPALOU A，MASRI S F. Performance of particle dampers under random excitation [J].Journal of Vibration and Acoustics,1996，118(4):614-621.

[ 4 ] FRIEND R D，KINRA V K. Particle impacting damping [J]. Journal of Sound and Vibration,2000,233(1):93-118.

[ 5 ] 鲁正,吕西林. 颗粒阻尼器减震控制的数值模拟[J]. 同济大学学报(自然科学版),2013, 41(8):1140-1144. LU Zheng，LÜ Xilin. Numerical simulation of vibration control effects of particle dampers [J]. Journal of Tongji University (Natural Science),2013,41(8):1140-1144.

[ 6 ] 闫维明,许维炳,王瑾,等. 调谐型颗粒阻尼器简化力学模型及其参数计算方法研究与减震桥梁试验[J]. 工程力学,2014,31(6):79-84. YAN Weiming，XU Weibing，WANG Jin，et al. Experimental and theoretical research on the simplified mechanical model of a tuned particle damper，its parameter determination method and earthquake-induced vibration control of bridge [J]. Engineering Mechanics,2014, 31(6):79-84.

[ 7 ] 胡溧,黄其柏,许智生. 颗粒阻尼的回归分析研究[J]. 中国机械工程,2008,19(23):2834-2837. HU Li,HUANG Qibai,XU Zhisheng. Regression analysis of particle damping [J]. China Mechanical Engineering,2008, 19(23):2834-2837.

[ 8 ] 蒋华,陈前. 恢复力曲面法在颗粒阻尼器研究中的应用[J]. 振动、测试与诊断,2007,27(3):228-231. JIANG Hua,CHEN Qian. Application of restoring force surface method in particle damping research [J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27(3):228-231.

[ 9 ] HALES T C. The sphere packing problem [J]. Journal of Computational and Applied Mathematics,1992，164(1): 53-65.

[10] 施卫星,何斌,李晓玮,等. 一种新型调谐质量阻尼器的试验研究[J]. 振动与冲击, 2015,34(12):207-211. SHI Weixing，HE Bin，LI Xiaowei，et a. Experimental study on a new type of tuned mass damper [J]. Journal of Vibration and Shock, 2015, 34(12):207-211.

[11] MASRI S F,IBRAHIM A M. Response of the impact damper to stationary random excitation [J]. The Journal of the Acoustical Society of America, 1973, 53(1):200-211.

[12] 葛藤,贾智宏,周克栋. 钢球和刚性平面弹塑性正碰撞恢复系数研究[J]. 工程力学,2008,25(6):209-213. GE Teng,JIA Zhihong,ZHOU Kedong. Research on elastoplastic normal impact of steel spheres against a rigid plane [J]. Engineering Mechanics, 2008, 25(6):209-213.

Numerical simulation for vibration reduction control of particle tuned mass dampers

LU Zheng1,2, CHEN Xiaoyi2, WANG Dianchao2, LÜ Xilin1,2

(1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;2.Research Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China)

A particle tuned mass damper was proposed by hanging a particle damper on a main structure through a string. It combines a widely used tuned mass damper with an efficient particle damper in vibration control area. Thus it is able to increase the robustness of damping performance within a wider frequency band. Here, an approximate numerical simulation method for particle tuned mass dampers was proposed based on an equivalent priciple to take a multi-particle damper as an equivalents single-particle damper. The method to determine the corresponding system parameters was also introduced. A series of shaking table tests of a single DOF structure attached with a particle tuned mass damper under seismic imputs were performed. A comparative study showed that the simulation results agree well with the test ones, so the proposed simplified method can be used to simulate vibration reduction control effects of particle tuned mass dampers.Key words: particle tuned mass damper; tuned mass damper; particle damper; numerical simulation; structural vibration control

国家自然科学基金(51478361);中央高校基本科研业务费专项资金项目

2015-11-20 修改稿收到日期：2016-01-24

鲁正 男，博士，副教授，1982年生

TU352；TB535

A

10.13465/j.cnki.jvs.2017.03.008