混合效应模型中的方差成分检验*

曾 平 赵 杨 陈 峰

混合效应模型中的方差成分检验*

曾 平1赵 杨2陈 峰2

在很多科学问题中需要在混合效应模型框架下对随机效应方差成分(暂记为τ2)进行假设检验[1-6]，也即检验H0:τ2=0。除直接科学兴趣外，许多间接医学问题也能转化为对方差成分的检验。例如，为判断在惩罚样条回归中是参数模型还是非参数模型更合适，Claeskens[7]首先建立混合效应模型，将模型选择问题转化为对随机效应方差成分是否等于零的假设检验问题，最后通过限制性似然比检验H0:τ2=0。其他研究者也用同样的方法处理过类似问题[8-12]。然而，方差成分为非负参数，对方差成分的假设检验是非标准的：在H0下τ2位于参数空间边缘。由于这种限制，常用的渐近χ2无效分布对似然比统计量不再成立[1-3,8]。混合效应模型中的方差成分检验吸引了广泛研究兴趣[7-8，13-19]。本文主要介绍方差成分检验的似然比方法，方差成分得分检验或Wald检验可参考其他相关文献[13,20,21]。

线性混合效应模型的方差成分检验

设Y为连续变量，X=(X1,…,Xp)和Z=(Z1,…,Zq)分别为n×p和n×q的矩阵，n为样本量。在广泛意义上Y、X和Z既适于非独立数据结构[22-25]，如重复测量数据或聚群数据[26-29]，也适于独立数据情形[7-11,30,31]，如惩罚样条回归。更加详细的例子可参考上述文献。Y、X和Z之间的关系由线性混合效应模型[25]刻画

(1)

用矩阵的形式模型(1)可表达为

Y=Xβ+Zb+ε,b～N(0,τ2K),ε～N(0,σ2In)

(2)

式中β为固定效应，b为随机效应，τ2为未知方差成分，K为已知q×q矩阵描述随机效应间相互关系，In为n维单位阵，σ2为残差方差，与b不相关。模型中Y的期望和方差分别为

E(Y)=Xβ,Var(Y)=τ2ZKZ′+σ2In=σ2Vλ

(3)

其中Vλ=λZKZ′+In,λ=τ2/σ2。设参数为θ=(β,λ,σ2)，模型(2)的对数似然函数为

(4)

似然比统计量定义为

LRTn=2sup[H1(θ)-H0(θ)]

(5)

1.渐近混合卡方分布

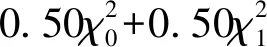
2.基于谱分解的模拟分布

为了获得似然比统计量的无效分布，Crainiceanu

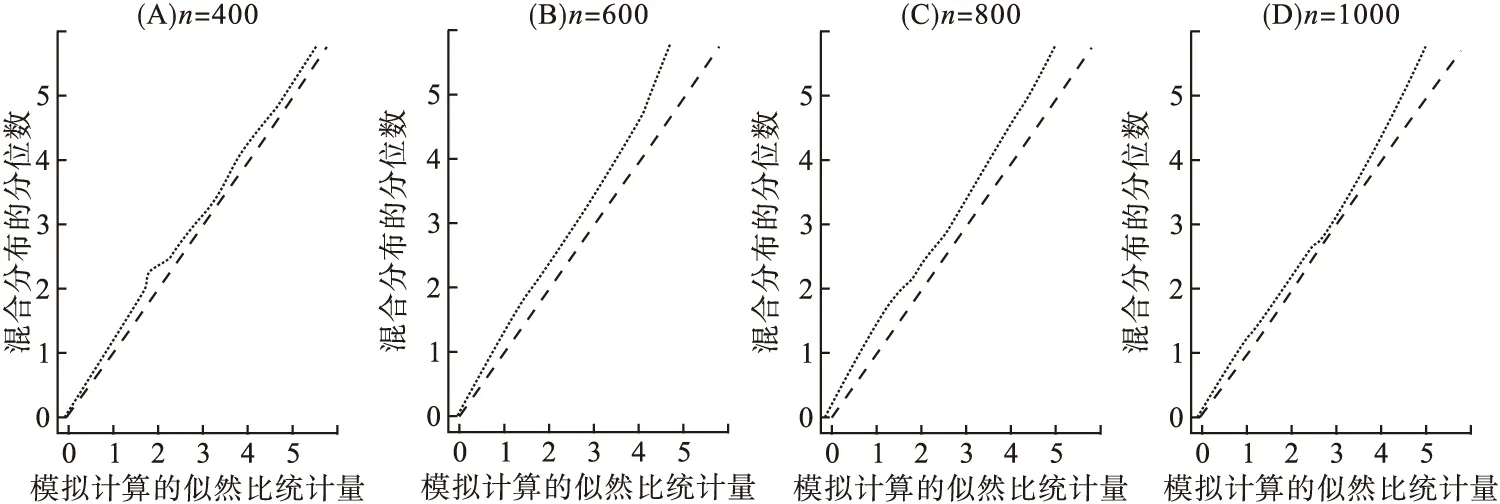
图1 模拟计算的似然比统计量和的分位数。

和Ruppert在谱分解基础上提出了一种基于模拟抽样算法[8]。假设模型(2)中λ已知，可获得β和σ2的极大似然估计值

(6)

带入对数似然函数，获得剖面似然函数

(7)

定义

(8)

ξ是矩阵K1/2Z′ZK1/2的特征根，其中，

(9)

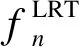
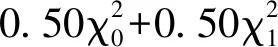
3.重抽样方法

统计分析中当面对复杂假设检验时诉诸于重抽样方法是一种常用策略[34-39]。重抽样避免了数学推导，概念上简单并且容易操作，属于计算密集型统计技术。Fitzmaurice等[14]以及Lee和Braun[40]提出了似然比方差成分的permutation检验，Faraway[23]建立了似然比方差成分的参数bootstrap检验。其他研究者对似然比方差成分提出了类似的重抽样检验方法[15-16]。

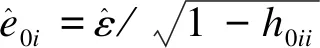
广义线性混合效应模型的方差成分检验

1.logistic混合效应模型和PQL算法

目前几乎所有似然比方差成分检验都是在线性混合效应模型框架下完成，即都是针对连续应变量的；而对离散应变量似然比方差成分检验的研究还很少。以logistic回归为例，接下来讨论广义混合效应模型的似然比方差成分检验。设Y为二分类应变量，X和Z同前。Y、X和Z之间的关系通过logistic混合效应模型[22,41-42]描述

(10)

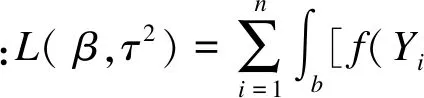
2[Lτ2≥0(β,τ2)-L(β,τ2=0)]

(11)

然而，由于对数似然函数涉及积分运算，实际中除极有限和简单情况外，大多数时候都无法精确计算Lτ2≥0(β,τ2)和获得精确的对数似然值。因此不能直接通过式(11)进行似然比检验。

logistic混合模型的参数估计算法包括数值积分[43]，惩罚拟似然(penalized quasi-likelihood，PQL)和边际拟似然(marginal quasi-likelihood，MQL)[42]，伪似然估计[41]，Monte Carlo估计[44-45]和Gibbs抽样[46]。数值积分只适用于低维度的积分运算，一般很难处理超过五维的积分[22]；Monte Carlo估计和Gibbs抽样的不足在于计算繁重。PQL和MQL能够通过近似方法有效处理高维积分问题，计算相对简单，且能够通过重复调用已有的线性混合模型程序执行。对logistic混合模型进行方差成分的似然比检验至少包含以下的三个困难[47]：与线性混合模型不同，通常不能获得关于logistic混合模型对数函数的闭型表达式，因此精确计算logistic混合模型的对数似然值和似然比统计量变得很困难；由于涉及高维计算运算，很难获得logistic混合模型参数的精确估计值；即使能够有效估计logistic混合模型和计算其对数似然比统计量，如何获得该统计量的无效分布也不清楚。基于logistic混合模型已有的理论发展，本文仅仅专注其方差成分的似然比检验。

2.基于重抽样方法的伪似然比方差成分检验

为了处理上面的问题，可以通过基于重抽样的伪似然比方法进行方差成分检验[47]。具体步骤如下：①采用PQL算法估计logistic混合模型参数；PQL算法可通过R软件中的函数glmmPQL进行，该函数包含在MASS软件包中[48]；②当PQL算法收敛时，有工作应变量

(12)

和伪似然函数

(13)

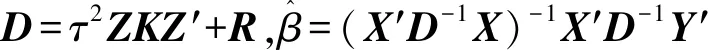
其他问题和可能的研究方向

目前，由于以下几方面的原因，似然比方差成分检验主要集中在线性混合效应模型并且模型中只包含一个方差成分[8,12,17-18]：①能够较为容易估计线性混合效应模型的参数和计算其对数似然值，进而计算似然比统计量；②多个方差成分共存时，不存在简单的对数似然函数谱分解形式，因此很难获得似然比统计量的无效分布；③由于可能的高维积分运算，一般难以精确估计广义混合效应模型的参数和计算其对数似然值，以及获得似然比统计量的无效分布；④重抽样方法属于计算密集型统计方法，难以大规模运用。

在标准的参数假设检验中似然比检验被证明是在小样本时最优的[49]。事实上，由于似然比检验充分利用了H0条件下的模型和H1条件下的模型，相对得分检验和Wald检验，似然比检验被证明在非标准参数假设检验也具有更高统计效能[7,30,50]。因此，推广和发展似然比检验以适合更加广泛的情形具有理论和实际意义。具体而言，以下几方面问题值得进一步探索：①在线性混合效应模型中当存在多个方差成分而仅对其中某个成分感兴趣时，Greven[12]等建议可以首先从应变量中消除冗余随机效应；此时，尚包括应变量的残差和待检验方差成分，然后按照前文只包含单个方差成分的似然比检验进行统计分析。然而，这样做的缺点在于，没有考虑到随机效应之间可能存在的相关，而且在模型估计多个方差成分时还可能存在数值问题，如模型不收敛或计算不稳定。②在线性混合效应模型中假设残差是独立的；当存在相关协方差结构，即ε～N(0,R(α))，R为一般形式协方差矩阵、包含未知参数向量α；在这种情况下可先估计残差协方差，在此基础上建立伪数据，然后将伪数据当做原始数据按照线性混合效应模型框架下相似的方法进行似然比方差成分检验[18]。但这种方法在协方差矩阵R的选择以及其适用性等方面需要更多的研究。③前文在广义线性混合效应模型框架下建立的伪似然比方差成分检验其有效性取决于PQL算法；PQL算法本身属于有偏估计；虽然提出了校正PQL偏倚的算法[51-55]，有偏和无偏的参数估计算法对伪似然比方差成分检验的影响如何还需进一步研究[47]。④当前讨论的方差成分检验都假设被检验的方差成分和其他冗余成分之间独立，如何在考虑方差成分相关的前提下建立有效的似然比检验？⑤如何进一步在广义线性混合效应模型框架下发展在计算上更加有效的似然比检验、而不仅仅依赖于重抽样方法？⑥虽然似然比检验具有更高的统计效能，但是由于其需要同时估计H0条件下的模型和H1条件下的模型，所以相对得分检验，计算速度明显较慢；因此，需要发展有效的计算方法提高似然比检验的计算速度，以适合大规模的应用[8,12]。

[1]Self SG,Liang KY.Asymptotic Properties of Maximum Likelihood Estimators and Likelihood Ratio Tests under Nonstandard Conditions.J R Stat Soc B,1987,82(398):605-610.

[2]Stram DO,Lee JW.Variance Components Testing in the Longitudinal Mixed Effects Model.Biometrics,1994,50(4):1171-1177.

[3]Liang KY,Self SG.On the Asymptotic Behaviour of the Pseudolikelihood Ratio Test Statistic.J R Stat Soc B,1996,58(4):785-796.

[4]Lindquist MA,Spicer J,Asllani I,et al.Estimating and testing variance components in a multi-level GLM.Neuroimage,2012,59(1):490-501.

[5]Drikvandi R,Verbeke G,Khodadadi A,et al.Testing multiple variance components in linear mixed-effects models.Biostatistics,2013,14(1):144-159.

[6]Nobre J,Singer J,Sen P.U-tests for variance components in linear mixed models.Test,2013,22(4):580-605.

[7]Claeskens G.Restricted likelihood ratio lack-of-fit tests using mixed spline models.J R Stat Soc B,2004,66(4):909-926.

[8]Crainiceanu CM,Ruppert D.Likelihood ratio tests in linear mixed models with one variance component.J R Stat Soc B,2004,66(1):165-185.

[9]Crainiceanu CM,Ruppert D.Restricted likelihood ratio tests in nonparametric longitudinal models.Stat Sinica,2004,14(3):713-730.

[10]Crainiceanu CM,Ruppert D.Likelihood ratio tests for goodness-of-fit of a nonlinear regression model.J Multivariate Anal,2004,91(1):35-52.

[11]Crainiceanu C,Ruppert D,Claeskens G,et al.Exact likelihood ratio tests for penalised splines.Biometrika,2005,92(1):91-103.

[12]Greven S,Crainiceanu CM,Küchenhoff H,et al.Restricted Likelihood Ratio Testing for Zero Variance Components in Linear Mixed Models.J Comput Graph Stat,2008,17(4):870-891.

[13]Lin X.Variance component testing in generalised linear models with random effects.Biometrika,1997,84(2):309-326.

[14]Fitzmaurice GM,Lipsitz SR,Ibrahim JG.A Note on Permutation Tests for Variance Components in Multilevel Generalized Linear Mixed Models.Biometrics,2007,63(3):942-946.

[15]Sinha SK.Bootstrap tests for variance components in generalized linear mixed models.Scand J Stat,2009,37(2):219-234.

[16]Samuh MH,Grilli L,Rampichini C,et al.The Use of Permutation Tests for Variance Components in Linear Mixed Models.Commun Stat Theor M,2012,41(16-17):3020-3029.

[17]Staicu A-M,Li Y,Crainiceanu CM,et al.Likelihood ratio tests for dependent data with applications to longitudinal and functional data analysis.Scand J Stat,2014,41(4):932-949.

[18]Wiencierz A,Greven S,Küchenhoff H.Restricted likelihood ratio testing in linear mixed models with general error covariance structure.Electron J Stat,2011,5:1718-1734.

[19]Chen Y,Liang KY.On the asymptotic behaviour of the pseudolikelihood ratio test statistic with boundary problems.Biometrika,2010,97(3):603-620.

[20]Lin X,Zhang D.Inference in generalized additive mixed models by using smoothing splines.J Roy Stat Soc,B,1999,61(2):381-400.

[21]Zhang D,Lin X.Hypothesis testing in semiparametric additive mixed models.Biostatistics,2003,4(1):57-74.

[22]Diggle P,Heagerty P,Liang KY,et al.Analysis of longitudinal data,2nd Edition.New York:Oxford University Press,2002.

[23]Faraway JJ.Extending the linear model with R:generalized linear,mixed effects and nonparametric regression models.New York:Chapman & Hall,2005.

[24]Pinheiro JC,Bates D.Mixed-Effects Models in S and S-PLUS,2nd Edition.New York:Springer,2009.

[25]Laird NM,Ware JH.Random-effects models for longitudinal data.Biometrics,1982,38(4):963-974.

[26]张岩波,何大卫,刘桂芬,等.重复测量数据的混合模型及其MIXED过程实现-混合线性模型及其SAS软件实现.中国卫生统计,2001,18(5):272-275.

[27]杨珉.多元分析的发展-多水平模型简介.中国卫生统计,1994,11(5):32-35.

[28]曾平,曹红艳,刘桂芬.重复测量计数资料的随机效应ZIP模型.中国卫生统计,2009,26(4):344-346,349.

[29]任仕泉,陈峰.多水平统计模型在多中心临床试验评价中的应用.中国卫生统计,2000,17(2):108-110.

[30]Zeng P,Zhao Y,Liu J,et al.Likelihood Ratio Tests in Rare Variant Detection for Continuous Phenotypes.Ann Hum Genet,2014,78(5):320-332.

[31]Wu MC,Lee S,Cai T,et al.Rare-Variant Association Testing for Sequencing Data with the Sequence Kernel Association Test.Am J Hum Genet,2011,89(1):82-93.

[32]Lehmann EL,Romano JP.Testing statistical hypotheses,3rd Edition.New York:Springer,2006.

[33]Scheipl F,Greven S,Küchenhoff H.Size and power of tests for a zero random effect variance or polynomial regression in additive and linear mixed models.Comput Stat Data Anal,2008,52(7):3283-3299.

[34]Davison AC,Hinkley DV.Bootstrap Methods and Their Application.Cambridge:Cambridge University Press,1997.

[35]Efron B,Tibshirani R.An Introduction to the Bootstrap.New York:Chapman and Hall,1993.

[36]Good P.Permutation,Parametric,and Bootstrap Tests of Hypotheses,3rd Edition:New York:Springer,2005.

[37]荀鹏程,赵杨,易洪刚,等.Permutation Test 在假设检验中的应用.数理统计与管理,2006,25(5):616-621.

[38]陈峰,陆守曾,杨珉.Bootstrap 估计及其应用.中国卫生统计,1997,14(5):5-7.

[39]刘沛,刘元宝,王灿楠.膳食暴露评估模型及其构建方法.中华预防医学杂志,2007,41(6):502-504.

[40]Lee OE,Braun TM.Permutation Tests for Random Effects in Linear Mixed Models.Biometrics,2012,68(2):486-493.

[41]Wolfinger R,O′.Connell M.Generalized linear mixed models a pseudo-likelihood approach.J Stat Comput Sim,1993,48(3-4):233-243.

[42]Breslow NE,Clayton DG.Approximate Inference in Generalized Linear Mixed Models.J Am Stat Assoc,1993,88(421):9-25.

[43]曹红艳,刘桂芬,曾平,等.预测性伪似然法和贝叶斯法广义线性混合模型估计.中国药物与临床,2008,8(11):861-863.

[44]McCulloch CE.Maximum Likelihood Variance Components Estimation for Binary Data.J Am Stat Assoc,1994,89(425):330-335.

[45]McCulloch CE.Maximum likelihood algorithms for generalized linear mixed models.J Am Stat Assoc,1997,92(437):162-170.

[46]Zeger SL,Karim MR.Generalized linear models with random effects:a Gibbs sampling approach.J Am Stat Assoc,1991,86(413):79-86.

[47]Zeng P,Zhao Y,Chen F.Permutation-based variance component test in generalized linear mixed model with application to multilocus genetic association study.BMC Med Res Methodol,2015,15:37.

[48]Venables WN,Ripley BD.Modern Applied Statistics with S,4th Edition.New York:Springer,2002.

[49]Donoho D,Jin J.Higher criticism for detecting sparse heterogeneous mixtures.Ann Stat,2004,32(3):962-994.

[50]Zeng P,Zhao Y,Zhang L,et al.Rare Variants Detection with Kernel Machine Learning Based on Likelihood Ratio Test.PLoS ONE,2014,9(3):e93355.

[51]Lin X,Breslow NE.Bias Correction in Generalized Linear Mixed Models with Multiple Components of Dispersion.J Am Stat Assoc,1996,91(435):1007-1016.

[52]Wang N,Lin X,Gutierrez RG,et al.Bias Analysis and SIMEX Approach in Generalized Linear Mixed Measurement Error Models.J Am Stat Assoc,1998,93(441):249-261.

[53]Pawitan Y.Two-staged estimation of variance components in generalized linear mixed models.J Stat Comput Sim,2001,69(1):1-17.

[54]Breslow NE,Lin X.Bias correction in generalised linear mixed models with a single component of dispersion.Biometrika,1995,82(1):81-91.

[55]Jiang J.Consistent Estimators in Generalized Linear Mixed Models.J Am Stat Assoc,1998,93(442):720-729.

(责任编辑：邓 妍)

*：国家自然科学基金项目(81402765，81473070，81373102)；国家统计局全国统计科学研究项目(2014LY112)；江苏省教育厅高校哲学社会科学研究基金项目(2013SJD790032，2013SJB790059)；南京医科大学公共卫生学院优秀博士论文培育项目

1. 徐州医科大学公共卫生学院流行病与卫生统计学教研室(221004)

2. 南京医科大学公共卫生学院生物统计学系