样本量估计及其在nQuery+nTerim和SAS软件上的实现
——均数比较(八)*
2017-03-09南方医科大学公共卫生学院生物统计学系詹志颖曹颖姝段重阳陈平雁
南方医科大学公共卫生学院生物统计学系 詹志颖 曹颖姝 段重阳 陈平雁
样本量估计及其在nQuery+nTerim和SAS软件上的实现
——均数比较(八)*
南方医科大学公共卫生学院生物统计学系 詹志颖 曹颖姝 段重阳 陈平雁△
1.2.1.9 两组泊松分布均数比较

1.非限制性最大似然估计(MLE,简记W1)
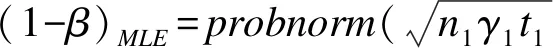
(1-34)
2.限制性最大似然估计(CMLE,简记W2)
(1-35)
3.对数转换的非限制性最大似然估计(ln(MLE),简记W3)
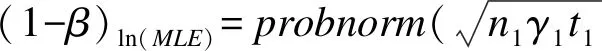
(1-36)
4.对数转换的限制性最大似然估计(ln(CMLE),简记W4)

(1-37)
5.方差稳健估计(VS,简记W5)

(1-38)
式中,n1与n2、γ1与γ2以及t1与t2分别为试验组与对照组的样本量、单位时间内事件发生率以及个体平均观察时间;c=R0/R1,其中R0和R1分别为零假设和备择假设下两组发生率的比值;ρ=R0t2n2/t1n1。
在计算样本量时,一般先设定样本量初始值,然后迭代样本量直到所得的检验效能满足条件。此时的样本量,即研究所需的最小样本量。
【例1-25】某研究欲探索使用荷尔蒙人群(试验组)与未使用荷尔蒙人群(对照组)单位时间内冠心病发病率是否相同。要求试验组与对照组样本量比例为2:1,观察时间为2年。根据以往研究,试验组冠心病发病率为0.0005,对照组发病率是试验组的4倍。设定检验水准为0.05,试估计当检验效能为90%时所需的样本量[8]。
nQuery+nTerim 4.0实现:设定检验水准α=0.05,检验效能1-β=90%。原假设为试验组与对照组发病率相同,即总体R0=1;备择假设为对照组发病率是试验组的4倍,即总体R1=4。
在nQuery+nTerim 4.0主菜单选择:
Goal:⊙Means
Number of Groups:⊙Two
Analysis Method:⊙Test
方法框中选择:Two Poisson Means
在弹出的样本量估计窗口,将各参数值键入,选择统计量,结果如图1-61所示,即W1(MLE):试验组需要8564人,对照组需要4282人,总样本量为12846人;W2(CMLE):试验组需要6889人,对照组需要3445人,总样本量为10334人;W3(ln(MLE))和W4(ln(CMLE)):试验组需要6685人,对照组需要3343人,总样本量为10028人;W5(VS)):试验组需要8590人,对照组需要4295人,总样本量为12885人。W1与W5方法估计的样本量偏大,其余三种方法相对来说较接近且偏少。
SAS程序:
OPTIONS LINESIZE=MAX;proc IML;
start PSMS(a,R0,R1,stat,t1,t2,rate1,nr,power);
/*a 检验水准;R0、R1分别为H0、H1下两组发生率比值;stat检验统计量(1:W1,2:W2,3:W3,4:W4,5:W5);t1、t2分别为试验组、对照组个体平均观察时间;rate1试验组发生率;nr=n2/n1;power检验效能*/
error=0;if(a>1|a<0)|(R0<0)|(R1<0)|(stat^=1 & stat^=2 & stat^=3 & stat^=4 & stat^=5)|
(t1<0)|(t2<0)|(rate1<0)|(nr<0)|(power>100|power< 1) then error=1;
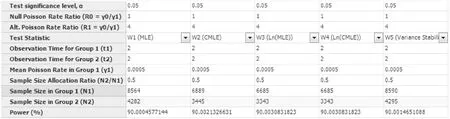
图1-61 nQuery+nTerim 4.0关于例1-25样本量估计的参数设置与计算结果
if(error=1) then stop;if(error=0) then do;n1=1;rou=R0*t2*nr/t1;c=R0/R1;
do until(pwer>=power/100);n1=n1+1;n2=ceil(n1*nr);if(stat=1) then do;ts=“W1”;
pwer=probnorm((sqrt(n1*rate1*t1)*abs(1-c))/sqrt(c/rou+c**2)-probit(1-a));end;
else if(stat=2) then do;ts=“W2”;pwer=probnorm((sqrt(n1*rate1*t1)*abs(1-c))/sqrt(c/rou+c**2)-probit(1-a)*sqrt((c+rou)/(1+c*rou)));end;else if(stat=3) then do;ts=“W3”;pwer=probnorm(sqrt(n1*rate1*t1)*abs(log(c))/sqrt(c/rou+1)-probit(1-a));end;
else if(stat=4) then do;ts=“W4”;pwer=probnorm(sqrt(n1*rate1*t1)*abs(log(c))/sqrt(c/rou+1)-probit(1-a)*(sqrt(c*(rou**2+2*rou+1))/(c+rou)));end;else do;ts=“W5”;pwer=probnorm((2*abs(1-sqrt(c))*sqrt(n1*rate1*t1+3/8)-probit(1-a)*sqrt(c/rou+c))/sqrt(c/rou+1));end;end;pwer=round(pwer*100,0.000000000001);print a R0 R1 ts t1 t2 rate1 n1 n2 nr pwer[label=“power(%)”];end;finish PSMS;
run PSMS(0.05,1,4,1,2,2,0.0005,0.5,90);
run PSMS(0.05,1,4,2,2,2,0.0005,0.5,90);
run PSMS(0.05,1,4,3,2,2,0.0005,0.5,90);
run PSMS(0.05,1,4,4,2,2,0.0005,0.5,90);
run PSMS(0.05,1,4,5,2,2,0.0005,0.5,90);quit;
SAS运行结果见图1-62。
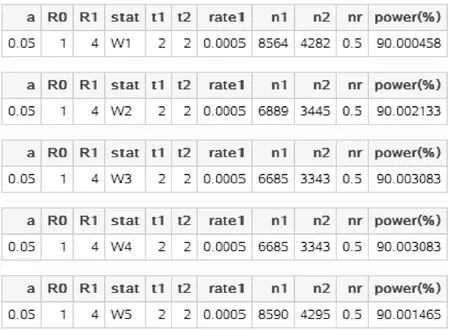
图1-62 SAS 9.4关于例1-25样本量 估计的参数设置与计算结果
1.2.1.10 两组负二项分布均数比较
方法:Zhu和Lakkis(2014)[9]提出的两组负二项分布均数差异性检验的样本量估计方法是建立在均值为ln(r1/r2),方差为σ2=(1/n2)[(1/μt)[1/r2+1/(θr1)]+(1+θ)k/θ]的正态分布基础上,其检验效能的计算公式为:
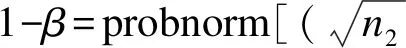
(1-39)
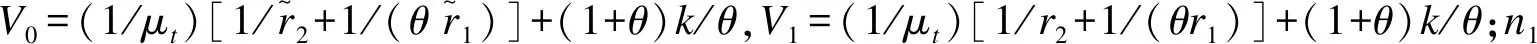
(1)Reference Rate(RR):
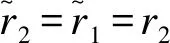
V0(RR)=(1+θ)/(θμtr2)+(1+θ)k/θ
(1-40)
(2)True Rates(TR):
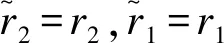
V0(TR)=(1/μt)[1/r2+1/(θr1)]+(1+θ)k/θ
(1-41)
(3)Maximum Likelihood(ML)

V0(ML)=(1+θ)2/[θμt(r2+θr1)]+(1+θ)k/θ
(1-42)
在计算样本量时,一般先设定样本量初始值,然后迭代样本量直到所得的检验效能满足条件。此时的样本量,即研究所需的最小样本量。
【例1-26】慢性阻塞性肺病的恶化事件研究中,对照组事件率为0.8人年,试验组较对照组有15%的减少(r1/r2=0.85),平均暴露时间为0.75年,离散参数为0.7,且为均衡设计(θ=1)。设定检验水准为0.05,试估计当检验效能为80%时研究所需样本量[9]。
nQuery+nTerim 4.0实现:
设定检验水准α=0.05,检验效能1-β=80%。原假设为试验人群与对照人群的事件率相同,即总体r1=r2;备择假设为对照人群事件率与试验人群不同,即总体r1≠r2。
在nQuery+nTerim 4.0主菜单选择:
Goal:⊙Means
Number of Groups:⊙Two
Analysis Method:⊙Test
方法框中选择:Two Negative Binomial Rates
在弹出的样本量估计窗口,将各参数值键入,结果如图3-63所示,即Reference Rate方法,两组各需1433人,总样本量为2866人;True Rates方法,两组各需1494人,总样本量为2988人;Maximum Likelihood方法,两组各需1490人,总样本量为2980人。
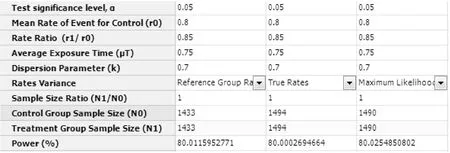
图1-63 nQuery+nTerim 4.0关于例1-26样本量估计的参数设置与计算结果
SAS程序:
OPTIONS LINESIZE=MAX;proc IML;
start NBR(a,r2,rr,miut,k,rv,nr,power);
/*a 检验水准; r2 对照组平均事件率;rr=r1/r2;miut个体平均暴露时间;k 离散参数;rv方差(V0)的计算方法;1:RR;2:TR;3:ML;nr=n1/n2,n1与n2分别为试验组与对照组的样本量;power 检验效能*/
error=0;if(a>1|a<0)|(r2<0)|(rr<0)|(miut<0)|(k<0)|(rv^=1 &rv^=2 &rv^=3)|(nr<0)|(power>100|power< 1) then error=1;if(error=1) then stop;if(error=0) then do;n2=2;r1=r2*rr;
v1=(1/r2+1/(nr*r1))/miut+(1+nr)*k/nr;if(rv=1) then do;rvlbl=“RR”;
v0=(1+nr)/(nr*miut*r2)+(1+nr)*k/nr;end;else if(rv=2) then do;rvlbl=“TR”;
v0=(1/r2+1/(nr*r1))/miut+(1+nr)*k/nr ;end;else do;rvlbl=“ML”;
v0=(1+nr)**2/(nr*miut*(r2+nr*r1))+(1+nr)*k/nr ;end;do until(pwer>=power);n2=n2+1;pwer=100*probnorm((sqrt(n2)*abs(log(rr))-probit(1-a/2)*sqrt(v0))/sqrt(v1));end;n1=nr*n2;pwer=round(pwer,0.0000001);print a r2 rr miut k rvlbl[lable=“rv”] n1 n2 nr pwer[label=“power(%)”];end;finish NBR;
run NBR(0.05,0.8,0.85,0.75,0.7,1,1,80);
run NBR(0.05,0.8,0.85,0.75,0.7,2,1,80);
run NBR(0.05,0.8,0.85,0.75,0.7,3,1,80);
quit;
SAS运行结果:
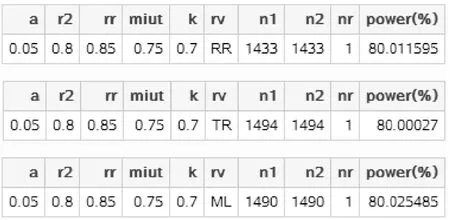
图1-64 SAS 9.4关于例1-26样本量估计的 参数设置与计算结果
[1]吕朵,段重阳,陈平雁.样本量估计及其在nQuery和SAS软件上的实现—均数比较(一),中国卫生统计,2012,29(1):127-131.
[2]邓居敏,吕朵,陈平雁.样本量估计及其在nQuery和SAS软件上的实现—均数比较(二),中国卫生统计,2012,29(1):132-134.
[3]段重阳,吕朵,陈平雁.样本量估计及其在nQuery和SAS软件上的实现—均数比较(三),中国卫生统计,2012,29(2):275-278.
[4]段重阳,吕朵,陈平雁.样本量估计及其在nQuery和SAS软件上的实现—均数比较(四),中国卫生统计,2012,29(2):279-283.
[5]吕朵,段重阳,陈平雁.样本量估计及其在nQuery和SAS软件上的实现—均数比较(五),中国卫生统计,2012,29(3):451-455.
[6]段重阳,吕朵,陈平雁.样本量估计及其在nQuery和SAS软件上的实现—均数比较(六),中国卫生统计,2012,29(3):456-459.
[7]张斌,吕朵,陈平雁等.样本量估计及其在nQuery和SAS软件上的实现—均数比较(七),中国卫生统计,2012,29(4):598-602.
[8]Gu K,Ng HKT,Tang ML,et al.Testing the ratio of two poisson rates.Biometrical Journal,2008,50(2):283-298.
[9]Zhu H,Lakkis H.Sample size calculation for comparing two negative binomial rates.Statistics in medicine,2014,33(3):376-387.
(责任编辑:郭海强)
*本研究得到国家自然科学基金资助(编号:81673270)

编者按:本文为南方医科大学陈平雁教授团队2012年发表于本刊的《样本量估计及其在nQuery+nTerim和SAS软件上的实现—均数比较》系列文章[1-7]的后续部分。前期主要考虑了连续变量和等级变量的情形,本文将介绍离散变量,即两组泊松分布及负二项分布均数比较的样本量估计方法。文中的公式和实例序号均依照前期的系列文章顺序编排,以保持原有结构。
△通信作者:陈平雁
