重复测量诊断试验的ROC曲线广义线性混合效应模型*
2017-03-09马春桃田茂再
马春桃 熊 巍 田茂再,3,4
·论著·
重复测量诊断试验的ROC曲线广义线性混合效应模型*
马春桃1熊 巍2田茂再1,3,4
目的 针对重复测量诊断数据,为同时考虑协变量对诊断试验准确性评价的影响,度量重复测量数据间的相关性,本文探索新的ROC曲线的建模方法。方法 通过广义线性混合效应模型对ROC曲线进行模拟,并采用贝叶斯参数估计方法,利用WinBUGS软件予以实现,进而计算不同协变量取值下的ROC曲线下面积(AUC)以对诊断试验结果进行评价。结果 实例数据分析结果表明,基于广义线性混合效应模型的ROC曲线建模方法可以有效地刻画重复测量诊断试验数据,给出更有解释意义的回归参数,提供临床分析的参考依据。结论 基于广义线性混合效应的ROC曲线模型在解决重复测量诊断试验的准确度评价问题起着至关重要的作用。
ROC曲线 混合效应 贝叶斯 重复测量 诊断试验
在医学诊断等领域中,为了准确评价某一诊断方法的准确度,试验常以重复测量的方式进行[1]。重复测量诊断试验是指一个患者接受多个试验或者某试验被同一患者重复接受多次的情况。同一患者的重复测量值之间是非独立的,后一次的诊断试验结果可能受到前面试验结果的影响,诊断试验结果在所测量的时间范围内可能成趋势性变化,不同患者之间的试验结果一般是独立的[2]。为正确区分人群健康状态、及时干预病人疾病进程和治疗,重复测量诊断试验的准确性是研究的关键。为此,应综合考虑混合效应模型和ROC曲线分析方法度量重复测量诊断数据间的相关关系。
ROC曲线(receiver operating characteristic curves)方法已广泛应用于临床诊疗医学领域,是描述和比较诊断试验的一种重要的综合评价方法。目前,有关诊断试验准确性最常用的指标为灵敏度和特异度,ROC曲线通过构图能够反映不同临界点下灵敏度和特异度的关系,并可通过计算ROC曲线下面积(AUC)判断诊断试验的效率。但是常规的ROC分析方法不能用来处理重复测量诊断数据,在实际问题研究中存在些许缺陷:或是建立的随机效应模型不包含协变量,无法考虑多种混杂因素(协变量)对诊断试验准确度的影响;或是建立的模型为ROC曲线的间接模型,难以给出回归参数的合理性解释。例如一类常用的间接模型就是先计算协变量组合的准确度指标(如AUC),再建立协变量对该指标影响的线性回归模型。而该类间接模型,其分析对象主要为ROC曲线的某种综合指标(如AUC),无法直接讨论协变量的影响;并且协变量不含有“疾病状态”这个重要的指示变量;与此同时该模型只能模拟协变量为分类变量的情形,这也要求协变量组合中有足够的患者数据来计算准确度指标。
混合效应模型不仅可以分析重复测量数据,还能处理诸如含有缺失数据或不均衡数据的资料。混合效应模型既考虑了固定效应也考虑了随机效应,能够有效刻画数据不独立的情况,使得信息利用更加充分;另外该模型不仅能够用于说明变量水平及变化趋势,也适用于分析协变量存在的情况。广义线性混合效应模型是广义线性模型和混合效应模型的推广,对响应变量是离散变量和分类变量的情形均适用,并通过在模型中加入随机效应项来刻画数据内部的相关性、异质性及过离散等问题。因此,广义线性混合效应模型非常适用于处理重复测量诊断试验数据。
为有效解决以上难题,本文给出适合重复诊断测量试验的ROC模型,考虑利用广义线性混合效应模型对ROC曲线进行模拟。该方法与传统方法相比,具有一定优势:一方面该方法直接对ROC曲线建模,不仅给出更有解释意义的回归参数,还考虑了协变量和随机效应的多重影响;另一方面该模型适用广泛,对离散和连续的协变量均适用,对诊断试验结果的分布也没有特定要求。这为医学诊断试验评价的ROC曲线分析提供了新的思路,为临床试验提供一定依据。
原理与方法
1.ROC曲线广义线性混合效应模型
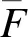
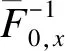
通过广义线性混合效应模型,已知基准函数向量h(p)和协变量值x,建立随机效应回归模型:
ROCx(p)=g[γ′h(p)+β′x+λ′z]
其中,g(·)是已知的连接函数,且g(·)必须是严格单调上升或下降的函数,这样才能确保ROC曲线在(0,1)区间内是单调递增的;h(p)是定义ROC曲线的形状和位置的已知的基准函数向量;γ是假阳性率FPRs影响相应真阳性率TPRs的未知参数向量;β是协变量对ROC曲线影响的回归参数向量;λ为随机效应向量,且假定λ~N(0,D)。一般地,连接函数选取probit连接函数,即g=Φ(·),基准函数向量h(p)=[1,Φ-1(p)]′,Φ(·)指累积标准正态分布函数,Φ-1(·)指累积标准正态分布函数的逆函数。
ROC曲线下面积(AUC)是评价诊断试验最常用的一个指标,它表示诊断系统中“患病”(阳性)和“不患病”(阴性)诊断结果分布与“金标准”的重叠程度,体现了诊断试验的价值,面积越大诊断价值越高。理论上AUC的取值范围为0.5~1,两端点分别表示完全无价值的诊断及完善的诊断。一般ROC曲线面积在0.50~0.70,表示诊断准确度低,在0.70~0.90,表示诊断准确度中等,0.90以上,认为诊断准确度较高。
2.参数估计方法
本文采用马尔科夫蒙特卡洛(Markov chain Monte Carlo,MCMC)的贝叶斯方法来估计ROC曲线广义线性混合效应模型。相比于极大似然估计方法,该方法更加灵活准确,且用于估计的随机效应变量个数可以是任意的。本文用WinBUGS软件来进行计算。具体的参数估计过程如下[3-5]:
第一步,给定假阳性率集,Γ=(p)
基于Alonzo和Pepe(2001)的模拟研究,可选择50个等间距的FPRs,即Γ=(1/51,…,50/51),不仅可以保证模型参数估计的有效性和稳健性,还能节约模型估计的运算时间,实现用较小的假阳性率集获得较大假阳性率集的统计功效。
第二步,确定参数γ,β,D的先验分布
(γ|A)~U(-A,A)
(β|B)~U(-B,B)
(D-1|V,v)~Wishart(V-1,v)
第三步,MCMC过程
为获得γ,β,D的后验分布,此处采用Gibbs抽样方法,迭代更新方法如下,对于第k步,k=1,…,n,直至收敛:
(1)(γ|λ(k),p,y)
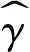
(2)(β|λ(k),y)
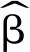
(3)(D|λ(k))
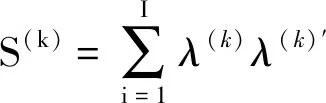
(4)(λ|γ(k),β(k),D(k),y)
通过数值迭代产生λ(k+1)。
第四步,绘制ROC曲线并计算曲线下面积AUC
根据模型参数的贝叶斯估计结果,可以绘制不同协变量组合下的ROC曲线,并计算其AUC,评价诊断试验的准确度。
实例分析
某研究组为探讨在考虑体质指数(BMI)、每天的饮酒量等影响因素后,谷丙转氨酶ALT(U/L)对肝胆病的诊断价值,在某医院收集了52名疑似肝炎患者的资料。经临床诊断,患者31例,非患者21例,并对他们进行了10次重复测量。数据资料的下载地址为:http://archive.ics.uci.edu/ml/datasets.html。本研究收集分析的部分数据见表1和表2。表3 给出了几个重要特征变量的分布。
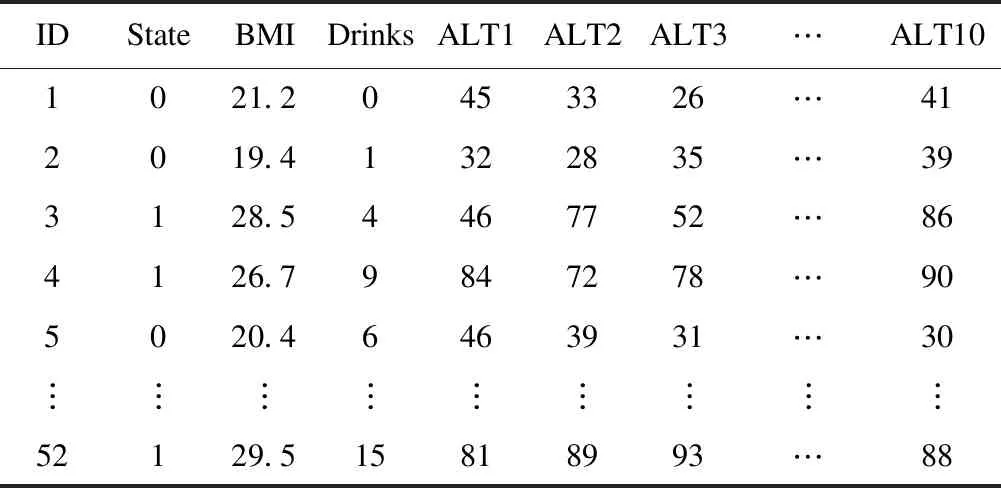
表1 52名疑似肝炎患者的资料

表2 变量描述
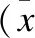
表3 各指标的统计描述±s)
表3表明,患者与非患者的体质指数、酗酒量、谷丙转氨酶的测量值是显著不同的,经检验证实,患者与非患者之间各指标的差别均有统计学意义。患者的体质指数、酗酒量、谷丙转氨酶的测量值均高于非患者。对本实例,我们考虑几种不同的情形深入分析。
1.不考虑协变量和数据间的相关性对肝炎诊断准确性的影响。由R软件绘制得到相应的ROC曲线见图1,计算AUC为0.75,可以认为谷丙转氨酶对肝炎的诊断的准确度尚可。
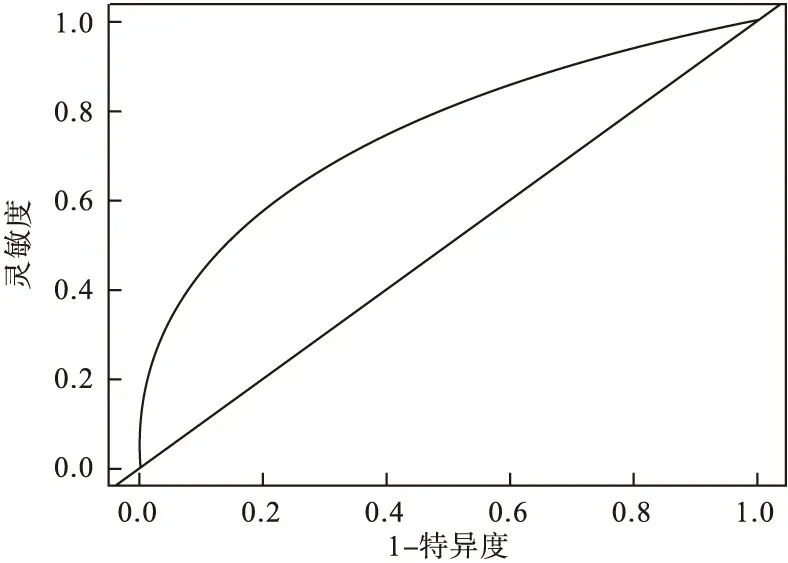
图1 未考虑协变量和随机效应影响的ROC曲线
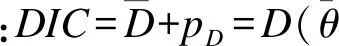
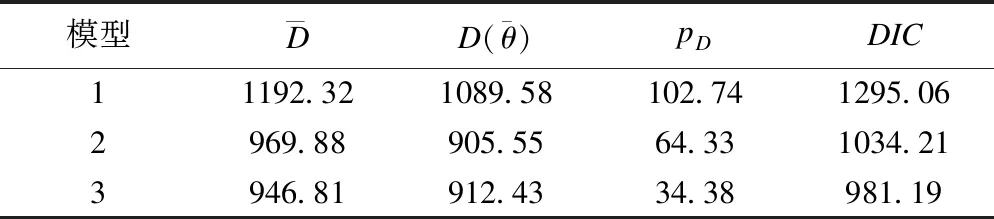
表4 三种模型DIC及相关数值比较
表4列出了如上三个模型的DIC值,可以看出模型3的DIC值最小,所以选择带截距、时间项随机效应的ROC曲线回归模型进行下一步分析,即
ROCx(p)=Φ(γ1+γ2Φ-1(p)+β1x1+β2x2+λ0+λ1t)
该模型可以在WinBUGS软件中用贝叶斯图建模的方法表示成如图2所示的有向关系图。
观察模拟结果迭代过程的踪迹和自相关函数图(如图3、图4),各参数的迭代轨迹趋于一条近似平稳的水平线,滞后一次的自相关函数趋于0,这表明模拟结果的迭代过程基本收敛,得到的贝叶斯参数估计结果(表5)可以用于下一步的统计推断。图5的核密度函数图给我们一些启示,随机效应方差的核密度函数基本呈偏态分布,所以参数估计结果取中位数更好。故我们取中位数作为各参数的估计结果。

图2 带截距、时间项随机效应的ROC曲线 混合效应模型有向图
由表5可知,Φ-1(p) 和各参数的后验均数的 95%的置信区间都没有包含0,表明各协变量对 ALT
诊断肝胆疾病准确度的影响均有统计学意义。不同患者间的随机效应方差为0.101,可以认为不同患者的ALT对肝胆疾病诊断试验的准确度不同,存在“个体效应”。不同患者时间的随机效应方差也有统计学意义,方差为0.149,可以认为不同患者的ALT对肝胆疾病的诊断准确度存在着随时间而变化的趋势。估计方程结果显示,在考虑了“个体效应”后,体质指数BMI值越小,每天的饮酒量越多,谷丙转氨酶对肝胆疾病的诊断准确性越高,也就是说,当采用谷丙转氨酶诊断肝胆疾病时,区分非肥胖患者的准确度高于肥胖患者的准确度,区分酗酒患者的准确度高于不酗酒患者的准确度。
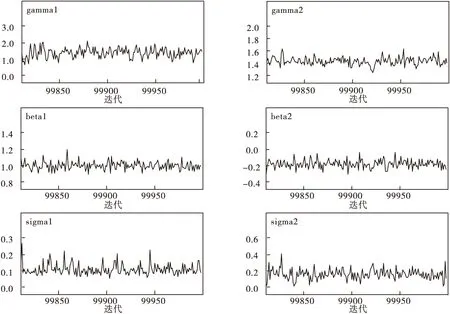
图3 迭代10万次各参数迭代轨迹
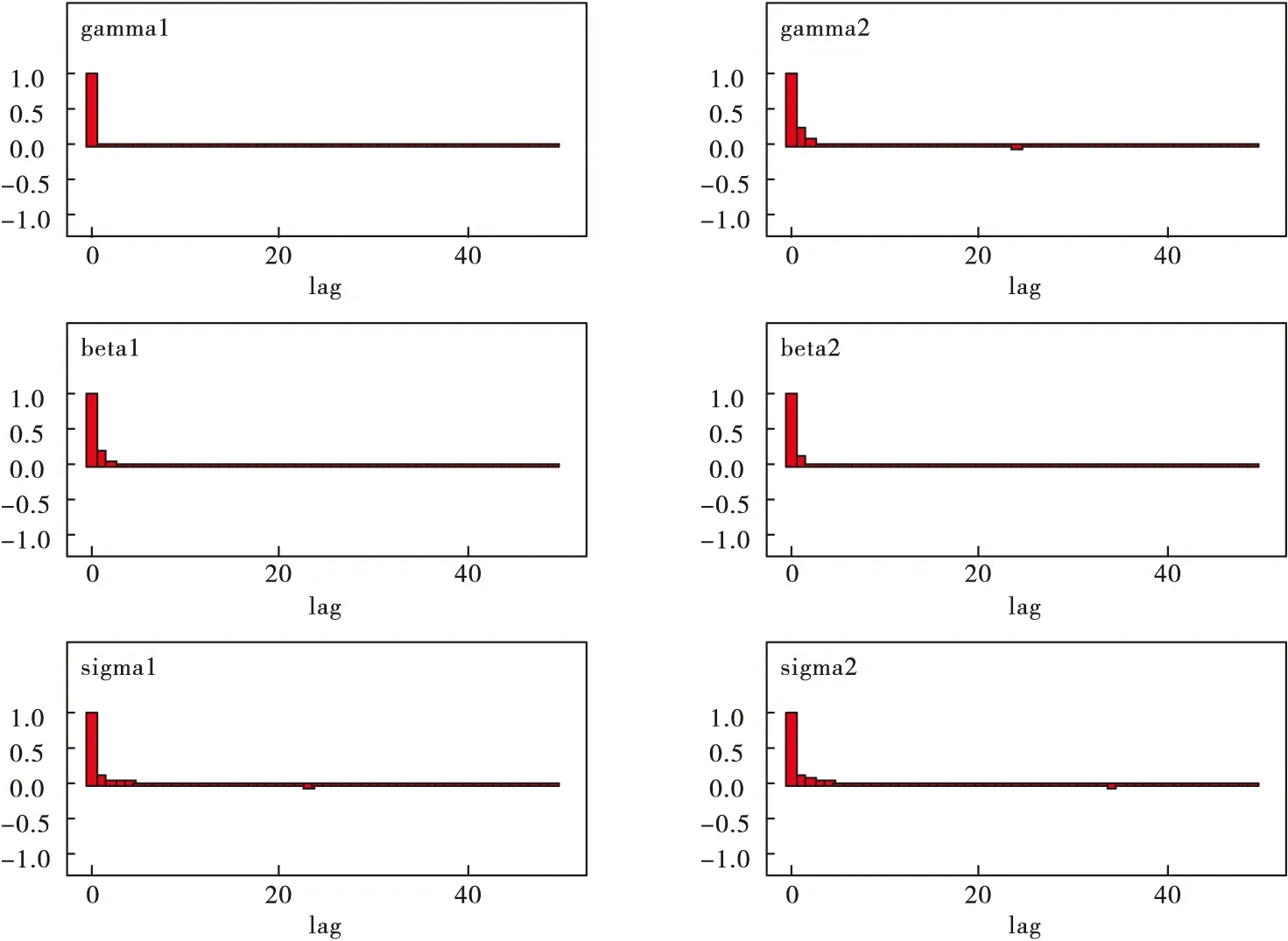
图4 各参数迭代10万次自相关函数图
根据分层拟合的模型,可以得到不同肥胖程度不同酗酒量下,谷丙转氨酶诊断肝胆疾病的ROC曲线。分别选取BMI值为23,26,29,酗酒量为0,5,10,20,计算相应的AUC,见表6。
由表6可知,不同肥胖程度,不同酗酒量下的AUC不同。若不考虑协变量和随机效应对ROC曲线的影响,有可能导致ALT对于肥胖患者或者不嗜酒的患者的预测肝胆疾病的准确性下降,给临床疾病的确诊和干预治疗提供不良的诊断信息。所以基于广义线性随机效应的ROC曲线模型可以有效地对重复测量试验诊断数据进行刻画和分析。
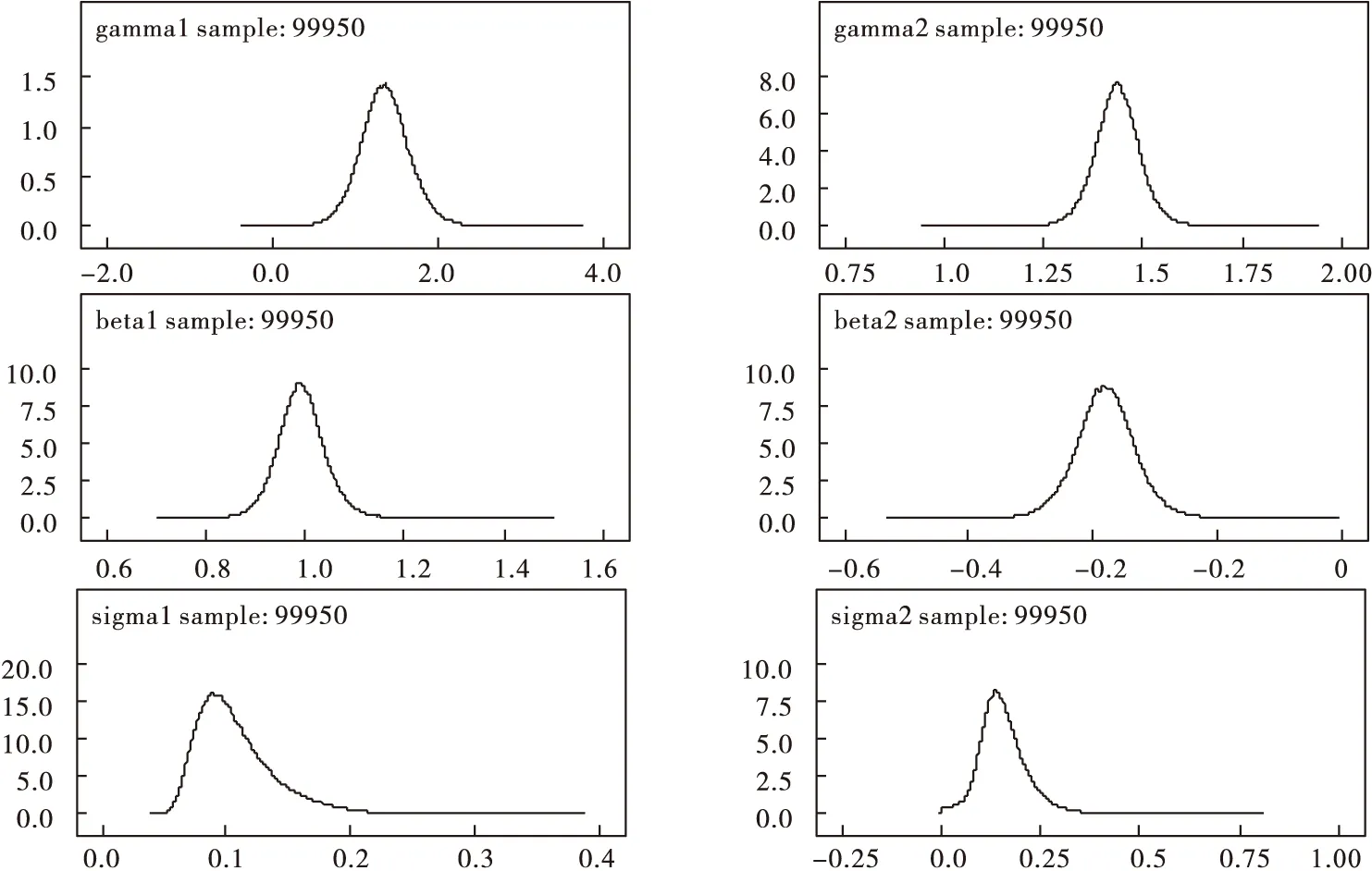
图5 迭代10万次核密度函数图
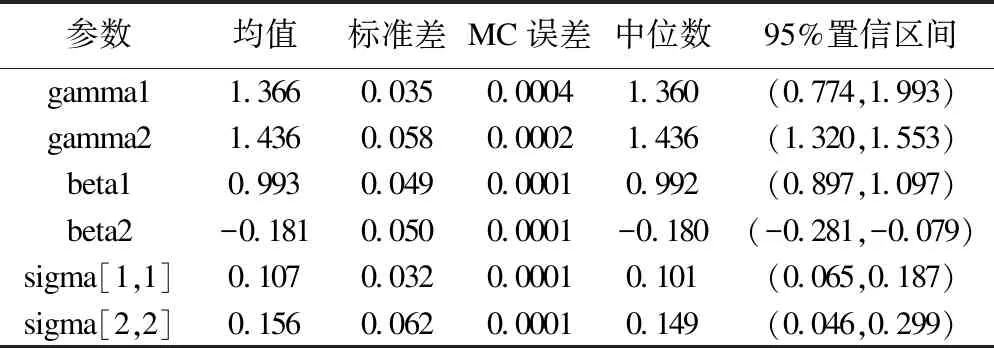
参数均值标准差MC误差中位数95%置信区间gamma113660035000041360(0774,1993)gamma214360058000021436(1320,1553)beta109930049000010992(0897,1097)beta2-0181005000001-0180(-0281,-0079)sigma[1,1]01070032000010101(0065,0187)sigma[2,2]01560062000010149(0046,0299)
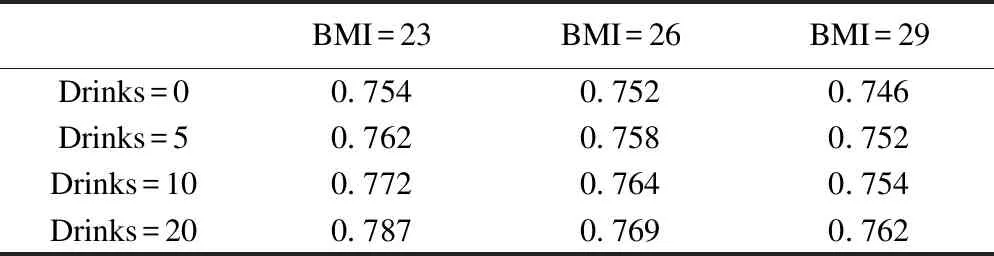
表6 不同肥胖程度,不同酗酒量下AUC
小 结
本文主要探讨了针对重复诊断数据的ROC曲线广义线性混合效应模型的原理及其参数估计方法,并结合医学实例,阐释了该模型的软件实现与应用。重复测量诊断数据是医药卫生研究中常见的数据形式,诊断试验的准确度评价也是医学研究不可或缺的部分。本文介绍的ROC曲线广义线性混合效应模型,是一种考虑协变量层次效应对诊断试验准确度影响的直接回归模型,同时还度量了重复测量诊断数据间的相关性,建立了带有随机效应的回归模型。利用诊断准确度的综合指标(ROC曲线下面积),对协变量影响和随机效应影响下的诊断试验准确度进行合理评价,综合性强,准确性高。在实际应用中,该方法建模灵活,解释合理,通过WinBUGS软件编程可方便实现,不仅可以用于诊断试验结果为连续性的重复测量数据和有序多分类的重复测量数据的分析,而且对于诊断试验结果的分布不作特定要求,根据协变量和随机效应对诊断试验准确度综合指标的影响,绘制不同条件下的ROC曲线并计算其曲线下面积,从而形象直观地评价诊断试验的准确度,为临床决策提供理论依据。
[1]李康,魏韦.医学诊断试验评价的ROC分析——重复测量诊断数据的ROC曲线.中国医院统计,2001,8(1):3-6.
[2]Zhou XH著.宇传华译.诊断医学统计学.北京:人民卫生出版社,2005.
[3]尉洁,宋娇娇,刘桂芬.基于贝叶斯估计的诊断试验ROC曲线回归模型.中国卫生统计,2010,27(2):152-154.
[4]Zhao Y,Staudenmayer J,Coull BA,et al.General Design Bayesian Generalized Linear Mixed Models.Statistical Science,2006,21(1):35-51.
[5]O′Malley AJ,Zou KH.Bayesian multivariate hierarchical transformation models for ROC analysis.Stat Med,2006,25(3):459-479.
(责任编辑:刘 壮)
ROC Curve Based on Generalized Linear Mixed Effects Models in Repeated Diagnostic Tests
Ma Chuntao,Xiong Wei,Tian Maozai
(CenterofStatistics,theSchoolofStatistics,RenminUniversityofChina(100872),Beijing)
Objective To investigate the impact of covariates on diagnostic test and assess the correlation between repeated measurement data,this paper explores innovative modeling techniques of ROC curve.Methods We introduce the new ROC curve method based on generalized linear mixed effects model and apply Bayesian techniques to parameters estimation with Winbugs Software.Further,areas under the ROC curve(AUC) with different values of covariates could be calculated in terms of assessment.Results Cases analysis results indicate the proposed method efficiently explores the repeated measurement data and provides parameters with practical significance,serving as a golden reference.Conclusion The ROC curve based on generalized linear mixed effects models can be effectively used to solve the test accuracy evaluation problem of the repeated diagnostic trials.
ROC curve;Mixed effects;Bayesian;Repeated measurement;Diagnostic tests
*:教育部哲学社会科学研究重大课题攻关项目(No.15JZD015),国家自然科学基金(No.11271368),北京市社会科学基金重大项目(No.15ZDA17),教育部高等学校博士学科点专项科研基金(No.20130004110007),国家社会科学基金重点项目(No.13AZD064),教育部人文社会科学重点研究基地重大项目(15JJD910001),北京市社科联项目决策咨询项目(No.2016010021),中国人民大学科学研究基金(中央高校基本科研业务费专项资金资助)项目成果(No.15XNL008)
1.中国人民大学应用统计科学研究中心,中国人民大学统计学院(100872)
2.对外经济贸易大学大数据与风险管理研究中心,统计学院
3.兰州财经大学统计学院
4.新疆财经大学统计与信息学院
△通信作者: 田茂再,E-mail:mztian@ruc.edu.cn
