基于不同类型小区的开放效果分析
2017-03-09龚长会管怡成颜廷晓
龚长会+管怡成+颜廷晓
摘要:为研究小区与周边道路结构对小区开放的影响,文章首先依据小区结构为方格网形和环形,周边道路为T形和十字形构建了4种不同类型的小区,在此基础上选取不同时间段的车流量的大小,分别求解四种不同类型的小区在不同车流量大小下的道路通行能力,根据交通仿真软件对结果进行仿真,发现:方格网形结构的小区开放有利于周边道路的车辆通行,环形结构小区的开放作用相反;车流量大的时候开放小区比车流量小的时候开放小区效果更好;周边道路结构对于周边道路通行情况的影响不明显。
关键词:小区;开放效果
在考虑不同类型小区的开放效果时我们选取小区出入口处130米的城市道路为研究目标,首先根据小区的两种结构和周边道路的两种结构构建4种不同类型的小区,然后应用所建模型针对早、中、晚不同的车流量逐一分析这四种小区开放后的效果,最后使用交通仿真软件对这四种小区开放前后的效果进行仿真,结合模型求解结果和仿真结果来定量分析各类型小区开放前后对道路通行的影响。
一、小区的构建
构建小区需要将小区的结构和周边道路的结构进行组合,首先分别给出小区和周边道路的结构图,如图1-4所示。
(一)小区结构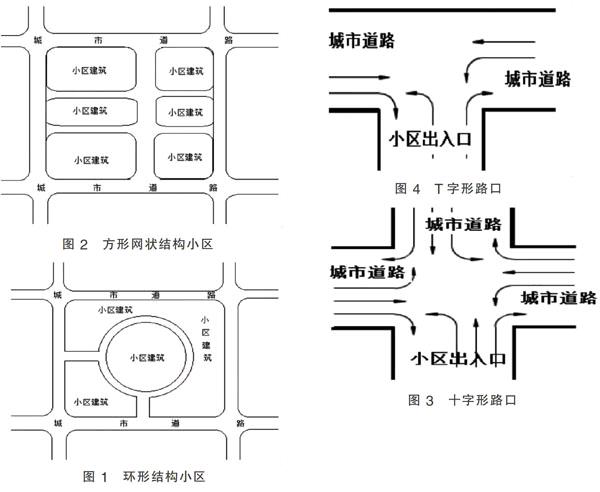
小區结构的不同主要体现在小区内部道路结构的不同,内部道路结构主要分为两种,即环形和方形网状形结构,如下图所示,环形结构和方形网状结构的小区内部道路不同,因此这两种不同道路结构的小区开放后对周边道路会产生不同的影响,需要分别予以讨论。
(二)周边道路结构
小区周边道路结构主要体现在小区的出入口与外界道路连接的路口类型,即是十字形路口还是T字形路口,具体如下图所示:
在得到了小区和周边道路的结构之后,对其进行组合得到4种不同类型的小区,即:①内部环形,外部十字形;②内部环形,外部T字形;③内部网状,外部十字形;④内部网状,外部T字形。
(三)道路通行能力的计算
考虑到车辆在环形道路和直线型道路的通行能力的计算方式不同,十字路口和T字形路口中各车道的通行能力的计算方式也不同,于是对于这些情况需要分别给出公式。
1. 环形交叉口的通行能力公式
对于圆环形小区的外部道路,其实际道路通行能力的计算与常见的直线型道路计算方式不同,以常规环形交叉口为例,采用在环形交叉口中应用较为广泛的沃尔卓普公式来分析圆环形小区的外部道路与其他道路的交叉口通行能力。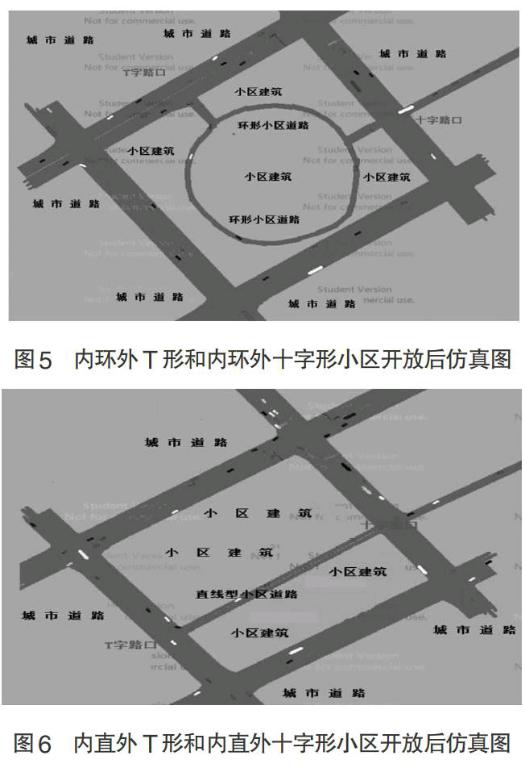
其中:Qm是该环形交叉口的最大道路通行能力;Y是交织段宽度;E是环交入口引道平均宽度;J是交织段内进行交织的车辆与全部车辆之比;g是交织道长度。
2. 直道交叉口的通行能力公式
①对于专用直行车道
其中:Qd是该直道交叉口的实际通行能力;tz是一个信号灯周期时长;tx是一个信号灯周期内的绿灯时长;tm是一个信号灯周期内的绿灯损失时间;tp是前后两车通过停车线的平均间隔时间。
②对于专用左行车道
其中:Ql是该专用左行车道交叉口实际通行能力;t是一个信号灯周期时长;nl是一个信号灯周期内允许左行的车辆数。
③对于专用右行车道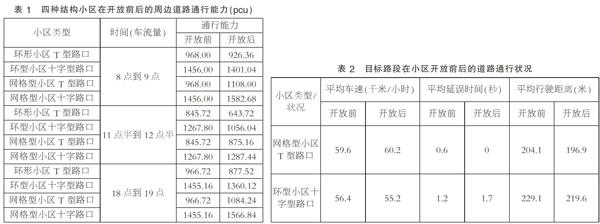
其中:Qr是该专用右行车道交叉口实际通行能力;t是前后两辆右行车通过停车线的平均间隔时间。
④对于单车道直行左行混杂车道
因为单一车道有两个方向,所以两者往往会相互干扰造成拥堵。因此必须对单车道直行左行混杂车道设定干扰系数KL,公式如下:
Qdl=Qd(1-pt)KL
其中:Qdl是单车道直行左行混杂车道实际通行能力;pt是左行车在该车道所占比例;KL是干扰系数,一般取。
⑤对于单车道直行右行混杂车道
原理与单车道直行左行混杂车道相似,但是其参数干扰系数KR一般取值为,其公式如下:
Qdr=Qd(1-)KR
对于多车道交叉口,其实际通行能力是左转车流、右转车流与直流车流三者的总和。
三、环形和直道交叉口的通行能力
分别选取早晨(8:00-9:00)、中午(11:30-12:30)、及晚上(18:00-19:00)的环形、直道交叉口的通行能力参数的均值代入相应的道路通行能力计算公式中,得到四种结构的小区周边道路在小区开放前后早晨的通行能力结果,如表1所示。
四、软件仿真
在计算出四种小区结构在不同车流量下的道路通行能力后,我们使用交通仿真软件对我们的计算结果进行仿真检验,这里给出四种小区在开放后的仿真图,如图所示:
为了使仿真的结果更贴合实际情况,在使用软件进行仿真时,我们将小区内部的车道设置为单车道,小区周边的道路设置为三车道,在小区周边的道路交叉口和小区的出入口设置了红绿灯,并加入多种车型进行模拟。选取小区出入口处130米长的周边道路为研究路段,仿真出在10分钟内目标路段的在不同交通流量下的道路通行情况,如表2所示。
分析表2的仿真结果发现网格型小区T型路口在小区开放后相比开放前的平均车速得到了提高,平均延误时间得到了减少,平均行驶距离得到了降低;而环型小区十字型路口在小区开放后相比开放前的平均车速变慢,平均延误时间变高,平均行驶距离变大。
于是根据仿真结果我们可以看出在一定车流量下,网格型小区的开放对其T型出入口周边道路的交通情况有积极的影响,而环型小区的开放对其十字型出入口周边道路的交通情况具有不利的影响,仿真结果与计算结果相符。
五、结果分析
横向分析表1可知,在小区内部结构为环形时,无论在什么时段(车流量)的情况下,小区开放后周边道路通行的通行能力都不如开放前,说明环形内部结构的小区无论在什么样的周边道路结构和车流量的情况下都不适合开放。
当小区内部结构为网格型时,无论在什么样的周边道路结构和车流量的情况下,小区开放后周边道路通行的通行能力都比开放前好,说明网格型的小区适合对外开放。
而在分析周边道路结构对小区开放效果影响时,需控制小区结构和车流量不变。分析表1数据发现周边道路结构对小区开放效果的影响有好有坏即无法确定,因此认为周边道路类型对小区开放没有大的影响。
在纵向分析表1时,发现在中午车流量较小时开放小区对周边道路的积极影响最小,而在早晨和晚上车流量较大时开放小区对周边道路的积极影响最大。说明车流量大的小区开放后对于周边道路的交通的改善效果要大于车流量小的小区开放后对周边道路的交通的改善效果。
参考文献:
李冬梅.李文权.道路通行能力的计算方法[J].河南大学学报,2002(02).
(作者单位:南京邮电大学贝尔英才学院)
