基于静态法高速列车抗横风倾覆影响因素研究*
2017-03-07罗禄林楚琦星贾永兴梅元贵
罗禄林 楚琦星 贾永兴 牛 军 梅元贵
(兰州交通大学机电工程学院,730070,兰州∥第一作者,硕士研究生)
基于静态法高速列车抗横风倾覆影响因素研究*
罗禄林 楚琦星 贾永兴 牛 军 梅元贵
(兰州交通大学机电工程学院,730070,兰州∥第一作者,硕士研究生)
随着我国高速铁路的飞速发展,风区运营的高速铁路不断出现,需对高速列车的抗横风倾覆性能进行深入研究。在对比分析日本的国枝方法和日比野有方法的基础上,针对我国CRH5H型动车组建立了横风倾覆静态计算模型,并对车体自重、转向架一系及二系悬挂刚度对列车抗倾覆性能的影响进行了数值模拟。数值计算结果符合实际规律,计算模型和方法可为风区运营车辆抗倾覆安全设计提供参考。
高速列车; 倾覆稳定性; 静态方法
Author′s address School of Mechanical and Electrical Engineering, Lanzhou JiaoTong University,730070,Lanzhou,China
随着我国高速铁路的不断发展,风区运营线路不断出现。我国幅员辽阔,各地区风场环境差异巨大。气象统计结果表明,京沪高铁沿线各站20 m/s级别日极大风速的发生概率为81%~100%,百年一遇日极大风速达到38 m/s[1]。京津城际铁路沿线春冬季瞬时最大风速可达31.6 m/s[2]。目前已建成运营的兰州至乌鲁木齐第二双线全长1 776 km,其中近580 km线路在风区运行。兰新高铁沿线通过新疆境内的百里风区、三十里风区、烟墩风区、达坂城风区和甘肃境内的安西风区,其中百里风区大于8级风的大风天数超过百天,风速最高可达64 m/s[3-4]。大风多次引起既有兰新铁路中断行车,甚至列车脱线、翻车等重大事故[5],给铁路运输造成巨大损失。强风给风区运行高速列车带来了极大的安全隐患,因此有必要对高速列车横风环境安全运行性能进行研究。
文献[6]采用静态方法给出了列车在横风作用下的倾覆系数计算公式,即国枝式。文献[7-8]改进了国枝式,考虑了转向架中更多悬挂部件的影响。文献[9]建立了车辆倾覆的静态模型,对普速列车大风环境下倾覆特性进行了研究。静态法建模快速简单,对计算工具的要求低。
文献[10-12]运用多体动力学仿真商业软件研究了大风作用下列车的倾覆性能。多体动力学仿真商业软件能够对影响车辆倾覆的各部件进行多自由度数值模拟,但其建模过程复杂,资源耗费大。文献[13]使用准静态方法得到了与多体动力学仿真商业软件结果媲美的计算结果,其建模过程相比静态方法同样较为复杂。
本文针对我国兰新高铁第二双线运营的CRH5H型动车组,建立了基于KUNIEDA[6]和YU HIBINO[7-8]的两种横风倾覆静态计算模型,并对影响列车倾覆的多种参数进行研究,以期为我国风区运营高速列车抗倾覆安全设计提供参考。
1 数学模型
CRH5H高寒抗风沙动车组为满足长期在8级至12级强风沙环境运行设计[14]。其机械材料、密封橡胶、油脂以及电气元件等在前期设计中充分考虑了低温适应性能,并特别针对大风安全倾覆及侧窗玻璃抗砾石冲击安全等进行计算或试验验证。为提高抗倾覆性能,CRH5H动车组转向架设置了抗侧滚扭杆。
车辆倾覆一般可分为三种情况:①曲线外侧倾覆,当车辆位于曲线轨道上运行时,在最不利外力组合作用下,向曲线轨道外侧发生倾覆;②曲线内侧倾覆,当车辆以较低速度行驶于曲线轨道上时,由于曲线轨道有外超高,使得列车向内倾,同时受到向内侧力(风力、振动惯性力)作用,使得车辆向曲线内侧倾覆;③平直轨道倾覆,车辆在直线轨道上运行,受到大风作用或者同时遭受由于线路不平顺等原因造成的车辆横向剧烈振动的横向惯性力的作用而引起车辆向一侧倾覆。本文建模过程中考虑曲线外侧倾覆,且以半车模型建模。在不考虑超高时,计算模型可用于直线轨道倾覆的计算。
车辆抗倾覆性能可用车辆迎风侧车轮减载程度来衡量,即倾覆系数[15]。
(1)
式中:
Q0——静态轮重;
ΔQ——迎风侧轮重减少量;
P1——迎风侧轮轨间垂向作用力;
P2——背风侧轮轨间垂向作用力。
1.1 国枝方法
车辆位于弯道上时受到的外力如图 1所示。受力分析时主要考虑:①车辆通过曲线时未被平衡的离心力,其中包括车辆通过曲线时的离心力与外轨超高引起的重力在离心力方向上的分力;②车辆横向振动惯性力;③横风作用在车辆上产生的横向气动力、气动升力。
推导车辆倾覆系数公式时,国枝方法假设:
(1) 不考虑由于车体倾斜造成的各侧向力的作用点距离轨面的垂直高度的变化;
(2) 不考虑车辆簧下部分所受气动力的影响;
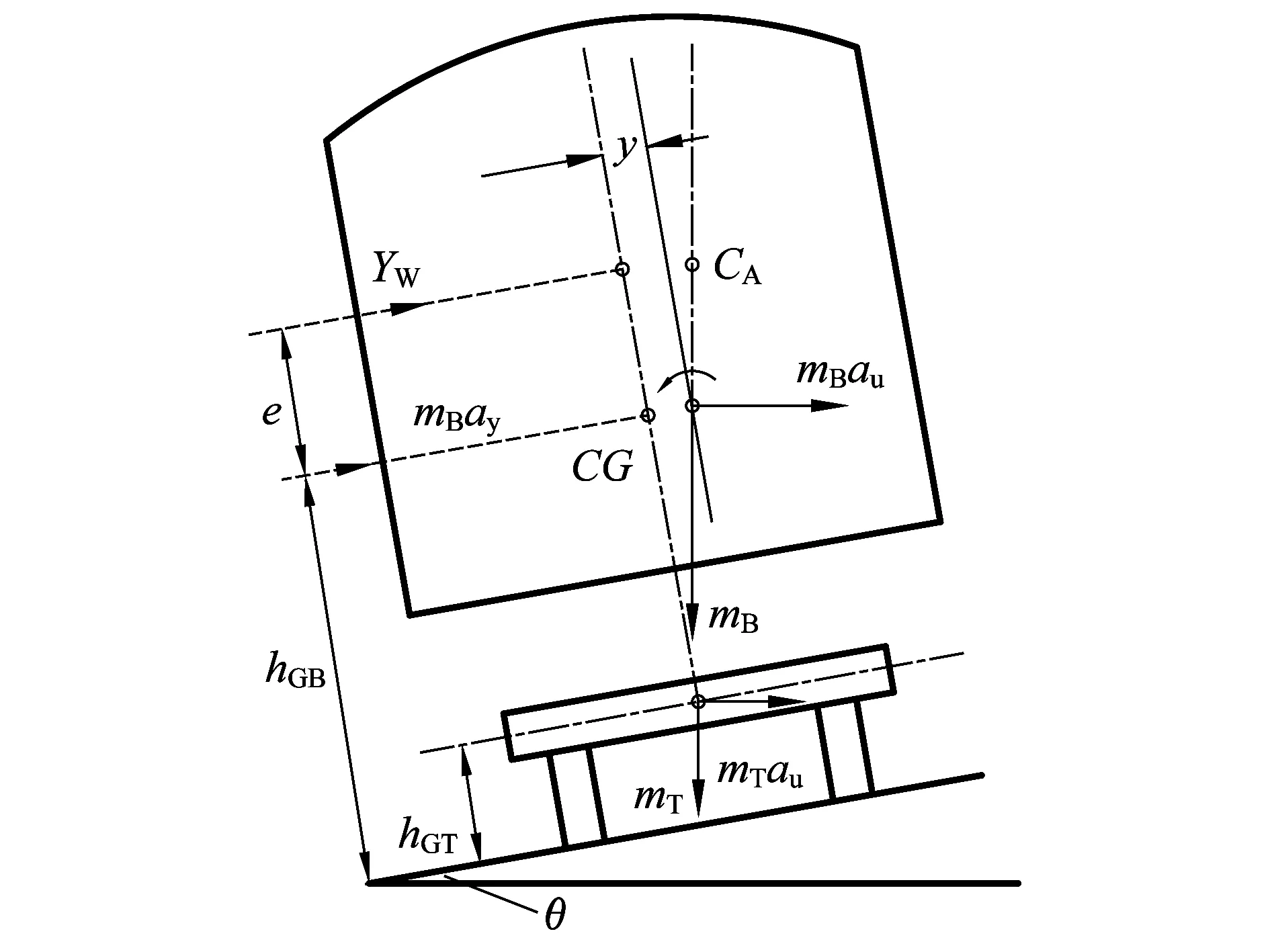
图1 车辆过曲线时的受力状态
(3) 不考虑车辆簧上质量垂直振动惯性力的影响;
(4) 不考虑车辆簧下质量垂向和横向振动惯性力的影响,并假定簧下质量的重心位于轮对中心;
(5) 由于高速铁路曲线半径相对于车体长度较大,车钩力方向偏移车钩中心线方向较小,因此不考虑车钩力。
(6) 不考虑轮对踏面在轨面上的滑移;
(7) 将横风引起的横向力集中于风压中心。
根据静态力矩平衡原理,列车倾覆系数可表示为:
(2)
式中:
μ——转向架质量mT与半车体质量mB之比;
v——车速;
R——线路曲线半径;
c——轨道外超高;
YW——气动力;
hGB——车体重心距轨面高度;
hBC——风压中心距轨面高度;
hGT——转向架重心距轨面高度;
G——轮轨接触点横向跨距;
g——重力加速度;
e——风压中心至车体重心间的距离;
cy——单位横向力引起的车体重心横向位移,cy=1/(2Ky),其中Ky为每个转向架弹簧的横向刚度;

图1中,车体重心横向位移y=cyY+cyφM,其中Y为横向力,M为侧滚力矩。
1.2 日比野有静态方法
日比野有[7]在国枝公式基础上,考虑车体重心在两级悬挂作用下的横向位移和侧滚角位移,建立了日比野有静态方法(以下简为“静态方法”)。静态方法与国枝方法的不同点在于:
(1) 更多地考虑了转向架的弹性元件的影响;
(2) 对于外力引起的车体重心位移的变化,除了考虑横向位移变化之外,还考虑了绕重心的侧滚位移。
车辆位于曲线轨道上时受力模型如图2所示。对背风侧轮轨接触点取矩,有:
hGTmTau-hGB(mBau+mBay)-hBCFS
(3)
式中:
FS——横向力;
FL——气动升力;
mB——半车体质量;
ay——车体横向振动加速度;
au——超离心加速度;
hBC——风压中心距轨面高度;
hGB——车体重心距轨面高度;
yB——车体重心横向位移;
ΦB——车体侧滚角位移。
由式(3)可得计算倾覆系数计算公式:
(4)
式(4)中,yB、ΦB与FB(FB=FS+mBau+mBay)和绕车体重心的侧滚力矩MB(MB=-eFB)之间的关系可按以下线性关系式定义:

图2 日比野有车辆倾覆模型
yB≡CyFB+DyMB+yB0
ΦB≡CΦFB+DΦMB+ΦB0
(5)
式中:
Cy——每单位横向力的重心横向位移;
Dy——每单位力矩的重心横向位移;
CΦ——每单位横向力的重心侧滚位移;
DΦ——每单位力矩的重心侧滚位移;
yB0,ΦB0——止挡影响项。
Cy、Dy、CΦ、DΦ为弹簧系统影响系数。
受到外力作用的车体在轴向弹簧附近产生侧滚角位移Φ1,在空气弹簧附近产生侧滚角位移Φ2,并在空气弹簧横向刚度作用下产生横向位移y2,这些位移相互叠加得到车体重心的横向位移yB、侧滚角位移ΦB及垂向位移zB,如式(6)所示。
(6)
式中:
h1——车体重心至轮轴中心的距离;
h2——车体重心至空气弹簧中心的距离。
车体在临界倾覆状态下,忽略车体重心各项位移储存的势能三次以上的项,同时考虑是否碰撞横向止挡和垂向止挡,根据虚功原理忽略二次以上无穷小项,可以得到车体重心的各项位移;将结果代入式(5)和式(6),便可得到式(4)中的yB和ΦB。
对于CRH5H高寒抗风沙动车组转向架,推导可得弹簧系统影响系数表达式为:
其中
hs=h1-h2-h3
式中:
h3——横向止挡中心到轮轴中心线的距离;
kys——横向止挡刚度;
ky——空气弹簧横向刚度;
k1——轴向弹簧垂向刚度;
k2——空气弹簧垂向刚度;
kr——抗侧滚扭杆刚度。
2 程序验证
根据推导得到的数学模型,采用Fortran语言编程,建立两种方法的计算程序。本文采用文献[6,8]提供的参数对程序的正确性进行验证。
2.1 国枝方法验证
图3为基于国枝方法编程计算得到的车速与临界倾覆风速之间的关系。已知车辆自重20 t,轮轨接触点中心跨距为1.5 m,其余参数详见文献[6]。从图3中可知,本文计算结果与文献计算结果完全吻合。

图3 车速和临界风速关系
2.2 日比野有方法验证
图4、图 5对比了基于日比野有方法计算得到的倾覆系数及车体重心横向位移与文献试验及计算的结果。计算所需车辆参数见表1[8]。
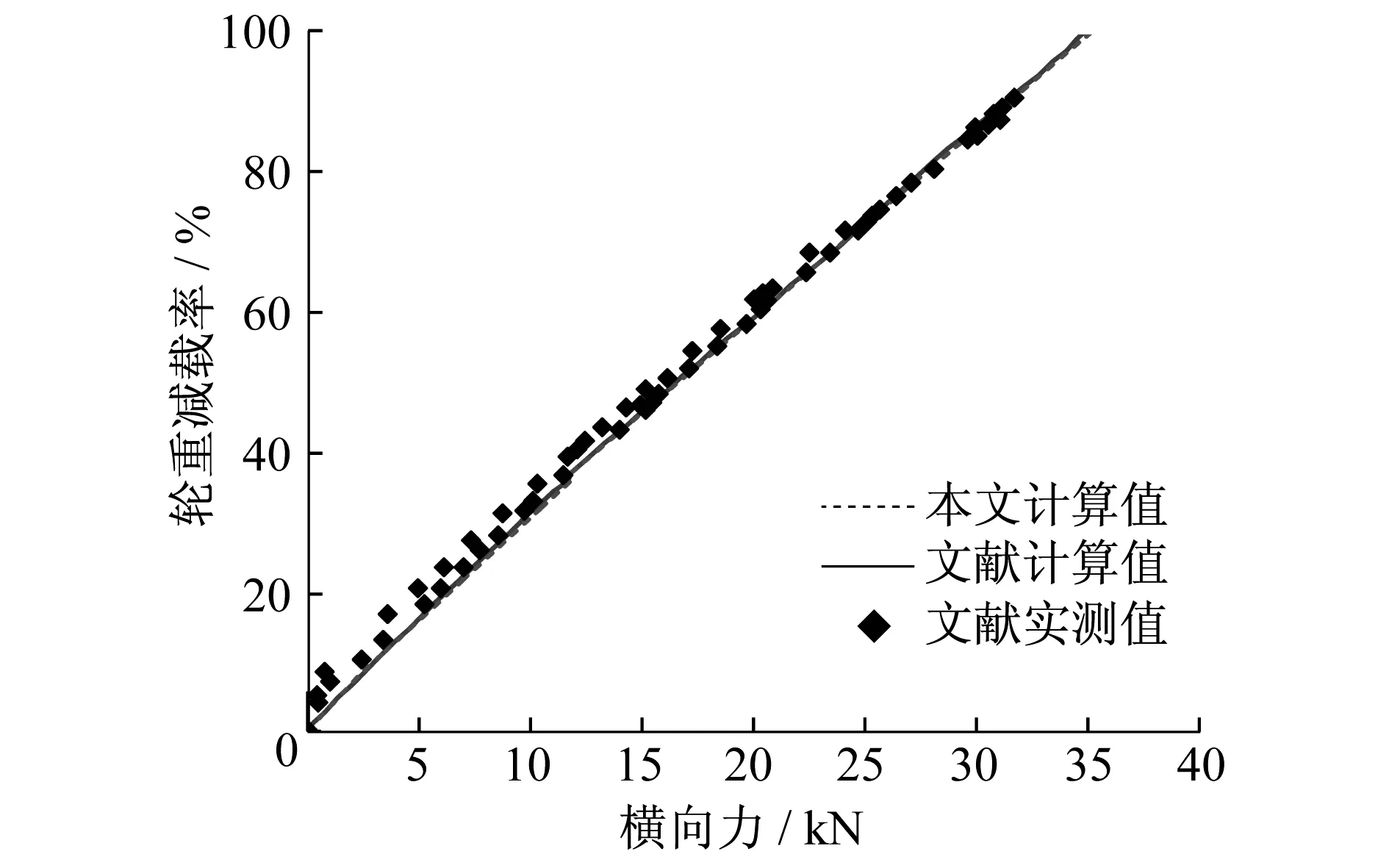
图4 横向力和倾覆系数关系
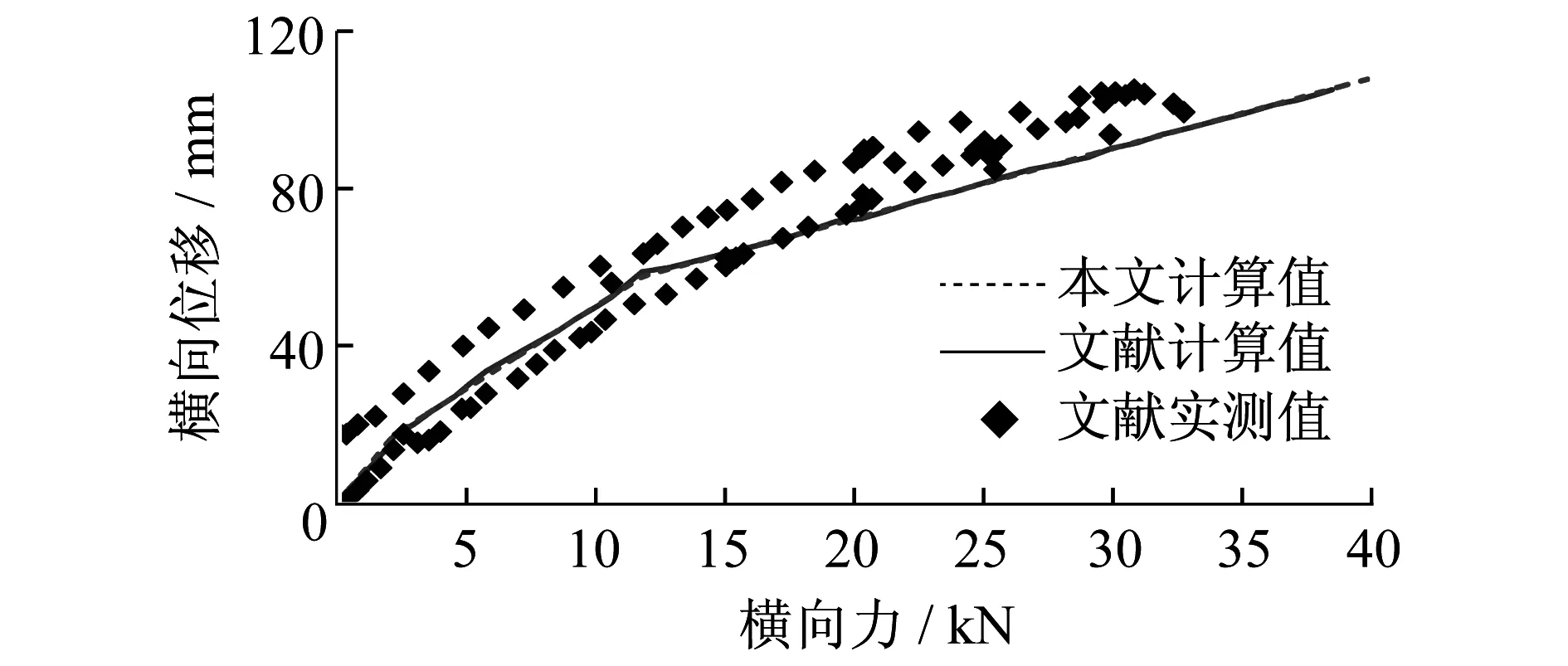
图5 横向力和横向位移关系

车辆参数参数值半车体质量mB/kg13365转向架质量mT/kg4492车体重心距轨面高度hGB/m1.5转向架重心距轨面高度hGT/m0.48车体中心距轨面高度hB1/m2.32车体距轨面高度hB2/m2.40车身侧面积之半SA/m224.96车轮半径rw/m0.43空气密度ρ/(kg·m3)1.205轮轨接触点横向跨距2b/m1.12轴箱弹簧横向跨距2b1/m1.64空气弹簧横向跨距2b2/m1.98空气弹簧中心距轨面高度hKC/m0.84横向止挡距轨面高度hSC/m0.505横向止挡间隙yS/m0.01
图4计算结果与文献[8]计算所得结果完全吻合,准确反映了试验结果。图 5计算结果与文献计算结果完全吻合。文献[8]分析了造成计算结果与试验结果差异变大的原因在于车体侧滚时先后碰到横向止挡和垂向止挡后,车体重心的实际位移和计算的位移不一致。
2.3 国枝方法和日比野有方法对比
当横向力线性增大时,分别以上述两种方法计算车辆倾覆系数,结果如图 6所示。可以看到,相同的横向力作用下,国枝方法计算所得倾覆系数小于日比野有方法。该结论与国外试验结果相同[16]。造成这种结果的原因在于:①国枝方法没有考虑气动升力;②国枝方法只考虑了横向和垂向刚度对车辆倾覆的影响,但没有考虑互相的影响;③该方法没有考虑止挡对车辆倾覆的影响。
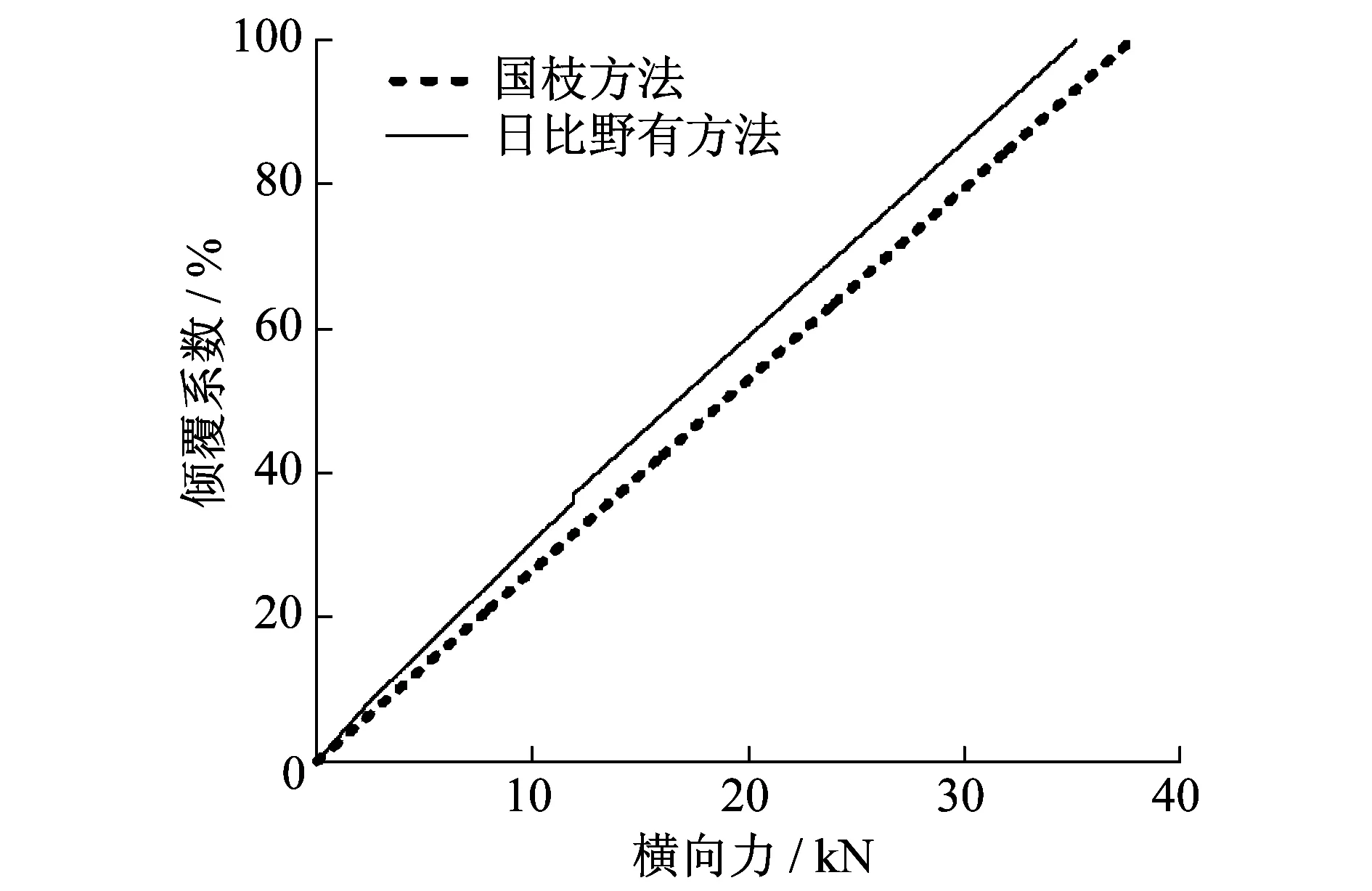
图6 横向力和倾覆系数的关系
3 影响车辆倾覆系数的因素分析
对影响车辆倾覆的多个因素进行数值模拟。
3.1 车体自重对倾覆系数的影响
从已掌握的资料看,高速列车的车体自重范围在26~52 t之间。改变车体自重,计算其倾覆系数。倾覆系数与车体自重变化的关系如图7所示。其中,横坐标为CRH2车体自重与CRH5H车体自重的比值。参考研究团队针对兰新高铁第二双线进行的CFD(Computational Fluid Dynamics)数值模拟结果及其他文献,列车以250 km/h通过风区时受到的横向力在25 kN左右。

图7 车体自重对倾覆系数的影响
由图7可知,相同的横向力作用下,随车体自重的增大,倾覆系数逐渐变小,横风下安全性增强。这与一般的认识相同。可见,在目前车体轻量化趋势下,需从车体悬挂刚度及减小横向力等方面入手,减小轻量化车体引起的抗倾覆性能恶化的趋势。
3.2 悬挂刚度对倾覆系数的影响
图8所示为抗侧滚扭杆刚度、一系悬挂刚度及二系悬挂刚度与倾覆系数的关系。其中横坐标为计算时CRH2各悬挂部件刚度与CRH5H各部件刚度的比值。可以看到,随抗侧滚扭杆、一系悬挂刚度及二系悬挂刚度的增加,倾覆系数均有减小的趋势。其中抗侧滚扭杆刚度与一系悬挂刚度变化对倾覆系数的影响比二系悬挂刚度变化的影响显著。
图9所示为横向止档刚度对倾覆系数的影响。可见,随着横向止档刚度的增大,车辆的抗倾覆性有所提升。

图8 悬挂部件刚度对倾覆系数的影响

图9 横向止档刚度对倾覆系数的影响
4 结语
国枝方法和日比野有方法都是以静态力矩平衡为基础原理,其建模容易,计算时间短。日比野有方法是在国枝方法的基础上进行修正而来。本文运用静态方法建立了CRH5H动车组倾覆模型,在验证程序合理性的基础上,研究了车体自重、抗侧滚扭杆刚度、一系和二系悬挂刚度以及横向止档刚度对倾覆系数的影响,数值计算结果符合实际规律。结果表明,车辆自重和车体所受横向力是影响列车倾覆的最主要因素。由于受到其它如轴重、车体机械强度等方面的制约,需要在高速列车轻量化与倾覆安全性之间找到一个平衡点。通过加设挡风墙等设法降低车体横向力是目前保证风区列车运营安全的主要方法。调节悬挂系统各部件的刚度对提高列车倾覆安全有一定作用,但数值计算分析发现,其对倾覆系数的影响相比车体自重和横向力的影响要小。
[1] 张强,杨贤为,张永山,等.京沪沿线强降水频率及大风频率分布特征[J].气象科技, 2003,31(1):45-49.
[2] 马淑红,马志福.瞬时最大风速对京津城际CRH3动车组行车安全影响[J].中国科技信息,2008(21):285-286.
[3] 李鲲.大风区高速铁路新型防风设施研究[J].中南大学学报(自然科学版),2012,43(2):756-762.
[4] 王争鸣.兰新高铁穿越大风区线路选线及防风措施设计[J].铁道工程学报,2015(1):1-6.
[5] 钱征宇.西北地区铁路大风灾害及其防治对策[J].中国铁路,2009(3):1-4.
[6] KUNIEDA M.Theoretical Study on the Mechanics of Overturn of Railway Rolling stock[J].Railway Technical Research Report,1972(793):1-15.
[7] ISHIDA Y H H.Static analysis on railway vehicle overturning under vrosswind[J].Railway Technical Research Report,2003,17(4):39-45.
[8] HIBINO Y,Shimomura T,Tanifuji K.Verification of Static Analysis on Railway Vehicle Overturning under Crosswind[J].Transactions of the Japan Society of Mechanical Engineers C,2009,75(758):2605-2612.
[9] 高广军.强侧风作用下列车运行安全性研究[D]. 长沙:中南大学,2008.
[10] THOMAS D,DIEDRCHS B,Berg M,et al.Dynamics of a High-speed Rail Vehicle Negotiating Curves at Unsteady Crosswind[C]∥Proceedings of the Institution of Mechanical Engineers.London:SAGE Publications Ltd.,2010:567-579.
[11] TAKAHIRO HOSOI K T.Effect of Crosswind on Derailment of Railway Vehicles Running on Curved Track at Low Speed[J].International Journal of Railway,2012,5(2):93-101.
[12] 郗艳红.横风作用下的高速列车气动特性及运行安全性研究[D]. 北京:北京交通大学,2012.
[13] DIEDRICHS B,Ekequist M,Stichel S,et al.Quasi-static modelling of wheel-rail reactions due to crosswind effects for various types of high-speed rolling stock [C]∥Proceedings of the Institution of Mechanical Engineers.London:SAGE Publications Ltd.,2004:133-148.
[14] 王峰,张籍弟.浅谈高寒抗风沙动车组设计开发[J].山东工业技术,2015(1):56.
[15] 王福天.车辆动力学[M].北京:中国铁道出版社,1981.
[16] MORIYAMA A.Verification of railway vehicle overturning under crosswind by field data(an effect of the cross-sectional shape of vehicles)[J].Transactions of the Japan Society of Mechanical Engineers Series A,2012,78(791):2536-2548.
Influencing Factors on Overturning Resistance on High-speed Railway Vehicles against Crosswind Based on Static Method
LUO Lulin, CHU Qixing, JIA Yongxing, NIU Jun, MEI Yuangui
With the rapid development, more high-speed railways are constructed in strong wind regions, so the overturning resistance of railway vehicles against crosswind should be studied. Two different methods, KUNIEDA's method and Yu HIBINO's method are compared, which are used to evaluate the overturning stability of railway vehicles. An overturning resistance model is established based on the CRH5H EMU, the effect of different parameters, such as dead weight, bogie frame I and the hanging stiffness of bogie frame II against overturning is studied. The calculation results are in accordance with the order of nature. The numerical model and method can be used in the safety design of railway vehicle running in strong wind regions.
high-speed train; overturning stability; static method
*中国铁路总公司科研试验(Z2014-034);甘肃省高等学校基本科研业务费项目(214145)
U 271.91.1
10.16037/j.1007-869x.2017.01.005
2015-05-26)
